双余度永磁无刷直流电机绕组故障诊断研究

付朝阳, 刘景林, 张晓旭

(西北工业大学 自动化学院, 陕西 西安 710072)

在航空航天等高精密控制系统中，广泛采用余度控制技术。控制系统中实现余度控制一种方案是1台电机及其控制系统作为1个通道，采用多台电机及其控制系统并联运行，这种方案的缺点是体积大、重量重、成本高。另一种方案是将余度技术引入到电机上，电机定子中设置多套绕组，共用1套转子系统，每套绕组分别与控制系统构成独立的通道。该方案的特点是：体积小、重量轻、成本低。

目前，国内科研机构已对余度电机做了一些初步研究。文献[1]研究了双余度无刷直流电机的极弧系数对其转矩波动的影响，通过采用电磁场有限元分析的方法，计算了极弧系数对电气双余度波形和定位转矩的影响，给出了电气双余度极弧系数选取的参考方法。文献[2]采用场路结合的方法设计了一种用于直接驱动作动器(DDA)的电气/机械混合式四余度无刷直流力矩电动机，该电机具有同轴的2段定、转子，每段定子中隔槽嵌放2套绕组，从而构成电气/机械混合四余度，通过实验验证了该方案的可行性。文献[3]对双余度无刷电机的数学模型进行了推导，设计了相关原理样机，验证了双余度设计的可行性。文献[4]研究了绕组短路故障对直接驱动作动器(DDA) 用电气/ 机械混合四余度无刷直流力矩电动机(BLDCTM) 性能的影响，分析了短路故障对电机电气参数造成的影响，系统的仿真结果表明某一相绕组出现匝间短路或某余度的两相绕组出现相间短路时,系统依然可以正常运行，大大提高了系统的可靠性。

在上述文献中，大多针对双余度永磁无刷直流电机的设计及其控制方法进行了研究，针对故障诊断方面的研究较少。由于绕组中设置了2套绕组，大大提高了系统的可靠性，但是作为一个多源故障系统，双余度永磁无刷直流电机由于绕组间的耦合作用，存在一个故障对应多个故障特征和多个故障特征对应相似故障特征的情况，并且由于早期绕组故障信号微弱而难以被发现，给电机故障诊断带来了较大困难。

1 故障信号和小波函数的选择

双余度永磁无刷直流电机采用了2套电枢绕组，在电机运行时，2套绕组会通过电感互相耦合，

而当电机发生故障时，电机的转速、转矩和电流等都会发生变化，电机转矩方程如下所示：

T=CTφI

(1)

设电枢电流的脉动频率为fI，可知电机转速为

n=60fI/P

(2)

由上述2个公式可以看到，电机的转矩、转速均与电流相关。因此当电机发生故障时，电机的电枢电流信号会有比较明显的变化，主要表现在以下几个参数中：稳态电枢电流均值、稳态电枢电流的脉动幅度、稳态电流的脉动频率等。

信号的多分辨分析是信号的正交小波分解，其基本算法是Mallat提出的基于时间和尺度的二进分割快速算法，即著名的“Mallat塔形算法”，Mallat算法实现无冗余的正交分解。通过信号的正交小波分解，信号被分解到一系列频带上，且各频带互不相交。在确定的小波母函数和采样频率下，每个频带范围由尺度决定。电机发生故障时，每相电流波形包含不同的谐波成分，在不同的频带上谐波能量增强或抑制。因为不同类型的故障电流波形信号经小波分解后在各频带上的投影是不同的，所以故障信号在各频带投影序列的能量是故障类型的表现形式，因此可以把正交小波分解后每相电流空间信号能量作为特征向量，进行频带能量分析。

根据以上方法，对电机进行了动态仿真，在250 ms时，破坏控制电路为1相断路，选择Daubechies3和coif5分别对电流信号进行了2层小波分解，分别如图1和图2所示。

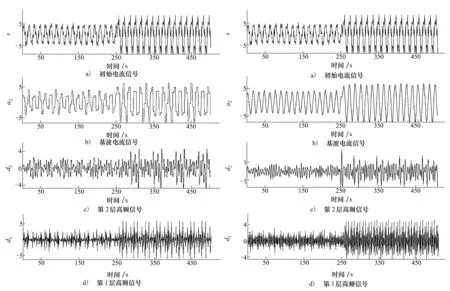
图1 Daubechies3小波分解图2 Coif5小波分解

由结果可知，在小波分解高频部分的第2层，250 ms时明显发生了突变信号，相比较而言，coif5小波函数更能反映出故障突变点，故本文选取coif5小波函数。

2 绕组开路故障分析及特征提取

绕组开路是电机的一种常见故障。对双余度高压永磁无刷直流电机来说，由于采用了2套电枢绕组，当其中1套发生开路故障时，另外1套仍然可以正常运行，不过相电流会变大。

以一余度C相开路为例，电机一余度A相和B相电流波形分别如图3和图4所示。

对每相电流信号进行2层多分辨率coif5分解，得到其中的d2分解系数。结果分别如图5和图6所示。

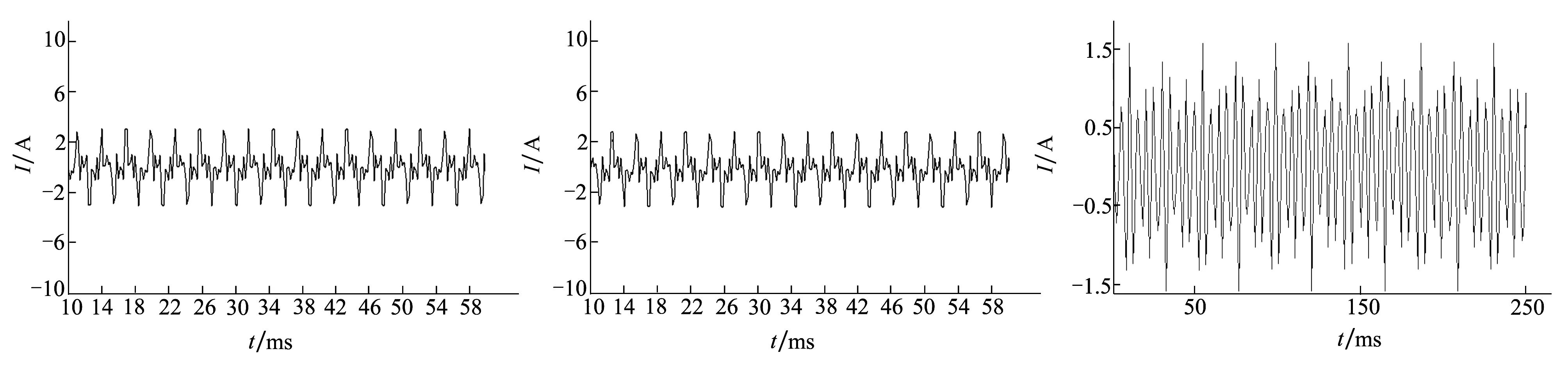
图3 一余度A相电流 图4 一余度B相电流 图5 A相电流d2分解系数

图6 B相电流d2分解系数

求每相d2层小波分解系数序列的能量，将其按照顺序排列，得到一个向量[213.91，213.91，0，260.57，257.54，55.55]，同样的方法我们可以得到其他相开路时特征向量，如表1所示。

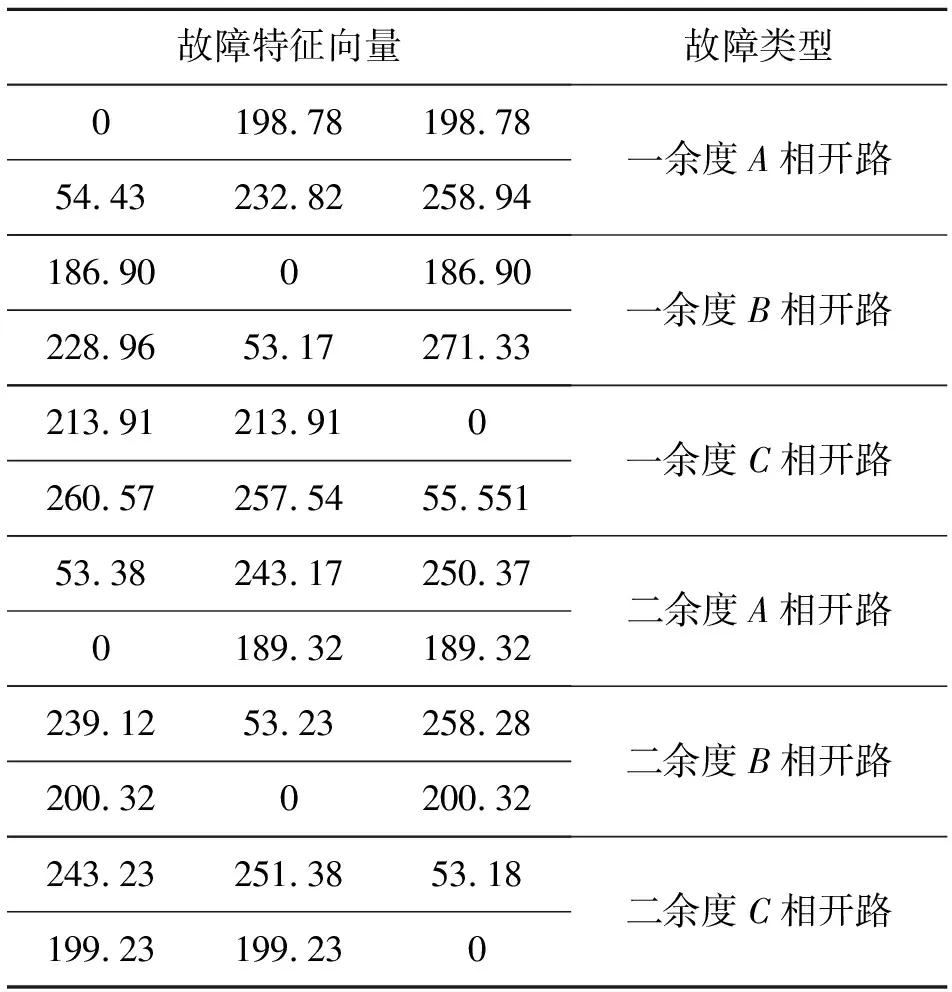
表1 故障特征向量表

3 匝间短路故障分析及特征提取

对于比较明显的多匝短路时，电流值会发生明显突变，而对于细微的匝间短路时，普通的电流检测则很难发现，为了能够准确地模拟短路故障，本文将其中的一个定子槽分为两部分，如图7所示(12点方向的定子槽被分为两部分)，这两部分分别嵌入线圈，保持总的匝数不变(与其他定子槽匝数一致)。

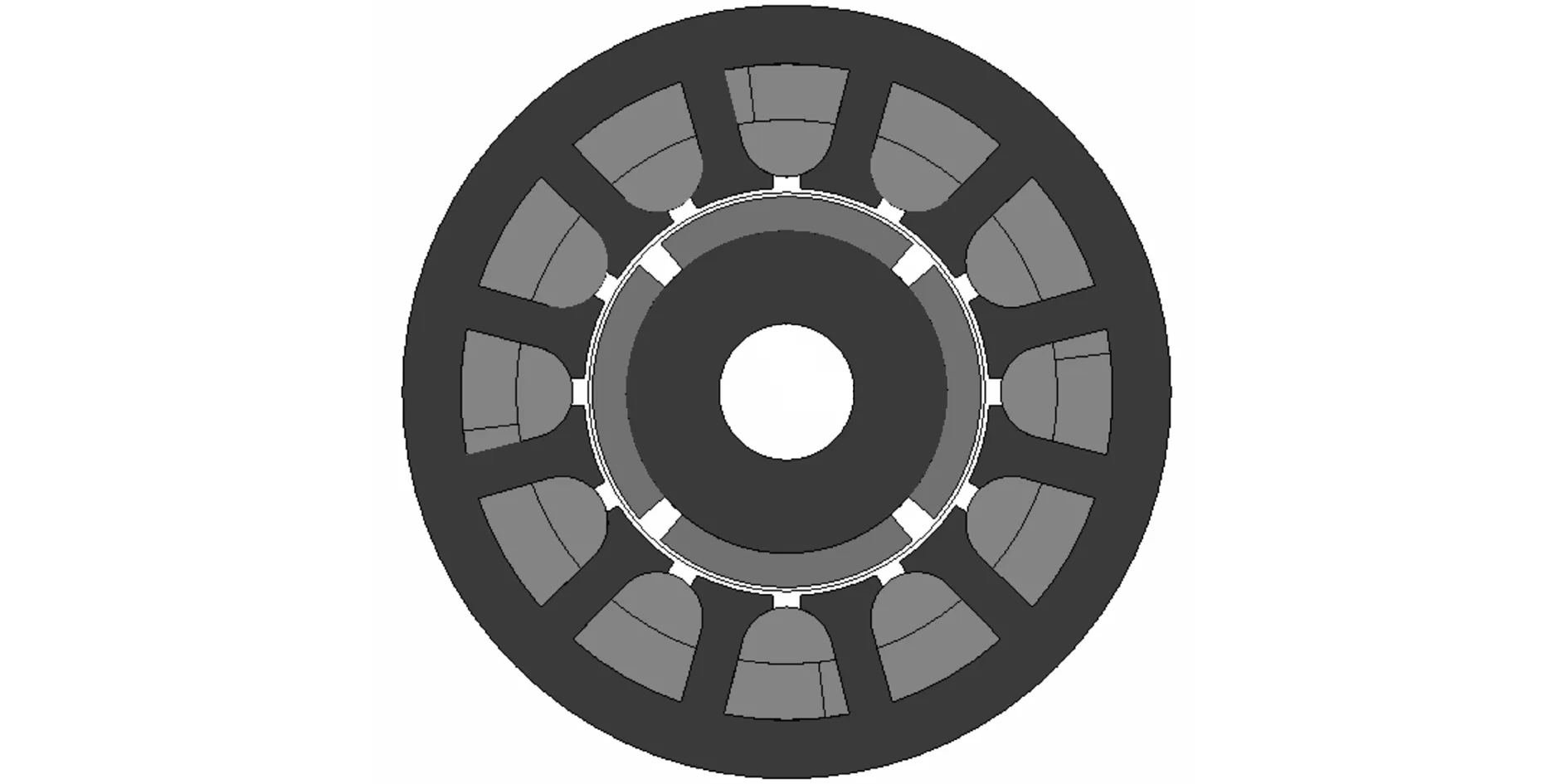
图7 匝间短路仿真模型

采用3D瞬态求解器进行计算，得到各相电流波形，如图3所示。与正常模型仿真相比，各相电流均略有增加，但不明显。

依据电机绕组开路时的计算方法，求每相d2层小波分解系数序列的能量，将其按照顺序排列，得到电机匝间短路时特征向量，如表2所示。

表2 故障特征向量表

4 故障模式识别

本文采用了小波分析与神经网络的松散型结合，选取小波作为信号处理的前置手段，为神经网络提供特征向量，之后完成训练和诊断。

为了便于分析，对输入样本进行归一化处理，对各故障状态能量值进行归一化后，结果如表3所示。

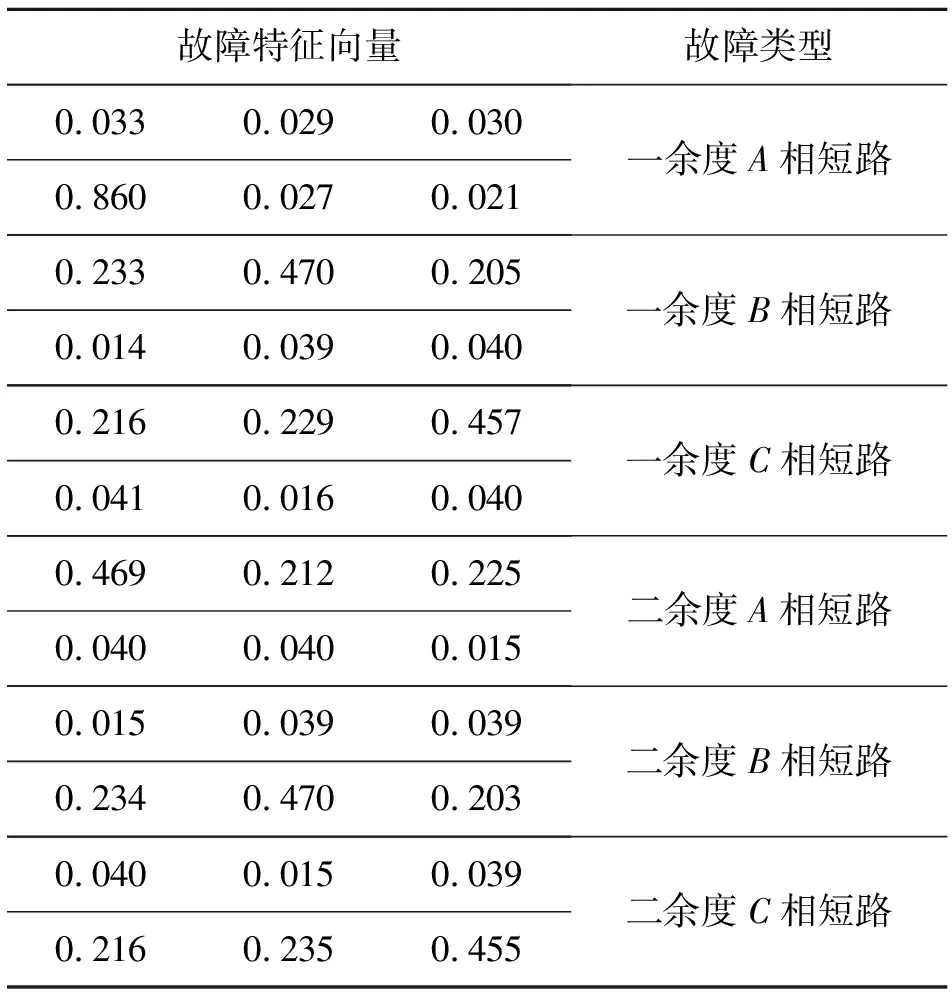
表3 归一化后的故障特征向量表

PNN是一种机构简单、训练简洁、应用相当广泛的人工神经网络。在实际应用中，尤其是在解决分类问题的应用中，它的优势在于用线性学习算法来完成以往非线性学习算法所做的工作。这种网络对应的权值就是模式样本的分布，因而能够满足实时处理的要求，本文采用PNN神经网络进行故障诊断。

在进行故障诊断的过程中，求和层对模式层中同一模式的输出求和，并乘以代价因子；决策层则选择求和层中最大输出对应的故障模式作为诊断结果。当故障样本的数量增加时，模式层的神经元将随之增加。而当故障模式多于2种时，则求和层神经元将增加。所以，随着故障经验知识的积累，概率神经网络可以不断横向扩展，故障诊断的能力也将不断提高。基于PNN的系统模型如图8所示。令网络的目标输出值为各故障状态对应的二进制代码，序号代表电机状态，1为正常，2为一余度A相短路，以此类推。

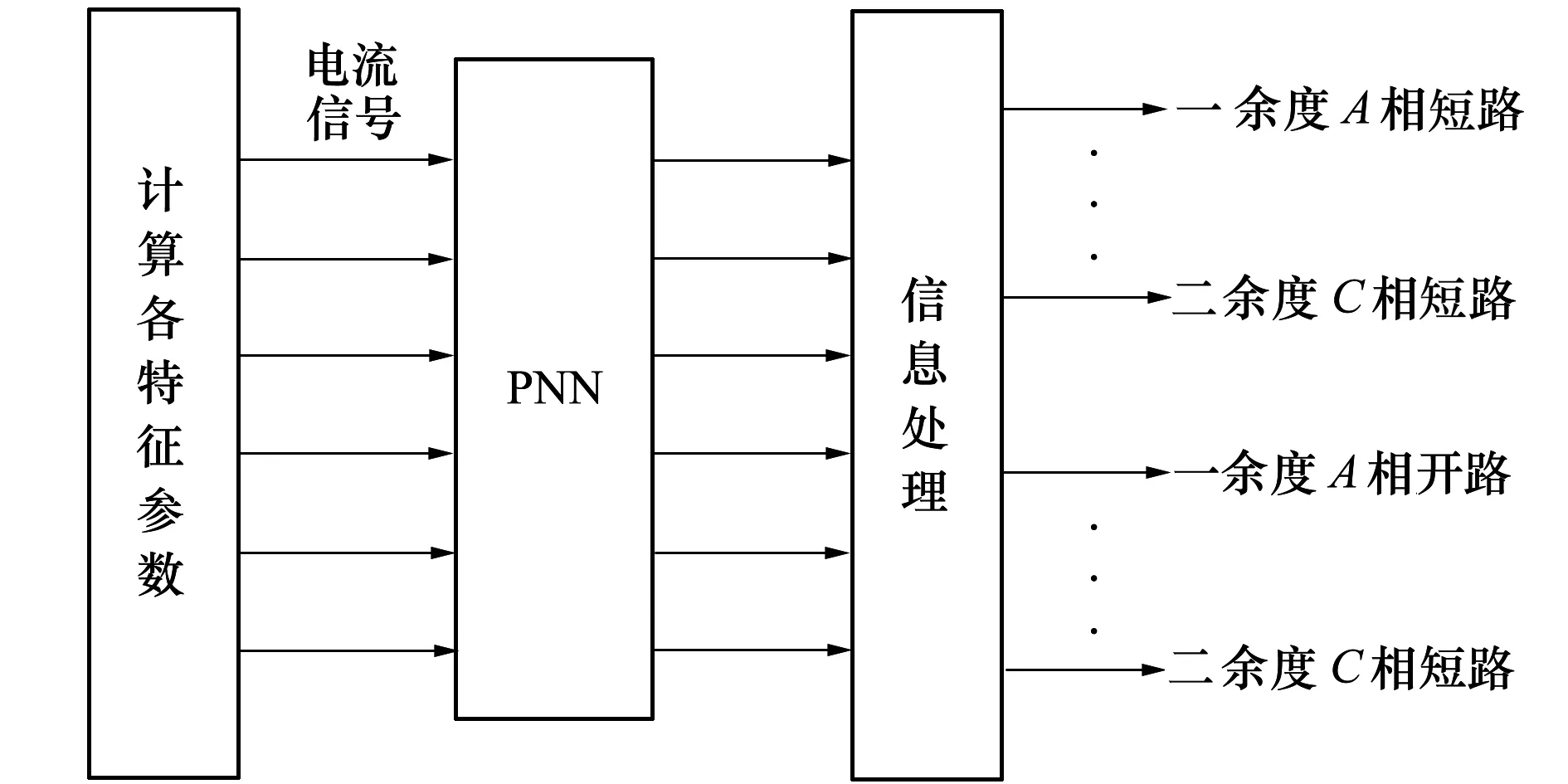
图8 PNN诊断模型

采用30个故障样本对PNN网络进行训练，然后采集一组测试样本，诊断结果如表4所示。诊断结果准确可靠。

表4 诊断结果

4 结 论

本文针对双余度永磁无刷直流电机中常见的绕组匝间短路故障进行了研究。针对傅立叶变换的不足，提出了用小波变换进行故障检测的方法；根据电机的故障树，确定了电流作为其故障诊断信号；通过对不同小波基函数的对比分析，选择coif5作为小波基函数；利用Mallat算法对多种典型电机故障信号进行了检测，采用第2层分解时的高频系数d2作为特征值，得到了各种故障时的特征向量。

根据电机故障信号的特点，选择小波神经网络作为其故障诊断方法，采用了松散型的结合方法；利用小波变换采集了多组故障信号特征向量并进行了归一化处理；建立了基于PNN神经网络，诊断结果表明模型能准确地识别绕组匝间短路故障。

参考文献：

[1] 王巍，郭宏，李艳明，于凯平．电气双余度无刷直流电动机转子极弧系数研究[J]．电机与控制学报，2009，13(6)：862-866

Wang Wei, Guo Hong, Li Yanming, Yu Kaiping. Research on Rotor Pole Arc of Electrical Dual-redundancy Brushless DC Motor[J]. Electric Machines and Control, 2009，13(6)：862-866 (in Chinese)

[2] Guo Hong, Wang Wei, Xing Wei, Li Yanming. Design of Electrical/Mechanical Hybrid 4-Redundancy Brushless DC Torque Motor [J]. Chinese Journal of Aeronautics, 2010,23:211-215

[3] 马瑞卿，刘卫国，解恩．双余度无刷电动机位置伺服系统仿真与试验[J]．中国电机工程学报，2008，28(18)：98-103

Ma Ruiqing, Liu Weiguo, Xie En. Simulation and Test of Position Servo System Based on Dual-Redundancy BLDCM[J]. Proceedings of the CSEE，2008，28(18)：98-103 (in Chinese)

[4] 王巍，郭宏，李艳明. 电气/ 机械混合四余度无刷直流力矩电动机绕组短路分析[J]．航空学报，2010，31(5):975-982

Wang Wei, Guo Hong, Li Yanming. Analysis of Winding Short-Circuit in Electrical/Mechanical Hybrid 4-Redundancy Brushless DC Torque Motor[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(5): 975-982 (in Chinese)

[5] Li Shichao, Shi Xiuhua, Cui Haiying. Diagnosis Based on Genetic Algorithms Wavelet Neural Network in Dual-Redundancy Brushless DC Motor[J]. Journal of Vibration Measurement & Diagnosis, 2009,29(2): 223-226