相干干扰下窄带信号检测统计处理与阵列处理的一致性研究

李明杨, 孙超, 刘宗伟, 易锋, 李芮

(西北工业大学 航海学院, 陕西 西安 710072)

在奈曼皮尔逊准则下，单输入和多输入系统窄带信号(含未知参数)检测的准最佳检测器均是周期图检测器[1]。二者的区别在于，多输入系统通过对接收信号做空域滤波处理，提高了检测器输出端的信噪比，这也是雷达、声呐领域中广泛使用的处理方式。然而，当检测空间中存在与目标信号频率相同的指向性干扰时，将使得目标方位所对应的检验统计量淹没于干扰之中。此时，传统周期图检测器将出现检测性能急剧下降，甚至失效的情况。为了减小或消除干扰带来的检测性能损失，需要在处理过程中尽可能克服干扰的影响。目前，这一处理思路可以分别从统计信号处理和阵列信号处理2个角度实现。但是，已有工作均是从2个不同的角度独立考虑相干干扰存在时的信号检测问题，本文通过理论推导和仿真实验，验证了两者在本质上是相通的，证明了2种处理器之间的一致性。

从统计信号处理的角度来看，可以对同频干扰存在的情况重新建立检测模型，推导得到相应的(准)最佳检测器。本文考虑的检测问题是一个典型的含有未知参数的确定性信号检测问题，即目标信号与干扰信号均是幅度、相位未知的窄带信号(目标与干扰方位以及信号频率文中假设已知)。针对这类检测问题，通常采用的处理方法是广义似然比检验方法(GLRT)与贝叶斯方法。两者的区别在于前者不需要未知参数的先验知识并且所获得的检测器是准最佳的，而后者获得的检测器是最佳的，但需要未知参数的先验知识。针对本文所考虑的检测问题(缺乏目标与干扰的先验知识)，选择GLRT方法进行分析求解。尽管此时推导得到的检测器是准最佳的，但是，GLRT检测器的检测性能已经足够好，事实上，GLRT检测器在某种意义下已经达到了最大一致势检验[1]。

从阵列信号处理的角度分析，传统周期图检测器在该检测环境下失效的原因是因为该检测器中所采用的常规波束形成器不具备抑制指向性干扰的能力，因此，只要将该波束形成器替换为具有抑制干扰能力的波束形成器即可适应该环境下的检测。对于抑制干扰的波束形成器的研究已经较为完善，可供选择的有：Capon提出的MVDR方法[2]，Olen等人提出的控制不同方位波束响应的静态波束图数字综

合方法[3]，Elko等人提出的自适应零限波束形成[4]，鄢社锋等人提出的运用二阶锥规划法综合各项性能指标的波束优化设计方法[5-6]，以及含有波束零点的Bartlett波束形成器[7]等。针对本文提出的问题，我们选择含有波束零点的Bartlett波束形成器来替换传统周期图检测器中的常规波束形成器，它具有运算量小、稳健性好、易于设计等诸多优良的性质，并且对相干干扰的抑制能力十分突出，更为重要的是，它是"最佳"的波束形成器：当设置波束零点的个数与基阵阵元个数相比较小时，它的阵增益与常规波束形成器的阵增益相比没有明显变化，且实现方式只是在常规波束形成器的基础之上增加了若干零点约束。

上述2种处理角度的侧重点是不同的：统计信号处理强调的是如何根据空间中各个传感器的采样数据来判断目标信号的有无；而在阵列信号处理中，关心的重点则是如何首先选择恰当的波束形成器来抑制干扰，然后实现对目标信号的检测。对于文中给出的检测问题，本文通过理论推导，分别得到了统计信号处理和阵列信号处理所对应的准最佳检测器，证明了这2种检测器是一致的，并将从统计处理角度推导得到的检验统计量所服从的统计分布中含有的非中心参量与阵列处理中的阵增益联系起来，建立了两种信号处理方式中参量之间的相互关系，这也是本文的核心思想所在。并通过计算机仿真验证了文中给出的2种检测器一致的结论。针对不同的阵元个数、目标方位(干扰方位固定)进行了计算机仿真，研究了上述参数对文中给出的检测器检测性能的影响，并分别从统计处理与阵列处理的角度给出了相应的解释，最后对全文进行了总结。

1 检测器的推导

1.1 信号观测模型

考虑采用M元均匀线列阵(ULA)对指向性相干干扰下的窄带信号进行检测，建立如图1所示的坐标系，1～M表示基阵阵元序号。图中s(n)与I(n)分别表示目标信号与干扰信号，θs与θi分别表示目标信号与干扰信号的入射方位角(相对于基阵法线方向)。假设干扰与目标均处于阵列的远场，且信号从正前方-90°～90°的观测区域入射。因此，干扰信号与目标信号到达接收阵时可视为平面波。

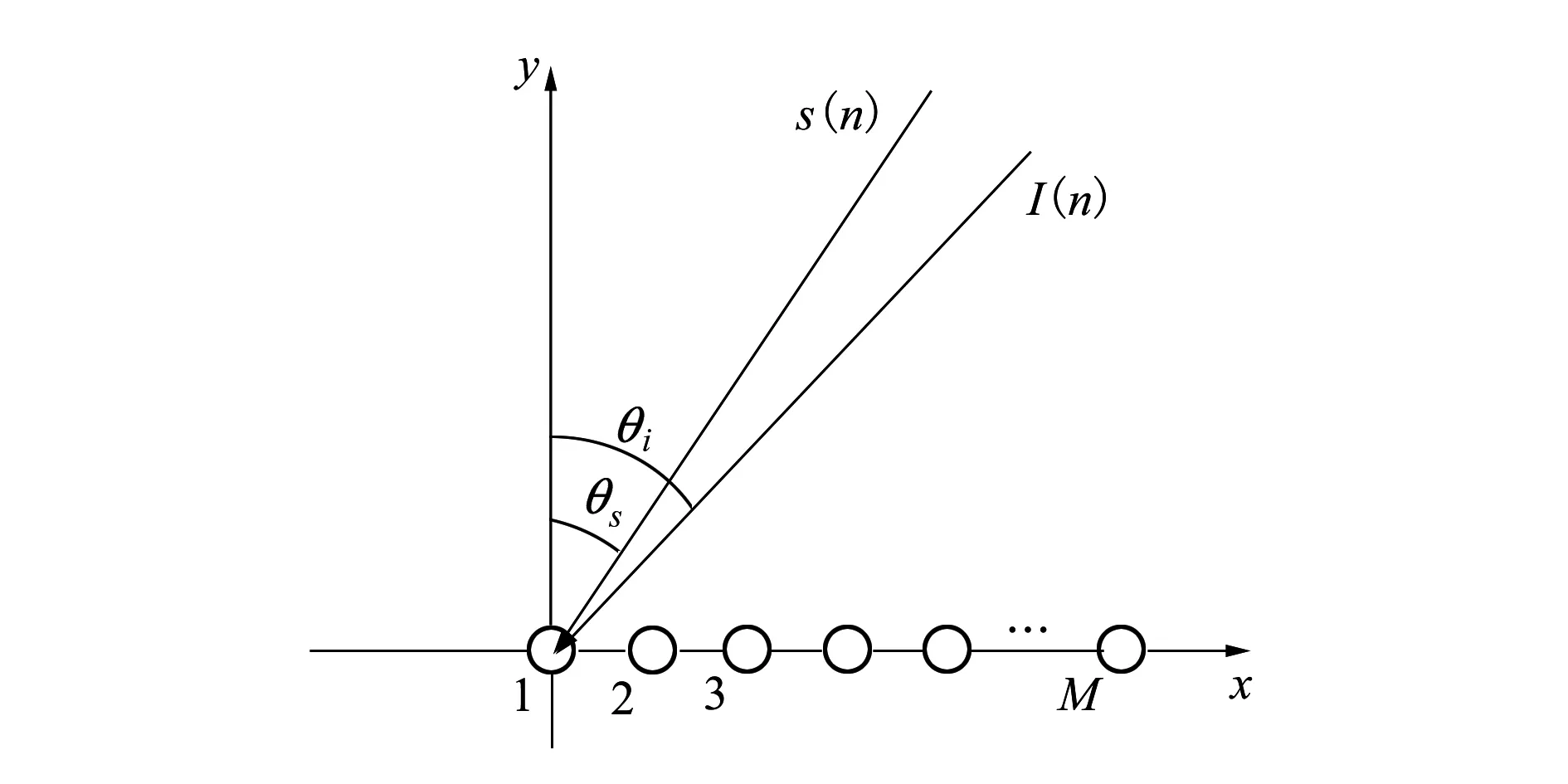
图1 基阵坐标系

(1)

式中：As、Ai分别表示目标信号与干扰信号的幅度，φs、φi分别表示目标信号与干扰信号的初相位，f0表示归一化信号频率，n为离散采样时刻。

(2)

(3)

式中：φs=2πfc·τ(θs)、φi=2πfc·τ(θi)，将(3)式代入到(2)式，可以得到

(4)

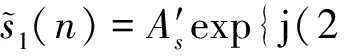
(5)

(6)

1.2 统计信号处理角度的检测器推导

由于在1.1节中,已经将接收信号模型表示为经典线性模型(classical linear model, CLM),因此,可直接采用CLM的GLRT定理对文中描述检测环境下的GLRT检测器进行推导[1]。

针对本文提出的检测问题,建立检测模型如下:

(7)

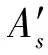
(8)

分析即可确定出A=[1 0]。运用CLM的GLRT定理[1]可以确定出(8)式所描述的检测问题的GLRT检验统计量为:

(9)

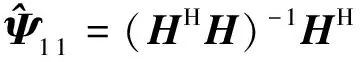
为了证明针对(7)式所描述的检测问题,从统计信号处理与阵列信号处理2个不同角度推导得到的检验统计量是一致的,进行以下数学推导:将观测矩阵H以及向量A代入到(9)式中,即可得到

(10)

检验统计量可以简单地记为(10)式右端项。令

(11)

并对(10)式右端项乘以1/N,有

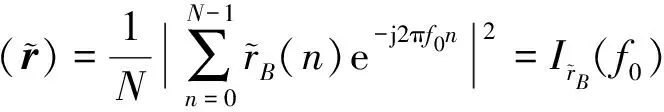
(12)

1.3 阵列信号处理角度的检测器推导

由于传统周期图检测器中所含有的常规波束形成器不具备抑制干扰的能力,因此,当检测空间中存在相干干扰时,检测器可能会出现工作异常的情况。在阵列信号处理领域中,通常采用波束形成技术来实现特定方向上的空域滤波。因此,从阵列处理的角度出发,可以在传统周期图检测器的前端空域滤波器中加入单个波束零点,并约束该零点指向干扰信号的入射方位,以此来过滤相干干扰,从而使改进后的检测器能够适应该环境下的检测。特别地,针对使用较多的ULA,国内一些学者将该空域滤波器称为含有波束零点的Bartlett波束形成器[7-8]。该波束形成器的加权向量为[7]

(13)

式中：B=I-a(aHa)-1aH,a=[v(φ1),v(φ2),…,v(φd)],v(φn)(n=1,2,…,d)表示期望形成波束零点方向θn所对应的基阵响应向量,φn=2πfc·τ(θn),I为单位矩阵。当波束形成器仅在干扰方向θi形成波束零点时,a=v(φi),此时,将a的表达式代入B中,由(13)式即可得到相应的加权向量为

(14)

根据(14)式可以得到含有波束零点的Bartlett波束形成器的输出为

(15)

(16)

(16)式即是对(7)式表述的检测问题从阵列信号处理的角度对波束形成器进行优化适配得到的检验统计量。

2 相干干扰下窄带信号检测统计处理与阵列处理的一致性讨论

对比(12)式与(16)式可知:对于(7)式描述的检测问题,从统计信号处理以及阵列信号处理2个不同角度推导得到的检验统计量是线性相关的,即:

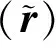
(17)

由于在保持虚警概率不变的情况下,对某个检测器乘以常系数后得到的检测器与原检测器具有相同的检测性能,因此,针对相干干扰下窄带信号的检测问题,从统计信号处理和阵列信号处理的角度推导得到的检测器是相同的,它们具有一致性。相比之下,从统计信号处理的角度来推导理论性更强,从阵列信号处理的角度来推导更为简洁与直观。

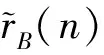
对于(8)式描述的检测问题,根据CLM的GLRT定理,可以确定出

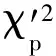
(18)

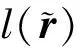
(19)

对于给定的虚警概率,可以确定出相应的检测门限γ,根据(18)式可进而可以确定出检测概率为

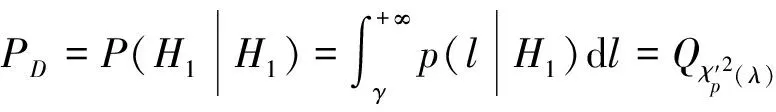
(20)

由服从非中心化卡方分布的随机变量的概率密度函数可知:当自由度p与检测门限γ给定时,非中心参量λ越大,服从该分布的随机变量的右尾概率就越大,即检测概率随非中心参量的增大而增大。下面将阐明阵增益与非中心参量之间的联系。

对于(14)式给出的权向量,可以求得相应的阵增益AG为

(21)

需要说明的是，第1节中关于检测器的推导均是在干扰与目标方位已知的假设情况下进行的。但通常情况下，不仅目标信号的幅度、相位未知，其方位、频率也是未知的，因此，实际检测中需要在感兴趣的方位、频率2个维度上对检验统计量的最大值进行搜索。相应地，检验统计量应修正为：

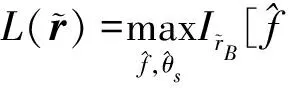
(22)

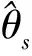
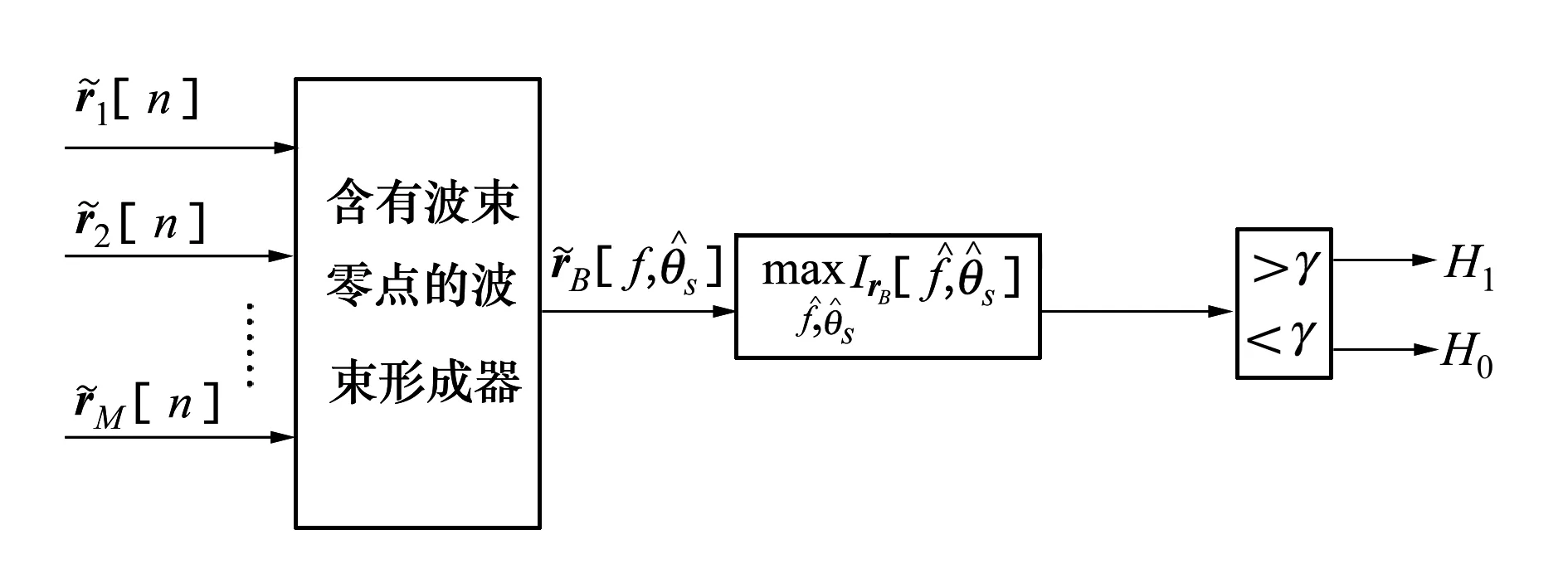
图2 相干干扰下窄带信号检测准最佳检测器

3 仿真实验

3.1 检测器的一致性验证仿真实验

为叙述简便，将(9)式描述的检测器称为该检测环境下的准最佳检测器，将(16)式描述的通过改进波束形成器得到的检测器称为适配改进检测器。本节在理想情况下(目标、干扰方位已知)分别对准最佳检测器((9)式)以及适配改进检测器((16)式)的检测性能进行计算机仿真，并将二者进行对比，以验证本文给出结论的正确性。

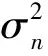
图3 目标方位变化时(干扰方位固定)2种检测器检测性能比较

由图3可知：(1)2种检测器的检测性能曲线基本重合，忽略由于实验次数不足带来的统计误差，可认为2种检测器的检测性能是相同的。仿真结果表明，本文给出的2种检测器一致性的结论是正确的；(2)随着目标与干扰逐渐靠近，检测器的检测性能有所下降，如图3c)、图3d)所示，但对比图3a)、图3b)可发现，并非目标与干扰一旦靠近就会出现检测性能明显下降的情况。

3.2 参数对检测器检测性能的影响仿真实验

本节改变目标所在方位以及阵元个数等参数，对3.1中的结论(2)进行进一步的研究，探究上述参数对检测器检测性能的影响。

设定干扰位于30°方位，信噪比为-5 dB，保持其余仿真参数与图3所对应的仿真实验一致，图4同时给出了2种检测器检测概率与目标信号入射角度之间的关系曲线。

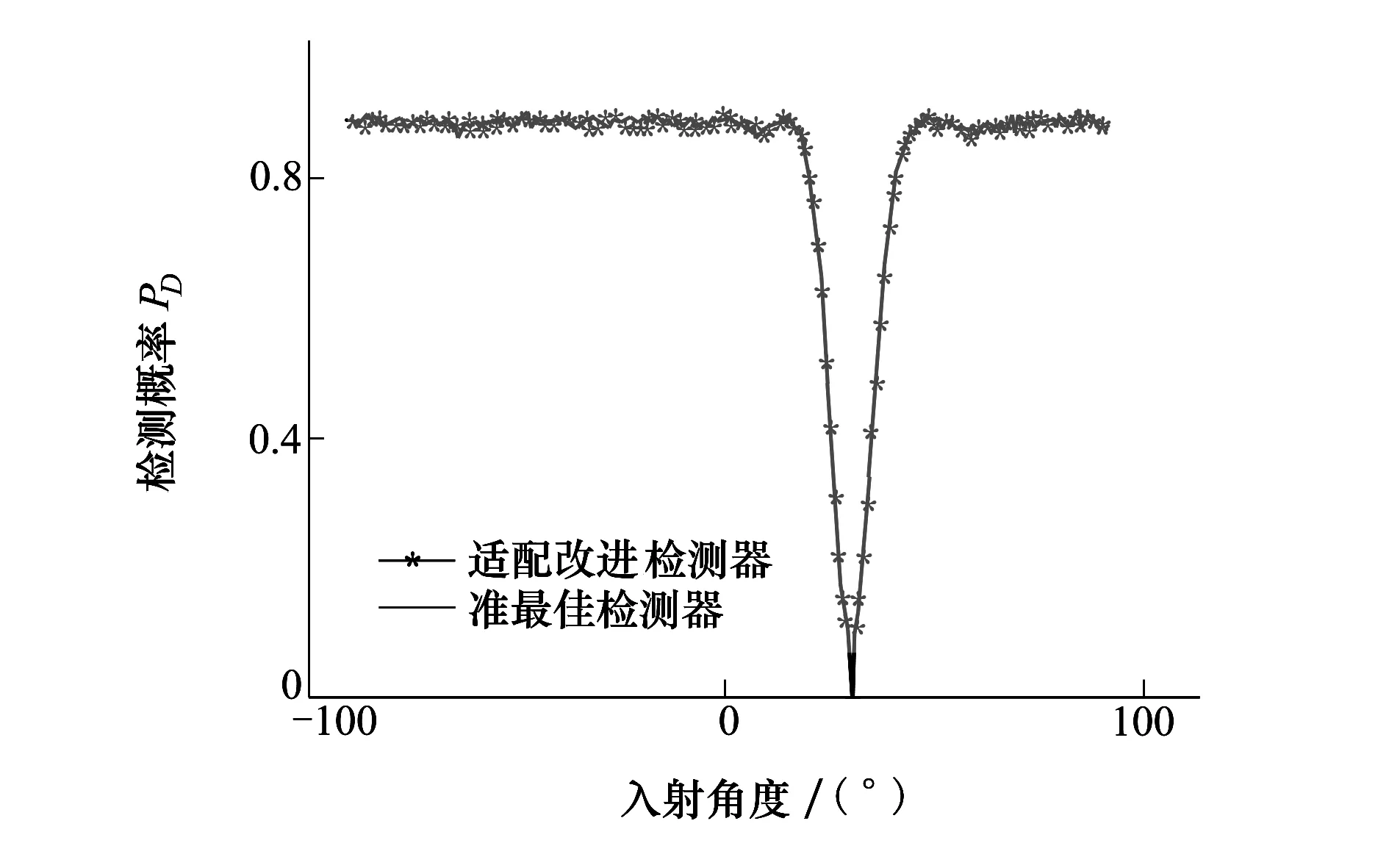
图4 PD与目标方位关系曲线

图4表明：当目标信号从离干扰较近的方位入射时会出现检测器检测性能大幅降低的情形，而从离干扰较远的方位入射时可以保持较好地检测性能。此结论对准最佳检测器与适配改进检测器同时成立。

这种检测性能的降低不仅与目标和干扰方位的相邻程度有关，并且与阵元个数也有关。在图4所对应的仿真实验基础上，仅改变基阵阵元个数，对该问题进行仿真研究，仿真结果如图5所示。由于2种检测器的一致性已经得到了验证，因此，该仿真仅针对适配改进检测器。

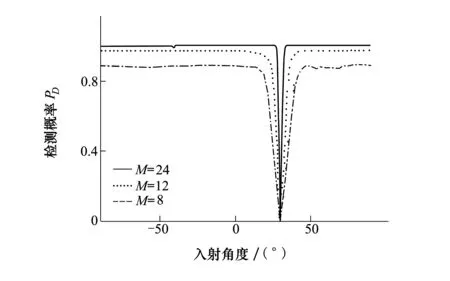
图5 PD与目标方位关系曲线(适配改进检测器)

图5表明：对于给定的干扰方位及阵元个数，存在目标方位的上下临界值，将上下临界值构成的区间称为目标方位的临界区间。当目标信号从临界区间内入射时，检测器的检测概率会明显下降，反之，检测器的检测概率将保持相对稳定(存在轻微波动)。对于阵元个数较多的基阵，该临界区间要比阵元个数较少的基阵更小。根据(21)式可以较为容易地推导得到目标方位的上下临界值

(23)

由(23)式可知，当干扰方位θi给定，M的取值越大，临界区间越小，这与仿真实验的结果(如图5所示)吻合。需要指出的是，(23)式的隐含假设是d=λ/2。可见，对于本文描述的检测器，阵元个数较多的基阵对于目标信号入射角度的临界区间具有更好的宽容性。可以从统计处理的角度以及阵列处理的

角度分别对该现象做出解释：

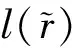
2) 阵列处理：分析构成检测器的波束形成器即可发现，波束零点不可能无限制地接近波束主瓣方向。当采用阵元个数较多的基阵来设计该波束形成器时，由于主瓣宽度很窄，分辨率很高，因此，波束零点可以适当地靠近主瓣而不会使主瓣增益、指向方位发生畸变，从而可以保证检测概率的相对稳定。但是，如果采用阵元个数较少的基阵来设计相同的波束形成器，主瓣指向、阵增益很容易就受到波束零点的影响，从而影响整个检测器的检测性能。

4 结 论

本文通过理论推导证明了：对于相干干扰下窄带信号的检测问题，从统计信号处理以及阵列信号处理的角度推导得到的检测器是一致的，并将由统计信号处理角度推导得到的检验统计量服从的统计分布中所含的参数信息——非中心参量与阵增益联系起来，建立起该检测问题统计处理与阵列处理的一致性，相应的计算机仿真验证了结论的正确性。

通过对影响检测器检测性能的参数进行仿真实验，得到了如下结论：①当目标信号由其临界区间内入射时，检测器的检测性能将随着目标逐渐靠近干扰而逐渐下降；②该检测器更适用于阵元个数较多的基阵处理上。对于阵元个数较多的基阵，目标与干扰可以比阵元个数较少时更为接近而不至于损失检测性能。针对上述结论分别从统计处理与阵列处理的角度给出了相应的解释，并推导得到了针对均匀线列阵目标信号入射方位上下临界值的计算公式。

参考文献：

[1] Kay S M. Fundamentals of Statistical Signal Processing, Volume II: Detection Theory[M]. New Jersey: Prentice Hall. 1998

[2] Capon J. High-Resolution Frequency-Wavenumber Spectrum Analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408-1418

[3] Olen C A, Compton R T. A Numerical Pattern Synthesis Algorithm for Arrays[J]. IEEE Trans on Antennas and Propagation, 1990, 38(10): 1666-1676

[4] Elko G W, Pong A T N. A Simple Adaptive First-Order Differential Microphone[C]∥IEEE ACSP Workshop on Applications of Signal Processing to Audio and Acoustics, 1995: 169-172

[5] Yan S F, Ma Y L, Sun C. Optimal Beamforming for Arbitrary Arrays Using Second-Order Cone Programming[J]. Chinese Journal of Acoustics, 2005, 24(1): 1-9

[6] 鄢社锋,马远良. 传感器阵列波束优化设计及应用[M]. 北京: 科学出版社,2009

Yan Shefeng, Ma Yuanliang. Sensor Array Beampattern Optimization Theory with Applications[M]. Beijing: Science Press, 2009 (in Chinese)

[7] 梅继丹,惠俊英,王逸林,等. Bartlett波束形成的波束零限权设计[J].哈尔滨工程大学学报,2008,29(12):1315-1318

Mei Jidan, Hui Junying, Wang Yilin, et al. Designing Null-Forming Weights Based on Bartlett Beamforming[J]. Journal of Harbin Engineering University, 2008, 29(12): 1315-1318 (in Chinese)

[8] 张贤达,保铮. 通信信号处理[M]. 北京:国防工业出版社,2000

Zhang Xianda, Bao Zheng. Communication Signal Processing[M]. Beijing: National Defence Industrial Press, 2000 (in Chinese)