基于扩展有限元研究非均质材料的应力强度因子

苏毅, 王生楠, 刘俭辉

(西北工业大学 航空学院, 陕西 西安 710072)

为了更好地了解非均质材料的力学性能,常用有限元法对这种材料进行仿真分析。但是,常规有限元法网格依赖性使之在处理连续-非连续问题时表现出明显的局限性。扩展有限元(XFEM)在处理这类不连续问题表现了极大的优势。因为XFEM[1-3]所使用的网格与结构内部几何或物理界面无关,从而克服了裂纹尖端等高应力和变形集中区内网格划分的困难,使得在模拟裂纹生长过程中无需对网格进行重新划分。网格划分也无需与材料细观结构的内部边界相协调。XFEM在处理不连续问题上的优点使其从问世以来,在国际上得到了很快的发展和广泛的应用。Zhang H.H.等人[4]用XFEM模拟了粘弹性材料的夹杂问题。2006年,文献[5]用扩展有限元对正交各向异性材料中的裂纹采用了新的加强法。用算例证明了他的准确性。王志勇等[6]运用不含裂尖增强函数的扩展有限元法,分别研究了静态及动态载荷作用下颗粒增强复合材料的断裂行为。假定基体和颗粒都为线弹性材料并且绑定完好,研究了不同颗粒位置、数量对基体裂纹尖端断裂参数的影响。数值模拟结果清晰地显示了含刚性颗粒和柔性颗粒时不同的失效机制。

本文的主要内容:①建立了含夹杂的带裂纹问题的位移场给出了均匀材料的相互作用积分和非均质材料的相互作用积分;②介绍了本文的相互作用积分的离散问题；③用3个算例模拟了带颗粒夹杂加强的裂纹板,软硬颗粒对应力强度因子或能量释放率的影响。

1 XFEM的基本原理

1.1 单位分解法

1996年Melenk和Babuska[7]及Duarte和Oden[8]先后提出了单位分解法(PUM),其基本思想是任意函数φ(x)都可以用域内一组局部函数Ni(x)φ(x)表示,即

(1)

式中：Ni(x)为有限元形函数,它形成一个单位分解

(2)

基于此,可以对有限元形状函数根据需要进行改进。XFEM是基于PUM对单元的形函数加以改进,从而考虑所研究问题的不连续、奇异性和边界层等特性。

1.2 位移逼近方程的建立

符合单位分解概念的向量函数u的逼近具有下列形式:

(3)

式中:Ni为有限元形函数,φα为改进函数,M表示改

进函数个数,根据(3)式,有限元空间(φ1≡1,其他φα≡0)将是改进空间的子空间。

XFEM的重点就集中在用最少的加强函数来描述不连续问题如裂纹位移逼近函数。用不连续函数和二维渐进裂纹尖端位移场来建立各向同性线弹性的裂纹模型。用水平集函数来建立材料界面的局部改进函数,这使得在裂纹扩展时不需要重新划分网格。

图1 裂纹和颗粒需要改进的自由度的节点集

扩展有限元的位移逼近为:

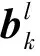
当节点为常规单元的节点时,只有第1项;当节点为被裂纹贯穿单元的节点时,有第1项和第2项;当节点为裂纹尖端所在单元的节点时,有第1项和第3项;节点同时处于裂纹贯穿单元和裂纹尖端所在单元,应优先属于裂纹尖端所在单元,加强方式选择裂纹尖端所在单元节点加强方式。当节点属于夹杂单元节点时,有第1项和第4项。也就是说当板中只有裂纹的话只需要前3项,当板中只有夹杂的话需要第1项和第4项,当板中同时有裂纹和杂质时,4项都需要。

1.3 XFEM离散方程的建立

和常规有限元方法一样,将(4)式代入弹性体的虚功方程,可导出XFEM的支配方程为

Kδ=F

(5)

式中：δ是节点位移列阵,K和F分别为结构总刚度矩阵和节点载荷列阵,K按常规步骤由单元刚度矩阵组集而成。单元层次上的k和f分别为

(6)

单元荷载列阵f:

(7)

子矩阵和单元荷载力矢量分量表示如下:

(8)

(9)

(10)

(11)

(12)

常规应变矩阵:

(13)

裂纹贯穿单元附加应变矩阵:

(14)

裂纹尖端单元附加应变矩阵:

(15)

夹杂单元附加的应变矩阵:

(16)

1.4 裂纹尖端应力强度因子计算

传统的J-积分形式为:

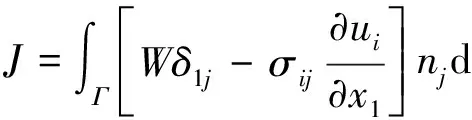
(17)

式中:Γ是积分路径,nj是该路径上弧元素外法线的方向余弦。加入辅助场后得到J-积分形式为:

(18)

选取辅助场形式为:

(19)

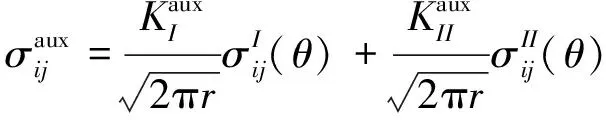
(20)

将(18)式展开,交叉部分为相互作用积分可以表示为:

(21)

式中：q为权函数,mi为单位法向量。当裂尖的积分区域包含夹杂颗粒区域,也同时包含了2种材料的界面。因此积分区域是非均质材料的积分。此时如果材料在空间上具有光滑变化的属性时,同时将线积分转化为面积积分。相互作用积分可表示为:

(22)

Ih为均匀材料的相互积分,Inonh为材料非均匀性衍生出的项。

εij=Sijkl(x)σkl(i,j,k,l=1,2)

(23)

从上面的定义发现,辅助应力场(20)式由于不涉及材料属性,是平衡的。但除了裂尖点之外,辅助位移场和辅助应变场之间的关系部再成立。定义裂尖处的应变场。

(i,j,k,l=1,2)

(24)

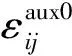
(25)

Ih为均匀材料的相互积分,Inonh也可以表示为:

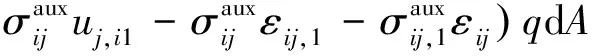
(26)

考虑不计体力的平衡状态及应力张量的对称性,有

此时上式可简化为:

εjkδ1j),iqdA

(27)

因为

(28)

经过变换包含材料界面的相互作用积分表达式为:

(29)

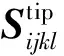
(30)

至此,可以看出当裂纹尖端距离颗粒很近时,(29)式的积分仍是可行的。但如果裂尖距离颗粒非常近或已经落在材料界面上时,应力不再满足反平方根奇异性,则需选取相对应的辅助场计算。当积分区域包含材料界面,如图2所示。

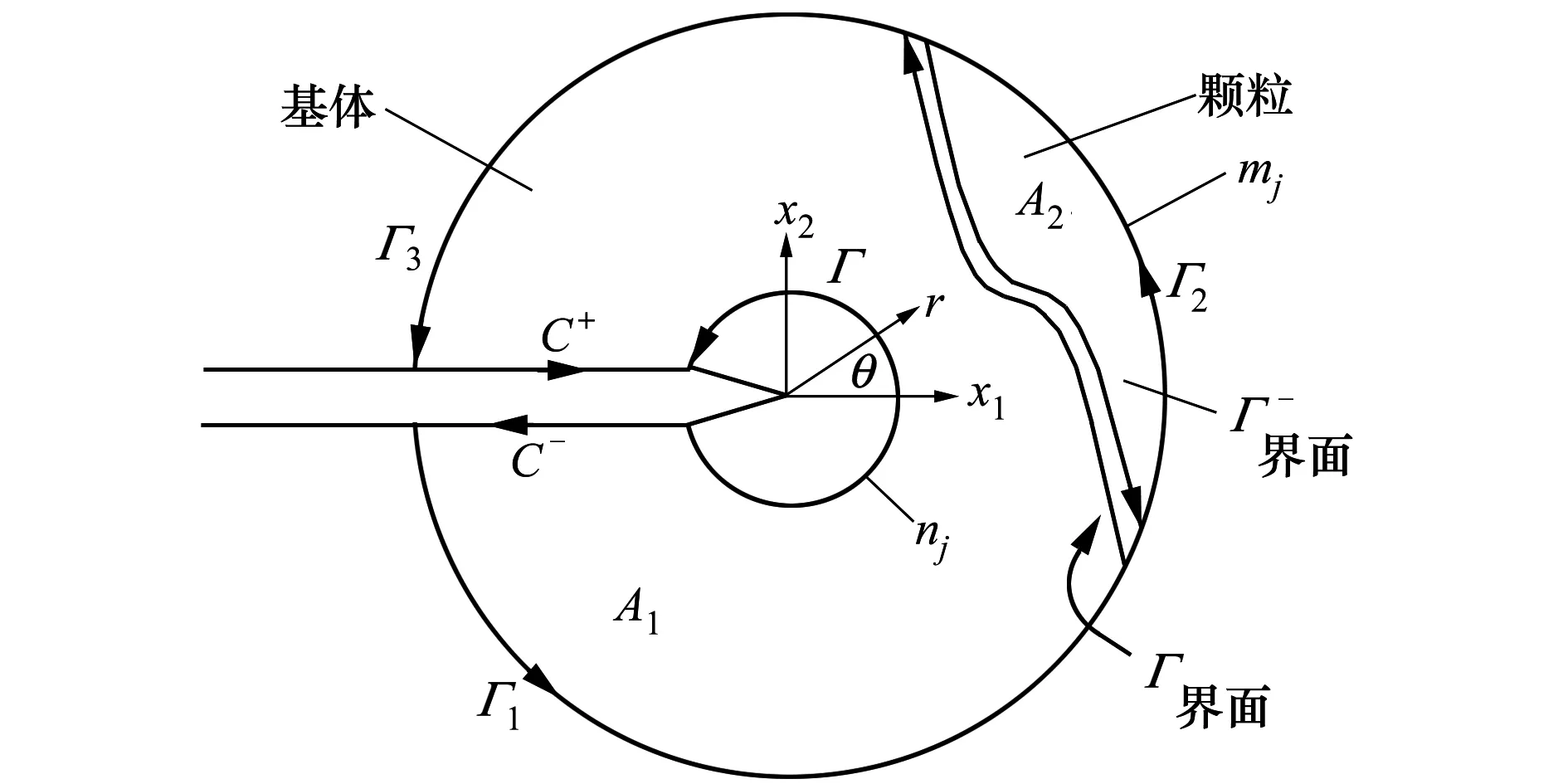
图2 裂尖局部坐标系及相互作用积分区域

对于各向同性材料相互作用积分与应力强度因子的关系可以表示为:

(31)

式中：

(32)

1.5 裂纹扩展方向

判断裂纹扩展方向常用的准则有:最大周向拉应力准则、最大周向拉应变准则、最小应变能密度强度准则、等应变能密度线上最大周向拉应力准则、能量释放率准则等[10],其中以最大周向拉应力准则计算最为简便。在最大周向拉应力准则里,裂纹尖端扩展方向θc由下式确定:(非均质有颗粒)

(33)

为了模拟裂纹的扩展过程,可采用裂纹增量形式。

2 相互作用积分的数值离散

在XFEM中为了很好地运用相互作用积分,(29)式可以被离散为:

(34)

式中：eA是积分区域A的的单元的数量;pe在单元中积分点的数量;|J|p为雅克比行列式;wp为积分点p的权重。实际位移的导数为:

(35)

对于非均质材料,建立刚度矩阵时,材料属性按照积分点的材料属性选取。由于在形函数的变分矩阵中含有不连续的函数,对裂纹分割单元,夹杂单元如果直接进行高斯积分,计算的结果是不准确的。文献[11-13]给出了积分策略。在本文中,对于常规单元采用2阶Gauss积分,对于混合单元采用6阶Gauss积分,对于裂纹贯穿和夹杂的单元,进一步细分成子三角形单元,每个子三角形单元采用3阶Gauss积分,对于裂尖单元,进一步细分成子三角形单元,每个子三角形单元采用7阶Gauss积分。

3 数值算例

算例1 无限大板中心裂纹与单个圆形颗粒间的相互作用

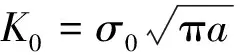
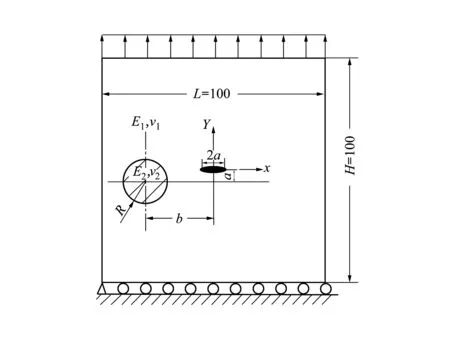
图3 带圆形夹杂颗粒的中心裂纹板

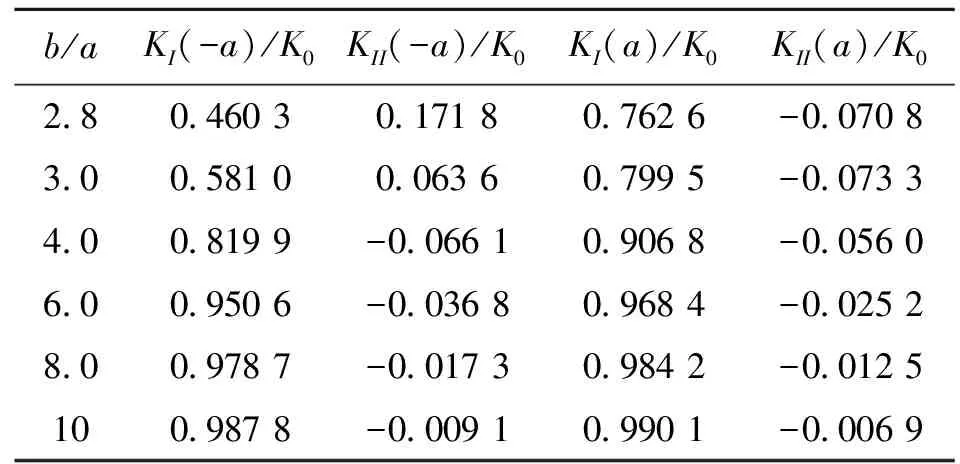
表1 Wang和Chau[14](E2/E=∞,υ=0.35)

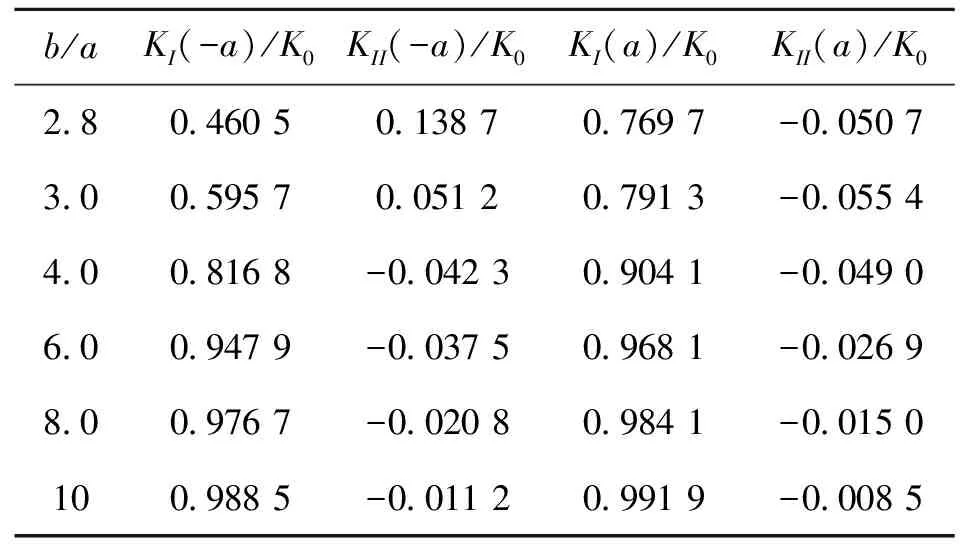
表2 本文结果(E2/E1=104,υ=0.35)

通过比较发现,本文结果和Wang和Chau[14]的结果相对误差很小,证明了合理性。当b/a增大时,KI(-a)/K0和KI(a)/K0随之增大,说明当裂纹与颗粒的位置越远时,颗粒加强的作用会减小。

算例2 单边裂纹扩展与单个圆形颗粒间的相互作用

如图4所示,一个二维平板尺寸为H×L,受到单向拉伸载荷σ作用,其内部含一个长度为a的边裂纹,圆形颗粒半径为R。颗粒中心与裂纹尖端垂直距离为b,H=15;L=15;b/R=1;a/L=1/15;R=a;EP/E=100,10,5或是EP/E=0.01,0.1,0.2下标P代表板的弹性模量υ1=υ2=0.35;σ=1;KI0为没有颗粒夹杂时裂纹尖端的应力强度因子,裂纹扩展60次,每次步长为0.2。

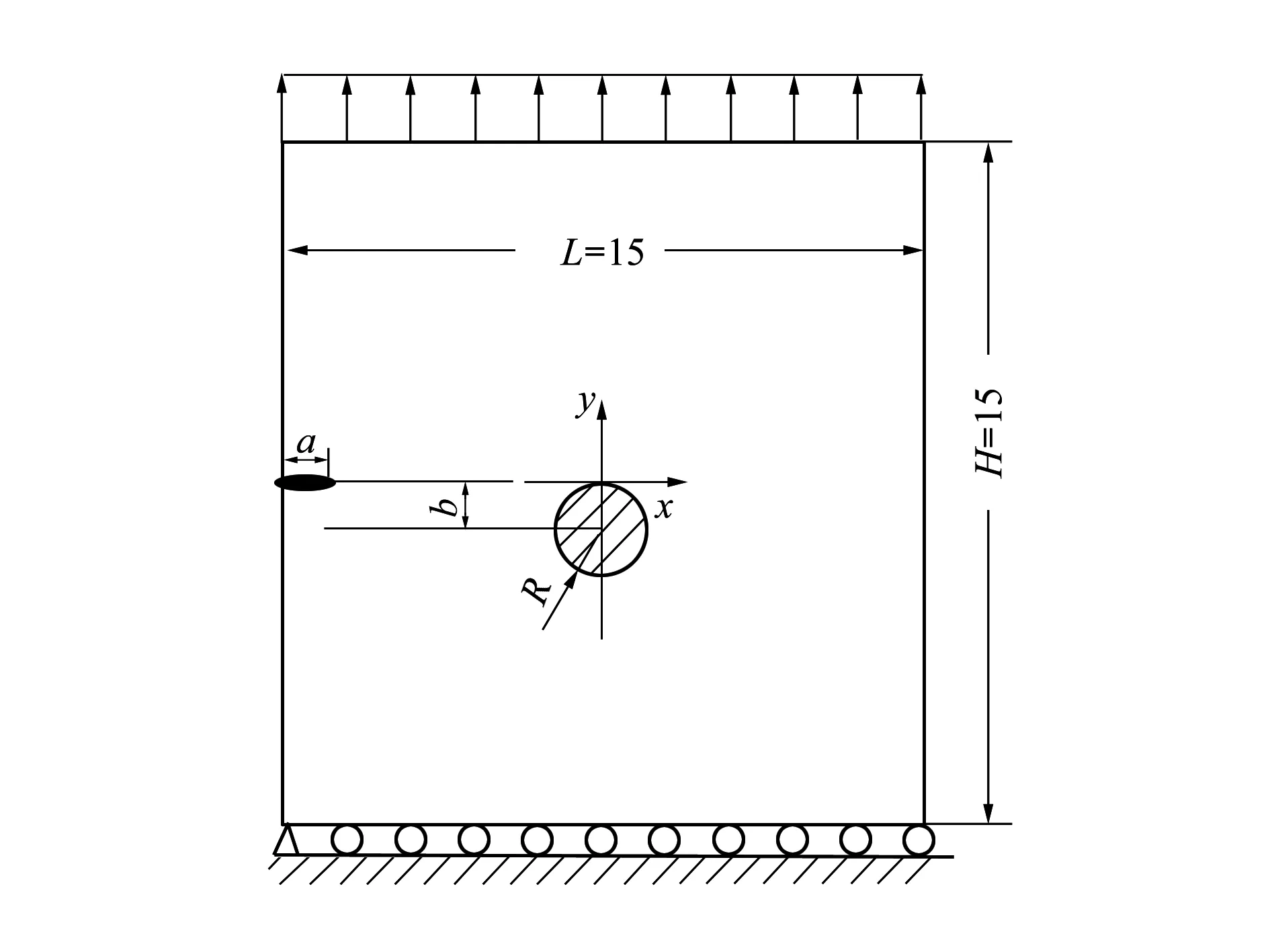
图4 带圆形夹杂颗粒的单边裂纹板

图5表示在软硬颗粒下,裂纹扩展轨迹。在软颗粒的时候,裂纹扩展偏向颗粒,颗粒弹性模量越小最后裂纹越靠近颗粒。这证明了裂纹的扩展偏向于强度小的地方,在无颗粒的情况下,裂纹的路径基本没有什么改变,在匀质板的情况下,裂纹路径没什么改变。同样硬颗粒的时候,裂纹扩展远离颗粒。颗粒的弹性模量越大最终越偏离原来轨迹。

图6表示无量纲量KI/KI0随着x/R变化趋势, 对于硬颗粒而言,应力强度因子一直比无颗粒的时候小,说明了硬颗粒的确对板有加强作用,颗粒的弹性模量越大对板的加强效果越明显。而对软颗粒而言,应力强度因子比无颗粒加强时大,软颗粒降低了板的强度,从图中可以看出在x/R在-2到0的区间,颗粒对板的加强或减弱作用明显。

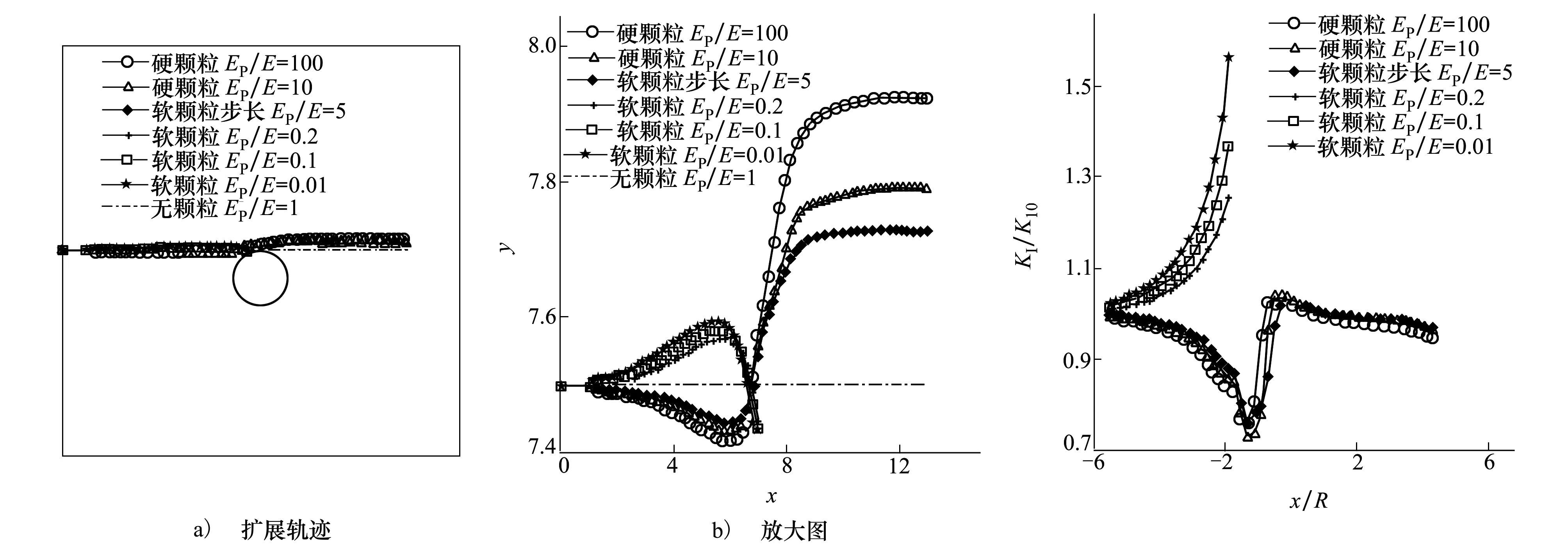
图5 裂纹扩展轨迹图6 裂纹扩展时,KI/KI0的变化

算例3 孔边单裂纹扩展与单个圆形颗粒间的相互作用

如图7所示,一个二维平板尺寸为L×H,受到单向拉伸载荷σ作用,其中心有一个孔洞半径为R孔边有一长度为a的裂纹,圆形颗粒半径为R。其离孔洞中心的水平距离为b=4.5,H=15;L=15;a/W=1/30;R=a;Ep/E=100,10或是Ep/E=0.01,0.1;下标p代表颗粒的弹性模量;υ1=υ2=0.35;σ=1;G0为没有颗粒夹杂时裂纹尖端的能量释放率,裂纹扩展16次,每次步长为0.2.c=0.2,0.5。

图8表示无量纲量G/G0随着x变化趋势,对于硬颗粒而言,能量释放率一直比无颗粒的时候小,说明了硬颗粒的确对板有加强作用,颗粒的弹性模量越大对板的加强效果越明显。G/G0随着x增大越来越小,也就是随着裂纹尖端越靠近硬颗粒,硬颗粒对裂纹尖端的能量释放率的影响越明显。距离c对G/G0影响也很明显,c越小影响越明显。而对软颗粒而言,能量释放率比无颗粒加强时大,软颗粒降低了板的强度,随着裂纹尖端越靠近软颗粒,硬颗粒对裂纹尖端能量释放率的影响越明显。 因为裂纹板是不对称的,裂纹的扩展路径是偏离水平方向的。

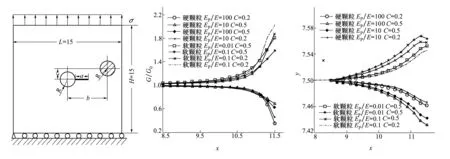
图7 带圆形夹杂颗粒的孔边单裂纹板 图8 裂纹扩展时,G/G0的变化 图9裂纹扩展的轨迹(放大)

4 结 论

1) 应力强度因子是基于2个相容许的场实际场和辅助场。

2) 用扩展有限元计算裂纹扩展时很方便,不用在裂纹尖端重新划分网格。

3) 颗粒对材料的强度的增加或减弱有很明显的作用。

参考文献：

[1] Daux C, Mo⊇s N, Dolbo W J, Sukumar N, Belytschko T. Arbitrary Branched and Intersecting Cracks with the Entended Finite Element Method[J]. International Journal for Numerical Methods in Engineering, 2000, 48: 1741-1760

[2] Mo⊇s N, Dolbow J, Belytschko T. A Finite Element Method for Crack Growth without Remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46:131-150

[3] Sukumar N, Srolovitz D J, Baker T J, Prevost J H. Brittle Fracture in Polycrystalline Microstructures with the Extended Finite Element Method[J]. International Journal for Numerical Methods in Engineering, 1999, 45: 601-620

[4] Zhang H H, Li L X. Modeling Inclusion Problems in Viscoelastic Materials with the Extended Finite Element Method[J]. Finite Elements in Analysis and Design, 2009, 45: 721-729

[5] Asadpoure A, Mohammadi S. Developing New Enrichment Functions for Crack Simulation in Orthotropic Media by the Extended Finite Element Method[J]. International Journal for Numerical Methods in Engineering, 2007, 69:2150-2172

[6] 王志勇,马力,吴林志,于红军. 基于扩展有限元法的颗粒增强复合材料静态及动态断裂行为研究[J]. 固体力学学报,2011,32(6): 566-573

Wang Zhiyong, Ma Li, Wu Linzhi, Yu Hongjun. Investigation of Static and Dynamic Fracture Behavior of Particle-Reinforced Composite Materials by the Extended Finite Element Method[J]. Chinese Journal of Solid Mechanics, 2011, 32(6):566-573 (in Chinese)

[7] Melenk J M, Bubska I. The Partition of the Unity Finite Element Method: Basic Theory and Applications[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139: 289-314

[8] Duarte G A, Oden J T. An H-P Adaptive Method Using Clouds[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139: 237-262

[9] Yu H J, Wu L Z, Guo L C, Du S Y, He Q L. Investigation of Mixed-Mode Stress Intensity Factors for Nonhomogeneous Materials Using an Interaction Integral Method[J]. International Journal of Solids and Structures, 2009, 46:3710-3724

[10] 张行. 断裂力学[M]. 北京:中国宇航出版社, 1990

Zhang Hang. Fracture Mechanics[M]. Beijing: China Aerospace Press, 1990 (in Chinese)

[11] Laborde P, Pommier J, Renard Y, Salaun M. High-Order Extended Finite Element Method for Cracked Domains[J]. International Journal for Numerical Methods in Engineering, 2005, 64: 354-381

[12] Mousavi S E, Xiao H, Sukumar N. Generalized Gaussian Quadrature Rules on Arbitrary Polygons[J]. International Journal for Numerical Methods in Engineering, 2010, 82: 99-113

[13] Natarajan S, Bordas S, Mahapatra D R. Numerical Integration over Arbitrary Polygonal Domains Based on Schwarz-Christoffel Conformal Mapping[J]. International Journal for Numerical Methods in Engineering, 2009, 80:103-134

[14] Wang Y B, Chau K T. A New Boundary Element Method for Mixed Boundary Value Problems Involving Cracks and Holes: Interactions between Rigid Inclusions and Cracks[J]. International Journal of Fracture, 2001, 110: 387-406