基于滑模变结构的IPMC 跟踪控制系统设计

王瑷珲，张 强，王东云，刘 萍

(中原工学院 电子信息学院，河南 郑州451191)

0 引言

离子聚合物金属材料(IPMC，Ionic -exchange Polymer Metal Composite)是一种离子型电致动聚合物，已经被人们赋予人工肌肉的美名［1］． 在低电压驱动下，能够产生较大的位移变形，作为一种新型执行器非常适用于仿生机器人的开发与应用［2-3］．为了精确控制IPMC 人工肌肉的位置，将传统的PID 控制应用到高度复杂的非线性以及模型不确定性系统中，效果是不够理想的，尽管传统PID 控制器具有一定的鲁棒性和适应性，但是对于强非线性、快速时变不确定性、强干扰等特性的对象，控制效果较差．由于变结构控制能够克服系统的不确定性，对干扰和未建模动态具有很强的鲁棒性，且具有快速响应，无需系统辨识，物理实现简单等优点，尤其是对非线性系统的控制具有良好的控制效果，已经广泛应用于非线性系统的控制设计中［4-8］．因此，针对IPMC 复杂非线性模型以及模型不确定性，采用滑模变结构对IPMC人工肌肉位置进行跟踪控制，并采用指数趋近律方法来抑制滑模变结构控制过程中产生的抖振现象，进而设计了基于神经网络的PI(Proportional-Integral)外环跟踪控制器，实现了不确定性因素下参数的自整定，鲁棒性较好．最后通过仿真结果验证了所设计系统的有效性．

1 IPMC 动态模型

在IPMC 人工肌肉的精确位置控制中，主要存在线性和非线性两种模型． 非线性模型相对线性模型而言能够比较详细地解释了IPMC 人工肌肉的动作原理和工作机理． 一种IPMC 的非线性模型可以描述为［9］

式中:v 是状态变量;u 是控制输入电压;y 是控制输出曲率;Ra是限流电阻;Rc是电极电阻;Ke是介电常数;Ye是等效模量;h 是IPMC 人工肌肉的厚度;Δ 是有界未知的模型不确定量;函数Γ(v)、C1(v)分别表述为式中:F 是法拉第常数;R 是气体常数;T 是绝对温度;C-1是负离子浓度． 将式(2)、(3)代入式(1)中并令x=av，可得到如下非线性模型:

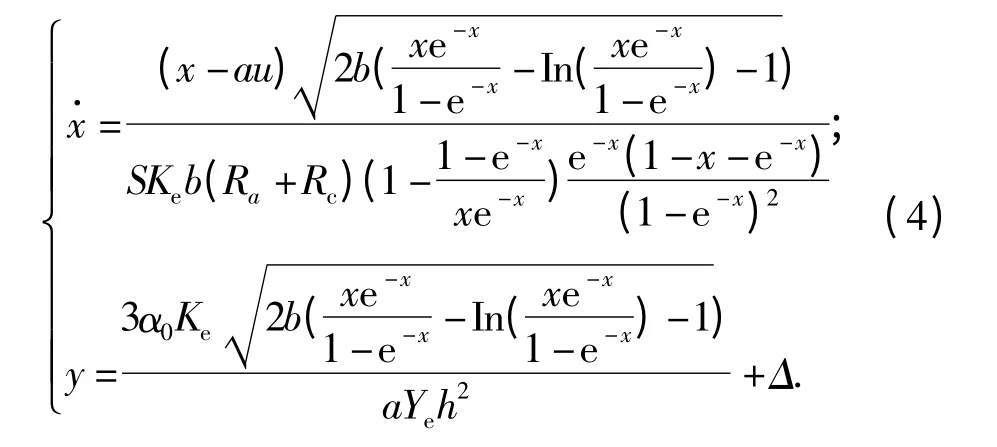
2 滑模变结构控制器设计

设计滑模变结构控制器的基本步骤包括:①设计切换函数s(x)，使它所确定的滑动模态渐近稳定且具有良好的动态品质． ②设计滑动模态控制律u(x)，使到达条件得到满足，从而在切换面上形成滑动模态区．

2．1 切换函数的设计

滑模函数设计为s(t)=ce(t)，其中，c ＞0 满足Hurwitz 条件．误差及其导数分别为

2．2 滑动模态控制律的设计

采用指数趋近律，不仅可以改善系统的动态品质，还可以有效地抑制抖振，其形式为

从而保证s s·≤0． 即满足滑模存在性和可达条件．选取Lyapunov 函数:

对其求导有

根据上述分析，得

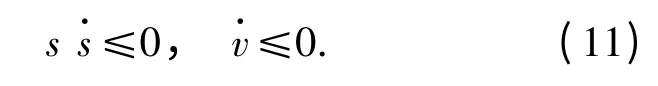
则证明基于指数趋近律的滑模控制在李雅普诺夫意义下是渐近稳定的．

由动态方程状态空间方程表达式

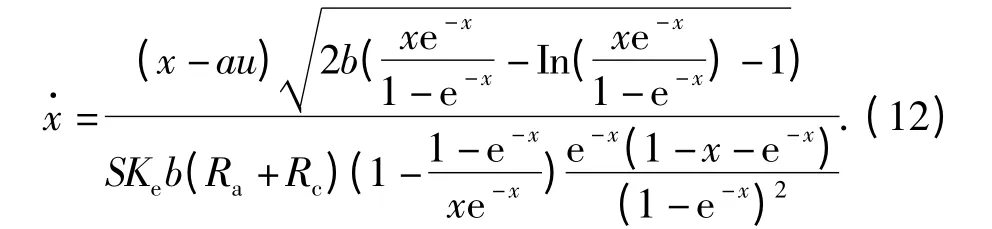
分别令A、B 为如下形式:

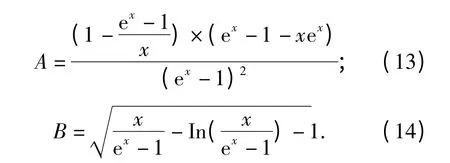
将辨识得到的模型参数以及A、B 代入式(12)得到等效关系式:

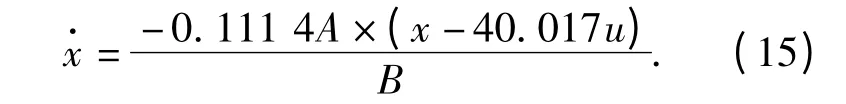
由式(7)和式(8)联立，得

将式(16)代入，得

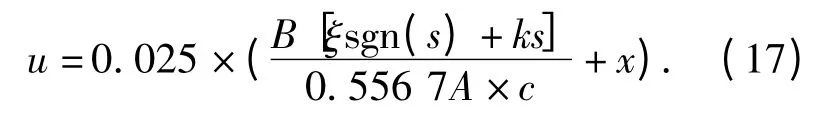
在实际系统中，假设存在外部干扰的情况下，控制器的设计如下:设d 为干扰，未知但有界． 设计滑模控制律为

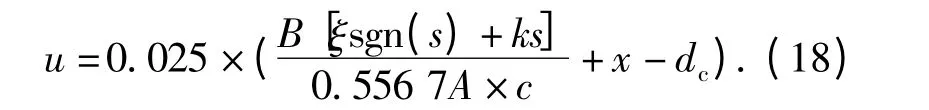
dc为设计的与干扰d 的界相关的正实数． 将式(18)代入式(15)、(16)，得

通过选取dc来保证控制系统稳定，即满足滑模到达条件．假设dmin≤d≤dmax，dc选择的原则为:

则可设计满足上述两个条件的控制器dc．dc=d2-d1sgn(s)． (23)

为了进而确保IPMC 的寿命，其控制电压u要进行限幅Q(t)=θ(u(t))．其中umax=3v，umin= -3v，输入受限约束条件如下所示:

滑模变结构控制系统如图1 所示． 采用滑模变结构对含有不确定性的非线性对象IPMC 人工肌肉进行位置控制．为了能够跟踪给定输入，设计了PI 外环控制器如图2 所示．图中的p～等效为框图1 所示系统，此方法的可行性已在文献［10］得到证明． 并采用BP 算法，应用最速下降法，按照减少目标输出与实际输出之间误差的方向，从输出层反向经过各中间层回到输入层，从而逐层修正各连接权值，对其参数进行自整定，实现跟踪控制．BP 算法实现步骤包括初始化;输入训练样本对，计算各层输出;计算网络输出误差;计算各层误差信号;调整各层权值;检查网络总误差是否达到精度要求;满足则结束，否则继续计算各层输出．设计的PI 外环控制器表达式为

u(k)=u(k-1)+Kp(e(k)-e(k-1))+Kie(k)．(25)

图1 滑模变结构控制系统结构图Fig．1 Sliding mode variable structure control system

图2 跟踪控制系统结构图Fig．2 Tracking control system

3 仿真分析

3．1 仿真参数

辨识的模型参数如表1 所示．

滑模变结构控制器3 个参数分别设置为ξ =10．802 6，k =11，c =26．601 6． BP 网络设置时笔者采用4 ×5 ×2 网络，即输入层4 层，隐含层5层，输出层2 层，学习速率η =0．2，惯性常数α =0．05，输入层Oj=［r(k)，y(k)，e(k)，1］，输出层Ol=［Kp，Ki］，初始权值wi和wo分别取为:

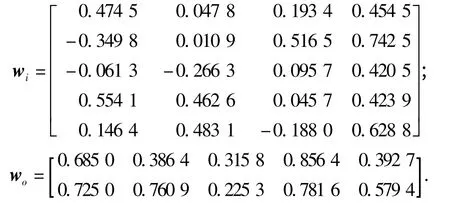
3．2 仿真结果

根据辨识的模型参数，采用滑模变结构分别对含有模型不确定性和不含模型不确定性的非线性对象IPMC 人工肌肉进行仿真，期望的控制输出曲率y 为1 m-1，如图3 所示．在鲁棒稳定的基础上，加入基于神经网络的PI 控制器，并将输入电压限幅在3 V 以内，实现跟踪控制，如图4 所示．

图3 鲁棒稳定特性仿真结果Fig．3 Robust stability result

图4 跟踪特性仿真结果Fig．4 Tracking result

在实际系统中，不仅有来自模型参数辨识产生的误差，模型结构的不确定性还有系统受到的外部干扰等不确定因素． 为了验证基于神经网络的滑模控制器的鲁棒性能，期望的控制输出曲率为y=0．5sin(0．25πt)+0．5，并在3 s ＜t ＜5 s 时给系统加上一个单位阶跃信号的控制器输出干扰，与传统PID 控制进行了对比，如图5 所示．可以看出，笔者提出的方法相比于传统方法而言，能够较好地跟踪给定，鲁棒性好．

图5 鲁棒性能比较Fig．5 Robust performance comparison

4 结论

针对高度复杂非线性IPMC 人工肌肉，建立其精确的数学模型非常困难． 采用传统PID 控制在模型不确定性以及外部干扰影响下很难达到精确位置控制．本文将近似模型建立过程中产生的模型误差等效为有界的不确定量，采用基于神经网络的PI 控制与滑模变结构控制相结合对含有模型不确定性的IPMC 人工肌肉进行控制． 滑模变结构控制用以实现鲁棒稳定，基于神经网络的PI 控制用以实现跟踪，应用所提方法，不仅能够对其精确跟踪，而且抗干扰性能好，鲁棒性强．通过仿真验证了设计系统的可行性．

［1］ 郝丽娜，周轶然．IPMC 的制备研究［J］．东北大学学报:自然科学版，2009，30(12):1728 -1730．

［2］ 唐华平，姜永正． 人工肌肉IPMC 电致动响应特性及其模型［J］． 中南大学学报:自然科学版，2009，40(1):153 -158．

［3］ BHAT N，KIM W． Precision force and position control of ionic polymer mental composite［J］． Journal of System and Control Engineering， 2004， 218 (6):421-432．

［4］ 刘广瑞，刘又午． 柔性臂关节位置滑模变结构控制研究［J］． 郑州大学学报:工学版，2003，35(4):58 -62．

［5］ 晁红敏，胡跃明． 动态滑模控制及其在机器人输出跟踪中的应用［J］． 控制与决策，2001，16(5):565 -568．

［6］ LEVANT A． Chattering analysis［J］． IEEE Transactions on Automatic Control，2010，55(6):1380-1389．

［7］ 李春华，孙约，罗琦． 非线性系统的反演自适应动态滑模控制［J］．计算机工程与设计，2009，30(1):185 -187．

［8］ FOUAD T，ALHAMMADI K，KARKI H． An optimized chattering free sliding mode controller to suppress torsional vibrations in drilling strings［J］． Conference and Exhibition，2011:573 -576．

［9］ WANG Ai-hui，DENG Ming-cong，WANG Dong-yun．Operator-based robust nonlinear control for ionic polymer metal composite with uncertainties and hysteresis［J］． Lecture Notes in Artificial Intelligence/Computer Science，2010，64(24):135 -146．

［10］DENG Ming-cong，INOUE A，ISHIKAWA K． Operator-based nonlinear feedback control design using robust right coprime factorization［J］． IEEE Transactions on Automatic Control，2006，51(4):645 -648．