基于SURF 和伪Zernike 矩的图像拼接算法研究

李喜艳，纪东升，吴崇正

(1．郑州成功财经学院 信息工程系，河南 郑州451200;2．兰州大学 信息科学与工程学院，甘肃 兰州730030)

0 引言

图像拼接是通过对多个具有互相重叠部分的图像进行配准，拼接成一个分辨率更高，视野更宽的图像．图像配准是图像拼接的重要步骤，基于特征点匹配的方法须先从图像上提取不变性特征，如特征角点、矩等，再进行精确匹配．在图像的各种不变性特征中，角点具有旋转不变性和几乎不受光照条件影响的优点，因此，基于特征点匹配的图像拼接在视频检索、景物匹配以及遥感图像融合等领域都具有十分广泛的应用． 为有效解决图像在旋转、平移变换及光度差异等情况下存在的拼接问题，提出了一种基于改进的SURF 检测［1］和伪Zernike 矩的图像拼接算法(SURF Feature Points Pseudo-Zernike Moments Algorithm，SPZMA)．该算法利用形态学极大值改进的SURF 算子提取图像特征点;然后计算中心邻域窗口的伪Zernike 矩，通过比较伪Zernike 矩的Bray-Curtis距离得到初始匹配点对;接着运用RANSAC 算法［2］剔除伪特征点对，建立图像对之间的变换模型，实现图像配准;最后，通过利用渐入渐出分段加权函数消除拼接缝，使拼接图像实现平稳过渡，SPZMA 算法流程结构如图1 所示．

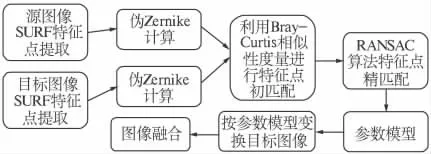
图1 SPZMA 算法流程图Fig．1 SPZMA algorithm flowchart

1 图像特征点检测和描述

1．1 SURF 特征点检测算法

(1)积分图像中任意一点(i，j)的值ii(i，j)为原图像左上角到任意点(i，j)相应的对角线区域灰度值的总和，即

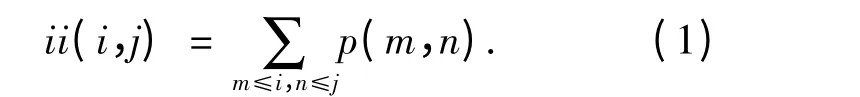
式中:p(m，n)表示原图像中点(m，n)的灰度值．

(2)给定图像I 中一个点x(x，y)，在点x 处，尺度为σ 的Hessian 矩阵H(x，σ)定义如下:

式中:Lxx(x，σ)是高斯二阶微分(σ)在点x处与图像I 的卷积，Lxy(x，σ)和Lyy(x，σ)具有同样的含义．

为了将模板与图像的卷积转化成滤波［2］运算，需要对高斯二阶微分模板进行简化，使简化后的模板只由几个矩形区域组成，矩形区域内填充同一值，用Dxx、Dyy和Dxy表示模板与图像卷积的结果，这样便可将Hessian 矩阵［3］的行列式作如下简化，其中w 为权重．

Det(Happrox)=DxxDyy-(wDxy)2． (3)

(3)将二维图像I (x，y)与高斯核卷积得到不同尺度的空间:L(x，y，σ ) = I (x，y)·G(x，y，σ )，其中，G(x，y，σ )为尺度可变的高斯函数，再通过建立高斯差分尺度空间寻找图像的局部极值．在图像高斯差分尺度空间内当前尺度和其相邻两个尺度3* 3 的区域内，标记的像素点和周围像素点比较，如果标记的像素灰度值大于或者小于其他像素，那么这个标记像素点就是特征点．

Step4 对上一步的小数组做2(w -1)次比较．这里对算法进行如下改进:

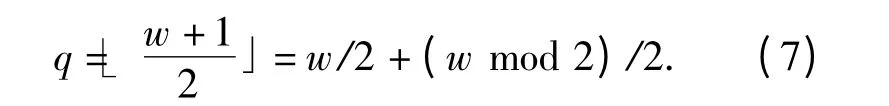
计算Rk和Qk平均需要进行max(w -q，q -1)+(w-1)+1 =1．5w -(w mod2)/2 次计算和比较，且小于2(w-1)．

Step5 窗口最大值的函数可表示为

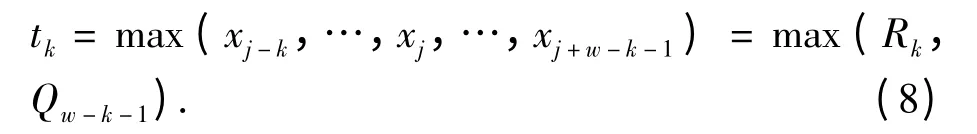
1．2 利用局部极值搜索窗口算法的改进

根据Hessian 矩阵求出尺度图像在(x，y，σ)的极值后，首先在极值点的3 ×3 ×3 的立体领域内进行非极大值抑制［4］． 为了能够对候选特征点进行亚像素定位，可以在尺度空间和图像空间中使用二次拟合函数进行插值:

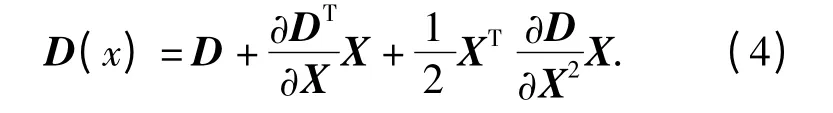
笔者基于形态学滤波中的局部极大值抑制的思想，采用改进的HGW(Herk-Gil-Werman)算法，将局部求极大值抑制的过程转化为在二维窗口内对局部极值的求取，用以加快算法的速度．

Step1 先将像素矩阵为X 的图像扩展为Y=［Y A］，之后将扩展矩阵均分为宽度为w 的多个子矩阵，A 是扩展的零矩阵．

Step2 将二维窗口划分为2 ×1． 极值二维窗口用下式定义为

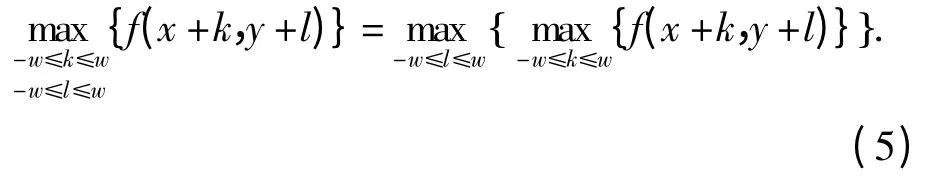
Step3 确定扩展矩阵Y 某行数组(x0，…，xn-1)的局部最大值． 用公式yi=xi+j(i =0，…，n-w)表示求最大值，且将x0，…，xn-1分成多个小数组xw-1，x2w-1，x3w-1，…．对每个小数组，定义如下序列元素Rk和QK(k=0，…，w-1 )．

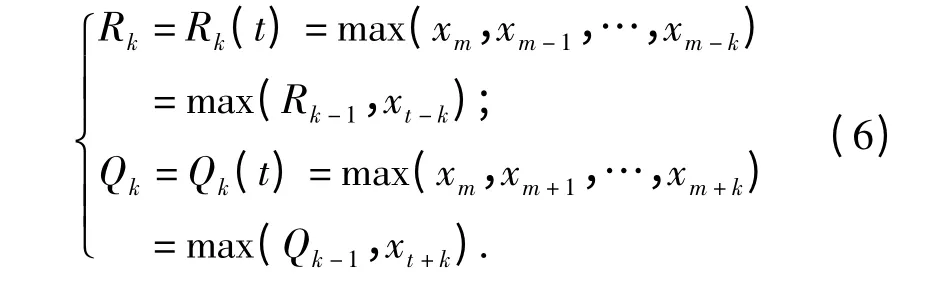
应用二叉树搜索定理可知，每个元素需要搜索「lb(w -1)⏋/w 次，进而可以在扩展矩阵Y 内确定最大值的新矩阵Z，故数组内每个元素平均比较次数为

1．5 +「lb(w-1)⏋/w-(w mod2)/(2w)． (9)

Step6 重复进行上述算法的Step1 至Step5，即可得到二维窗口局部极值的分布矩阵Z～，即Z～表示在某元素半径范围内的最大值的分布情况．

Step7 去掉分布矩阵Z～中的扩充矩阵，且与X 矩阵对应元素作减法，若有0 值，便为w ×w 窗口的局部最大值．

由于在垂直与水平方向上均进行了一次局部极值的求解，改进后的总的元素比较次数就为

3 +2「lb(w-1)⏋/w-(w mod2)/w． (10)

图2 为改进后的HGW 算法、原HGW 算法与普通算法实验结果对比．可以看到，改进后的算法单个元素的比较次数将趋向于3，比其他两种算法都要少．当窗口越来越大时，改进算法的性能优越性就越来越明显．

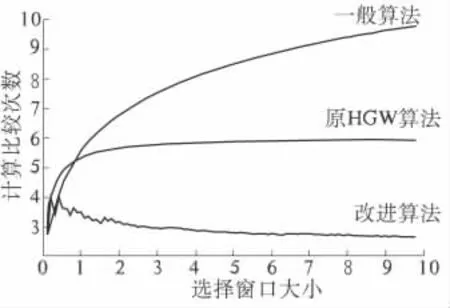
图2 3 种算法的实验效果比较Fig．2 Experimental results compare the three algorithm

实验表明，改进后的HGW 算法角点检测定位准确，自适应性好，角点提取速度更快，从而得到比原算法更理想的角点检测效果．图3 ～6 为本文算法对角点的偏移、lena 图像、旋转45°以及加入噪声的检测效果．

图3 表明，改进算法定位关键点角点更加准确．图4 和图5 可看出，本文算法提取的角点均匀，对图像旋转的适应性好．图6 中加入了乘性噪声(σ=0．02)，本文算法和原算法相比较，提取角点均匀合理，具有较强的抗噪能力．表1 为图像角点提取个数及平均运行时间的统计，运用快速窗口搜索算法的改进算法在运行速度上有了明显提高，虽然提取出的角点数量比原算法减少，但角点分布更加均匀，尤其对关键点角点检测没有漏检．

图3 本文改进算法与原算法对克服角点偏移结果比较Fig．3 The improved algorithm with the original algorithm compare the result to overcome offset corner

图4 本文改进算法与原算法对Lena 图像实验结果比较Fig．4 The experimental results on the Lena image rotation 45 degrees compare

图5 对Lena 图像旋转45 度的实验结果比较Fig．5 The experimental results on the Lena image rotation 45 degrees compare

图6 加入乘性噪声(σ=0．02)的实验结果比较Fig．6 The join multiplicative noise(σ=0．02)of the experimental results

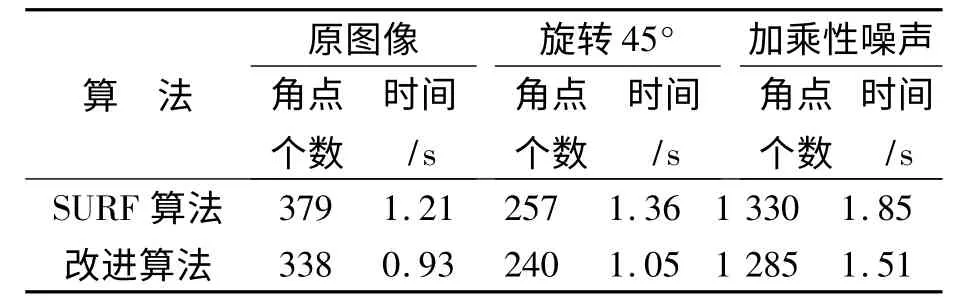
表1 检测Lena 图像角点个数及平均运行时间统计Tab．1 Lena image corner detection of the number of points and the average run time statistics

1．3 特征点描述

(1)特征点提取后，需要找出两幅图像特征点之间的对应关系，即特征匹配． Zernike 矩是一组正交矩，具有旋转不变性的特性，且Zernike 矩可以构造任意高阶矩，所以识别效果优于其他方法．笔者采用特征点邻域的不变矩作为匹配的特征，根据伪Zernike 矩的不变性，使它具有更多的矩数量及更好的抗噪声性能．

(2)伪Zernike 矩的选择．数字图像的像素离散性质使得伪Zernike 矩的计算产生误差，不同阶矩的计算精确度不同［5］，因此，必须对矩进行优化选择．选择矩时主要考虑两点:1)当矩的阶数高于某一个值Nmax时，计算量大且计算不再准确，实验中取10 阶;2)重复度为m =4i(i =0，1，2，…．)的矩计算是不准确的，应当去除． 而由于矩的共扼对称性，剩下的矩只有一半是独立的．记选取的矩集合为S，即S={Anm，n≤Nmax，m≥0，m≠4i}．

2 图像匹配

2．1 图像的快速匹配

为了达到好的特征点匹配效果，采用“粗—精”的方法以提高特征点匹配的可靠性［6］． ①用Bray-Curtis 相似性度量初步选取伪Zernike 矩描述的相似匹配特征点对;②采用RANSAC 算法进一步筛选伪匹配点对．

欧式距离度量通常被用于计算图像之间的相似度，然而，其不能对特征值进行归一化，会有一些高量级的特征点控制着低量级的特征点． 笔者运用Bray-Curtis 相似性度量，规范其特征值并通过区分不同的相对特征值和绝对值，以计算相似特征点对的匹配度． Bray-Curtis 的相似性度量公式(11)提出了基于特征点的描述:

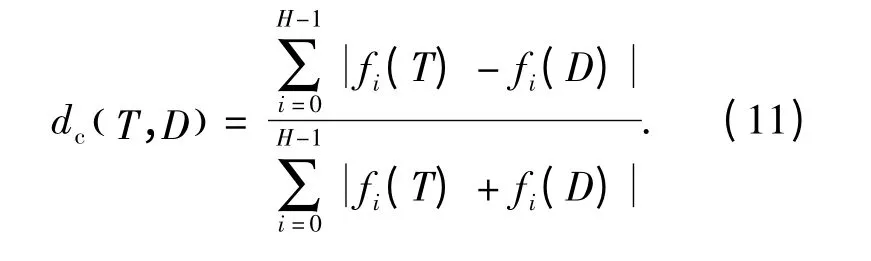
式中:fi(T)、fi(D)表示特征向量的测试和数据图像;H 是基于角点特征的数量．

Bray-Curtis 的相似性度量用于伪Zernike 矩:

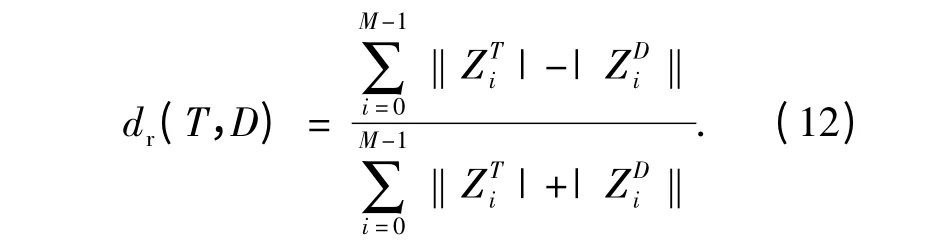
d(T，D)=wcdc(T，D)+wrdr(T，D)． (13)

式中:wc和wr代表权重的两图像的相似性度量．计算相似度和Bray-Curtis 相似性度量两个欧氏空间，比较它们的性能．这样可以计算出原图像中每一个特征点在目标图像中的匹配点，当然这样的匹配对中会包含部分伪匹配点对．

2．2 精确匹配

RANSAC 算法根据一组包含异常数据的样本数据集，计算出数据的数学模型参数，并得到有效的样本数据．利用齐次坐标，两幅图像之间的投影变换模型可以用矩阵的形式来描述［7］:

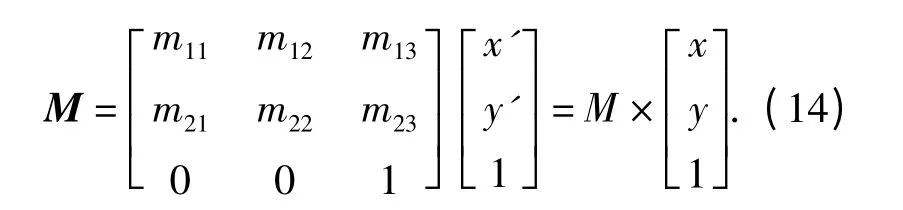
式中:参数m11，m12，m21，m22表示尺度缩放和旋转;m13为水平方向位移;m23为垂直方向位移．

以相邻两幅图像为例，设匹配特征点对数目为N，匹配特征点集合分别记为P(1，N)，P(2，N)．其中，P(1，N)为基准图像的特征点集合，P(2，N)为待匹配图像的特征点集合，算法步骤如下:

Step1 从初始N 对匹配特征点中随机选取3 对匹配特征点;

Step2 由选取的3 对匹配特征点计算出基准图像和待匹配图像间的相似变换矩阵M12，利用变换矩阵M12 将待匹配图像的特征点集合P(2，N)中剩余的N-2 个特征点P(2，N -2)变换到基准图像坐标系下，并记为P'(2，N-2);

Step3 计算变换后的特征点P'(2，N-2)与特征点P(1，N-2)之间的坐标误差;

Step4 从N 对匹配特征点对中找出坐标误差在一定误差阈值内特征点对个数，记为i;

Step5 反复迭代Step1 ～Step4 步，直至找到i 最大的集合为最大内点集即为内点，其余N -i为误匹配点即为外点．用最小二乘法来减少误差，去除了误匹配的影响，最终得到空间变换矩阵M．

3 图像融合

采用具有双线插值思想的渐入渐出方法［8］．设f1，f2是两幅待拼接的图像，将f1和f2在空间叠加，则融合后的图像像素f 可表示为

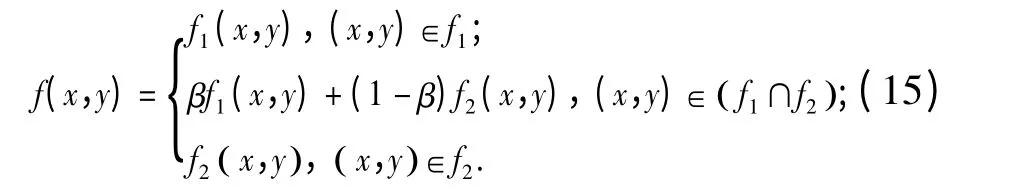
设图像间重叠区域宽度为L，两幅图像重叠区x 轴和y 轴的最小和最大值分别为xmin、xmax和ymin、ymax，则过渡因子的计算方法为

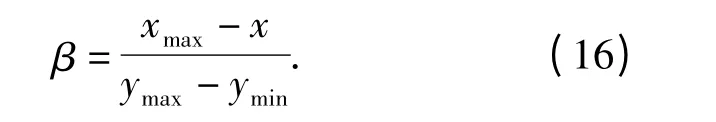
式中:β，(1 -β)表示过渡因子，一般与重叠区域的宽度有关，且0 ＜β ＜1．在重叠区域中，β 由1 渐变到0，(1 -β)由0 渐变至1，由此实现了重叠区域中由f1到f2的平滑过渡．

4 实验结果及分析

图7 ～9 是应用本文算法和归一化相似性算法(WC)分别对正常图像、扭曲图像及不同角度的旋转图像拼接效果进行对比．从图可看出，当图像没有旋转、扭曲或者色度均匀时不同算法的拼接效果相差很小;当图像有扭曲现象时本文算法对图像的拼接处理更优;当图像旋转角度达到30°时，NC 算法出现了图像失配情况，而本文算法仍能够实现对图像的拼接．实验结果表明:本文算法对图像有更好的旋转适应性．

图7 原图像采用本文算法与NC 算法的拼接比较Fig．7 Original image using the algorithm of this paper compared with NC algorithm of joining together

图8 扭曲30 度图像采用本文算法与NC 算法的拼接比较Fig．8 Distorted 30° images using this algorithm and the algorithm of NC joining together

图9 旋转30 度图像采用本文算法与NC 算法拼接比较Fig．9 30° rotation image compared with NC algorithm joining together using the algorithm of this paper

5 结论

提出了一种SPZMA 图像拼接算法，该算法利用改进的SURF 算子获取图像中的特征点，计算以特征点为中心邻域窗口的伪Zernike 矩，获得各个特征点邻域伪Zernike 矩的Bray-Curtis 相似性度量的初始匹配点对，利用RANSAC 算法剔除伪特征点对，之后对输入图像作几何变换进行配准，融合重叠区域，获得良好的拼接图像．实验结果表明:提取特征点均匀、准确、迅速;图像配准时对平移、旋转以及噪声均具有鲁棒性．

［1］ KNOPP J，PRASAD M，WILLEMS G，et al． Hough transform and 3D SURF for robust three dimensional classification［C］//Computer Vision-ECCV 2010-11th．Berlin Heidelberg:Springer，2010:589 -602．

［2］ WONG T C K． Box filter structure:U． S，Patent，7708，883［P］． 2010 -05 -04．

［3］ REININGHAUS J，KOTAVA N，GUNTHER D，et al．A scale space based persistence measure for critical points in 2d scalar fields［J］． IEEE Transactions on Visualization and Computer Graphics． 2011，17(12):2045 -2052

［4］ HEROUT A，HRADIš M，ZEMĉíK P． EnMS:early non-maxima suppression［J］． Pattern Analysis and Applications，2012，15(2):121 -132．

［5］ 纪东升． 基于特征点的图像拼接算法研究［D］． 兰州:兰州理工大学计算机与通信学院，2011．

［6］ SATTLER T，LEIBE B，KOBBELT L． Fast imagebased localization using direct 2D-to-3D matching［C］//IEEE International Conference on Computer Vision (ICCV)． Spain:IEEE Press，2011:667 -674．

［7］ YANG B，LI S． Multifocus image fusion and restoration with sparse representation［J］． IEEE Transactions on Instrumentation and Measurement，2010，59(4):884 -892．

［8］ ARIVAZHAGAR S，ANISHA J P． Image fusion using spatial unmixing［C］//Signal Processing Image Processing ＆ Pattern Recognition (ICSIPR)，2013 International Conference on IEEE． Coimbatore:IEEE Press，2013:238 -242．