Family Competition Pheromone Genetic Algorithm for Comparative Genome Assembly
2014-03-24ChienHaoSuChienShunChiouJungCheKuoPeiJenWangChengYanKaoandHsuehTingChu
Chien-Hao Su, Chien-Shun Chiou, Jung-Che Kuo, Pei-Jen Wang Cheng-Yan Kao, and Hsueh-Ting Chu
Family Competition Pheromone Genetic Algorithm for Comparative Genome Assembly
Chien-Hao Su, Chien-Shun Chiou, Jung-Che Kuo, Pei-Jen Wang Cheng-Yan Kao, and Hsueh-Ting Chu
——Genome assembly is a prerequisite step for analyzing next generation sequencing data and also far from being solved. Many assembly tools have been proposed and used extensively. Majority of them aim to assemble sequencing reads into contigs; however, we focus on the assembly of contigs into scaffolds in this paper. This is called scaffolding, which estimates the relative order of the contigs as well as the size of the gaps between these contigs. Pheromone trail-based genetic algorithm (PGA) was previously proposed and had decent performance according to their paper. From our previous study, we found that family competition mechanism in genetic algorithm is able to further improve the results. Therefore, we propose family competition pheromone genetic algorithm (FCPGA) and demonstrate the improvement over PGA.
Index Terms——Genetic algorithm, genome typing, next generation sequencing.
1. Introduction
The advent of next generation sequencing (NGS) technology has generated an enormous amount of data that give a large demand for the necessity of computer software to handle these data. This is because the next step usually overlaps and merges the deoxyribose nucleic acid (DNA) reads, small fragments of the genome, from NGS technology into a contiguous longer string, called contig. This step called assembly is far from being solved. Therefore, many assembly algorithms and software (including DNA and RNA (ribose nucleic acid) assembly)have been proposed and used extensively, such as Newbler[1], Celera Assembler[2], Velvet[3], ABySS[4], AllPaths[5],[6], SOAPdenovo[7], Oases[8], Trinity[9], and EBARDenovo[10], to name a few. For the comparison of most of the above tools and the introduction of assembly, please see reviews[11]-[14].
Majority of the assembly tools aim to assemble reads into contigs; however, we focus on the assembly of contigs into scaffolds. This is called scaffolding, which estimates the relative order of the contigs as well as the size of the gaps between these contigs. The estimation is usually based on the availability of one or several closely related genome sequences that is assumed to have high degrees of synteny. A few tools have been developed to achieve a good estimation for the order of the contigs, for example, Projector2[15], OSLay[16], AMOScmp[17], treecat[18], and PGA[19]. Projector2 is a web service that maps contigs on a reference genome by using BLAST (basic local alignment search tool) or BLAT (blast-like alignment tool)[20]. Projector2 also has several features, including a repeat masking option for contigs, a visualization interface of the mapping results, and an automated primer design step for gap-closure purposes. OSLay aims at computing a layout of contigs based on their synteny information by using maximum weight matching and also provides an interactive visualization of the layout. AMOScmp aligns reads to the reference genome by applying a modi fi ed MUMmer[21]algorithm. However, these methods are limited to the assembly of contigs derived from closely related genomes, i.e., different strains of the same species. For distinct species, assembly accuracy typically decreases dramatically.
To overcome this hurdle, Zhaoet al.proposed a pheromone trail-based genetic algorithm (PGA) to evaluate the distance between two contigs in the target genome and predict the most probable pairwise connections for all contigs using global search heuristics[19]. In addition, PGA accepts more than one genome as reference and can significantly improve the performance of contig assembly for more distantly related genomes. Zhaoet al.have demonstrated that PGA outperforms previous methods, such as Projector2, OSLay, and other BLAST end-based tools. Different from PGA, treecat uses sequence similarity as well as their phylogenetic information to estimate theadjacencies of contigs. In addition, instead of generating one optimal order of the contigs, treecat describes contig adjacencies by creating the contig layout graph. However, this would increase the false positive rate of the assembly results. It is still arguable that which format is more valuable, a single linear ordering to aid the closure of gaps or contig layout graph with more flexible at the expense of increasing the false positive rate.
Yanget al.improved the function optimization results by integrating the family competition into the genetic algorithm[22]. The family competition strategy was first introduced in Yanget al.’s previous paper[23]and can be viewed as a local competition mechanism when generating offspring in the genetic algorithm. They have also demonstrated that the family competition is capable of obtaining better performance and saving the computation time. Inspired by their study, we propose a novel genetic algorithm by integrating the family competition into PGA, called FCPGA (family competition pheromone genetic algorithm). The results show that lower fitness, which means better assembly result, is obtained when using FCPGA. We also find that using multiple mutations could significantly improve the performance of genetic algorithm in our study. Finally, the run time of FCPGA is shorter than PGA. Therefore, we demonstrate the robustness and power of the family competition.
2. Material and Method
2.1 Collection of the Data
Salmonella enterica serovar Typhi(S. typhi), a serotype ofSalmonella enterica, is a major cause ofSalmonella typhi(also called typhoid fever) and mainly exists in the food and drinking water polluted by the patients’ stool and urine. In this study, the DNA reads was extracted from the patients’ stool and sequenced by Ion Torrent. The sample name is BD1380. The DNA reads is then assembled by using the default parameter settings of GSde novoassembler (Newbler, Roche/454 Life Sciences). The statistics of the DNA reads and assembly results are shown in Table 1.

Table 1: Statistics DNA reads and assembly results
2.2 Reference Genome
We experimentally verified that theSalmonellastrain of BD1380 should belong to a new strain which we called artificial CT18. Artificial CT18 was formed by another sequence called island5 (~20.5k bps) which was inserted in the position 1690319 of S. Typhi strain CT18 chromosome with repeat sequence “CAACATGTA” was at island5 both ends. Therefore, we manually created artificial CT18 and took as the reference genome.
2.3 Pheromone Trail-Based Genetic Algorithm
Zhaoet al.proposed a pheromone trail-based genetic algorithm (PGA) to search globally for the optimal placement for each contig[19]. They have demonstrated that PGA significantly outperforms previous methods, such as Projector2, OSLay, and other BLAST end-based tools. For more details of PGA, please refer to their paper[19].
2.4 Family Competition Genetic Algorithm
The family competition strategy which was first introduced in Yanget al.’s paper[23]in 1997 demonstrated the ability of improving the function optimization problems[22]. The major procedure of the family competition is generating more than one child in each generation. Next, the best one is selected from these offspring as the representative. For more detail, please refer to Yanget al.’s paper[22],[23]. In the family competition strategy, the family competition length (L) is an important parameter that determines the number of offspring generated. In this paper, the length is arbitrarily set to 3 for all test problems.
2.5 Crossover and Mutation
In this paper, we compare three crossovers and two mutations. Three crossovers are cross2[19], order crossover (OX)[24], and partially mapped crossover (PMX)[25]. The two mutations are mutation3 (including 3-exchange mutation and 2-opt[26]) and local search (including reciprocal exchange mutation and shift mutation). The 3-exchange mutation randomly selects two points in the chromosome (three sections are created), and then exchanges the places of these sections. Obviously, there are in total six possible combinations including the offspring itself, then, the best feasible one will be selected as the result of mutation. The reciprocal exchange mutation swaps two randomly chosen genes in the chromosome. The shift mutation inserts a randomly chosen gene into the right of another randomly chosen gene. The reciprocal exchange mutation and the shift mutation would be applied only if the generated offspring is better.
2.6 Fitness Calculation
We adopted the identical fitness calculation as Zhaoet al.’s paper[19], including all parameter settings and function formulas.
3. Result and Discussion
3.1 Results by Using mutation3 and Localsearch
We compare three crossovers combined with three mutations (including using both mutations), so there are in total nine methods. For each method, two versions of the genetic algorithm are used, which are PGA and FCPGA.
The results are shown in Table 2. The parameters are listed in the footnote of the table, including population size, crossover rate (pc), mutation rate (pm), and the number of generation. As shown in Table 2, we find that smaller fitness is obtained when using both mutation3 and localsearch. In this study, smaller fitness implies better performance. The conclusion that applying both mutation3 and localsearch produces better result is consistent throughout this study. In addition, while comparing the results of using PGA and FCPGA, we find that better results are obtained when using FCPGA. Table 3 shows similar results as Table 2; the only difference is the mutation rate changes from 0.001 to 0.01.
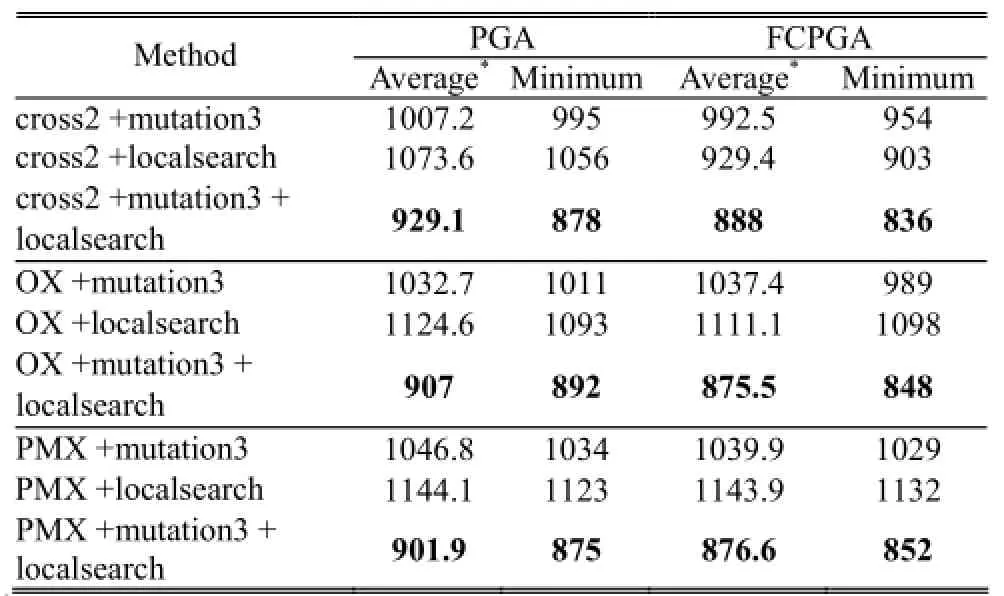
Table 2: Comparisons of average and minimum fitness usingdifferent methods (mutation rate = 0.001)

Table 3: Comparisons of average and minimum fitness usingdifferent methods (mutation rate = 0.01)
3.2 Fitness Comparison between FCPGA and PGA
To investigate the performance of PGA and FCPGA more deeply, we further evaluate their results by using different mutation and crossover rates. As shown in Table 4, there are in total six mutation rates used in this study. Almost all mutation rates demonstrate that FCPGA produces better results than PGA, except for mutation rates are 0.004 and 0.006. Closer inspection reveals that these two mutation rates produce extremely low fitness (797) by accident; therefore lower average fitness is obtained. The second low fitness for mutation rates 0.004 and 0.006 is 854 and 866, respectively; both of them are larger than the average (853.8 and 859.6). Among all mutation rates, our results show that using FCPGA withpm= 0.01 obtains the best result. We then fix the mutation rate (0.01) and evaluate the performance of different crossover rates. As shown in Table 5, there are also six crossover rates used in this study. Similar to the results in Table 4, almost all crossover rates show that FCPGA is better than PGA, except forpc= 0.5. Note that by usingpc= 0.8, FCPGA and PGA produce similar average fitness (861 and 860.8).

Table 4: Average and minimum fitness of using different mutation rates

Table 5: Average and minimum fitness of using different crossover rates
The results demonstrate that our proposed method (FCPGA) produces smaller fitness than PGA, which means better assembly results. The results are consistent by using different combination of mutation and crossover rates. Next, we examine the run time of FCPGA compared to PGA.
3.3 Run Time Comparison between FCPGA and PGA
FCPGA and PGA were run by using one core of a server, equipped with two 2.33 GHz Intel Xeon Quad-Core 5345 Processors with 32 GB RAM. Different combinations of parameters are examined in this study. We calculate the run time of four major operators in genetic algorithm; they are selection, crossover, mutation, and evaluation. The total time is list in the final column of Table 6. As seen from the table, the evaluation takes the longest run time when using PGA; for FCPGA, the most time-consuming operator is crossover. It is strange that PGA with population size 1000 takes extremely long time in the evaluation operator (first two rows in Table 6). We conclude that FCPGA takes shorter run time than PGA under all parameter settings. Due to the number of contig is small, the compute loading of FCPGA is low. Note that we also find that FCPGA produces smaller fitness (better results) than PGA.

Table 6: Run time of each genetic algorithm operator by using different parameter settings
4. Conclusions
Pheromone trail-based genetic algorithm (PGA) has been demonstrated the improvement in genome assembly over previous methods, such as Projector2, OSLay, and other BLAST end-based tools. In this paper, we have developed an extended version of PGA by integrating the family competition mechanism into PGA, called the family competition pheromone genetic algorithm (FCPGA). Our results show that FCPGA performs better than PGA in fitness calculation as well as run time estimation in the real dataset. The family competition length is set to 3 by empirical; however, we may produce better results by testing different lengths. Furthermore, there are still many parameters could be used in the family competition strategy for evaluating its performance, which are omitted in this paper. We firmly believe that better results could be obtained by exploring the family competition more extensively.
Acknowledgment
The authors are grateful to all the members of the Third Branch Office, Center for Disease Control, Taichung.
[1] M. Margulies, M. Egholm, W. E. Altman,et al., “Genome sequencing in microfabricated high-density picolitre reactors,”Nature, vol. 437, pp. 376-380, Sep. 2005.
[2] E. W. Myers, G. G. Sutton, A. L. Delcher,et al., “A whole-genome assembly of drosophila,”Science, vol. 287, pp. 2196-2204, Mar. 2000.
[3] D. R. Zerbino and E. Birney, “Velvet: algorithms for de novo short read assembly using de Bruijn graphs,”Genome Res., vol. 18, pp. 821-829, May 2008.
[4] J. T. Simpson, K. Wong, S. D. Jackman, J. E. Schein, S. J. Jones, and I. Birol, “ABySS: a parallel assembler for short read sequence data,”Genome Res., vol. 19, pp. 1117-1123, Jun. 2009.
[5] J. Butler, I. MacCallum, M. Kleber,et al., “ALLPATHS: de novo assembly of whole-genome shotgun microreads,”Genome Res., vol. 18, pp. 810-820, May 2008.
[6] I. Maccallum, D. Przybylski, S. Gnerre,et al., “ALLPATHS 2: Small genomes assembled accurately and with high continuity from short paired reads,”Genome Biol., vol. 10, pp. R103, Oct. 2009.
[7] R. Li, H. Zhu, J. Ruan,et al., “De novo assembly of human genomes with massively parallel short read sequencing,”Genome Res., vol. 20, pp. 265-272, Feb. 2009.
[8] M. H. Schulz, D. R. Zerbino, M. Vingron, and E. Birney,“Oases: robust de novo RNA-seq assembly across the dynamic range of expression levels,”Bioinformatics, vol. 28, pp. 1086-1092, Apr. 2012.
[9] M. G. Grabherr, B. J. Haas, M. Yassour,et al., “Full-length transcriptome assembly from RNA-Seq data without a reference genome,”Nat. Biotechnol, vol. 29, pp. 644-652, Jul. 2011.
[10] H. T. Chu, W. W. Hsiao, J. C. Chen,et al., “EBARDenovo: highly accurate de novo assembly of RNA-Seq with efficient chimera-detection,”Bioinformatics, vol. 29, pp. 1004-1010, Apr. 2013.
[11] J. R. Miller, S. Koren, and G. Sutton, “Assembly algorithms for next-generation sequencing data,”Genomics, vol. 95, pp. 315-27, Jun. 2010.
[12] M. C. Schatz, A. L. Delcher, and S. L. Salzberg, “Assembly of large genomes using second-generation sequencing,”Genome Res., vol. 20, pp. 1165-1173, Sep. 2010.
[13] M. Baker, “De novo genome assembly: what every biologist should know,”Nature Methods, vol. 9, no. 4, pp. 333-337, 2012.
[14] J. A. Martin and Z. Wang, “Next-generation transcriptome assembly,”Nat. Rev. Genet., vol. 12, pp. 671-682, Oct. 2011.
[15] S. A. van Hijum, A. L. Zomer, O. P. Kuipers, and J. Kok,“Projector 2: Contig mapping for efficient gap-closure of prokaryotic genome sequence assemblies,”Nucleic Acids Res., vol. 33, pp. W560-566, Jul. 2005.
[16] D. C. Richter, S. C. Schuster, and D. H. Huson, “OSLay: optimal syntenic layout of unfinished assemblies,”Bioinformatics, vol. 23, pp. 1573-1579, Jul. 2007.
[17] M. Pop, A. Phillippy, A. L. Delcher, and S. L. Salzberg,“Comparative genome assembly,”Briefings in Bioinformatics, vol. 5, pp. 237-248, Sep. 2004.
[18] P. Husemann and J. Stoye, “Phylogenetic comparative assembly,”Algorithms Mol. Biol., vol. 5, pp. 3, Jan. 2010.
[19] F. Zhao, T. Li, and D. A. Bryant, “A new pheromone trail-based genetic algorithm for comparative genome assembly,”Nucleic Acids Res., vol. 36, pp. 3455-3462, Jun. 2008.
[20] W. J. Kent, “BLAT--the BLAST-like alignment tool,”Genome Res., vol. 12, pp. 656-664, Apr. 2002.
[21] S. Kurtz, A. Phillippy, A. L. Delcher,et al., “Versatile and open software for comparing large genomes,”Genome Biol., vol. 5, no. 2, pp. R12, 2004.
[22] J.-M. Yang and C.-Y. Kao, “Integrating adaptive mutations and family competition into genetic algorithms as function optimizer,”Soft Computing, vol. 4, no. 1, pp. 89-102, 2000.
[23] J.-M. Yang, Y.-P. Chen, J.-T. Horng, and C.-Y. Kao,“Applying family competition to evolution strategies for constrained optimization,”Lecture Notes in Computer Science, vol. 1213, pp. 201-211, Jun. 1997.
[24] I. Oliver, D. Smith, and J. R. Holland, “A study of permutation crossover operators on the traveling salesman problem,” inProc. of the Second Int. Conf. on Genetic Algorithms on Genetic Algorithms and Their Application, 1987, pp. 224-230.
[25] D. Goldberg and R. Lingle, “Alleles, loci and the traveling salesman problem,” inProc. of the First Int. Conf. on Genetic Algorithms and Their Applications, 1985, pp. 154-159.
[26] G. A. Croes, “A method for solving traveling-salesman problems,”Operations Research, vol. 6, no. 6, pp. 791-812, 1958.

Chien-Hao Su received the Ph.D. degree in 2013 from the Department of Computer Science and Information Engineering, National Taiwan University, Taipei. He is now a postdoctoral fellow at the Biodiversity Research Center, Academia Sinica. Currently, he is working on developing a novel method for genome assembly. His research interests include bioinformatics, evolutionary algorithm, metagenomics, and genome assembly.

Chien-Shun Chiou received the Ph.D. degree in 1994 from the Department of Botany and Plant Pathology, Michigan State University, USA. He is a principal investigator at the Center for Research, Diagnostics and Vaccine Development, Centers for Disease Control, Taichung.

Jung-Che Kuo received the M.S. degree in 2012 from the Institute of Biotechnology, National Cheng Kung University, Taichung. He is a member of the research faculty fellow at the Center for Research, Diagnostics and Vaccine Development, Centers for Disease Control, Taichung.
Pei-Jen Wang received the Ph.D. degree in 2010 from the Life Sciences Department, National Chung-Hsing University, Taichung. He is a postdoctoral fellow at the Center for Research, Diagnostics and Vaccine Development, Centers for Disease Control, Taichung. (photograph not available at the time of publication)
Cheng-Yan Kao received the Ph.D. degree in 1981 from the Department of Computer Science, University of Wisconsin-Madison, Madison. He is now a professor with the Department of Computer Science and Information Engineering, National Taiwan University, Taipei. (photograph not available at the time of publication)

Hsueh-Ting Chu received the Ph.D. degree in 2002 from the Department of Computer Science, National Tsing Hwa University, Hsinchu. He then joined the Department of Computer Science and Information Engineering, Asia University, Taichung.
Pei-Jen Wang’s and Cheng-Yan Kao’s photographs are not available at the time of publication.
Manuscript received December 15, 2013; revised March 15, 2014.
C.-H. Su is with the Biodiversity Research Center, Academia Sinica, Taipei (e-mail: chienhao@gmail.com).
C.-S. Chiou, J.-C. Kuo, and P.-J. Wang are with the Center for Research, Diagnostics and Vaccine Development, Centers for Disease Control, Taichung (e-mail: nipmcsc@cdc.gov.tw).
C.-Y. Kao is with the Department of Computer Science and Information Engineering, National Taiwan University, Taipei (e-mail: cykao@csie.ntu.edu.tw).
H.-T. Chu is with the Department of Computer Science and Information Engineering, Asia University, Taichung (Corresponding author: e-mail: htchu@asia.edu.tw).
Digital Object Identifier: 10.3969/j.issn.1674-862X.2014.04.012
杂志排行
Journal of Electronic Science and Technology的其它文章
- Study on Temperature Distribution of Specimens Tested on the Gleeble 3800 at Hot Forming Conditions
- Non-Linearity of Visual Sensitivity and Pursuit Velocity during Smooth Pursuit Eye Movements
- Automatic Vessel Segmentation on Retinal Images
- Quantification of Cranial Asymmetry in Infants by Facial Feature Extraction
- Intrinsic Limits of Electron Mobility inModulation-Doped AlGaN/GaN 2D Electron Gas by Phonon Scattering
- Real-Time Hand Motion Parameter Estimation with Feature Point Detection Using Kinect
