各向异性边缘检测导引的CT稀疏角度重建

戎军艳，刘文磊，高 鹏，廖琪梅，卢虹冰

各向异性边缘检测导引的CT稀疏角度重建

戎军艳，刘文磊，高 鹏，廖琪梅，卢虹冰

目的：提出一种CT稀疏角度重建方法，用以降低CT的辐射剂量。方法：基于图像各向异性的边缘检测信息，在图像重建过程中更新图像总变差各加权分量的加权权重，然后采用图像总变差最小化方法重建图像。结果：计算机模拟结果表明，与传统的总变差最小化方法相比，该方法可以更好地重建图像边缘，且边缘检测的结果会影响重建效果。结论：采用该方法可以增强图像边缘，提高重建图像的分辨率，改善重建图像的质量。

各向异性；边缘检测；总变差最小化；稀疏角度

0 引言

医学研究表明，X线对人体有损伤，电离辐射可从分子和细胞水平对生物体造成损伤，照射X光可诱发癌症、白血病或其他遗传性疾病，因此，降低X线的辐射剂量对CT的临床应用具有重要的意义[1]。降低辐射剂量常用的方法有基于硬件改进的方法、基于条件优化的方法和基于算法改进的方法[2]。在不改变硬件配置的条件下，减少投影角度是一种直接而有效的降低辐射剂量的方法。然而，减少投影角度会导致数据量小，图像重建不能满足Tuy-Smith数据完备性条件[3-4]。传统的滤波反投影（filtered back-projection，FBP）类重建方法导致重建图像分辨率下降、噪声大、条形伪影严重[5]，不再适用。近几年，利用信号的稀疏化将CT稀疏角度重建转化为求解约束或无约束的目标函数的最优化问题的算法取得了显著成果[6-8]。Sidky等[6-7]提出的凸集投影（projection onto convex sets）-总变差（total variation，TV）最小化（简称TV-POCS）方法采用梯度变换计算图像的总变差，利用梯度下降法求解使得总变差最小化的重建图像。TV-POCS方法用于离散扇束和锥束CT重建，结果显示其相对于常用的最大似然-期望最大化方法（maximum likelihood expectation maximization，MLEM）与代数迭代法（algebraic reconstruction technique，ART）可得到更满意的重建图像。但是，该方法在计算图像总变差时采用图像像素梯度向量的模相加得到，未考虑图像梯度的方向性，因此，在图像求解过程中不可避免地带来图像边缘的模糊和分辨率的下降。本文基于此方法，提出图像各向异性边缘检测导引（anisotropic edge guided）的各向异性加权的TV最小化重建方法（简称Aniso-EGTV），采用各向异性加权的图像总变差计算方法，利用图像边缘检测信息更新权重，在一定程度上可提高图像的分辨率。

1 算法原理

1.1 CT成像模型和TV-POCS重建方法

在迭代类重建算法中，通常将CT成像模型离散化。对于离散CT成像系统，其投影可用式（1）表示：

其中，p→为投影向量；M为投影矩阵，描述每个图像像素点对各个探测器单元的贡献权重；为待重建图像，图像上每个像素点用ui，j（i，j∈[0，L-1]）表示，图像大小为L×L。

TV-POCS方法可表示为式（2）所描述的最优化问题，即求满足投影方程且使得图像总变差最小化的u→。图像的总变差用式（3）表示。可以看出，该方法采用图像像素梯度向量的模相加计算图像的总变差，而梯度向量的模为图像像素沿x和y 2个方向的一阶导数（即梯度的分量）的平方和相加后的平方根，其在x和y方向的一阶导数的权重因子是相同的（即各向同性），均为1。未考虑图像梯度的方向性，因此，在图像求解过程中不可避免地带来图像边缘的模糊和分辨率的下降。

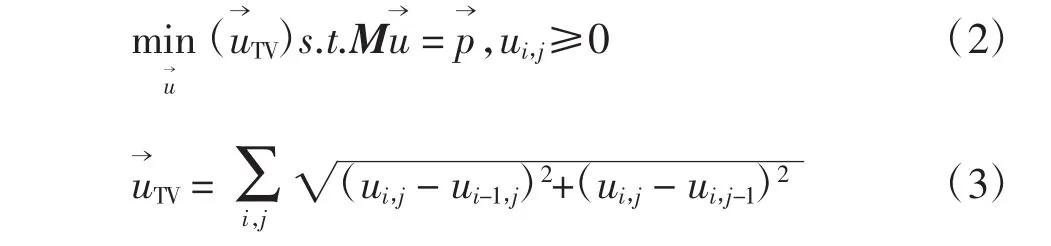
1.2 Aniso-EGTV重建方法

将图像总变差采用式（4）中各向异性加权的方式表达，gα代表中各个分量的权重因子，Dα表示对图像取变分操作，表示像素（i，j）与其邻域（k，l）变分的权重。计算中分量的个数由像素点的邻域α决定，具体用N（l，j）表示像素（l，j）的邻域，在此我们采用四邻域计算。由此，类似于TVPOCS方法，各向异性加权的TV最小化方法用式（5）表示。

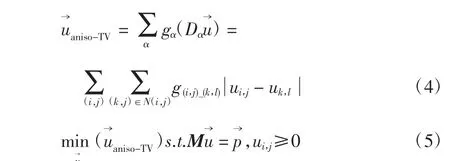
1.2.1 权重的更新

在四邻域中，权重初始值设为π/4，我们将权重因子g构造为L×L×4的三维矩阵，计算u→aniso-TV时每个像素点有4个权重因子与其对应。权重随着图像迭代求解过程不断更新，更新方法为：对选择的图像进行边缘检测，当图像像素位于边缘时将权重设为零，否则保持不变。

1.2.2 边缘检测方法

为了满足权重因子的更新规则，我们改进了传统的Canny检测方法[9]，提出各向异性的Canny边缘检测方法。具体过程如下：

（1）对图像进行高斯滤波。

（2）对滤波后的图像分别沿x、y方向求导，得到对应的梯度分量图像Dx与Dy。

（3）沿梯度方向对滤波后的图像进行梯度模的非极大值抑制，确定梯度模的局部最大值点位置。

（4）对步骤（3）找到的梯度模的局部最大值点的梯度模进行高、低双阈值约束，从而找到大于等于高阈值的点域Ω和位于高、低阈值之间的点域Ψ。

（5）根据梯度分量图像Dx与Dy将图像像素点（i，j）按照其梯度矢量所属区域分为x向边缘点以及y向边缘点。x向边缘指边缘切线方向偏向x轴，y向边缘指边缘切线方向偏向y轴。

（6）分别针对x向边缘和y向边缘，对Ω中的点以Ψ中的点作为连通邻域补充进行形态学连接和边缘细化。

由此可得到沿x方向和y方向的2幅边缘图像，可利用这2幅边缘图像进行上节中权重的更新。

1.2.3 Aniso-EGTV算法流程

参考TV-POCS算法，总结Aniso-EGTV流程如图1所示，具体如下：

（1）设置初始迭代次数k=0，初始化重建图像u（0），图像大小为L×L；同时，初始化图像总变差计算中用于各向异性加权的权重矩阵g，权重因子初始值均设为1。

（2）增加迭代次数k=k+ 1，利用代数迭代法重建得到更新的重建图像u（k）。

（3）根据步骤（2）中得到的更新的重建图像，求解满足图像总变差最小化的图像。

（4）对选择的图像进行各向异性的边缘检测，得到x和y 2个方向的边缘图像Ex以及Ey。

（5）根据边缘图像更新权重矩阵为gnew。

（6）使用更新后的权重矩阵计算图像的图像总变差。

重复步骤（2）～（6）直至满足迭代截止条件，并输出图像。

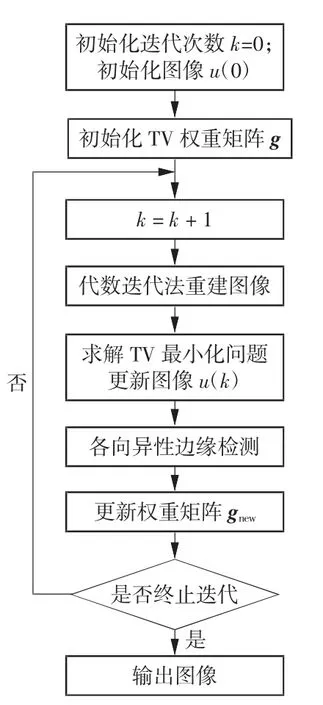
图1 Aniso-EGTV算法流程图

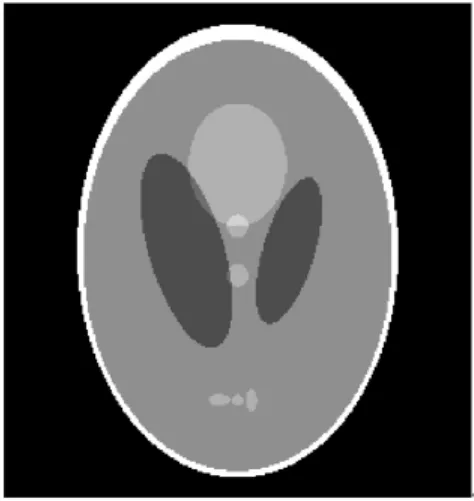
图2 Shepp-Logan理想图像（true）

2 结果

对Shepp-Logan理想模型离散为256×256的矩阵（记为true，如图2所示）后进行等距扇形束投影，射线源到探测器的距离为800 mm，到旋转中心的距离为400mm。探测器像素大小为0.806 6 mm，共有512个像素。360°扫描范围内均匀产生360幅投影，从投影中分别均匀抽取15、20、40个角度的投影数据，在无噪或添加高斯噪声情况下进行重建。

首先采用重建图像做边缘检测，利用边缘检测结果做权重的更新，重建图像如图3的中间列所示，记作Aniso-EGTV-Mid。为了更好地得到边缘信息，采用理想图像做边缘检测，重建结果如图3的最后一列所示，记作Aniso-EGTV-Prior。为了比较不同算法的重建效果，将采用TV-POCS方法重建的结果列于图3第一列。同时，为了更好地观察，放大虚线方框中感兴趣区置于各图的右下角。图4画出了各个稀疏角度下重建图像第205行的剖线图，可以看到Aniso-EGTV方法重建的结果与理想图像更为接近，可以更好地恢复图像的边缘。

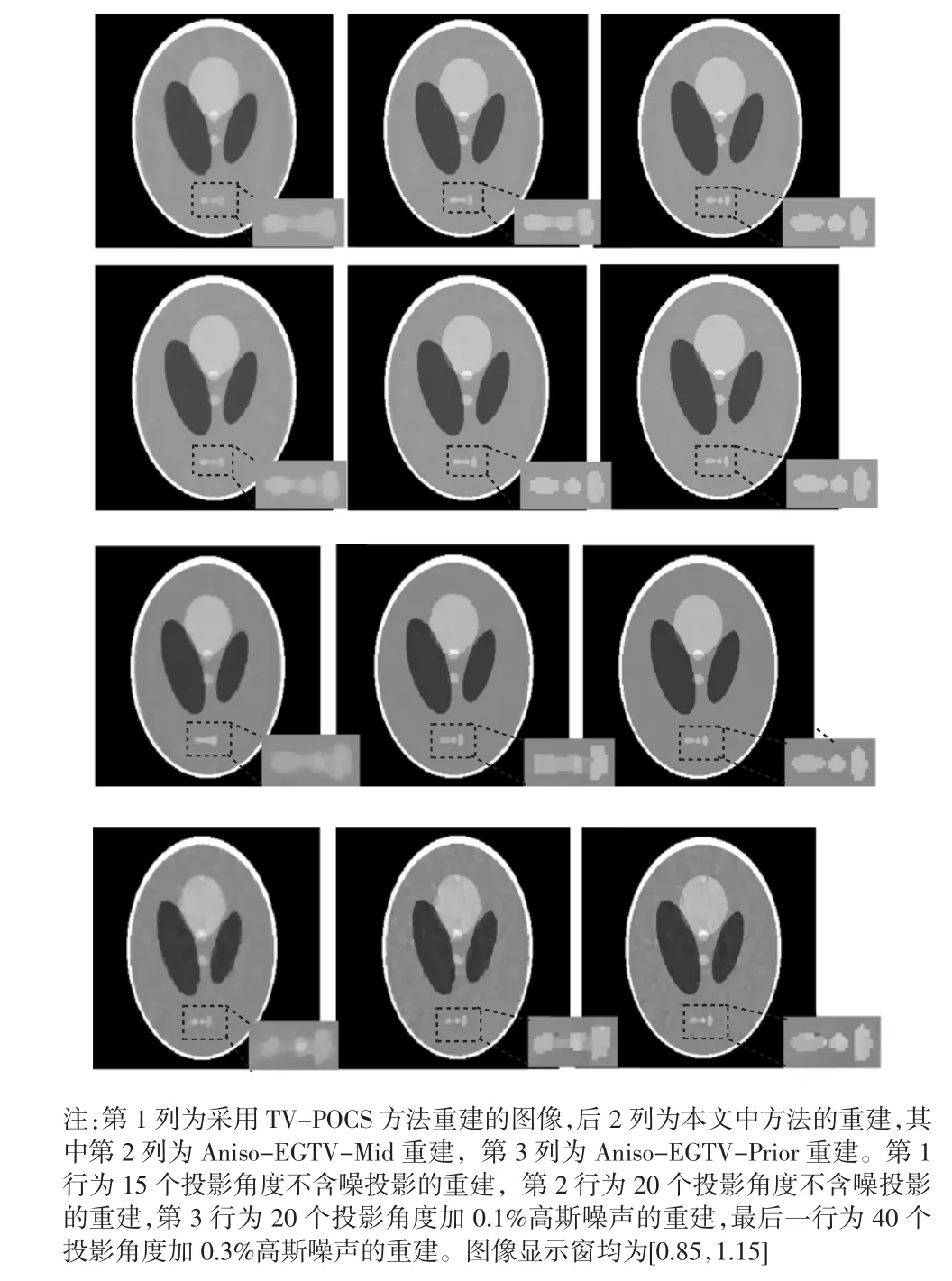
图3 采用不同方法重建的图像

3 讨论

利用图像梯度变换的稀疏化信息可以在较少的角度下重建CT图像，且稀疏化模型直接影响着重建图像的质量。相比于传统的TV-POCS方法，本文提出的Aniso-EGTV算法基于图像各向异性的边缘检测信息更新TV计算中各分量的权重，用于后续的最优化计算过程，从而实现各向异性的TV最小化重建方法。该方法可以更好地保持图像边缘的分辨率，重建结果与真实图像更为接近。

图4 采用不同方法重建的图像第205行的剖线图

Aniso-EGTV算法的重建效果依赖于边缘检测的精度，利用理想图像边缘检测的结果重建时能够减少由于数据不完全和噪声导致的图像变形。因此，好的边缘检测方法或者一些有关图像边缘的先验信息更有利于该方法的实施。但是好的边缘检测方法往往带来参数选择的困难，增加算法的复杂度。因此，实际中需要权衡边缘检测算法的实用性、复杂度、精度等之间的利害关系，选择合适的边缘检测算法。

[1]Brenner D，Hall E.Computed tomography—an increasing source of radiation exposure[J].The New England Journal of Medicine，2007，

（▶▶▶▶）（◀◀◀◀）357（22）：2 277-2 284.

[2]Kalender W.Dose in x-ray computed tomography[J].Phys Med Biol，2014，59：R129-R150.

[3]Tuy H.An inverse formula for cone-beam reconstruction[J].SIAM J Appl Math，1983，43：546-552.

[4]Smith B.Image reconstruction from cone-beam projection：necessary and sufficient conditions and reconstruction methods[J].IEEE Trans Med Imaging，1985，4（1）：14-25.

[5]LIU Y，MA J，FAN Y，et al.Adaptive-weighted total variation minimization for sparse data toward low-dose x-ray computed tomography image reconstruction[J].Phys Med Biol，2012，57（23）：7 923-7 956.

[6]Sidky E Y，Kao C M，Pan X C.Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT[J].Journal of X-Ray Science and Technology，2006，14：119-139.

[7]Sidky E Y，Pan X.Image reconstruction in circular cone-beam computed tomography by constrained，total-variation minimization[J]. Phys Med Biol，2008，53：4 777-4 807.

[8]邹晶，孙艳勤，张朋.由少量投影数据快速重建图像的迭代算法[J].光学学报，2009，29（5）：1 198-2 004.

[9]Canny J.A computational approach to edge detection[J].IEEE Trans Pattern Anal Mach Intell，1986，8（6）：679-698.

（收稿：2014-03-26 修回：2014-06-17）

Anisotropic edge guided CT reconstruction from sparse views

RONG Jun-yan,LIU Wen-lei,GAO Peng,LIAO Qi-mei,LU Hong-bing
(School of Biomedical Engineering,the Fourth Military Medical University,Xi'an 710032,China)

ObjectiveTo develop a reconstruction algorithm for sparse view computed tomography (CT)to decrease the radiation dose.MethodsFirstly,the weights of the adding elements of the image total variation were updated according to the anisotropic edge detection information.Then the total variation minimization(TV minimization)algorithm was implemented to reconstruct the image.ResultsComputer simulation showed that the proposed algorithm could reconstruct the edge area much better than the conventional TV minimization.The precision of edge detection affected the reconstruction results.ConclusionThe proposed algorithm can enhance the image edge and improve the resolution and quality of reconstructed images.[Chinese Medical Equipment Journal，2014，35（10）：4-6，15]

anisotropic;edge detection;TV minimization;sparse view

R318；TH774

A

1003-8868（2014）10-0004-04

10.7687/J.ISSN1003-8868.2014.10.004

国家科技支撑计划课题（2011BAI12B03）；中国博士后科学基金（2012M521863）；国家自然科学基金（81230035）

戎军艳（1981—），女，博士，主要从事低剂量CT成像算法方面的研究工作，E-mail：junyanrong@126.com。

710032西安，第四军医大学生物医学工程学院（戎军艳，刘文磊，高 鹏，廖琪梅，卢虹冰）

卢虹冰，E-mail：luhb@fmmu.edu.cn