一种基于多频电阻抗断层成像系统的校准方法研究

杨 琳，徐灿华，史学涛，付 峰，代 萌，夏军营，李 靖，董秀珍

一种基于多频电阻抗断层成像系统的校准方法研究

杨 琳，徐灿华，史学涛，付 峰，代 萌，夏军营，李 靖，董秀珍

目的：研究一种简便、有效的多频电阻抗断层成像数据采集系统的幅频和相频校准方法，以提高成像数据的质量。方法：基于系统的正交数字解调方法的特点，提出相频和幅频校正方法；通过电阻网络模型和单通道测量实验给出校正因子的获取方法；开展物理模型实验，对比校准前后的数据质量以及成像结果。结果：物理模型实验表明，校准后的数据质量明显得到改善，成像结果能够清晰地反映成像目标。结论：该校准方法是一种简便、有效的多频电阻抗断层成像系统的幅频和相频校准方法，为未来将多频电阻抗成像技术应用于临床奠定了良好的基础。

多频电阻抗成像数据采集系统；幅频；相频；校准方法

0 引言

电阻抗断层成像（electrical impedance tomography，EIT）是一种新型的成像技术，其通过向人体施加安全激励电流（电压），同时测量边界电压（电流），然后利用成像算法计算出目标内阻抗的分布或者变化的图像。由于该技术对人体无害，而且与传统临床成像技术相比，具有无辐射、无创、便携、低成本和功能成像等优势，所以，具有良好的临床应用前景[1]。

目前，大多数的EIT临床应用都是针对不同时刻的阻抗变化进行成像（时差成像），这种成像方式可对疾病的发展过程进行实时动态地监测，但是对于已经存在并在短期内不会发生变化的疾病，例如脑血肿、肿瘤等，则难以达到检测的目的。而相关文献表明，人体的不同组织具有不同的阻抗频谱特性[2－3]，因此，可利用同一时刻不同激励频率下的电阻抗特性的差异进行成像，以期达到诊断疾病的目的，这种EIT成像方式即为多频电阻抗断层成像（multi-frequency electrical impedance tomography，MFEIT）。

MFEIT要求数据采集系统能够工作在较宽的频带范围内，同时，对系统的精度也提出了更高的要求。但是系统内部的器件、电路布线、电极导线等会产生一定的分布电容，而分布电容的电阻抗会随测量频率的改变而变化，因而会不可避免地引入因工作频率的不同而产生的测量误差，这些误差可能导致在成像结果中无法准确地分析成像目标内的阻抗信息，故在实际应用前需要对这种误差进行校准。本文从幅频特性和相频特性2个方面对本课题组自主研发的MFEIT数据采集系统进行了研究，提出了幅频和相频校准方法，并通过物理模型实验对比了校准前后的结果，证明了校准的有效性。

1 材料和方法

1.1 MFEIT系统的测量原理

MFEIT系统的性能为：工作频率为1～190 kHz，输出电流为0～1.25 mA，测量速度为1帧/s，共模抑

制比大于75 dB，互易性误差小于0.11%[4]。本文采用的激励测量模式为对向激励（电流激励）、邻近测量（电压测量）。该系统共16个电极，测量原理如图1所示。某一时刻，某一对相对电极作为激励电极向目标施加电流，其余邻近电极测量电压，每对电极激励下共有12个测量通道的数据有效；下一时刻，另一对相对电极作为激励电极，其余相邻电极测量电压，当遍历完所有电极之后，所有测量电压形成一帧数据（192个）。

图1 MFEIT系统的测量原理

假设激励信号为I=Asin（kωt），幅度为A，角频率为kω，测量信号经每周期的N点均匀采样（N＞2k）后可得序列为：

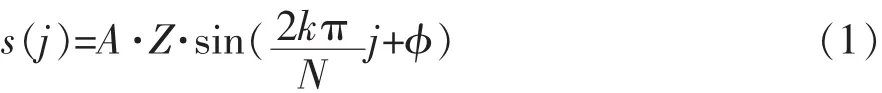
式中，Z为阻抗的模值，φ为相移，j为0～N-1的整数。

采用正交数字解调方法[5]，分别构造正弦序列和则S与 S1和S2的内积分别为：

其中，Re和Im分别对应角频率为ω时阻抗的实部和虚部。

图2 MFEIT测量系统误差来源等效电路图

1.2 相位误差和幅度误差的校准方法

当系统工作在不同频率时，测量数据会受到多方面的影响。图2为MFEIT测量系统误差来源等效电路图，其中Rs和Cs为电流源的输出阻抗，R0和C0为电极与皮肤之间的接触所产生的阻抗，Cd为导线、电子器件（例如多路开关[6]）对地的分布电容，Ri和Ci为电压放大器的输入阻抗，RL和CL为负载。因为系统的各个误差成分复杂，而且随系统的工作频率发生变化，因而无法通过严格的数学推导进行求解[7]，所以，本文采用实验的方法对系统误差进行校准。

在实际应用中，系统误差的影响使相移φ不仅包含了组织引起的相位偏移（φz），而且包含了系统误差引起的相位偏移（ξ），即：φ=φz+ξ；同时，使模值（Z）受到一定程度的偏移，即：Z=μ·Z0，μ为幅值偏移系数。 因此，式（2）、（3）可写为：

理论上，如果不存在系统误差（μ=1，ξ=0），那么，当负载为电阻时，由于负载不会产生相移（φz=0），并且负载上测得的电压信号应只与激励电流（I）和负载（Z0=R）有关，所以，经解调后的阻抗实部和虚部分别为：

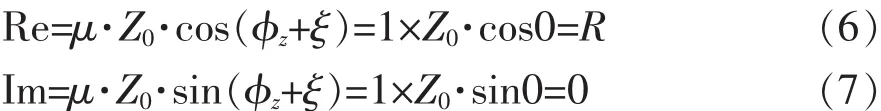
但是，在实际中，由于系统误差的存在，使得不同频率下的测量电压信号具有不同程度的相位偏移和幅值偏移（μ≠1，ξ≠0），所以，经解调后的阻抗实部和虚部具有如下形式：

因此，当负载为电阻（R）时，可通过公式（8）、（9）计算系统在不同频率点上的ξ和μ，即：

计算出ξ和μ后，就可利用ξ和μ校准测量数据，即ξ和μ分别为相频校正因子和幅频校正因子。

1.3 获取系统校正因子

由于系统的互易性误差小于0.11%，所以，可利用单通道测量数据计算校正因子。本文首先采用电阻网络模型验证系统的各通道在各频率点的测量一致性，然后研究单通道不同阻值（正常脑部传输阻抗范围内）的负载在各频率点处的相位偏移和幅值偏移，最后根据不同负载的校正因子确定系统整体的校正因子。

1.3.1 系统各通道的一致性验证

本文采用由精密电阻构成的电阻网络模型，电路图如图3（a）所示。设置激励频率分别为1～10（增量为1 kHz）、20～190 kHz（增量为10 kHz），共计28个频率（以下实验设置相同），激励电流设置为1 000 μA，采集速度为1帧/s，每个频率点共采集100帧数据。

若激励电流频率总数为M=28，每个频率点上的采集帧数N=50，每帧数据为其中，i＝1，2，…，N表示每个频率点的采集帧数，j＝1…M表示频率，k＝1，2，…，192表示每帧数据的通道数，各频率点的各通道测量均值为：由于电阻网络模型的对称性，可将每对电极激励下的12个测量数据分为2组（每组6个数据），而且这2组数据具有对称性，同理，每帧数据中有32组数据具有对称性。基于此，各频率点处的总体测量均值为其中，m＝1，2，…，6。然后计算各频率的数据与总体均值的比率其中，k＝m·n，n＝1，2，…，32。最后以各频率处rj（k）的标准差评价各频率处各通道幅值的一致性误差（amplitude channel consistency error，ACCE），即：ACCEj＝std（rj（1），rj（2），…，rj（k）），其中，std（·）表示·的标准差，并将ACCE的最大值作为系统各通道的一致性误差（system amplitude channel consistencyerror，SACCE），即：SACCE=max（ACCEj），其中，max（·）表示·的最大值。

其中，mean（·）表示·的均值。

1.3.2 系统整体校正因子的确定

电极测量的生物阻抗主要包括接触阻抗和生物阻抗，在低频范围内主要为接触阻抗。接触阻抗随频率的增大而减小，但是仍有较大值。初步的人体实验表明，脑部的传输阻抗为1～70 Ω（32电极法）。当频率为20～256 kHz时，接触阻抗为300 Ω～2.7 kΩ。为了使电流源的工作接近实际情况，在进行实验时需考虑接触阻抗的影响，所以，本文采用的电路如图3（b）所示，选择接触阻抗Zc为500 Ω的电阻。由于课题组采用16电极法，理论上传输阻抗范围应为2～140 Ω。本文在2～140 Ω内选择9个精密电阻作为负载，各电阻的阻值由精密阻抗分析仪（Agilent 4294，Palo Alto，USA）进行测量。系统与电极之间的导线的长度为1 m，采用电极对（1-9）驱动，电极对（2-3）测量负载上的电压，每个频率点采集100帧数据。

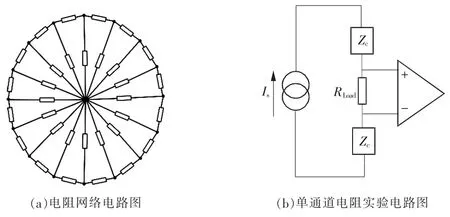
图3 电阻网络和单通道电阻电路图

1.4 验证校准方法

为了验证校准方法的有效性，开展盐溶液物理模型实验和多频电阻抗成像实验。

1.4.1 盐溶液物理模型实验

本实验采用的物理模型是内径为205 mm的半球形有机玻璃容器，容器内壁等间距地安放16个电极。盐溶液的质量分数为0.05%（盐溶液的阻抗频谱特性与电阻相同，测量信号应只具有实部值，且在频带内稳定不变，而虚部值为0），激励电流为750 μA，每个频率点采集100帧数据。

1.4.2 多频电阻抗成像实验

本实验采用1.4.1所述的物理模型，盐溶液的质量分数为0.04%，成像目标为胡萝卜（其阻抗随频率变化），电流的激励频率为750 μA。然后分别对校准前后的2种不同频率下的测量电压的差值进行成像，成像算法采用课题组提出的阻尼最小二乘重构算法[8]，即：

其中，S为敏感性矩阵，λ为正则化参数（文中选择λ= 0.1），R为正则化矩阵

2 结果

2.1 获取系统校正因子

2.1.1 电阻网络的测量结果

从图4（a）可以看出，ACCE在190 kHz处达到

最大值，SACCE＜0.22%。从图4（b）可以看出，PCCE随着频率的升高而增加，在190 kHz处达到最大值，SPCCE＜2%。因此，系统的各通道具有很好的一致性，可通过单通道数据计算校正因子。

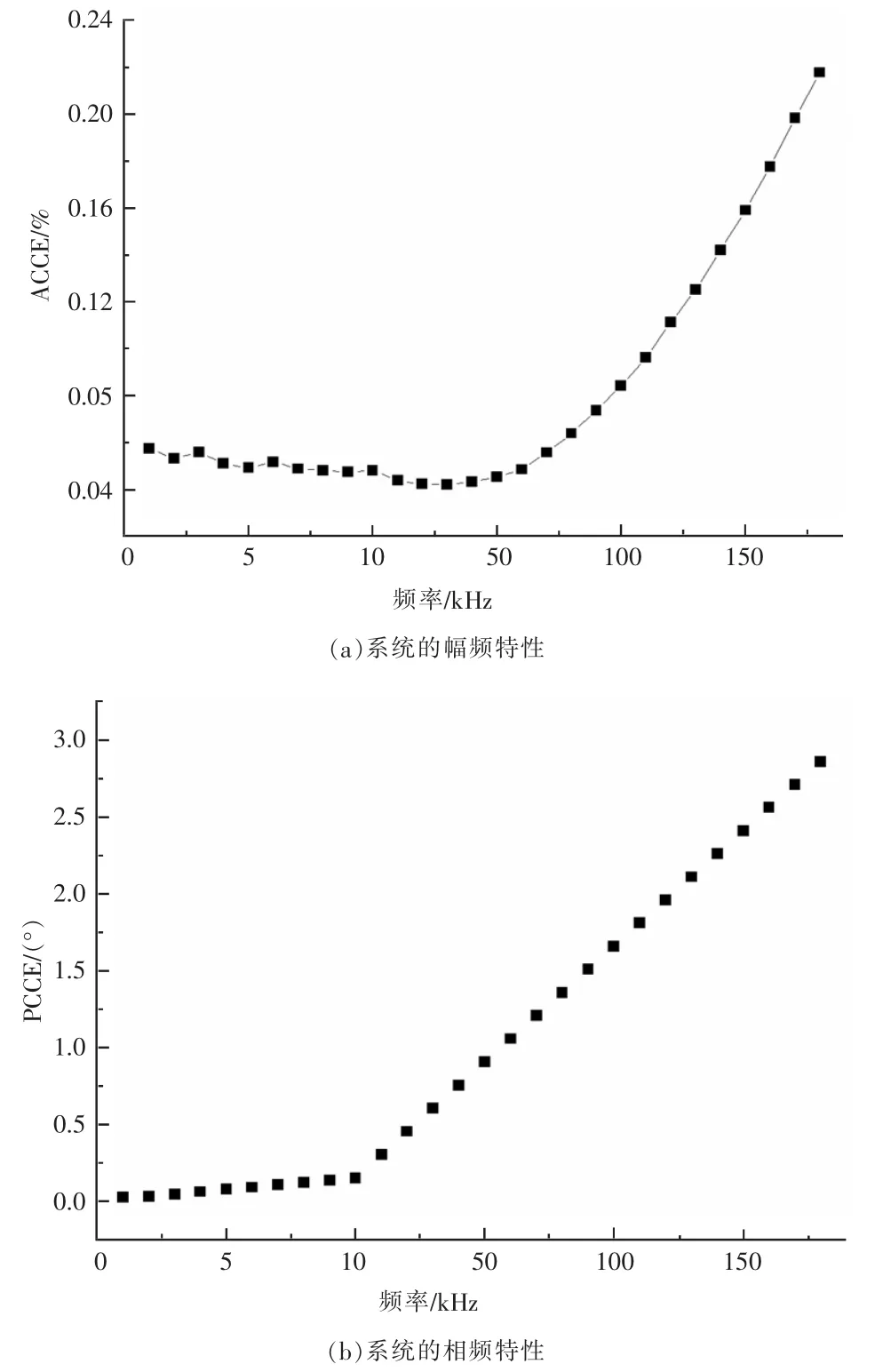
图4 系统的幅频特性和相频特性

2.1.2 单通道不同阻值电阻的测量结果

图5分别是负载为不同阻值的幅频和相频校正因子。从图5（a）中可以看出，不同阻值之间的幅频校正因子的差异（标准差）在190 kHz处达到最大值（0.003 5），但是偏差（标准差/均值）小于0.36%。所以，本文将所有阻值的幅频校正因子的均值作为系统的幅频校正因子。

从图5（b）中可以看出，不同阻值之间的相频校正因子的差异随频率的增加而变大，在190 kHz处达到最大值（1.16°），但是偏差小于0.83%。所以，本文将所有阻值的相频校正因子的均值作为系统的相频校正因子。

2.2 验证校准方法

2.2.1 盐溶液物理模型实验

采用2.1节所获取的幅频校正因子和相频校正因子校准物理模型实验中采集的数据，图6为测量数据校准前后的结果。从图中可以看出，校准前实部和虚部存在负值，其值随频率的改变发生较大变化；校准后，实部值远大于虚部（10倍以上），而且实部数据在频带内变化较小（0.8%以下）。

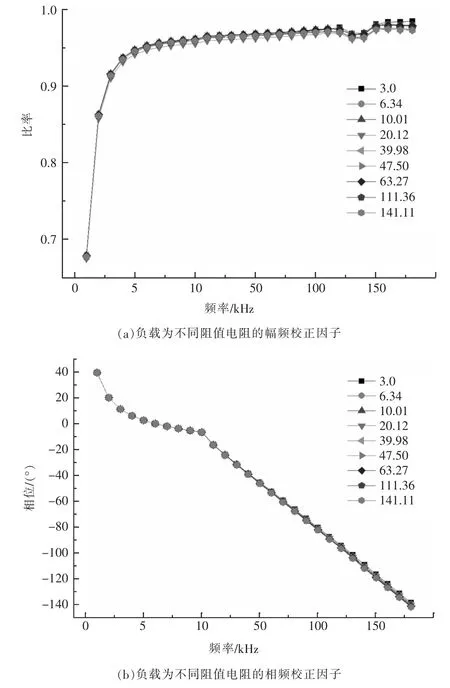
图5 负载为不同阻值电阻的幅频校正因子和相频校正因子

图6 数据校准前后的结果

2.2.2 多频电阻抗成像实验

选择1 kHz和150 kHz的模值和实部数据进行成像，成像结果如图7所示。结果表明，校准前的模值成像结果中虽然可以反映目标，但是存在较多伪

影，实部成像结果中无法对目标进行定位；校准后模值和实部成像结果中的目标清晰，伪影较少，能较好地反映目标信息。

图7 校准前后的成像结果

3 讨论

电阻网络实验结果表明，系统的SACCE和SPCCE都较小，说明系统各通道之间具有很好的一致性，所以，可通过单通道数据计算系统的幅值偏差和相位偏差；从单通道数据结果可以看出：当负载在正常脑部传输阻抗范围内时，不同阻值负载之间的校正因子差别较小。因此，本文将所有负载的校正因子的均值作为系统的校正因子，而在实际中，可通过单通道单一电阻（阻值在正常脑部传输阻抗范围内）对系统进行校准。此研究大大简化了校准过程，同时保证了校准的可靠性。

为了验证校准因子的准确性，本文开展了盐溶液实验。实验结果表明：校准后的数据质量比校准前明显得到改善，实部值在频带内基本稳定。尽管随着频率的升高，虚部值有所增加，但相比实部值较小。校准后的数据的虚部在高频 （＞100 kHz）仍有一定值，产生的原因可能是系统的电极引线和单通道测量实验中的电极引线不同。因此，应考虑一些降低高频误差的方法，例如增加屏蔽或者尽量缩短电极引线[9]。针对与校准实验所用差异（长度、屏蔽层等）较大的电极线，应根据具体的实际测量数据计算校正因子。

在多频成像实验中，校准后的模值图像质量明显优于校准前，证明了幅频校正因子的有效性；校准前的实部图像不能反映目标，而在校准后的图像中，目标清晰，验证了相频校正因子的有效性。在实际中，针对每套系统可预先通过校准方法得到幅频和相频校正因子，并将其存储在计算机内，在以后的应用中可直接利用校正因子对测量数据进行校准。

总之，本文针对MFEIT对硬件采集系统的要求提出了一种简便、有效的系统的幅频特性和相频特性的校准方法，根据实验确定了幅频和相频校正因子，并通过物理模型实验验证了校准方法的有效性，为未来将多频电阻抗成像技术应用于临床奠定了良好的基础。

[1]董秀珍.生物电阻抗成像研究的现状与挑战[J].中国生物医学工程学报，2008，27（5）：641-643.

[2]廖琪梅，徐玉乔，董秀珍，等.乳腺癌及周围组织电阻抗频谱特性与其病理学特征的研究[J].生物医学工程与临床，2008，12（24）：263-266.

[3]Geddes L A，Baker L E.The specific resistance of biological materials：a compendium of data for the biomedical engineer and physiologist[J].Med Biol Eng，1967，5：271-293.

[4]史学涛，尤富生，霍旭阳，等.高精度电阻抗断层成像数据采集系统[J].数据采集与处理，2010，25（2）：256-263.

[5]史学涛，董秀珍，秦明新，等.用于电阻抗多频及参数成像数据采集系统的正交序列解调法[J].第四军医大学学报，2000，21（7）：164-166.

[6]Cook R D，Saulnier G J，Gisser D C，et al.ACT3：A high speed，high precision electrical impedance tomography[J].IEEE Trans Biomedical Engineering，2002，4（8）：713-722.

[7]McEwan A，Cusick G，Holder D S.A review of errors in multi-frequencyEITinstrumentation[J].PhysiolMeas，2007，28：S197-S215.

[8]Canhua Xu，Meng Dai，Fusheng You，et al.An optimized strategy for real-time hemorrhage monitoring with electrical impedance tomography[J].Physiol Meas，2011，32（5）：585-598.

[9]Huaxiang Wang，Chao Wang，Wuliang Yin.Optimum design of the structure of the electrode for a medical EIT system[J].Meas Sci Technol，2001，12：1 020-1 023.

（收稿：2013-06-26）

Calibration Method Based on Multi-frequency Electrical Impedance Tomography System

YANG Lin,XU Can-hua,SHI Xue-tao,FU Feng,DAI Meng,XIA Jun-ying,LI Jing,DONG Xiu-zhen (School of Biomedical Engineering,the Fourth Military Medical University,Xi'an 710032,China)

ObjectiveTo develop a simple and effective method that calibrates amplitude frequency and phase frequency of multi-frequency EIT data acquisition system,so as the quality of imaging data can be improved to lay a solid foundation for multi-frequency EIT.MethodsA calibration method of amplitude frequency and phase frequency was proposed based on the system characterization of orthogonal digital demodulation.Subsequently the method to acquire the calibration factor was given by the experiments of resistor network and single-channel measurement.Finally physical phantom experiments were conducted and data quality as well as image results were contrasted before and after calibration.ResultsThe results of physical phantom experiments showed that after calibration there was a significant improvement of data quality and the imaging target could be clearly reconstructed.ConclusionThis method is simple and effective for calibration of amplitude frequency and phase frequency of multi-frequency EIT system.[Chinese Medical Equipment Journal，2014，35（1）：1-5]

multi-frequency EIT data acquisition system;amplitude frequency;phase frequency;calibration method

R318；R312

A

1003-8868（2014）01-0001-05

10.7687/J.ISSN1003-8868.2014.01.001

国家科技支撑计划课题（2011BAI08B13）；国家自然科学基金课题（51207161）；国家自然科学基金重点项目（50937005）；国家自然科学基金面上项目（61071033）；陕西省自然科学基金课题（2012JQ4012）

杨 琳（1988—），男，硕士研究生，主要研究方向为电阻抗断层成像的算法，E-mail：yanglin.0601@163.com。

710032西安，第四军医大学生物医学工程学院（杨 琳，徐灿华，史学涛，付 峰，代 萌，夏军营，李 靖，董秀珍）

董秀珍，E-mail：dongyang@fmmu.edu.cn