基于MATLAB的MCM对GUM不确定度框架验证

杨图强

（三明市计量所，福建 三明 365000）

1 引言

ISO/IEC GUIDE 98-3：2008《 测 量 不 确定度 第3部分：测量不确定度表示指南》（Uncertainty of measurement-part 3：Guide to the expression of uncertainty in measurement），简称GUM。我国在这一最新国际标准和贯彻JJF1059-1999的基础上，修订并发布实施了JJF1059.1-2012。在日常的不确定度评定中，GUM为主要的评定方法。GUM通过建立输出量是输入量的函数关系这一测量模型，应用不确定传播率传播输入量的最佳估计值和其相关的标准不确定度获得输出量的估计值及其不确定度。但GUM应用有一定的局限性和假设条件，仅当假设输入量的概率分布呈对称分布或近似为正态分布、t分布[1]；测量模型为线性模型、可转换为线性模型或可用线性模型近似的模型时方可采用GUM进行评定。

蒙特卡洛法(Monte Carlo Method)简称MCM，与GUM不同，其评定测量不确定度中，应用分布传播的方式，使用建模阶段所提供的信息来确定输出量的概率密度函数（PDF）。输出量的概率密度函数（PDF）用于获取输出量的估计、标准不确定度以及给定包含概率下输出量的包含区间。MCM尤其适用于不宜对测量模型进行线性化等近似场合以及输出量的概率密度函数（PDF）较大程度地偏离正态分布或t分布这两种情况。2013年6月21日起实施的JJF1059.2-2012《用蒙特卡洛法评定测量不确定度》（Monte Carlo Method for Evaluation of Measurement Uncertainty）指出MCM的适用范围比GUM更广泛，且可用MCM对GUM不确定度框架进行验证，并评价GUM评定的结果。

文中以动平衡机不平衡量校准中示值的测量不确定度评定为例，运用常规的GUM进行不确定度评定，再通过MCM对GUM的不确定度框架进行验证。结合实例的理论阐述，能给读者在不确定度框架验证中提供参考和帮助，较快地掌握不确定度框架的验证方法，具有一定的现实意义。

2 验证方法及步骤

2.1 验证方法

JJF1059.2-2012规定采用MCM对GUM不确定度框架验证时采用自适应蒙特卡洛法。自适应蒙特卡洛法（MCM）的计算算法在JJF1059.2-2012的4.8.4节中已有详细阐述，在此不做赘述。

2.2 验证步骤

（1）运用GUM不确定度框架得到输出量

（2）运用蒙特卡洛法获得输出量估计值相关的标准不确定度u(y)以及包含区间的端点值y_low和 y_high；

（3）确定数值容差δ；

（4）通过公式计算

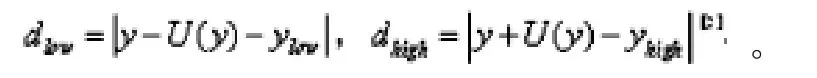
3 验证实例——GUM法

3.1 数学模型

依据JJF1151-2006《车轮动平衡机校准规范》，以AT-7010型车轮动平衡机现场校准为例，动平衡校准示值不确定度的测量模型为：

3.2 灵敏系数

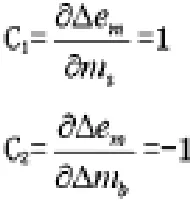
3.3 标准不确定度评定

3.3.1 试重标称值引入的标准不确定度

试重在使用中按标称值使用，标称值以g为单位，其所引起的极限误差为0.5g,分布为均匀分布，包含因子,所以其引入的标准不确定度

3.3.2 被检车轮动平衡机不平衡量示值引入的

标准不确定度

该型被检车轮动平衡机不平衡量示值分度值为5g，其所引起的极限误差为2.5g,分布为均匀分布，包含因子，所以其引入的标准不确定度。

3.3.3 被检车轮动平衡机不平衡量示值重复性引入的标准不确定度

用一试重为120g的砝码，对车轮动平衡机做10次动平衡测试，车轮动平衡机的不平衡质量示值显示如下：120g, 120g, 125g, 120g, 120g,120g, 120g, 120g, 120g, 120g。

3.4 合成标准不确定度

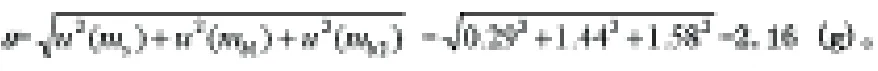
3.5 扩展不确定度

则该车轮动平衡机示值测量修正值的扩展不确定度为4.2g，k=1.96。

4 验证实例——MCM法

4.1 数学模型

该例中，用加载试重测试的方式测量不平衡量，属于直接测量，因此数学模型为f=X。此时应考虑，试重自身的误差以及数显分辨力对测量结果会产生影响，应将这些影响补充到数学模型中，则数学模型变为：

4.2 输入量PDF设定

表1 输入量及概率密度函数PDF

4.3 蒙特卡洛模拟次数

4.4 数值容差δ

测量不确定度取两位有效数字，ndig=2， =-1；因此数值容差δ=1/2×10-1=0.05。自适应蒙特卡洛法建议采用数值容差为δ/5的结果，则该实例在自适应蒙特卡洛法中实际使用的数值容差为0.01[4]。

4.5 MCM程序

MCM程序通过以下步骤实现概率分布传播和不确定度评定。

首先，定义MCM的输入，选择合适的蒙特卡洛实验次数M，确定与输出量相关的输入量的数学模型，并为其设定PDF(如正态分布、矩形分布等)；

其次，将MCM进行传播，从输入量的PDF中抽取M个样本值，对每个样本值进行计算，得出输出量的模型值；

最后，获得MCM的输出，将获得的输出量模型值进行递增次序排列，得出输出量的分布函数的离散表示G，由该离散表示G计算估计值、标准偏差以及在给定包含概率p时的包含区间[2]。

MCM程序流程图如下图1所示。

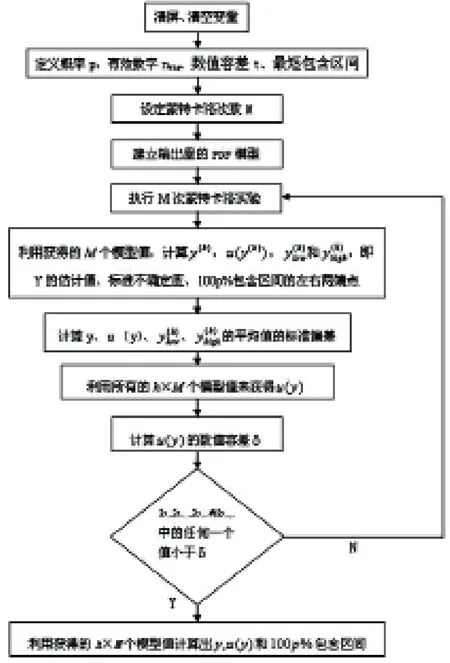
图1 MCM程序流程图

MCM的matlab程序如下：

5 验证

运行以上MATLAB程序得出各参数值如下表2所示。

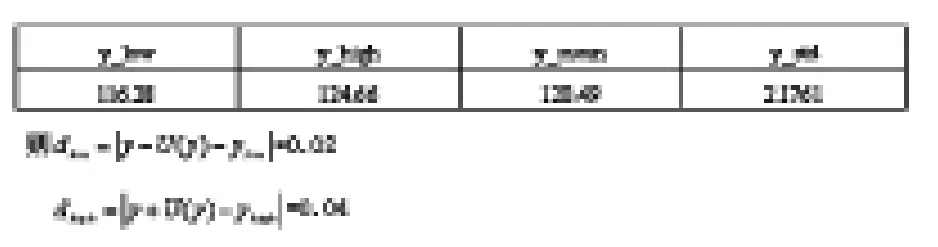
表2 MATLAB运行结果

将GUM的计算结果与MCM运行结果汇总如下表3所示。

表3 GUM/MCM的最终结果

由以上数据得出，MCM对GUM不确定度框架通过了验证，且MCM与GUM两者评定出的结果非常接近，达到预期。比较结果有利，GUM不确定度框架适用于此场合及今后足够类似的情形。

6 结束语

MCM的适用范围比GUM法更为广泛，对数学模型没有线性限制，不受输入量相关性以及复杂模型的影响，MCM通过传播测量模型输入量的PDF获得输出量的PDF，从输出量的PDF可以清晰地获得期望、中位数、位置估计、标准偏差等较GUM更为丰富的内容。MATLAB作为一种可视化的高级编程语言，在MCM评定中能快速自动处理几何级倍数的向量、矩阵运算，为MCM在实际中的应用提供了可能[5]。在实际不确定度评定中建议同时采用GUM和MCM两种方法，并对结果进行比较。如若比较结果满意或通过验证，则GUM适用。否则，应采用MCM方法进行评定。

[1]JJF1059.1-2012 测量不确定度评定与表示[S]. 北京：中国质检出版社，2013.

[2]JJF1059.2-2012 用蒙特卡洛法评定测量不确定度[S].北京：中国质检出版社，2013.

[3]JJF1151-2006 车轮动平衡机校准规范[S]. 北京：中国计量出版社，2006.

[4]周桃庚.用蒙特卡洛法评定测量不确定度[M].中国质检出版社：北京，2013.

[5]杨建.蒙特卡罗法评定测量不确定度中相关随机变量的MATLAB实现[J].计测技术，2012,32(4)：51-54.