铝制包装箱搬运过程跌落分析
2014-03-24
(中国核电工程有限公司郑州分公司,河南 郑州 450052)
铝制包装箱搬运过程跌落分析
曲晓宇 花 拓
(中国核电工程有限公司郑州分公司,河南 郑州 450052)
针对某铝制包装箱,对其进行跌落仿真分析,研究其跌落过程中的应力与变形。本文采用ANSYS/LS-DYNA对其进行弹塑性条件下的跌落模拟分析,采用应力失效与应变失效相结合的方法进行安全评定,证明该产品结构满足设计要求。
包装箱;跌落;有限元;仿真分析;LS-DYNA
1 引言
某项目中使用了一种铝制包装箱,经常需要人工搬运,设计要求对该包装箱搬运过程中偶然跌落事件进行动态仿真,分析结构的强度、变形等关键力学性能,保证跌落过程中包装箱不破损。
箱体跌落过程中,在较短时间内,箱体与地面接触碰撞区附近产生高应力区域并发生塑性变形,本文基于弹塑性力学理论,应用有限元软件,得出结构应力应变分布[1-2],应用ANSYS/LS-DYNA程序,采用显式算法求解复杂的接触碰撞问题。
碰撞问题运动方程一般表达式为:

2 有限元仿真设定
2.1 建立模型
计算模型中包装箱主体采用壳单元模拟,箱垫橡胶材料与混凝土地面采用体单元模拟。定义包装箱从离地面h=1.2m处跌落,跌落方式为箱体保持水平沿重力方向向下跌落,并设置重力加速度为9.81m/s2,模型如图1所示。跌落情况下,包装箱在冲击与重力共同作用下形成如下若干次向下跌落——向上弹至最高点——向下跌落的往复运动,但在一个周期作用后,已耗损较多的能量,为缩短计算时长并简化分析,这里仅分析一个周期作用下的运动过程。
2.2 接触算法
结构间的相互作用通过接触计算完成,接触面设置是冲击分析的必要前提,这就需要在可能发生接触作用的结构间定义接触面,接触面能够有效的模拟结构之间的相互作用,并允许连续不断的接触与滑动。接触类型分为三类:即单面接触、点面接触、面面接触。单面接触是LSDYNA程序中应用最为广泛的接触类型,程序将搜索模型中的所有外表面,检查其间是否相互发生穿透。本文采用自动单面接触进行接触分析。
2.3 材料本构
材料的本构是碰撞分析前的重要参数,为了真实的体现材料特性,需建立适合的材料本构关系,由于各种材料本构关系相对复杂,分别做如下定义。
(1)铝材(3003铝材与5A06铝材)选用弹塑性双线性随动材料本构关系,有关参数如表1所示。

表1 铝材材料参数
(2)橡胶材料是各向同性不可压缩的超弹性体,选用Mooney-Rivlin模型构建本构关系,有关参数为常数C10= 0.3375,常数C01= 0.0338,泊松比ν=0.495,密度ρ=870kg/m3。
(3)混凝土地面选用线弹性本构关系,有关参数为弹性模量E= 3×104MPa,泊松比ν= 0.19,密度ρ = 2750 kg/m3。
3 仿真结果分析
3.1 应力分析
包装箱在重力作用下做自由落体运动与地面发生碰撞,伴随碰撞过程,冲击力主要作用于底部与支腿连接处垫板周边区域,此处呈现高应力现象,该区域迅速进入塑性变形阶段并向外扩展。分析等效应力结果,在跌落至最深位置处箱体产生最大应力如图2所示,最大应力点时间历程曲线如图3所示。
3.2 应变分析
撞击过程表明,伴随底部与支腿连接处垫板周边高应力区域的产生并扩大,此处发生最大应变。分析等效应变结果,在跌落至最深位置处箱体产生最大应变,如图4所示。
3.3 结果分析评判

图2 包装箱跌落应力分布
对冲击分析的结果采用应力失效法与应变失效法进行评定。冲击过程中,虽然存在不可恢复的塑性变形,但未造成结构的破坏,认为该结构安全;若等效应力与等效应变超过许可范围,则认为结构破坏或撕裂。即包装箱在受到冲击作用时产生的等效应力应低于材料本身的抗拉强度,产生的等效应变应低于材料延长率。由图2及图4,结构的最大等效应力为52.91MPa,小于材料抗拉强度130 MPa,结构的最大等效应变为0.06,小于材料延长率0.2,包装箱符合安全设计标准。
此外,对包装箱详细分析,在碰撞作用后其产生的结构变形控制在合理范围,不影响内部物料的存贮;结果分析时不考虑橡胶件的破坏失效。
结语
为解决铝制包装箱搬运过程中偶然跌落事故下的跌落冲击问题,应用弹塑性力学理论,采用ANSYS/LS-DYNA分析了该铝制包装箱在水平跌落状态下的力学行为,根据应力失效和应变失效的评定方法进行安全评估,证明此包装箱满足规定的 安全性需求,同时变形也在可控范围内。该冲击计算分析方法对于设计更好的抗跌落、抗冲击产品具有一定的借鉴意义。

图3 包装箱跌落最大应力点时程曲线
[1]张万平,徐定耿,陈松,等.乏燃料贮存格架在组件跌落事故中的冲击分析[J].振动与冲击,2010,29(12):187-189.
[2]张文明,王涛,张华兵,等.基于ANSYS/LS-DYNA船桥碰撞分析[J].中国水运,2006,06(11),21-23.
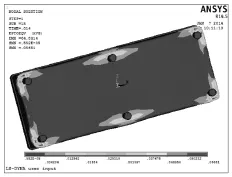
图4 包装箱水平跌落应变分布
[3]柴群,万朝燕.基于ANSYS/LSDYNA的涡轮蜗杆动态接触分析[J].现代制造工程,2006,11,46-48.
[4]郝长千,唐华平,聂拓,等.橡胶缓冲器接触碰撞有限元分析[J].现代制造工程,2009,03,63-65.
TB48 < class="emphasis_bold"> 文献标识码:A
A
