基于小波变换的图像增强算法

陈 莉

(陕西理工学院 物理与电信工程学院， 陕西 汉中 723000)

0 引 言

小波变换具有较好的多分辨率特性，它可以将图像以不同尺度进行分解，利用小波变换将图像变换到频域，不仅可以将图像分解成低频、水平方向高频、垂直方向高频和对角方向高频信息，而且可以将图像进行不同尺度不同分辨率的分解，得到不同尺度的小波分解系数，因此小波变换已在图像处理技术中得到广泛应用[1-3]，现有的利用小波变换进行图像处理的方法是对小波分解后得到的不同尺度的小波系数分别进行处理，由于各层尺度不同，要将处理后的每层小波系数进行逐级重构恢复图像，而每一级的重构都会包含上一层的低频和高频信息，不利于低频信息和高频信息的分离和集中处理。

本文对图像进行多尺度小波分解后没有对各分辨率下不同尺度的小波系数进行处理，而是对分解后的不同尺度不同频率的小波系数进行单支重构，这样就将尺度不同的各层低频和高频信息转换成尺寸大小相同的低频和高频信息，由于尺寸相同，可以根据图像增强的需要，集中提取各层低频或高频重构信息，采用增强技术集中处理，充分分离低频和高频信息，提高图像增强质量。这一思想不仅利用小波变换把图像低频和高频信息进行了分离，又进一步利用单支重构技术实现了对各分辨率下频率信息的集中处理。

1 小波变换及小波分解与重构的快速算法(mallat算法)

1.1 连续小波变换的定义

将任意L2(R)空间中的函数f(t)在小波基下展开，称为f(t)的连续小波变换[4]：

(1)

逆变换：

(2)

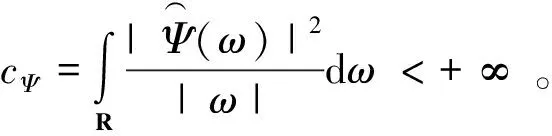
1.2 离散小波的定义

离散小波定义[5]：

(3)

离散小波变换中f(t)和小波信号Ψ*(t)没有被离散，仍然是时间的连续变量，离散的变量是位移值τ和尺度值a。

1.3 信号的分解与重构快速算法(mallat算法)

1.3.1 信号的分解

信号的分解公式[6]：

(4)

(5)

式(4)为低频信号的分解过程，xi+1,k为第i+1级离散低频分解信号，是由上一级(第i级)低频信号xi,k分解而来，从滤波器的设计角度考虑：h为低通滤波器；式(5)为高频细节信息的分解过程，di+1,k为第i+1级离散高频细节分解信号，是由上一级(第i级)高频信号di,k分解而来，从滤波器的设计角度考虑：g为高通滤波器。

1.3.2 信号的重构

信号的重构公式为：

(6)

第i级低频信号xi,n由第(i+1)级低频信号xi+1,k和高频信号di+1,k按式(6)重建得到；h为低通滤波器，g为高通滤波器[6]。

1.4 二维图像的小波多尺度分解与逐级重构

1.4.1 小波多尺度分解

小波多尺度分解的思想是对图像进行不同尺度的分解，既可以大尺度观察图像粗略特征，也可以小尺度观察图像细节特征[6-7]。

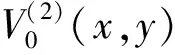
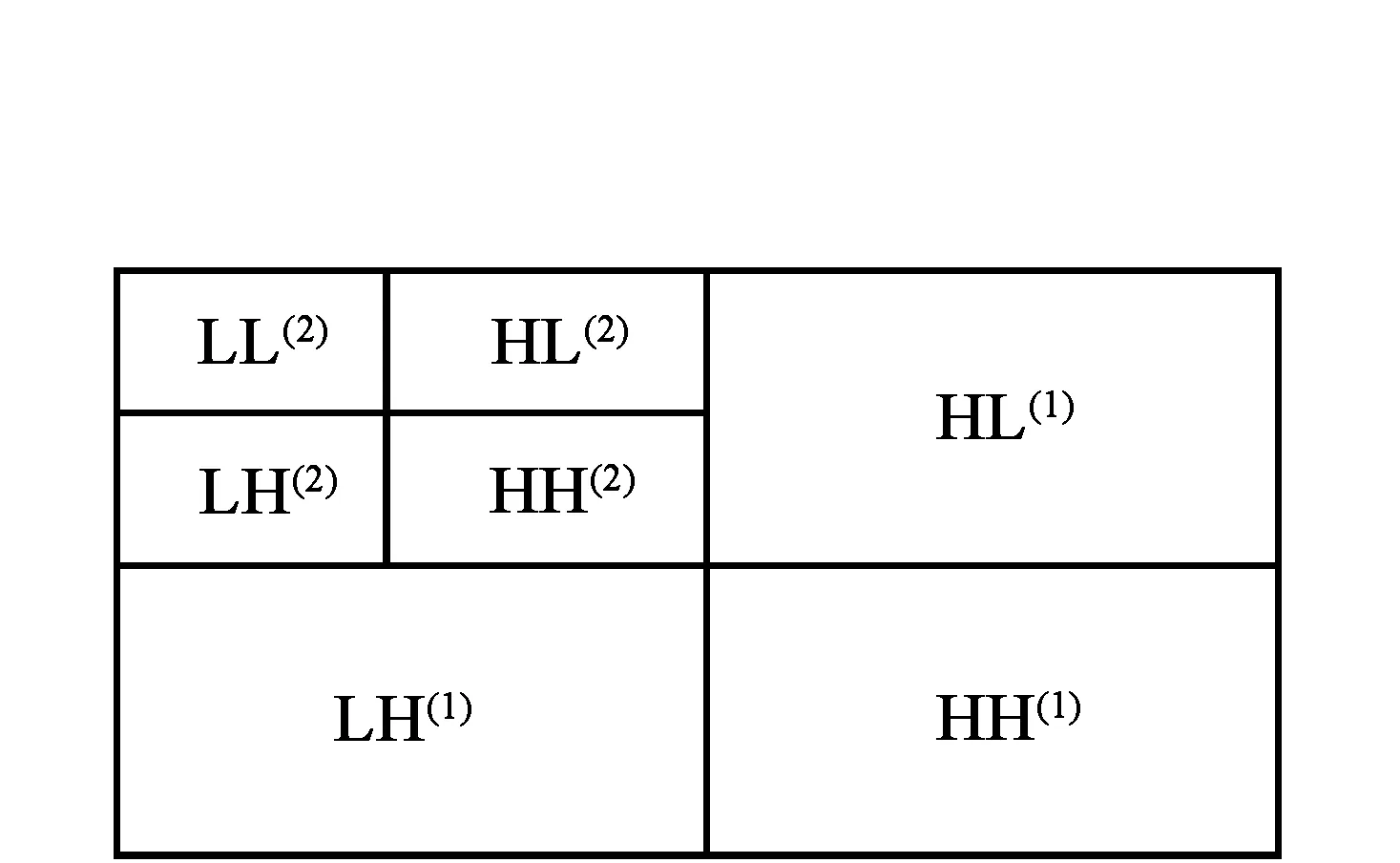
图1 图像小波分解示意图

1.4.2 在MATLAB下对图像进行小波分解

对256×256的lena.bmp图像用syms4小波作2层分解，分解后得到小波系数如图2所示。可以看到原始图像的大小为256×256；做一层分解后低频信息ca1(LL(1))的大小为131×131,它代表图像轮廓信息,集中了图像大部分能量，水平方向高频细节信息ch1(HL(1))的大小为131×131，垂直方向高频细节信息cv1(LH(1))的大小为131×131，对角方向高频细节信息cd1(HH(1))的大小为131×131，这些高频信息描述了图像各方向上的细节信息；二层分解后低频信息ca2(LL(2))的大小为69×69，水平方向高频细节信息ch2(HL(2))的大小为69×69，垂直方向高频细节信息cv2(LH(2))的大小为69×69，对角方向高频细节信息cd2(HH(2))的大小为69×69，各层分解后小波系数大小不同。

(a)原始图像 (b)一层分解 (c)二层分解 图2 MATLAB下图像的2层小波分解图

2 利用小波变换及其单支重构实现的图像增强方法

在多尺度分解的基础上，直接对分解小波系数进行单支重构，得到维数相同的各层重构图。如需要得到图像低频增强信息，只需对各层低频重构信息进行处理并线性叠加，便可得到所需低频信息，且该图像各尺度上的高频信息被滤除；相反，如需要得到高频细节信息，只需对各层高频信息进行处理并线性叠加，便可得到所需高频增强图像，且各尺度低频信息被滤除。

2.1 对分解后各尺度小波系数在MATLAB下的单支重构实现方法

实现步骤：

(1)对256×256 lena.bmp图像利用sym4小波进行2层分解，得到小波分解结构(c,l)，利用wavedec2函数实现。

(2)提取一层分解小波系数：131×131低频系数、131×131水平方向高频系数、131×131垂直方向高频系数、131×131对角方向高频系数；提取二层分解小波系数：69×69低频系数、69×69水平方向高频系数、69×69垂直方向高频系数、69×69对角方向高频系数，利用appcoef2函数提取二层分解低频系数，appcoef1函数提取一层分解低频系数，detcoef2函数提取二层分解各个方向高频小波系数，detcoef1函数提取一层分解各方向高频小波系数。

(3)根据以上小波分解结构和提取的小波系数使用wrcoef2对第二层分解小波系数进行单支重构，利用wrcoef1对第一层分解小波系数进行单支重构，得到的各层重构信息，其尺寸与原始图像尺寸大小相同，均为256×256，在MATLAB下仿真结果如图3所示。

2.2 分段线性增强

分段线性增强的主要思想是对图像实现分段增强处理，这一思想常被用于对原始图像的灰度值进行处理，本文采用这一方法对各层重构信息进行处理，公式如下[9]：

(7)

公式(7)的输入值y(x,y)不是图像灰度值而是图像各层单支重构值，mf表示单支重构信息y(x,y)的最大值，式(7)的算法表示各单支重构信息y(x,y)的取值范围由[a,b]扩展到了[c,d],实现了[a,b]的行拉伸，对[0,a]和[b,mf]的抑制。通过对式(7)中的参数进行调整，改变线段的斜率，可以实现对任意单支重构信息区间进行拉伸或抑制，从而凸显出图像中感兴趣的区域。

2.3 图像增强处理的实现步骤

(a)第一层低频重构 (b)第一层水平高频重构

(c)第一层垂直高频重构 (d)第一层对角高频重构图3 一层小波系数的单支重构图

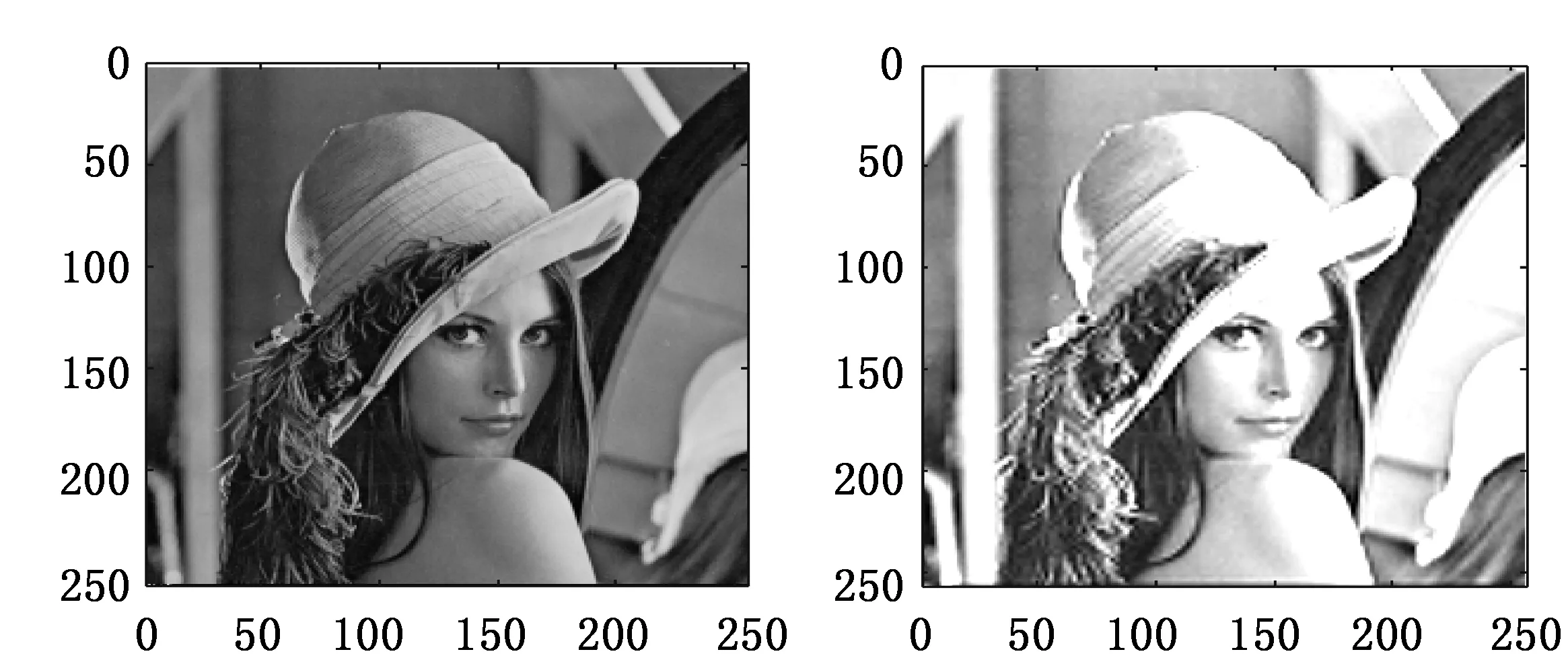
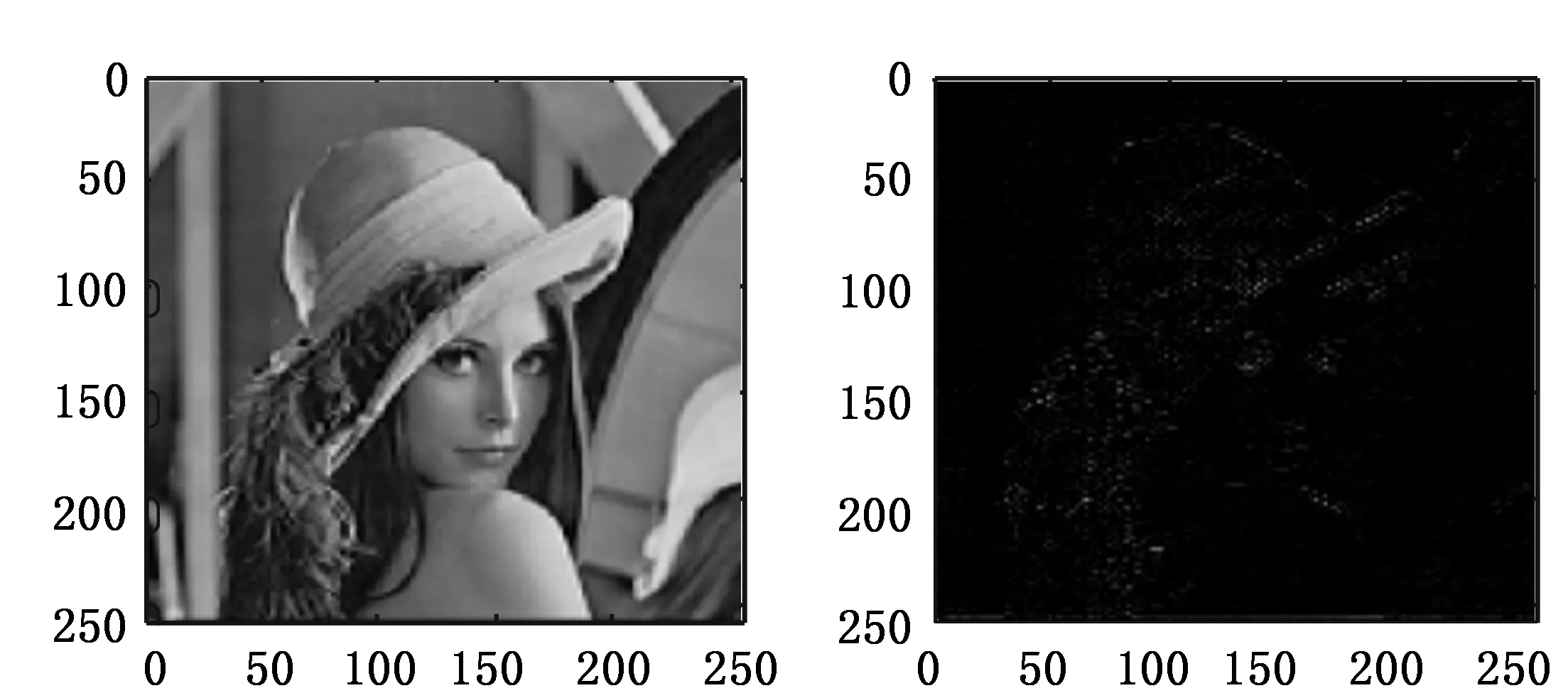
(a)原始图像 (b)一层低频增强图像

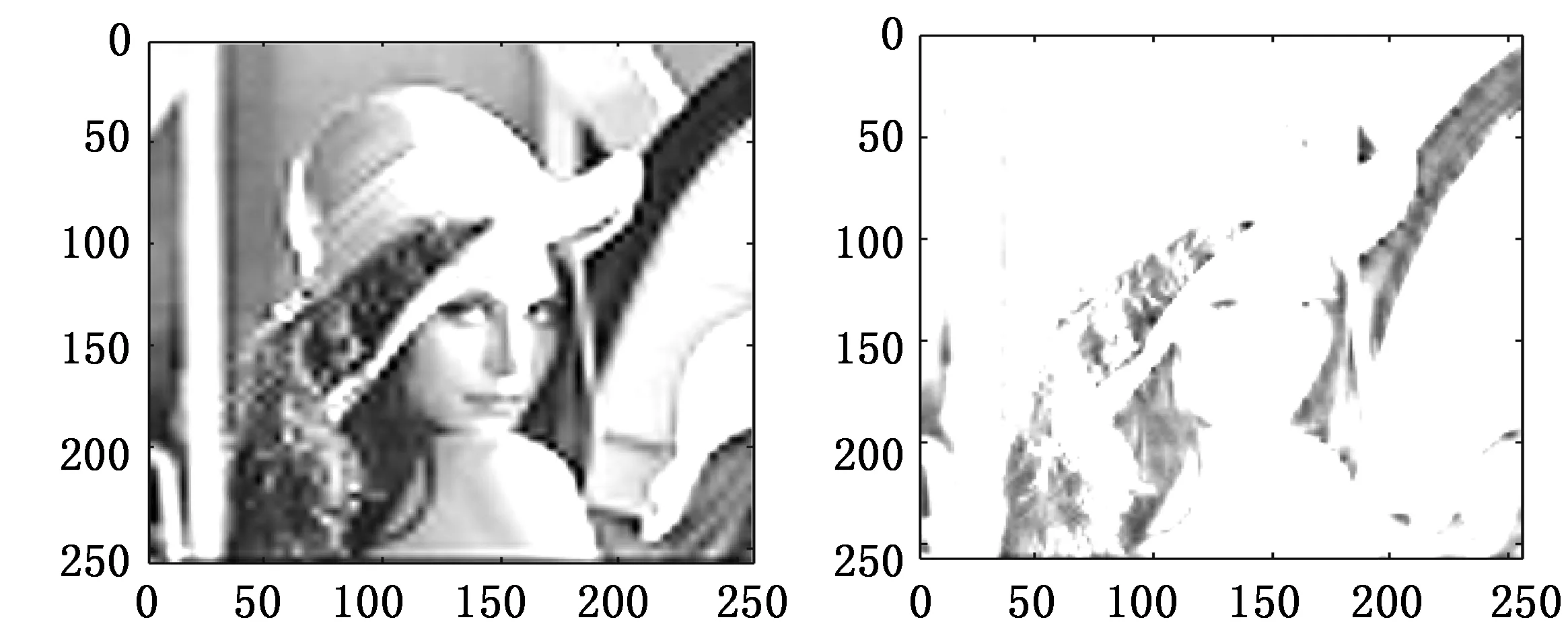
(c)二层低频增强图像 (d)各层增强后低频图像线性叠加图4 低频信息增强图像

(1)在MATLAB下对图像进行多尺度小波分解，得到不同尺度下的低频系数(ca1,ca2,ca3,…)，水平方向高频系数(ch1,ch2,ch3,…)，垂直方向高频系数(cv1,cv2,cv3,…)，对角方向高频系数(cd1,cd2,cd3,…)。

(2)对分解后系数进行单支重构，得到各尺度下单支重构值：低频各尺度单支重构(a1,a2,a3,…)；水平方向各尺度单支重构(h1,h2,h3,…)；垂直方向各尺度单支重构(v1,v2,v3,…)；对角方向各尺度单支重构(d1,d2,d3,…)。

(3)对低频重构值进行分段线性增强并对增强后值进行加权平均。对处理后的各层重构值进行线性叠加可得到处理后图像，该图像的低频信息得到了增强，充分分离高频信息。

(4)对各层各方向高频信息进行分段线性增强后加权平均，将处理后各层各频率重构值进行线性叠加，可得到高频信息增强图像，该图像只保留细节信息。充分分离低频信息，细节信息将得到增强。

(5)对各层低频重构值进行分段线性增强并对增强后值进行加权平均，对各层各方向高频信息进行分段线性增强后加权平均，对处理后的各层重构值进行线性叠加可得低频和高频信息均得到增强的图像。

3 实验结果及分析

对256×256 lena.bmp图像用sym4小波做2层分解，对各层小波分解系数做单支重构得到各层不同频率重构信息，实验中首先提取各层低频重构信息，对其做线性分段增强，得到如图4所示一层低频增强图像，二层低频增强图像，再将增强后各层低频重构信息线性叠加得到如图4(d)所示各层低频集中处理增强图像，从图4中可以看出集中处理后的低频增强图像其增强效果优于一层和二层低频增强图像。

提取各层高频细节对其分别做分段线性增强，得到如图5所示一层和二层各方向高频细节增强图像，对其线性叠加，得到如图5(g)所示的各层高频边缘细节集中处理增强图像，可以看出经过增强处理后图像高频细节信息得到明显增强。

(a)一层水平高频增强图像 (b)一层垂直高频增强图像 (c)一层对角高频增强图像

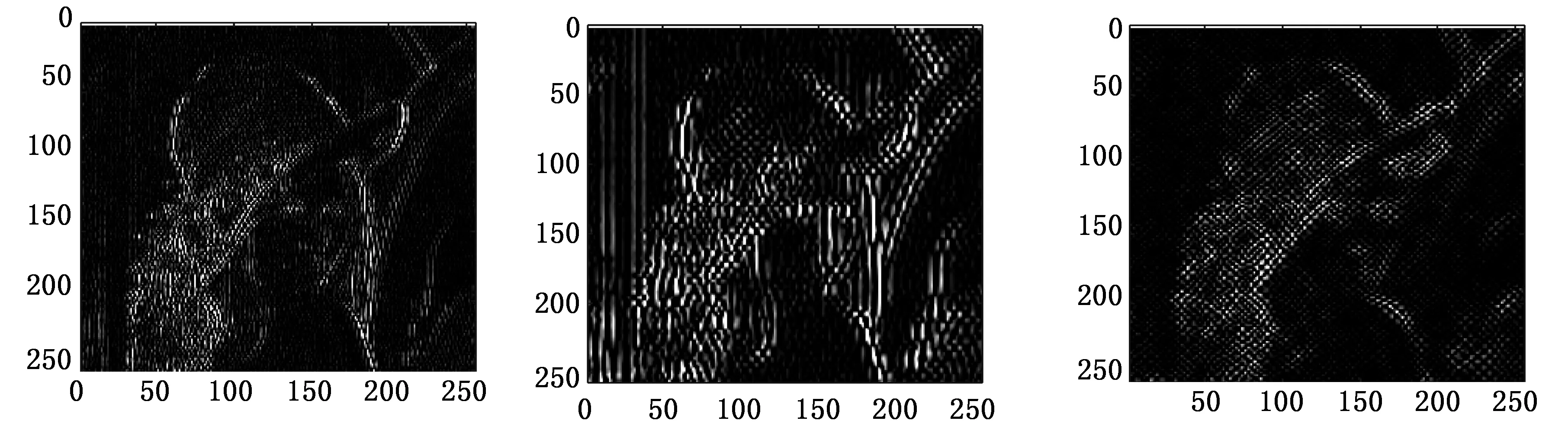
(d)二层水平高频增强图像 (e)二层垂直高频增强图像 (f)二层对角高频增强图像

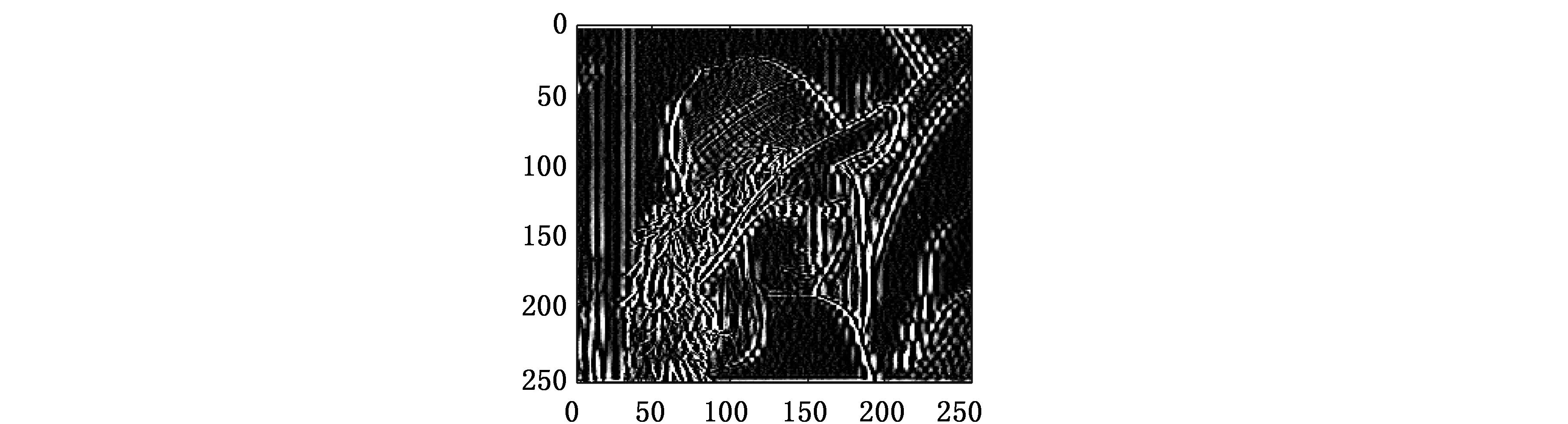
(g)各层增强后高频图像线性叠加

对各层低频和高频信息同时做如上所述增强处理可得到如图6所示低频高频同时增强图像，与原始图像对比增强后图像的轮廓和细节信息得到增强，且效果明显。

(a)原始图像 (b)低频高频同时增强图像图6 低频、高频信息同时增强图像

4 结束语

算法在处理的过程中将高频信息和低频信息充分分离出来，有效提高了不同频率成分图像的增强效果；把在空域采用的分段线性增强技术应用到对小波单支重构值的处理上，达到了对各尺度高频或低频信息增强的目的，实验结果表明：算法具有很高的灵活度，既可以对图像低频信息增强，又可以对图像高频边缘细节信息增强。

[参考文献]

[1] 刘兴淼,王仕成,赵静.基于小波变换与模糊理论的图像增强算法研究[J].弹箭与制导学报,2010,30(4):183-186.

[2] 王剑平,张婕.小波变换在数字图像处理中的应用[J].现代电子技术,2011,34(1)：91-94.

[3] 刘洲峰,徐庆伟，李春雷.基于小波变换的图像分割研究[J].计算机应用与软件,2009,26(4):62-66.

[4] 李建平.小波分析与信号处理[M].重庆:重庆出版社,1997:100-300．

[5] MALLAT S.信号处理的小波导引[M].2版.杨力华,戴道清,黄文良,等,译.北京:机械工业出版社，2002.

[6] MALLAT S G.A theory for multiresolution signal decomposition:the wavelet respentation[J].IEEE Transactions On Pattern Analysis and Machine Intelligence,1989,11(7):674-693.

[7] 秦前清.实用小波分析[M].西安:西安电子科技出版社,1998.

[8] 冉启文.小波变换与分数傅立叶变换理论及应用[M].哈尔滨:哈尔滨工业大学出版社,2001.

[9] 李朝辉,张弘.数字图像处理及应用[M].北京:机械工业出版社,2004.

[10] 李海云,于红玉.基于小波多尺度分辨的多模医学图像融合算法研究[J].中国医疗器械杂志,2004(2):115-116.

[11] 张彬,郑永果,马芳,等.基于小波变换的多模态医学图像融合算法[J].重庆医学,2011(7):652-654.

[12] 武杰,聂生东,汪红志,等.基于局部特征的医学图像融合方法[J].中国医学影像技术,2009(3):496-498.