GPS地表监测数据去噪技术

李卫东

(河北金山矿业有限公司总经理, 河北 邢台市 054100)

0 引 言

西郝庄矿矿区进行了多年开采，目前地表存有以前露天开采遗留的露天坑及堆存岩土，地面已出现多处塌陷及较大范围的裂缝。为此，设立西郝庄铁矿采空区GPS地表沉降监测系统，应用现代化的传感和网络通讯技术对地表沉降进行实时监测，及时掌握地表沉降信息，为地压灾害预测提供依据。

由于各种干扰因素的作用，GPS监测数据中的有用信号和噪声的时域和频域特性通常是不一样的，有用信号在时域和频域上具有局部化特征，表现为低频特性或是一些比较平稳的信号；而噪声在时域与频域空间中的分布具有全局性特征，它在整个数据监测与数据采集的时域内处处存在，在频域上表现为高频特性。根据此特性，对其可以通过限定阀值形式对小波系数进行处理，从而降低噪声部分值，再通过信号重构恢复信号，实现有用信号和噪声的分离，实现降噪的目标。

由于Daubechies小波具有很好的正交性、紧支性(紧支撑长度为2N-1)、正则性、近似对称性和适用Mallat快速算法等特点，其时域分析优良，在监测信号的奇异性中具有很大优势，适用于地表监测数据的处理，且在许多工程领域中应用比较成熟。dbN中N越大，其滤波的长度越长，其中db4具有最短的时窗和最高的时间分辨率，去噪效果良好。下面着重介绍Daubechies去噪小波的基本原理。

1 去噪小波的构 造方法

1.1 基本原理

构造去噪小波的充要条件是：对于离散滤波器h={h1，h2，…，hN}，两尺度方程

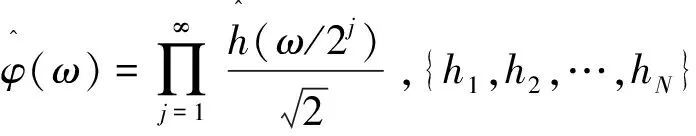
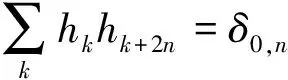
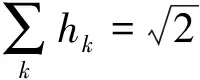
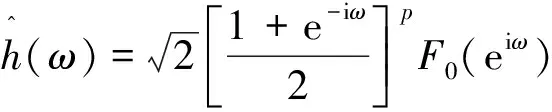
其中，当ω=π，F0(eiω)≠0，且|F0(eiω)|在ω=0～2π范围内的上界≤2p-1。

若{h1，h2，…，hN}满足上述条件(1)～(3)，则φ(t)只存在一个解，并且φ(t)是紧支撑正交尺度函数，其支撑区间[0，N]。若令gn=(-1)nh1-n，则

1.2 Daubechies紧支撑正交小波的构造方法

若ψ(t)有p阶消失矩，则对于任何p-1次多项式x(t)=a0+a1t+…+ap-1tp-1，都有〈ψ(t),x(t)〉=0，即ψ(t)与任何p-1次多项式都是正交的。由于

将f(t+2-jk)在2-jk处展开，得

由于ψ(t)有p阶消失矩，则

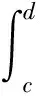
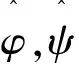
(1) 小波函数ψ(t)具有p阶消失矩；

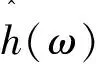
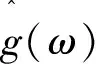
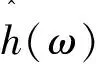
其中，当ω=π，F0(eiω)≠0。

取上式的z变换，z=eiω，即

当ω=π，z=-1，F0(-1)≠0。

构造Daobechies紧支撑正交小波滤波器的关键是：合理选择F0(eiω)或F0(z)，可选方案为：

Daobechies小波的支撑[-p+1，p+1]，尺度函数的支撑[0，2p-1]。

1.3 紧支撑正交小波的构造方法的实现形式

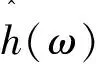
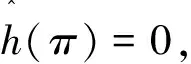
h0+(-1)h1e-iω+(-1)2h2+…+(-1)NhN=0

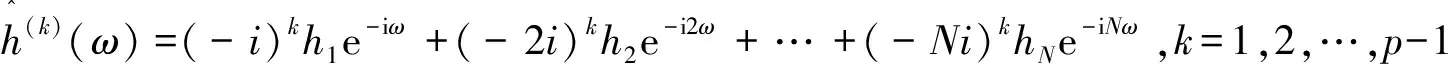
(-1)(-i)kh1+(-1)2(-2i)kh2+…+(-1)N(-Ni)khN=0

h1-2kh2+…+(-1)N-1NkhN=0，k=1，2，…，p-1

总结起来，可得

2 监测数据去噪实现技术

2.1 去噪实现过程

(1) 选择小波函数和小波分解层数，计算监测数据到第N层的小波分解。小波分解层数的选择也同样影响着数据去噪的效果，若分解层次较少,则可能去噪不彻底，若分解层数太多，则影响计算速度，同时使得部分有用信号消除，且当分解到一定程度后，滤波后的信号几乎保持不变。

(2) 高频系数的阀值选择。阀值选取分为以下6种形式。

第1种是硬阀值形式，即把含噪的小波系数的绝对值与所选定的阀值λ进行比较，将小于等于阀值λ的点变为0，大于阀值λ的点保持不变。

硬阀值法具有彻底去噪的特点，同时也使得信号失去了有用成分。

第2种是软阀值形式，即把含噪的小波系数与所选定的阀值λ进行比较，将大于阀值的点收缩为该点值与阀值的差；将小于阀值相反数的点扩展为该点值与阀值的和；将绝对值小于等于阀值的点变为0。

在处理GPS监测数据时，从第一层到第J层，每一层选择一个软阀值。阀值λ的计算公式为：

这样具有更好的去噪效果。λ对于不同的信号具有自适应性，去噪彻底，同时也不会去除有用信号，N是数据个数；J是分解层数；σ为监测数据的标准方差，计算方法如下：

式中，median为去中值函数，{wJ-1，k，k=1，2，…，2J-1}为小波细节系数。

第3种是强制去噪法，即强制所有分解层下的细节系数置全为0。

{wj-1，k，j=1，2，…，J；k=1，2，…，2j-1}

第4种是Garrote去噪法，即把含噪的小波系数的绝对值与所选定的阀值λ进行比较，将小于等于阀值λ的点变为0，而对大于阀值λ的点按如下公式计算：

第5种是Birge-Massart阈值去噪法，给定一个指定的分解层数j，对j+1以及更高层所有系数保留；对i层(1≤i≤j)，保留绝对值最大的ni个系数并确定：

式中，α为经验系数，在信号降噪情况下取α=3；缺省情况下取S=L(1)，即第1层分解后系数的长度，一般情况下，S满足L(1)≤S≤2L(1)。设对信号进行i层分解，每层保留的小波系数个数最多为n，由于每层保留的小波系数个数不同，系数较少的层数采取补零的方法使每层系数个数相同，从而形成小波变换值矩阵。

第6种是Semisoft阐值函数，即把含噪的小波系数的绝对值与所选定的阀值λ1和λ2进行比较，按如下公式计算小波系数：

2.2 去噪效果分析

假设所收集到的GPS监测数据为序列为:

s1，s2，…，sN

该序列含有噪声。通过采用小波方法进行去噪，得到去噪后的GPS监测数据序列为

v1，v2，…，vN

则残差为

ri=si-vii=1，2，…，N

2.2.1 残差统计指标

(1) 最大值:max=max{r1，r2，…，rN}。

(2) 最小值：min=min{r1，r2，…，rN}。

(3) 极差：range=max-min。

(6) 频度：mf={r1，r2，…，rN}中出现次数最多的那个值。

(11) 偏态系数：

(12)峰态系数：

(13) 变异系数：

(14)自相关系数：

有偏自相关系数：

无偏自相关系数：

计算上述自相关系数的函数是autocorr(r)，若用xcov(r)计算，则所得结果是对称的，即ACF-j=ACFjACF-N+1,ACF-N+2,…,ACF-1,ACF0,ACF1,…,ACFN-1

2.2.2 残差直方图。

将残差序列{r1，r2，…，rN}分成若干个长度相等的区间，统计每个区间内残差值出现的次数，生成残差直方图。从残差直方图能看出残差的分布。

2.2.3 残差FFT分析

对残差序列r={r1，r2，…，rN}进行FFT分析的方法是：

F=fft(r，N)

当k=0，1，…，N-1时，

频率：f=k/(NΔt)，Δt为取样时间间隔；

幅值：A=2|F|/N=2abs(F)/N；

相位：α=angle(F)。

3 各监测点监测数据净变化量去噪

GPS01监测数据去噪过程如图1～3所示。

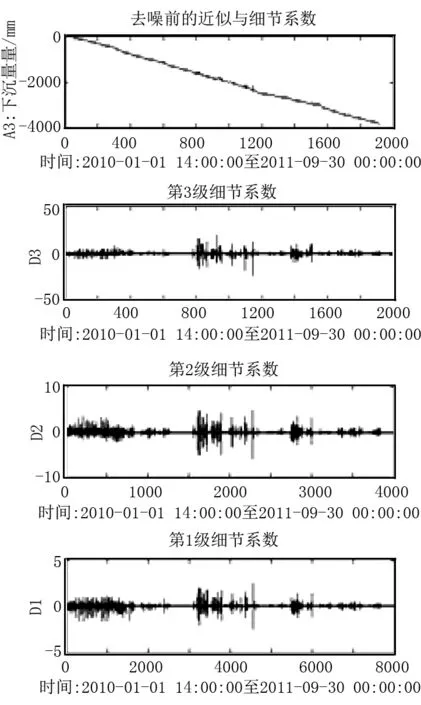
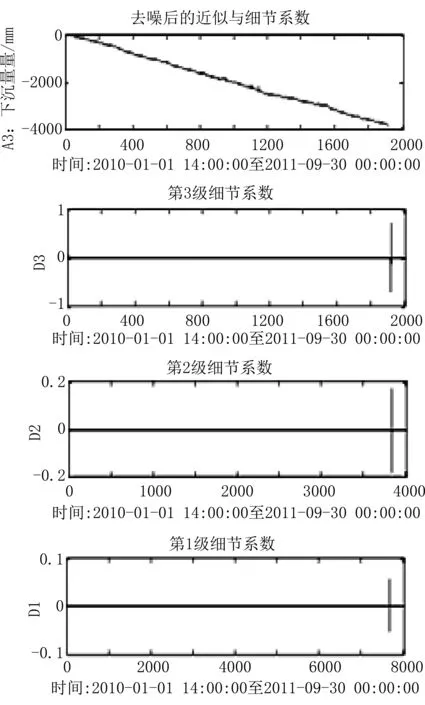
图1 GPS01点z方向监测数据的分解

其他方向的去噪方法一样，在此不再赘述。

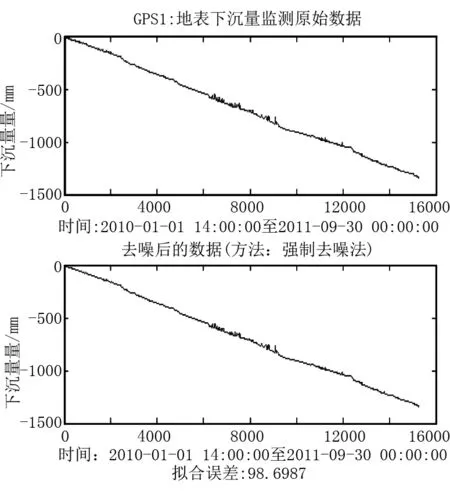
图2 GP01点z方向监测数据的去噪

4 结 论

本文介绍了GPS监测数据去噪几种常用技术的原理及其实现过程。欲达到良好的去噪效果，选择合适的技术参数是关键。

图3 GP01点z方向监测数据的残值分析