基于参数优化的扩容电力系统结构稳定的自愈控制*

李小华，刘 洋，姜本源，徐艳影

(1.辽宁科技大学电子与信息工程学院，辽宁 鞍山 114051;2.辽宁科技大学理学院，辽宁 鞍山 114051)

进入21世纪以来，人类对电力的依赖程度加大，智能电网应运而生，在近期已成为全球电力行业研究和探讨的热点[1]。在智能电网中有一个突出的特征是具有灵活的拓扑结构，也即是说当系统出现故障导致网络拓扑结构重构时，系统应能够通过自身的调节作用快速的自我恢复，而使系统保持自身的稳定运行状态，避免停电事故的发生。这就是智能电网中所说的“自愈”功能的一部分[2]，它也是电网智能化的一个标志。但是目前智能电网概念中对此功能的研究仅限于系统故障后的拓扑结构重构，而对于有新结构并网时即扩容时的拓扑结构重构则没有涉及。应该知道，这两种结构重构研究起来是有本质不同的，前者是在原结构基础上的结构变化，后者实际上是结构的扩展。目前尚没有发现有文献对此问题进行研究。

结构的自愈控制问题从控制角度看应该属于大系统结构关联稳定性的问题。而关联稳定这方面的研究已有很多，如文献[3-6]。但在现有的文献中，大部分只考虑了固定结构系统的鲁棒分散控制问题，却鲜有结构扩展时的关联稳定性的研究文章。文献[7]是最早提出扩展结构系统的分散控制问题的，它采用频域法来解决该问题，算法比较繁琐；文献[8]首先定义了扩展结构系统有机结构控制的概念，研究了此类系统基于状态反馈的鲁棒分散关联镇定方法；文献[9]则研究了其基于动态输出反馈的鲁棒分散关联镇定方法。它们均采用了线性矩阵不等式(LMI)方法，但是，一般在求解最后获得的LMI中，有的参数则需要事先人为选择，如文中互联约束矩阵的选择。这个矩阵选择的好坏则决定了该控制设计的性能，当选择不当时，还可能会使系统暂态性能很差，甚至不稳定，一些文献中一般只提供了一种单位阵的选择方法，按照这种方法选择，性能往往不能尽如人意。因此，为了避免设计参数选择的盲目性，得到更好的控制效果，本文针对扩容电力系统自动发电控制设计，结合动态输出反馈和遗传算法提出一种优化的扩展结构大系统鲁棒分散关联控制方法，该方法可以保证电力系统在线扩容时对拓扑结构重构的适应性，维持系统的稳定运行，因此可看做是扩容时系统的自愈控制。该控制设计是在不改变原有结构系统控制律的条件下，利用LMI方法推导出新加入子系统动态输出反馈控制律求法，再用遗传算法对问题求解中的互联约束矩阵参数进行优化，以达到改善系统控制性能的目的。

1 扩容电力系统的数学描述

1.1 互联电力系统模型

考虑一类多区域互联电力系统，它的每个区域包括两个发电机组，即一个水电机组和一个火电机组。根据参考文献[8]，结合自动发电控制AGC的偏差控制，第i个区域的子系统模型为：

yi=Cixi+ηi

(1)

其中xi∈Rni，ui∈Rmi，ξi∈Rni，yi∈Rli，ηi∈Rli分别为子系统的状态、输入、不确定扰动输入和输出的测量噪声向量。在第i个区域子系统中选择各变量与稳态值的偏差量，即气轮机阀门开度变化量ΔaT，气轮机高、中、低压输出变化量Δpt1,Δpt2和Δpt3，水轮机阀门开度变化量ΔaH，水轮机缓冲器活塞位置变化量ΔvH，水轮机的水流量Δq以及频率变化量Δf为其状态变量，选择气轮机输出变化量ΔpT，水电机组输出变化量ΔpH以及区域频率变化量Δf为其输出变量，即：

xi=[ΔaTi,Δpt1i,Δpt2i,Δpt3i,ΔaHi,ΔvHi,Δqi,Δfi]T

yi=[ΔpTi,ΔpHi,Δfi,Δvi,Δpei]T

1.2 基于输出反馈的扩容电力系统数学描述

(2)

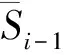
设原系统具有分散动态输出反馈控制器，为

(3)

(4)

将式(4)写成闭环形式

(5)

研究在原电力系统结构的基础上扩展新结构。设Si为电力系统新加入的区域子系统，其方程描述为

Si：Xi=AiiXi+Biui+Givi

yi=CiXi

wi=HiXi

(6)

其中，Xi为第i个子系统的状态，ui为第i个子系统的控制输入，yi为第i个子系统的输出，vi为子系统间互联的输入，wi为子系统间互联的输出。Ai、Bi、Ci、Gi及Hi是具有一定维数的常数矩阵。设计子系统Si的动态输出反馈控制器为

ui=CkiXki+Dkiyi

(7)

其中，Xki∈Rn是控制器本身的状态，Aki，Bki，Cki，Dki是具有相应维数的常数矩阵。同理将输出反馈控制器(7)代入系统(6)中，即可得到一个如下形式的系统

(8)

将式(8)写成闭环形式：

(9)

(10)

利用式(10)的关系将式(5)和(9)两部分系统进行合并，闭环后，系统模型可表示为

(11)

对于系统(11)可以认为该系统的互联部分是时变的、不确定的，但其变化是有界的。为了研究方便将扩容系统简化重写为

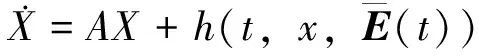
(12)

其中

设系统的互联项满足二次约束

(13)

2 扩容电力系统结构关联稳定的自愈控制设计

2.1 动态输出反馈控制器设计

根据模型(12)来研究动态输出反馈条件下扩展结构电力系统的结构自愈控制问题。由于扩展结构系统一般是在原结构系统运行期间加入新的子系统，因此不能改变原有结构系统的分散控制律，这就要求在此基础上，设计新加入子系统的分散控制律，使其能够在稳定自身的同时稳定整个被扩展后的大系统，并使大系统关联稳定。所以，这里假设原结构系统的控制设计已存在了，来研究的扩展结构子系统的分散控制律。它实际上就是研究新加入子系统基于动态输出反馈的鲁棒关联分散控制问题，即保证系统拓扑结构稳定的自愈控制。

定理1 对于扩展结构电力系统(12)，若存在对称正定矩阵Pi以及矩阵Mi和Ni，通过选择合适的互联约束矩阵Qi，使得 (14)式成立

P>0

(14)

其中：

则扩展结构电力系统(12)是鲁棒分散关联稳定的。

证明引入二次Lyapunov函数：

V(X)=XTPX

且设P>0，P为对称正定矩阵:

闭环系统鲁棒稳定的充分条件是

将上式写成矩阵不等式可等效为

P>0

(15)

而(13)式也写成矩阵不等式形式

(16)

运用S-过程[11]，作式(15)-τ(16)，其中τ>0，可以得到

P>0

(17)

利用Schur补引理[11]，有

(18)

这里：

因为在互联约束中考虑了互联项的参数不确定性和结构参数不确定性，因而扩展结构系统是鲁棒的，且结构关联稳定的。证毕

定理2 如果(14)式是可解的，那么原来的非凸的动态输出反馈问题也是可解的。则新加入子系统的输出反馈鲁棒分散控制律即结构自愈控制律为

证明由上面定理的证明即可得出。

2.2 控制设计的优化

由于在(17)式的求解中涉及到互联约束矩阵Qi和Qi-1的选择问题，研究发现这两个参数与系统的性能有很大的关系，选择不好会影响控制设计效果，因此考虑用遗传算法对此进行优化。由于大系统的维数比较高，本文将互联约束矩阵取为上三角矩阵进行优化，以减少待优化参数。

遗传算法是一种成熟的且具有广泛适用性的全局优化方法，在搜索进化过程中可用适应度函数来评价个体的优劣，因而适应度函数的选择是整个优化过程的关键。本文以系统时域阶跃响应性能参数作为控制器参数的鲁棒性评价指标，选用适应度函数如下：

J=w1σ+w2ts

(18)

其中，σ是超调量，ts是调整时间，为了不同参数能够统一评价，σ按设定值进行归一化，ts按300 s进行了归一化。由式(18)可见，该适应度函数综合了系统时域阶跃响应的超调量、上升时间，同时考虑到不同的控制场合的性能要求，该适应度函数的各个性能指标可以通过不同的加权系数来调节。应用遗传算法时，可对互联矩阵中的上三角元素进行二进制编码，选择适当的遗传算子优化计算参数。适应度函数的计算需要求解上述问题(14)，并将解代入系统中，仿真出各性能指标。可采用Matlab工具箱编程实现该优化过程。

3 仿真研究

考虑一个扩展结构互联电力系统，设原结构为一个区域，已设计好系统的控制器，然后在此区域基础上在线扩容再加入另一个区域系统，这两个区域互联电力系统的模型如(1)式所示，其中数据可参考文献[8]。按照上述方法设计扩展系统的控制器，利用MATLAB仿真了系统在阶跃负载扰动下的系统频率偏差量及区域间交换功率偏差量的变化曲线。此次仿真中适应度函数的加权为w1=0.5，w2=0.5。仿真结果如图1。

图1 遗传算法优化前后的扩容电力系统主要输出响应曲线

图中实线为优化前的输出响应曲线，虚线为遗传算法优化后的输出响应曲线，通过仿真曲线看出，本文的设计方法可以使扩容后即拓扑结构变化后的各个子系统稳定运行，优化前后的系统中每个子系统的频率变化量和交换功率变化量均达到了零，即均达到了电力系统负荷频率控制的要求，且遗传算法优化后系统的超调量明显减小，频率增量曲线的震荡次数也明显减少，控制性能得到明显改善。

为了检验其关联稳定性，将该系统的某个关联断开后，再对其进行仿真。系统响应如图2所示。其中实线为优化前曲线，虚线为优化后曲线。系统经过一段时间的波动后，输出响应曲线最终稳定到0。对于互联电力系统中的偏差控制系统而言，这就表示系统最终能够保持稳定，具有稳定性。仿真结果充分说明了该系统是分散关联稳定的，优化后

图2 断开一个关联后扩容电力系统的主要输出响应曲线

系统具有更好的控制性能。进而也说明该设计方法具有结构自愈控制的效果，说明了方法的正确性、有效性和实用性。

在互联电力系统的仿真研究中发现适应度函数权重的选择不同，优化后的性能指标会有很大变化。若加大超调量的权值，取w1=0.75，w2=0.25时的系统仿真研究结果如图3所示。

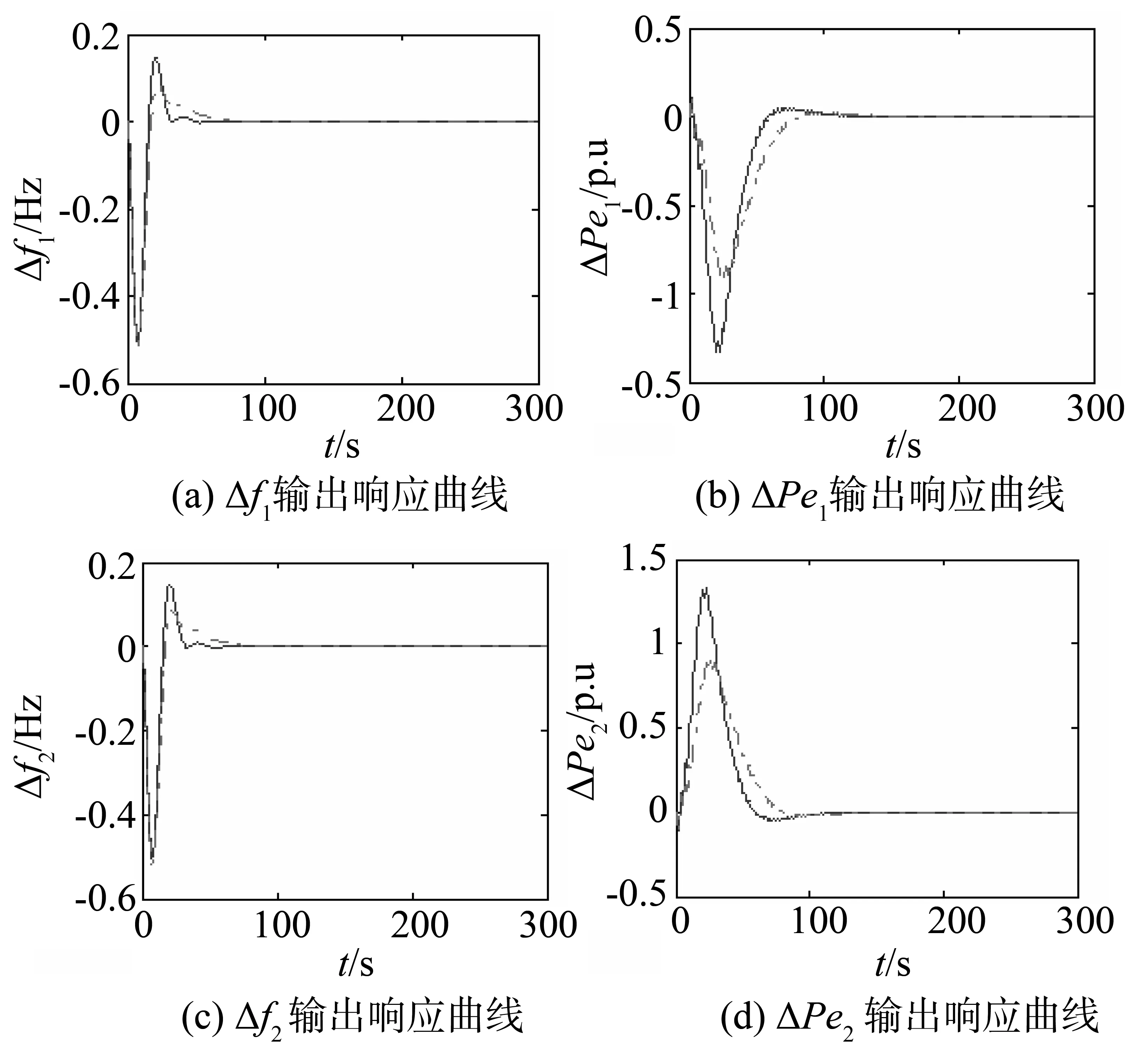
图3 w1=0.75, w2=0.25时扩容电力系统输出响应曲线对比图

图中虚线为加大超调量权值后的曲线。由仿真曲线可以看出加大超调量的权值后系统的超调量减小，而调节时间的变化不是很大，因此经过实验当w1=0.75，w2=0.25时的控制效果是最好的，系统的性能达到最佳。此时通过仿真求得的系统自主分散反馈控制律为：

4 结 论

本文结合电力系统的自动发电控制设计，研究了电力系统在线扩容即拓扑结构扩展时能保持系统稳定的结构自愈控制问题。主要基于动态输出反馈、LMI方法和参数优化算法，设计了扩容电力系统新加入子系统的鲁棒关联稳定控制器，该控制律是在不改变原结构电力系统的分散控制律的基础上设计的，它不仅可以镇定新加入的子系统，而且可以保证整个扩容后系统都是关联稳定的。由于利用遗传算法对互联约束矩阵参数进行了优化，所以系统的控制性能得到了明显改进。文中结合电力系统的实例对所提出方法进行了仿真研究，从结果可以看出该方法是有效的，且优化后具有更好的控制性能。

参考文献：

[1]何光宇，孙英云，梅生伟.等.多指标自趋优的智能电网[J].电力系统自动化，2009，33(17)：1-5.

[2]陈树勇, 宋书芳, 李兰欣, 等. 智能电网技术综述[J]. 电网技术,2009, 33(8): 1-7.

[3]SILJAK D D. Large-scale dynamic systems: stability and structure[M].New York:North-Holland,1978.

[4]SILJAK D D. Organically-structured control[C]. Proceedings of the American Control Conference, 2001:2736-2742.

[5]FRANCESCO A, NICOLA G. A formal framework for connective stability of highly decentralized cooperative negotiations[J]. Autonomous Agents and Multi-Agent Systems,2007, 15(3): 253-279.

[6]欧阳鑫玉，陈雪波.一类动态互联复杂系统的稳定性分析[J].控制与决策，2009, 24(11): 1749-1752.

[7]TAN X L, IKEDA M. Decentralized stabilization for expanding construction of large- scale systems[J]. IEEE Transactions on automatic control, 1990, 15: 644-651.

[8]李小华. 复杂大系统的有机结构控制及其应用研究[D]. 沈阳：东北大学，2006.

[9]LI X H, LI H Y. Robust decentralized connective stabilization of large-scale systems with expanding construction based on dynamic output feedback[C]∥ Proc of the 23thChinese Control and Decision Conference, Mianyang, Sichuan, 2011:774-778.

[10]陈雪波. 系统包含原理及其应用[M]. 北京：科学出版社, 2012.

[11]郭洪艳. 基于LMI的多区域互联电力系统鲁棒分散控制设计[D]. 鞍山：辽宁科技大学, 2007.

[12]俞立. 鲁棒控制-线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002.

[13]钱伟, 沈国江. 基于LMI的线性时滞系统输出动态反馈镇定[J]. 控制与决策, 2008, 23(5): 546-550.