基于按指数律拓展的分数阶积分的El-Nabulsi-Pfaff变分问题的Noether对称性*

丁金凤 , 张 毅

(1. 苏州科技学院 数理学院，江苏 苏州215009；2. 苏州科技学院 土木工程学院，江苏 苏州215009)

1 El-Nabulsi-Pfaff变分问题

基于按指数律拓展的分数阶积分的El-Nabulsi-Pfaff变分问题定义为[19]：

求积分泛函

(cosht-coshτ)α-1dτ

(1)

在给定边界条件

(2)

如果aμ=aμ(τ)是El-Nabulsi-Pfaff变分问题的极值，则满足如下的El-Nabulsi-Birkhoff方程[19]

(μ=1,…,2n)

(3)

泛函(1)称为El-Nabulsi-Pfaff作用量。当α=1时，这个问题成为经典的Pfaff变分问题，而方程(3)成为标准的Birkhoff方程。

2 El-Nabulsi-Pfaff作用量的变分

引入r-参数有限变换群的无限小变换

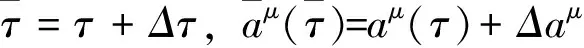
(μ=1,…,2n)

(4)

其展开式

(5)

(6)

El-Nabulsi-Pfaff作用量(1)在变换前后的差为

(cosht-coshτ)α-1dτ=

B(τ+Δτ,aν+Δaν)] ·

(7)

(8)

由于

(9)

利用式(9)，式(8)可写成

(10)

将式(5)代入式(10)，得到

(11)

式(8)和(11)是基于按指数律拓展的分数阶积分的El-Nabulsi-Pfaff作用量变分的基本公式。

3 Noether对称性的定义和判据

定义1 如果El-Nabulsi-Pfaff作用量(1)是无限小群变换(4)的不变量，即对无限小群变换(4)的每一个变换，始终成立如下关系

ΔS=0

(12)

则称无限小变换为Birkhoff系统基于按指数律拓展的分数阶积分的变分问题的Noether对称变换。

根据定义1和公式(8)，(11)，得到如下判据。

判据1 如果无限小群变换(4)满足如下关系

(13)

那么，变换是Birkhoff系统在定义1意义下的Noether对称变换。

式(13)可写成r个方程

(σ=1,…,r)

(14)

当r=1时，方程(14)称为Birkhoff系统基于按指数律拓展的分数阶积分的变分问题的Noether等式。

通过判据1或Noether等式(14)可以判断Birkhoff系统基于按指数律拓展的分数阶积分的变分问题的Noether对称性。

定义2 如果El-Nabulsi-Pfaff作用量(1)是无限小群变换(4)的准不变量，即对无限小群变换(4)的每一个变换，始终成立如下关系

(15)

其中ΔG=εσGσ，Gσ=Gσ(τ,aν)称为规范函数，则称无限小变换为Birkhoff系统基于按指数律拓展的分数阶积分的变分问题的Noether准对称变换。

根据定义2和公式(8)，(11)，得到如下判据。

判据2 如果无限小群变换(4)满足如下关系

(16)

那么，变换是Birkhoff系统在定义2意义下的Noether准对称变换。

式(16)可写成r个方程

(17)

当r=1时，方程(17)称为Birkhoff系统基于按指数律拓展的分数阶积分的变分问题的Noether等式。

通过判据2或Noether等式(17)可以判断Birkhoff系统基于按指数律拓展的分数阶积分的变分问题的Noether准对称性。

4 Noether定理

在El-Nabulsi动力学模型下，由Birkhoff系统的Noether对称性可直接导出Noether守恒量，有如下定理。

定理1 对于El-Nabulsi动力学模型下的Birkhoff系统(3)，如果无限小群变换(4)是定义1意义下的Noether对称变换，则系统存在r个线性独立的第一积分，形如

(σ=1,…,r)

(18)

证明由定义1，得到

ΔS=0

由公式(11)得

将方程(3)代入上式，并且考虑到εσ的独立性和积分区间的任意性，得到

积分之，即得到守恒量(18)。于是定理1得证。

定理2 对于El-Nabulsi动力学模型下的Birkhoff系统(3)，如果无限小群变换(4)是定义2意义下的Noether准对称变换，则系统存在r个线性独立的第一积分，形如

(σ=1,…,r)

(19)

证明由定义(2)和式(11)，并利用方程(3)式，且考虑到εσ的独立性和积分区间的任意性，可证明定理2。

定理1和定理2称为Birkhoff系统基于按指数律拓展的分数阶积分的变分问题的Noether定理。根据上述定理，可由El-Nabulsi动力学模型下的Birkhoff系统的Noether对称性找到相应的守恒量。当α=1时，定理1和定理2称为经典Birkhoff系统的Noether定理。

5 算 例

例设4阶Birkhoff系统的Brkhoff函数B和Birkhoff函数组Rμ为[20]

R1=a2+a3,R2=0,R3=a4,R4=0

(20)

试研究其基于按指数律拓展的分数阶积分的El-Nabulsi动力学模型下的Noether对称性与守恒量。

Noether等式(17)给出

(21)

方程(21)有解

ξ0=0,ξ1=1,ξ2=0,ξ3=0,ξ4=0,G=0

(22)

生成元(22)相应于所论系统基于按指数律拓展的分数阶积分的El-Nabulsi动力学模型下的Noether对称变换。根据定理1，得出相应的守恒量为

I=(a2+a3)(cosht-coshτ)α-1=const

(23)

当α=1时，守恒量(23)为标准Birkhoff系统的Noether守恒量。

6 结 语

基于按指数律拓展的分数阶积分的El-Nabulsi动力学模型，文章提出并研究了Birkhoff系统的Noether对称性与守恒量问题，建立了Noether定理。本文方法和结果具有普遍意义，可以进一步应用于各种约束力学系统，例如非完整非保守系统，机电耦合系统等。

参考文献：

[1]RIEWE F. Nonconservative lagrangian and hamiltonian mechanics [J]. Physical Review E, 1996, 53(2): 1890-1899.

[2]RIEWE F. Mechanics with fractional derivatives [J]. Physical Review E, 1997, 55(3): 3581-3592.

[3]AGRAWAL O P. Formulation of Euler-lagrange equations for fractional variational problems [J]. Journal of Mathematical Analysis and Applications, 2002, 272(1): 368-379.

[5]MALINOWSKA A B, TORRES D F M. Introduction to the fractional calculus of variations [M]. London: Imperial College Press, 2012.

[6]EL-NABULSI A R. A fractional approach to nonconservative Lagrangian dynamical systems [J]. Fizika A, 2005, 14(4): 289-298.

[7]EL-NABULSI A R. Fractional variational problems from extended exponentially fractional integral [J]. Applied Mathematics and Computation, 2011, 217: 9492-9496.

[8]EL-NABULSI A R. A periodic functional approach to the calculus of variations and the problem of time-dependent damped harmonic oscillators[J]. Applied Mathematics Letters, 2011, 24: 1647-1653

[9]EL-NABULSI A R, TORRES D F M. Fractional action-like variational problems [J]. Journal of Mathematical Physics, 2008, 49(5): 053521.

[10]EL-NABULSI A R. Fractional action-like variational problems in holonomic, non-holonomic and semi-holonomic constrained and dissipative dynamical systems [J]. Chaos, Solitons and Fractals, 2009, 42(1): 52-61.

[11]HERZALLAH M A E, MUSLIH S I, BALEANU D, et al. Hamilton-Jacobi and fractional like action with time scaling [J]. Nonlinear Dynamics, 2011, 66(4): 549-555.

[12]FREDERICO G S F, TORRES D F M. Constants of motion for fractional action-like variational problems [J]. International Journal of Applied Mathematics, 2006, 19(1): 97-104.

[13]FREDERICO G S F, TORRES D F M. Nonconservative Noether’s theorem for fractional action-like variational problems with intrinsic and observer times [J]. International Journal of Ecological Economics and Statistics, 2007, 9(F07): 74-82.

[14]ZHANG Y, ZHOU Y. Symmetries and conserved quantities for fractional action-like Pfaffian variational problems [J]. Nonlinear Dynamics, 2013, 73(1/2): 783-793.

[15]张毅. 相空间中类分数阶变分问题的Noether对称性与守恒量[J]. 中山大学学报：自然科学版, 2013, 52(4): 45-50.

[16]龙梓轩,张毅. 基于按正弦周期律拓展的分数阶积分的变分问题的Noether定理[J]. 中山大学学报：自然科学版, 2013, 52(5): 51-56.

[17]LONG Z X, ZHANG Y. Noether’s theorem for fractional variational problem from El-Nabulsi extended exponentially fractional integral in phase space[J]. Acta Mech, 2014, 225(1): 77-90.

[18]LONG Z X, ZHANG Y. Fractional Noether theorem based on extended exponentially fractional integral [J]. Int J Theor Phys, 2014, 53(3): 841-855.

[19]丁金凤，张毅. 基于El-Nabulsi动力学模型的Birkhoff力学 [J]. 苏州科技学院学报：自然科学版，2014，31(1)：24-28.

[20]HOJMAN S, URRUTIA L E. On the inverse problem of the calculus of variations [J]. J Math Phys, 1981, 22(9): 1896-1903.