基于Morlet小波尺度参数寻优的匹配追踪时频分析*

范兴利,成 谷,2

(1. 中山大学地球科学与地质工程学院，广东 广州 510275；2. 广东省地质过程与矿产资源探查重点实验室，广东 广州 510275)

对于地震信号这种典型的非平稳信号来说，传统的傅里叶分析方法不能完整地刻画其时变特征，需采用时间-频率的联合分析(时频分析)方式，将一维的时间信号映射到二维的时频平面，得到全面反映被观测信号的时间-频率联合特征。常用的时频分析方法有短时傅里叶变换(Short-Time Fourier Transform, 简称STFT)、连续小波变换(Continuous Wavelet Transform，简称CWT)、S变换(S Transform，简称ST)、广义S变换(Generalized S Transform，简称GST)、匹配追踪(Matching Pursuit，简称MP)方法等。

短时傅里叶变换也称加窗傅里叶变换，通过窗函数的加入对信号的局部特征进行分析。但由于采用固定的窗函数，存在两个明显的弊端：一是当分析包含两个以上的多分量信号时，很难使同一个窗函数同时满足几种不同的要求；二是窗函数的形状在移动过程中不能随时间发生改变。其实质是只具有单一分辨率，时频分辨率的高低取决于所选窗函数[1-5]。

连续小波变换继承和发展了短时傅里叶变换的局部化思想，引入了尺度因子，克服了短时傅里叶变换单一分辨率的缺点，窗口大小随频率变化，具有更高的时频分辨率，对信号具有自适应性[6]。但小波变换中尺度因子与频率没有直接关联起来，实际上是利用时间-尺度函数来分析非平稳信号，而不是严格的时间-频率的方式，结果不是真正意义上的时频谱；对于中等或者高频信号要想获得较高的频率分辨率，小波变换的方式并不高效。此外利用不同母函数进行小波变换分析信号时时常会得到不同的结论和效果，甚至出现无解的情况[6-9]。

S变换既可以看成是一种加窗的傅里叶变换，同时也可以看成是以Morlet小波为基本小波的连续小波变换。它结合了短时傅里叶变换和小波变换各自的优点，解决了短时傅里叶变换中不能改变分析窗口频率大小的问题，又引入了小波变换中的多分辨分析思想，同时与傅里叶谱保持着直接的联系。S变换较小波变换引入了相位因子，可无损恢复原始信号。但在S变换中，基本小波是固定的，这使其在应用中受到一定限制，在有些情况下不适用。广义S变换在S变换的基础上引入了两个调节参数对尺度与频率的关系进行调节，可灵活地调节高斯窗函数随频率尺度的变化趋势，加快或减慢时窗宽度随信号频率变化的速度，更好地适应具体信号的分析和处理[10-13]。

匹配追踪算法是由Mallat与Zhang首次提出的，本质是对信号进行稀疏分解[14]。与其它的时频分析方法相比，匹配追踪方法的时频分辨率最高，目前在噪声压制、油气检测及薄层识别等方面都有应用[15-17]。但匹配追踪传统的贪婪迭代算法计算效率相对较低，很多人致力于匹配追踪方法计算效率提高方面的研究。Liu等先后提出了基于Ricker小波和Morlet小波库的匹配追踪算法[18-19]，将地震信号的瞬时属性(瞬时振幅、瞬时相位、瞬时频率)特征引入到了匹配追踪算法当中，提高了算法的执行效率。张繁昌等采用基于信号瞬时包络和频谱分布双重控制的方法，得到了包含相位信息的高分辨率匹配追踪时频分布，后来提出了一种采用双参数动态扫描的快速匹配追踪算法[20-22]，进一步提高了匹配追踪的计算效率。邵君对基于MP的信号稀疏分解算法进行了研究[23]。Wang在Liu提出的基于Morlet小波库匹配追踪分解算法基础上，通过引入控制Morlet小波时宽、带宽的尺度参数，给出了三步法匹配追踪算法[24]，提高了算法的效率。本文探讨了以Morlet小波作为时频原子的匹配追踪算法中尺度因子对信号与时频原子匹配特征的控制作用，在此基础上进行了基于Morlet小波尺度参数寻优的匹配追踪时频分析。并利用模型数据测试了算法的准确性及在噪声压制、薄层厚度求取等方面的应用。

1 匹配追踪算法思想与流程

1.1 匹配追踪算法思想

匹配追踪算法的基本思想是：将原始信号投影到一系列时频原子上，即把原始信号表示为这些时频原子的线性组合，利用这些时频原子精确地表达原始信号。

时频原子这一抽象的概念，在具体实现过程中通常具化为由频率、相位、时延等参数确定的小波形态，Ricker小波和Morlet小波就是两种通常采用的时频原子形式。

从数学上表示，匹配追踪算法思想如下：设H表示希尔伯特空间，定义H中的一个时频原子库D，gγ∈D为时频原子库中的一个时频原子，是一单位长度的矢量，即数学上满足

‖gγ‖=1

(1)

对信号f(f∈H)，匹配追踪时频分析的思想是找到时频原子逐步最佳地表征信号的某一特征，数学上表述为将信号进行如下分解

f=〈f,gγ0〉gγ0+R1(f)

(2)

〈f，gγ0〉表示f与gγ0的内积，R1(f)表示用时频原子gγ0表示信号f所产生的误差。显然，gγ0与R1(f)是正交的，所以有

‖f‖2=‖〈f，gγ0〉‖2+‖R1(f)‖2

(3)

为了使残差能量‖R1(f)‖最小，须选择gγ0∈D使得‖〈f,gγ0〉‖最大。匹配追踪采用迭代算法，开始时设R0(f)=f，进行到第k次迭代时，上一步迭代的残差信号为Rk-1(f)，选择gγk∈D，使gγk与Rk-1(f)最匹配，即Rk-1(f)被分解为

Rk-1(f)=〈Rk-1(f),gγk〉gγk+Rk(f)

(4)

重复此分解过程，直到残差能量小于所设阈值，信号最终被分解为

(5)

将信号和时频原子抽象表示为高维空间中的矢量，则匹配追踪的算法思想可由图1表示。其中，带箭头虚线表示当前待分解信号，细实线表示针对当前待分解信号在时频原子库中找到的最佳时频原子，即在众多的时频原子中待分解信号在其上投影最大的一个(虚线所示矢量向细实线所示矢量投影值最大)，粗实线表示投影残差。上一步的投影残差作为下一步的信号(图1左侧的垂直虚线与图1右侧的垂直粗实线表示同一矢量)重复匹配过程。通常一个信号经有限次分解以后残差即可足够小，即匹配追踪算法的实质为稀疏信号分解。

图1 匹配追踪分解算法图示

1.2 匹配追踪算法流程

在匹配追踪算法中，时频原子形式和参数的确定是关键。对于时频原子中的相位、频率和时延等信息，通常通过希尔伯特变换确定。

匹配追踪算法具体流程如下：

1)将实地震道信号通过希尔伯特变换转换成复地震道信号；

2)寻找复地震道信号包络最大值处，此处的时间作为时间延迟u，瞬时频率作为频率参数ζ，瞬时相位作为相位参数φ；

3)以利用希尔伯特变换求得的时间延迟、瞬时频率、瞬时相位等参数作为待寻找的时频原子参数的初值，在其周围一定邻域内进行扰动构建多个时频原子，并将待分解信号向时频原子进行投影，对应投影值最大的参数即为寻找的最佳时频原子的参数。

4)从地震信号中减去上面生成的最佳时频原子的实部，并将剩余值作为新的地震信号；

5)重复步骤1-4，直到迭代误差小于阈值。

上述流程的第3步骤中，在计算机实现时通常需采用多重(循环的重数取决于时频原子的参数个数)循环的贪婪迭代寻找算法，因此计算效率相对较低。

2 基于Morlet小波尺度参数寻优的匹配追踪

在对地震信号进行匹配追踪时频分析时，主要采用Ricker和Morlet两种小波作为时频原子。Morlet小波在时域中的表达式为

(6)

其中，ζ是频率参数，u是时间延迟，φ是相位参数，σ是尺度参数。

以Morlet小波作为时频原子，其时频原子包括四个参变量，即γ=(σ,ζ,u,φ)，σ，ζ，u，φ分别表示时频原子中的尺度因子、频率因子、时间延迟和相位因子。

基于Morlet小波的匹配追踪算法将地震信号分解表示为一系列Morlet小波的线性组合。经过N次迭代，地震信号f(t)被分解成如下形式

(7)

其中，mn为在分解过程中与信号局部特征匹配最佳的Morlet小波时频原子，对应图1中绿线所示矢量，an为分解过程中信号向最佳时频原子mn投影值(图1中虚线向细实线方向投影值)大小，RN(f)为剩余量(图1中粗实线所示)，当达到阈值后可认为是噪声 。

在匹配追踪时频分析方法中，选取的时频原子应能很好地匹配信号的局部特征，分析时频原子中参数对信号特征的影响有重要的意义。在以Morlet小波为时频原子的匹配追踪算法中，Morlet小波中的尺度参数对于待分解信号向时频原子的投影能量具有重要的影响，因此本文对Morlet小波时频原子中的尺度参数对信号特征的影响进行了分析。

2.1 Morlet小波时频原子中尺度参数的作用

对一个连续的Morlet小波来说，尺度σ是一个重要的自适应参数，它控制着小波在时间域的宽度和频谱的宽度。图2所示是频率ζ=50，u=0.2 s，φ=0，尺度σ取不同值(1、1.5、2)时所对应的Morlet小波在时域和频域的展布情况，从图中可以看出，尺度取1、1.5、2时，信号时间域延续时间逐步加大，旁瓣个数增多幅度加大，频带宽度逐步变窄。即尺度取值较小时，Morlet小波具有相对较窄的时宽和较宽的频宽；当尺度取值较大时，Morlet小波具有相对较宽的时宽和较窄的频宽。因此，尺度参数对时频原子在时间域的形态具有较大的影响。

本文分析了匹配追踪算法中时频原子的尺度参数选取的准确度对投影(信号对时频原子的投影)能量的影响。在时频原子其它参数相同(频率为50 Hz、时延为0.2 s、相位为π/4)的情况下、以尺度参数为2的时频原子作为假想的信号，其它尺度参数为1到3之间以0.1为间隔的共21个尺度参数组成的Morlet小波作为时频原子与信号之间求取投影能量。发现尺度参数对投影能量的大小有较大的影响(见图3)。从图中可以看出，在其它参数均相同，仅尺度参数不同的情况下，不同的尺度参数得到不同的投影能量。在真实尺度参数2处，投影能量最强，越偏离真实尺度参数，投影能量越弱。由此可见：Morlet小波中的尺度因子对时频原子与信号的匹配特性具有重要的控制作用。由于尺度因子的引入，Morlet小波比Ricker小波更适合作为匹配追踪时频分析方法的时频原子。因此本文在进行匹配追踪算法设计时，采用Morlet小波作为时频原子的基本形式，并考虑到尺度因子对时频原子与信号局部特征匹配特性的控制作用，在对时频原子最佳参数确定时对尺度参数进行一维优先寻优迭代。

图2 尺度对Morlet小波在时频域展布的影响

2.2 基于Morlet小波尺度参数寻优的匹配追踪算法流程

基于Morlet小波尺度参数寻优的匹配追踪算法流程如下：

1)将实地震道信号通过希尔伯特变换转换成复地震道信号；

2)寻找复地震道信号包络最大值处，此处的时间作为时间延迟u，瞬时频率作为频率参数ζ，瞬时相位作为相位参数φ；

3)在固定其它参数情况下，对尺度参数进行-维寻优选代求取尺度参数σ，σ通过下式求得

(8)

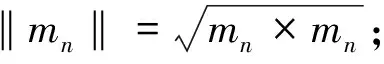
4)求取最佳振幅an

(9)

其对应的尺度参数即为最佳的尺度参数。

5)在求得的瞬时频率、瞬时相位、时间延迟、最佳尺度参数的基础上进行局部微调得到当前步骤最佳的时频原子。从地震信号中减去上面生成的时频原子的实部，并将剩余值作为新的地震信号；

6)重复步骤1-5，直到迭代误差小于阈值；

7)最后采用Wigner-Ville分布公式分别计算生成小波的时频谱，然后进行叠加，得到总的时频分布

(10)

式(10)中WVDmn(t,ω)是mn(t)的Wigner-Ville分布。

图3 时频原子的尺度参数与投影能量的关系

3 模型测试与分析

3.1 算法准确性测试

本文采用模型数据对基于Morlet小波尺度参数寻优的匹配追踪算法进行了测试。图4是用Ricker小波合成的一段地震记录。图中横向第1道数据包含两个频率为10 Hz、延时分别为0.2和0.9 s、相位分别为0和π/2的Ricker小波；第2道数据包含两个频率为20 Hz，延时分别为0.3和0.6 s，相位分别为0和π/2的Ricker小波；第3道数据包含3个频率为30 Hz，延时分别为0.7、1.1、1.15 s，相位分别为π/2、π/2和0的Ricker小波；第4道是上述所有小波(即前3道数据)叠加后的合成信号。图5是对图4中的合成信号采用基于Morlet小波尺度参数寻优的匹配追踪方法得到的几个时频原子，图中第1道是合成信号，从第2道到第8道是依次迭代得到的时频原子，第9道以后是7次迭代后的残差能量。从图中可以看出，组成合成信号的不同频率、延时和相位的ricker子波(表示信号中的局部特征)能很好地被Morlet子波时频原子匹配，充分体现了匹配追踪算法的稀疏信号分解本质。对图4中的合成信号分别进行短时傅里叶变换(STFT)、连续小波变换(CWT)、广义S变换(GST)、匹配追踪分解(MP)，得到四种时频分布，见图6所示。观察图中得到的四种时频分布不难发现，短时傅里叶变换时频分布效果较差，时间、频率分辨率都不佳，很难区分出各个小波，分别出现在0.6和1.1 s附近的两个小波不能被区分开，出现了“同时不同频率”的假象。相对短时傅里叶变换，小波变换和广义S变换得到的时频分布效果要好很多，时间和频率分辨率都较高，体现了多分辨率分析的优势，基本能够看出各个小波出现的时间以及频率。时频分布效果最好的是匹配追踪得到的结果，从图中可以看出，在0.2，0.6以及1.1 s附近，各自出现了两个相隔很近的小波，在小波变换和广义S变换图中，均出现了能量团“藕断丝连”的现象，而在匹配追踪时频图中可以看到这三个时刻出现的相隔较近小波都能够被很好的区分开，能量分布更为集中。由此可以看出利用匹配追踪算法进行时频分析的效果要优于短时傅里叶变换，连续小波变换以及广义S变换等传统时频分析方法。

图4 合成信号

图5 匹配追踪得到的时频原子

3.2 算法应用测试

采用基于Morlet小波尺度参数寻优的匹配追踪时频分析方法，本文针对模型对算法在去噪和薄层厚度求取等方面的应用进行了测试。

图7是利用基于Morlet小波尺度参数寻优的匹配追踪时频分析方法进行的去噪方面的测试。其中图7(a)图为不含噪音的合成地震记录，图7(b)图为加上高斯白噪声的含噪剖面。对含噪剖面中的每一道进行匹配追踪时频分析，给定误差阀值，得出对应每一道信号的重建信号和误差信号。将各道的重建信号排列在一起形成图7(c)，即为利用匹配追踪方法去除噪声的剖面，将各道的误差道排列在一起形成图7(d)，即为去除的噪声剖面。从图中可以看出，去噪效果较好。

图6 四种时频分析方法比较

图7 匹配追踪方法去除噪声

图8(a)是一楔形反射系数模型，一层砂岩楔形侵入泥岩空间，砂岩速度取为3 700 m/s，砂岩最大厚度100 m，一共有30道，采样间隔2 ms。利用反射系数模型生成合成地震记录。对合成地震剖面利用匹配追踪分解得到三维数据体，提取40 Hz的单频剖面如图8(b)所示。根据此楔形体模型薄层调谐厚度与振幅能量之间的关系，当薄层厚度为地震子波波长的1/4时，其振幅值最大，能量最强，这一厚度也称为调谐厚度。所以，利用单频剖面中的能量极值可估算对应该频率的薄层调谐厚度。对于40 Hz单频剖面而言，地震子波波长的1/4(即调谐厚度)为

(11)

式中，v是薄层砂岩体速度，f是单频剖面对应的频率，h是根据调谐理论计算出的对应该频率的调谐厚度。观察40 Hz单频剖面图，可以看出最强能量振幅出现在第7道，根据模型设置参数，30道对应厚度100 m，则第7道对应的厚度为

(12)

式中，h′是根据单频剖面计算出的振幅能量最强位置的薄层厚度，n是强能量振幅处道数，H是楔形体薄层最大厚度，N是总的地震道数。根据调谐频率计算出的调谐厚度与真实薄层厚度之间的误差量Δh为

Δh=|h-h′|=|23.12-23.33|=0.20 m

(13)

楔形体砂岩按道数的最小递变厚度Δh′是

(14)

对比Δh与Δh′，可以看出Δh≪Δh′，因此，估算误差是可以接受的，利用40 Hz单频剖面能够达到对该楔形体薄层厚度进行求取的目的。

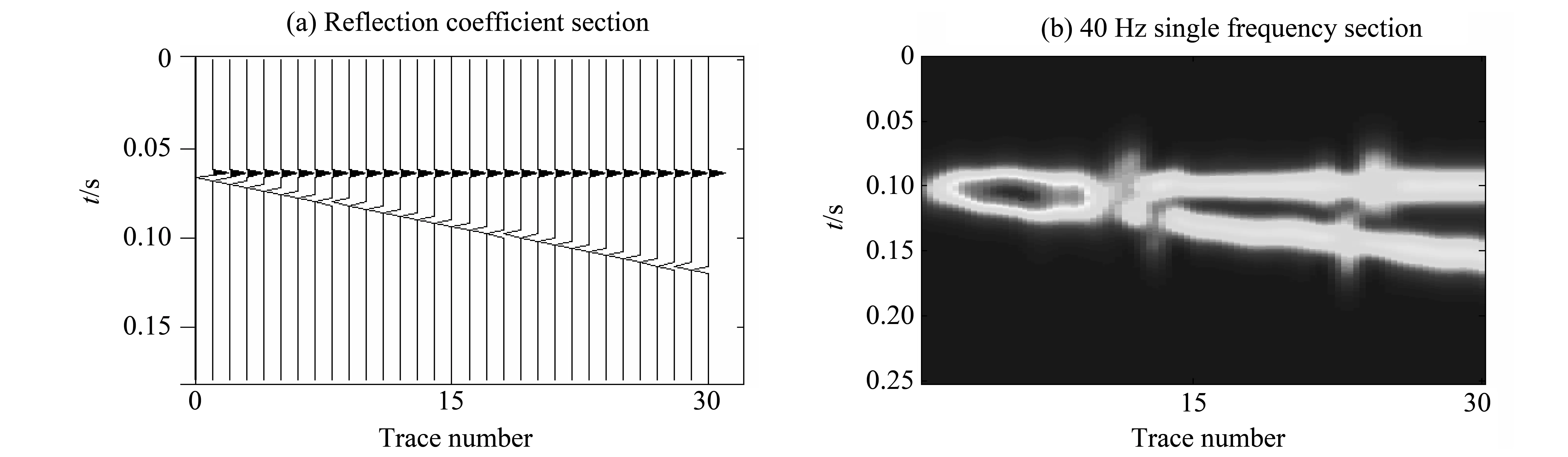
图8 匹配追踪方法求取薄层厚度

4 结 语

与短时傅里叶变换、连续小波变换、广义S变换等传统的时频分析方法比较，利用匹配追踪分解算法得到的时频分布具有更高的时频分辨率。匹配追踪时频分析方法本质上是对信号进行稀疏分解，将信号分解为多个时频原子的叠加。在算法实现过程中，通常采用Ricker子波和Morlet子波作为时频原子的基本形式建立时频原子库，然后在时频原子库中寻找与当前待分解信号局部特征匹配最佳的时频原子。时频原子库的建立是匹配追踪算法中关键的步骤，也是计算量消耗最多的步骤。传统的匹配追踪贪婪迭代算法在实现过程中需针对频率、相位、时延、振幅等多个时频原子参数采用多重循环迭代方式寻找最优的时频原子参数，算法效率较低。

本文对Morlet小波时频原子中的尺度因子对信号的时域形态和频域范围的影响进行了分析，分析结果表明：尺度因子取值较小时，Morlet小波具有相对较窄的时宽和较宽的频宽，尺度因子取值较大时，Morlet小波具有较宽的时宽和较窄的频宽。因此Morlet小波时频原子中的尺度因子对时频原子的时域形态具有重要的影响，进而将影响时频原子与信号局部特征的匹配特性(信号向时频原子投影的投影值大小表征时频原子与信号局部特征匹配特性的好坏)。在设定时频原子中其它参数(频率、相位和时延)相同，利用某一尺度因子生成信号，利用不同的尺度因子生成时频原子的情况下，本文计算分析了信号与不同尺度因子生成的时频原子的投影值大小，分析结果表明：在其它参数相同仅尺度因子不同的情况下，信号向时频原子投影的投影值不同。在真实尺度因子处，投影值最大。越偏离真实尺度因子，投影值越小。进而验证了尺度因子对时频原子和信号局部特征匹配特性的控制作用。

鉴于以上结论，本文在以Morlet小波作为时频原子进行匹配追踪算法实现时，首先利用希尔伯特变换获得时频原子频率、相位、时延等参数的初始值，利用这些初始参数值对尺度因子进行一维寻优。在寻找到最优的尺度因子后以其作为尺度因子的初值与其它参数一起进行局部微调，提高了计算效率。通过模型试算形象说明了匹配追踪算法的稀疏信号分解的本质，对算法在去噪和薄层厚度求取等方面的应用进行了模型测试，验证了算法的准确性。

参考文献：

[1]ALLEN J B，RABINER L R. A unified approach to short-time Fourier analysis and synthesis [J]. Proceedings of the IEEE, 1977, 65(11): 1558-1564.

[2]GABOR D. Theory of communication [J]. Journal of the IEEE, 1946, 93: 429-441.

[3]KOENIG W, DUNN H K, LACY L Y. The sound spectrograph [J]. The Journal of the Acoustical Society of America, 1946, 18(1): 19-49.

[4]边海龙. 非平稳信号联合时频分析方法的若干问题研究与应用[D]. 成都：电子科技大学, 2008.

[5]董建华，顾汉明，张星. 几种时频分析方法的比较及应用[J]. 工程地球物理学报, 2007(4): 312-316.

[6]吴勇. 基于小波的信号去噪方法研究[D]. 武汉：武汉理工大学, 2007.

[7]刘丽娟. 时频分析技术及其应用[D]. 成都：成都理工大学, 2008.

[8]吴伟龙. 基于小波变换的地震信号瞬时参数提取方法研究[D]. 大庆：东北石油大学, 2011.

[9]张贤达，保铮. 非平稳信号分析与处理[M]. 北京: 国防工业出版社, 1998: 446.

[10]姜镭. 基于时频谱特征的薄互层分析[D]. 成都理工大学, 2009.

[11]高静怀，陈文超，李幼铭,等. 广义S变换与薄互层地震响应分析[J]. 地球物理学报，2003, 46(4): 526-532.

[12]杨阳. 广义S变换时频分析的应用研究[D]. 哈尔滨：哈尔滨工程大学，2011.

[13]STOCKWELL R G, MANSINHA L, LOWE R P. Localization of the complex spectrum: the S transform [J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001.

[14]MALLAT S G, ZHANG Z F. Matching pursuits with time-frequency dictionaries [J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.

[15]CASTAGNA J P, SUN S, SIEGFRIED R W. Instantaneous spectral analysis: detection of low-frequency shadows associated with hydrocarbons [J]. The Leading Edge, 2003, 22(2): 120-127.

[16]孙万元，张会星，杜艺可. 匹配追踪时频分析及其在油气检测中的应用[J]. 山东科技大学学报：自然科学版,2011,30(4): 51-57.

[17]PARTYKA G, GRIDLEY J, LOPEZ J. Interpretational applications of spectral decomposition in reservoir characterization [J]. The Leading Edge, 1999, 18(3): 353.

[18]LIU J. Time-frequency decomposition based on Ricker wavelet [J]. SEG Technical Program Expanded Abstracts, 2004, 23(1): 1937.

[19]LIU J. Matching pursuit decomposition using Morlet wavelets [J]. SEG Technical Program Expanded Abstracts, 2005, 24(1): 786.

[20]张繁昌，李传辉. 非平稳地震信号匹配追踪时频分析[J]. 物探与化探, 2011, 35(4): 546-552.

[21]张繁昌，李传辉，印兴耀. 基于动态匹配小波库的地震数据快速匹配追踪[J]. 石油地球物理勘探, 2010, 45(5): 667-673.

[22]张繁昌，李传辉. 基于正交时频原子的地震信号快速匹配追踪[J]. 地球物理学报, 2012, 55(1): 277-283.

[23]邵君. 基于MP的信号稀疏分解算法研究[D]. 成都：西南交通大学, 2006.

[24]WANG Y. Seismic time-frequency spectral decomposition by matching pursuit [J]. Geophysics, 2007, 72(1): V13-V20.