导流板对桥墩周围紊动特性的影响

2014-03-22解刚伟沈小雄

水利水运工程学报 2014年2期

解刚伟，沈小雄，2

(1.长沙理工大学水利工程学院，湖南长沙 410114； 2. 湖南省水沙科学与水灾防治重点实验室，湖南长沙 410076)

水流经过桥墩，受到桥墩的阻碍作用使墩前流速急剧减小，一部分水流形成下潜水流与床面进行动量交换，形成马蹄形漩涡；另一部分水流直接在水平面上绕过桥墩，在桥墩尾部，两侧水流发生周期性分离，引起尾流漩涡。这两种漩涡及其释放出的更小尺度漩涡构成了桥墩绕流的综合水流结构，是导致桥墩底部床面冲刷和影响桥区通航安全的主要原因。为了桥区通航安全，《内河通航标准》[1]规定，确定通航净宽时必须考虑桥墩紊流宽度。

很多学者从减小绕流阻力的目的出发，研究消除涡街和抑制边界层分离的措施，如在圆柱尾部设置导流板。白桦等[2]模拟了圆柱尾部中轴线位置引入导流板的低雷诺数绕流情况；冯民权等[3]对导流板平面二维流速场和立面二维流速场进行数值模拟；贾兴豪等[4]用RNGκ-ε模型模拟计算了弯管内设置导流板后流体的流动特性；张群峰等[5]对二维圆柱层流绕流及其控制进行数值计算：以上研究结果均表明，导流板能很好地抑制圆柱表面涡脱在分离交界区的相互作用、改变流速场的分布。傅宗甫等[6]计算分析了异形孔桥墩附近河道的水流流动特征，得出异形孔桥墩对涡量有减小的作用。谢杰等[7]通过试验表明利用生涡器触发小尺度涡可抵抗流动分离的发生。

本文通过设置不同长度导流板控制桥墩绕流，在圆柱形和圆端形桥墩两种情况下，采用RNGκ-ε模型，计算分析有无导流板时桥墩周围的紊动强度，研究导流板控制绕流及对紊流宽度影响的效果。

1 基本原理及方法

通过对瞬态连续方程和Navier-Stokes方程时均化，得到直角坐标系下定常条件、不可压流体流动的控制方程。

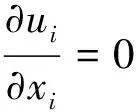
(1)

(2)

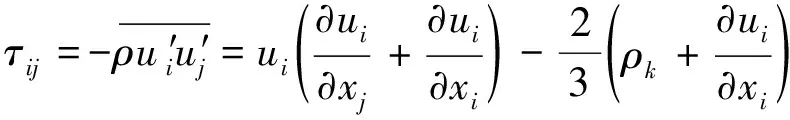
(3)

式中：δij为Kronecker 符号。采用两方程模型分别引入湍动能和耗散率方程。RNGκ-ε模型考虑大尺度运动和修正后的黏度项体现小尺度的影响，所得到的方程为：

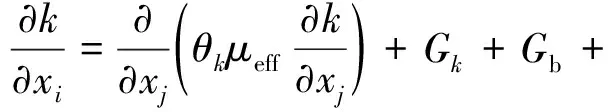
2 数值验证

2.1 网格条件及边界条件

计算区域为50D×20D(长×宽，D为桥墩直径)，圆柱距入口边界为10D；圆柱距出口边界为40D，上下边界距圆柱为10D，如图1(a)。计算网格采用六面体网格，圆柱区域网格集中加密(图1(b))。

(a) 计算区域 (b) 网格加密图1 计算区域及网格划分Fig.1 Computational domain and grid refinement

入口采用速度入口边界条件；出口采用自由出流边界条件；圆柱表面为无滑移边界条件，即速度相对无滑移、无穿透；计算区域的左右侧采用自由滑移边界；底部为壁面边界。

控制方程使用基于单元中心的有限体积法离散，离散格式采用二阶迎风格式，压力、速度耦合方程的解法采用SIMPLEC算法。

2.2 数学模型验证

图2 验证断面Fig.2 Verification sections

文献[8]对水流绕经圆柱体所形成的三维流体进行了研究。研究中物理试验采用长35 m、宽5 m的矩形水槽，水槽边壁光滑；试验圆柱体直径为53.6 cm，试验水深54 cm，行近流速为32.6 cm/s。研究认为雷诺数对马蹄形涡和壁面剪切应力影响很大，水流形态过渡到湍流马蹄涡时的雷诺数接近临界雷诺数，而壁面剪切应力随着雷诺数的增大而增大。

利用文献[8]的物理试验数据验证数学模型，所选择验证断面为圆柱体顺水流中轴线处，即图1所示x方向。测点位置距离圆柱壁2倍直径的范围内，不同深度的水平位置如图2所示。采用RNGκ-ε模型计算圆柱墩处流速(如图3)。数值计算的水平流速u在墩前位置与试验数据差别不大，墩后位置实测点的数据与数值计算结果相近，流速趋势分布一致。

(a) z=1 cm (b) z=5 cm

3 数学模型计算

3.1 计算条件

为研究不同墩型尾部设置导流板对紊动强度的影响，选择圆柱形桥墩和圆端形桥墩(如图4)，圆柱墩直径取D=5 m，相应导流板长度L取0.5D，1.0D，1.5D，设置于圆柱形桥墩顺水流方向的中轴线上，宽度t=0.1D；圆端形桥墩的端头、端尾直径取d=3.0 m，中间为2 m的矩形，即圆端形墩的长度方向为D=5 m，相应导流板长度L取0.5d，1.0d，1.5d，设置于圆端形桥墩顺水流方向的中轴线上，宽度t=0.1d。来流速度为2.5 m/s。

图5为计算圆柱形墩和圆端形墩紊流区紊动强度的断面位置，在墩柱沿x方向取11个断面，分别为-0.50D，-0.27D，0，0.27D，0.53D，1.01D，1.55D，2.04D，2.50D，3.00D和6.00D。每个断面沿y方向取若干密度的点来表示紊动强度在此处的走势情况。根据胡旭跃等[9]的试验研究，z方向水深H=0.883h附近的紊动强度值最大，所以取该水深断面。

图4 两种不同墩型图5 测量断面位置 Fig.4 Two different types of piers Fig.5 Positions of measuring sections

3.2 有无导流板时紊动强度的变化

3.2.1桥墩周围紊流区域的紊动强度图6为无导流板和设置导流板时桥墩周围X/D=-0.50～0.27断面范围的紊动强度值，圆形墩和圆端形墩在断面0D和0.27D紊动强度值较大，最大紊动强度较靠近Y/D=0.6的位置，而在断面X/D=-0.50～-0.27处，紊动强度无明显变化。

(a) 无导流板

(b) 圆柱墩

(c) 圆端形墩图6 有无导流板时桥墩周围紊动强度值对比Fig.6 Comparison of turbulence intensity values around the pier with and without diversion vanes

引入长度为0.5D，1.0D，1.5D导流板，圆形墩断面X/D=0～0.27处紊动强度有所减小，且导流板长度为1.0D比0.5D作用明显，在0D处最大紊动强度σ值由0.3降低至0.1，降幅比例增大50%，1.0D和1.5D导流板作用效果相差不大。对于圆端形桥墩，长度为0.5d，1.0d，1.5d导流板均能明显减小σ值，但3种长度作用效果差别不大。

3.2.2无导流板桥墩墩后紊流区紊动强度图7为无导流板时圆柱形桥墩和圆端形桥墩墩后紊流区紊动强度。由于漩涡的交替出现使得尾流区的紊动强度值在桥墩两侧出现峰值，圆柱形桥墩所测断面的最大紊动强度主要集中在Y/D=0.5～0.8的位置，至Y/D=1.2的位置以后，各断面的紊动强度值σ减小至0.1以下，其走势图呈现出先增大后减小的趋势。所测墩后的7个断面上紊动强度也是呈现先增大后减小的趋势，紊动强度最大值出现在X/D=2.04的断面上。由图可见，X/D=1.01～6.00断面之间是水流紊乱比较大的区域。

圆端形桥墩所测断面的最大紊动强度主要集中在Y/D=0.4～0.7的位置，至1.0D的位置以后，各断面紊动强度值σ普遍减小至0.1以下，总体呈先增大后减小的趋势。所测的7个断面上紊动强度也呈先增大后减小的趋势，紊动强度最大值出现在X/D=1.01～3.00的断面上。由图可见，X/D=1.55处是水流紊动比较大的区域。

(a) 圆柱形墩 (b) 圆端形墩图7 无导流板时圆柱形墩和圆端形墩墩后紊动强度Fig.7 Turbulence intensity values behind the cylindrical and the round-end piers without diversion vanes

3.2.3有导流板时圆柱形墩墩后紊动强度由图7(a)可知，墩后X/D=1.55～3.0断面之间的紊流效果明显，现通过比较断面1.55D，2.04D，2.50D和6.00D处设置有长度为0.5D，1.0D，1.5D导流板时的紊动强度，来判断导流板的控流效果(图8)。

从图8可见，在1.55D和2.04D处，3种长度的导流板对紊动强度有减小的作用；在2.50D和6.00D处，长度为0.5D导流板对减少紊动强度没有作用，而长度为1.0D和1.5D导流板对减少紊动强度作用明显，且对这些断面紊流控制的效果差不多。可见对于直径为5 m的圆柱墩，长度大于1.0D的导流板比0.5D的效果更佳，主要表现在整体紊动强度值明显减小，而且控流影响范围更大。

3.2.4有导流板时圆端形墩墩后紊动强度由图7(b)可知，墩后X/D=1.01～3.00断面之间的紊流效果明显。图9所示在断面1.01D，1.55D，2.04D和3.00D处，长度为0.5d，1.0d和1.5d导流板对紊动强度有减小的作用，且3种长度的导流板对这些断面紊流控制的效果差不多，紊动强度值均保持在0.1以下。

(a) 1.55D (b) 2.04D

(c) 2.50D (d) 6.00D图8 有导流板时圆柱形墩墩后紊动强度值比较Fig.8 Comparison of turbulence intensity values behind the cylindrical pier with diversion vane

(a) 1.01D (b) 1.55D

(c) 2.04D (d) 3.00D图9 有导流板时圆端形墩墩后紊动强度值比较Fig.9 Comparison of turbulence intensity values behind the round-end pier with diversion vane

3.3 紊流宽度的变化

以紊流强度的变化值σ=0.1[10]界定紊流宽度。根据图6(a)，无导流板时圆柱形墩周围紊动强度值σ>0.1的区域主要集中在X/D=0～0.27，Y/D=0.6～0.8断面之间，即Y/D=0.8为紊流宽度最大值。引入长度为0.5D导流板后，在X/D=0断面，最大紊动强度值由0.3减小至0.24，而设置长度为1.0D的导流板最大紊动强度值减小至0.12，但两种导流板对减小紊流宽度最大值则区别不大，σ=0.1的位置在Y/D=0.7断面处。在X/D=0.27断面，σ均减小至0.1以下，如图6(b)。根据图7(a)，无导流板时圆柱形墩墩后紊动强度值σ>0.1的区域主要集中在X/D=1.01～6.00断面范围内，Y/D=0.2～1.0断面之间，即Y/D=1为紊流宽度最大值。从图8可知，引入长度为0.5D导流板后，断面X/D=1.55和2.04处，最大紊动强度值有所减小，但各断面Y/D=1的位置，紊动强度值无明显减小，说明长度0.5D的导流板对减小紊流宽度效果不大。引入长度为1.0D导流板后，X/D=1.55和2.04两个断面，Y/D=1处的σ减小至0.1以下，在断面X/D=2.5和6.0的位置处，σ=0.1的位置存在于Y/D=0.8的断面处，即减小了20%紊流宽度值。导流板长度为1.5D的控流效果与长度为1.0D的相比差别不大。

根据图6(b)，无导流板时圆端形墩周围水流紊动强度值σ均在0.1以下。根据图7(b)，圆端形墩无导流板时X/D=1.01～3.00断面，σ>0.1的位置集中在Y/D=0.2～0.8，即Y/D=0.8为紊流宽度最大值。引入长度为0.5d导流板后，σ值均在0.1以下，且最大紊动强度值出现在Y/D=0.6，说明设置长度为0.5d导流板就能减小圆端形桥墩墩后紊流宽度。长度为1.0d，1.5d导流板作用和0.5d的相似，对减小圆端形桥墩墩后紊流宽度作用也相似。

4 结语

(1)在墩柱尾部中轴线位置引入导流板，水流紊流流态得到改善，从墩柱X/D=0断面开始至墩后X/D=6断面，墩柱紊动强度值呈减小趋势，且最大紊动强度值明显降低。而墩前X/D=-0.27，-0.5断面紊动强度值很小。

(2)无导流板的情况下圆端形桥墩最大紊动强度值出现的位置相对于圆柱形墩更靠近桥墩，且σ>0.1以上范围在Y/D断面分布较小。长度相同的桥墩，圆端形墩紊流区域的紊动强度在数值和范围上要比圆柱形墩的小。

(3)不同长度的导流板对同一墩型的作用不一样。圆柱形墩后长度为1.0D，1.5D的导流板作用比0.5D降低σ值更明显，能减小20%紊流宽度值。圆端形墩后长度为0.5d，1.0d，1.5d的导流板作用区别不大，均对减小紊流宽度有明显作用。

参考文献：

[1]GB 50139-2004，内河通航标准[S]. (GB 50139-2004， Navigation standard of inland waterway[S]. (in Chinese))

[2]白桦，李加武，夏勇. 低雷诺数圆柱绕流数值模拟及控制措施[J]. 建筑科学与工程学报， 2010， 27(4)： 39- 43. (BAI Hua， LI Jia-wu， XIA Yong. Numerical simulation and control measures of flow around circular cylinders at low Reynolds number[J]. Journal of Architecture and Civil Engineering， 2010， 27(4)： 39- 43. (in Chinese))

[3]冯民权，范术芳，郑邦民，等. 导流板的布置方式及其导流效果[J]. 武汉大学学报：工学版， 2009, 42(1): 87-91. (FENG Min-quan， FAN Shu-fang， ZHENG Bang-min， et al. Research on way to arrange vanes and efficiency of diversion[J]. Engineering Journal of Wuhan University， 2009, 42(1): 87-91. (in Chinese))

[4]贾兴豪，彭向和，龙血松. 导流板改善弯管流场的数值模拟与优化[J]. 西南大学学报：自然科学版， 2011, 33(3): 139-143. (JIA Xing-hao， PENG Xiang-he， LONG Xue-song. Numerical simulation and optimization of flow field in elbow pipes with baffle[J]. Journal of Southwest University (Natural Science Edition)， 2011, 33(3): 139-143. (in Chinese))

[5]张群峰，何鸿涛，吕志咏. 二维圆柱层流绕流及其控制数值模拟[J]. 科学技术与工程， 2009, 9(5): 1187-1193. (ZHANG Qun-feng， HE Hong-tao， LV Zhi-yong. Numerical study on two-dimensional laminar flow and control over a circular cylinder[J]. Science Technology and Engineering， 2009, 9(5): 1187-1193. (in Chinese))

[6]傅宗甫，赵春潮，安建峰. 异形孔桥墩附近河道水流流动特性[J]. 河海大学学报， 2011, 39(4): 402- 406. (FU Zong-fu， ZHAO Chun-chao， AN Jian-feng. Flow characteristics around bridge pier with special orifice[J]. Journal of Hohai University(Natural Sciences)， 2011, 39(4): 402- 406. (in Chinese))

[7]谢杰，许劲松，郁程. 圆柱绕流的流动分离控制[J]. 哈尔滨工程大学学报， 2011, 32(4): 401- 406. (XIE Jie， XU Jin-song， YU Cheng. A flow separation control on cylinder flow[J]. Journal of Harbin Engineering University， 2011, 32(4): 401- 406. (in Chinese))

[8]ROULUND A， SUMER B M， FREDSØE J， et al. Numerical and experimental investigation of flow and scour around a circular pile[J]. Journal of Fluid Mechanics， 2005， 534： 351- 401.

[9]胡旭跃，祖小勇，程永舟，等. 圆端形桥墩侧向紊流宽度的试验研究[J]. 水利水运工程学报， 2009(3)： 8-13. (HU Xu-yue， ZU Xiao-yong， CHENG Yong-zhou， et al. Experimental study of lateral turbulent flow width at round-ended pier[J]. Hydro-Science and Engineering， 2009(3)： 8-13. (in Chinese))

[10]何小花，陈立，王鑫，等. 桥墩紊流宽度的试验研究[J]. 水利水运工程学报， 2006(3)： 49-53. (HE Xiao-hua， CHEN Li， WANG Xin， et al. Experimental study of turbulent width at piers[J]. Hydro-Science and Engineering， 2006(3)： 49-53. (in Chinese))