城市轨道交通超大客流网络拥挤传播研究
2014-03-22,,
, ,
(1.西南交通大学 交通运输与物流学院,四川 成都 610031;2.中铁工程设计咨询集团有限公司 太原设计院,山西 太原 030009)
0 引言
准确把握轨道交通拥堵传播状态特性是轨道安全高效运营的基础,也是轨道交通应急管理的前提条件。由于轨道交通网络拥堵具有复杂性、随机性等特性,致使现有轨道交通网络拥堵研究一方面致力于轨道交通复杂网络不同拓扑结构如何影响网络运营动力并优化;另一方面致力于轨道交通运营管理研究,而在现今轨道交通运营过程中,管理部门多是根据现场经验,制定超大客流影响范围及其扩散速度。综合上述问题,如何在现有网络拓扑图结构下研究轨道交通网络拥堵,并制定运营管理策略成为了当今研究重点。如文献[1]建立了以乘客满意度和企业满意度加权平均值最大为总体目标的行车间隔时间优化模型,提高轨道交通运营质量;文献[2]以北京市地铁2号线建国门车站为背景,建立考虑车门宽度的乘客上车时间模型,通过上车时间的优化提高轨道交通的运营效率;文献[3]建立了站台列车交互模型,并利用遗传算法解决了给定车辆配置数时,于此确定列车发车时刻的最优方案以提高轨道交通运营质量。但上述研究仅从运营管理优化进行研究,均未考虑轨道交通拥堵网络传播特性及其影响范围。在网络运营条件下,某条线路的大客流通过换乘站辐射到其他线路上,形成了大客流的网络传播。这种现象与传染病在复杂网络上的传播相类似,因此本文借鉴经典的传染病仓储SIR模型描述该现象,模拟地铁网络受到超大客流影响的条件下,“客流拥挤车站”的数量变化,通过仿真获得其量化结果,为超大客流研究提供新的思路。机车运行分为上下行,以机车下行为研究对象进行模型建立。
1 城市轨道交通超大客流拥堵网路特性分析
城市轨道交通超大客流,是以线路、车辆、车站及其相关设备的能力为判定标准的相对概念。当客流量远超车站客运设施或客运组织措施正常情况下所能承担的客流量时,轨道交通的服务水平与安全度迅速降低,则定义为车站遭遇超大客流。其主要表现为:车站极度拥挤、客流速度减缓、客流交叉干扰严重。
超大客流经常在下面几种情况中出现:
(1)上下班早晚高峰时,早高峰集中在6:30—9:00,大量客流会涌入城市中心区,边缘车站乘客普遍乘车路段长,中心线路与换乘站压力极大,晚高峰出现在17:00—19:00,情况与早高峰相反[4]。
(2)沿线某站附近有大型活动或体育赛事时,该站到发客流量急剧上升,时间集中且持续较短,一般出现在活动开始、散场的前两小时,后一小时;客流出行目的一致而来源分散,具有高强度与高引发性[5]。
(3)节假日如十一黄金周、元旦、圣诞节等,由于城市核心功能区较为集中,使得商务、旅游等客流在节假日重叠,使地铁衔接火车站、景点与商业中心的车站遭遇超大客流,其峰值出现时间与早晚高峰不同且持续时间较长[6]。
(4)特殊恶劣天气时,地面交通受到较大影响,导致客流大量涌向地铁,造成突发特大客流。
(5)地铁设备设施故障,造成地铁运营中断,短时间内无法恢复正常运营,导致客流积压形成超大客流[7]。
城市轨道交通复杂网络具有典型的无标度特征,超大客流在网络上的传播符合流行病在非均匀网络上传播的规律,则结合传染病特性的网络传播模型的建立是可行的。
2 城市轨道交通超大客流拥堵网络疾病传播模型建立
2.1 数学符号的描述
经典的SIR模型将人群分为3类:易感人群、感染人群、免疫人群。对应的可将地铁网络中的站点按照受大客流的影响分为3类:受非本站超大客流影响的车站,用S表示;受本站大客流影响导致站台客流拥挤的车站,用I表示;被影响后恢复正常运营的车站,用R表示。λk表示当S类站点k与I类站点相邻时,拥挤状态从I传染到S的概率,λ的大小与站点自身有关,是一个动态变化的量;μl表示I类站点l由于客流到达减缓或运营组织方法调整恢复正常运营,变为R类站点的概率,同样的它也是一个因站点的不同而动态变化的一个量。用s(t),i(t),r(t)分别标记站点处于S态、I态、R态的密度,引入SIR模型,可以得到如下的超大客流传播模型
(1)
拥挤状态是否在车站之间传染,主要取决于列车承载能力与站台聚集人数的相对关系,以及站台最多可容纳人数的限制[8]。
2.2 超大客流集结模型
鉴于超大客流的特性分析,考虑到超大客流聚集成因,建立如下超大客流表达式
(2)

2.3 超大客流传染病传播模型
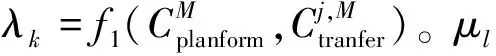

(3)
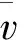
综合式(1)、式(2)、式(3)可得到车站的超大客流SIR传播模型
(4)
初始时刻s(0)=s0>0,i(0)=i0>0,r(0)=r0>0。上述方程组无法求出s(t),i(t),r(t)的代数解析解,利用方程组消去dt,令ρ=μ/λ为相对移出率,可得
(5)
方程组的解为
(6)
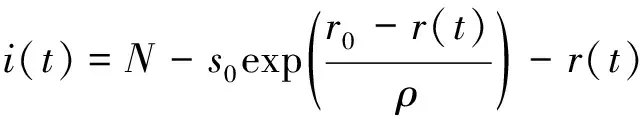

2.4 模型求解
考虑到数据之间的联系和求解精度, 运用Adams微分方程数值进行模型求解显式方法获得模型的数值解,该方法是多步求解微分方程的数值求解方法,能保证求解精度和求解过程的收敛性、稳定性[10]。
(9)

在网络传播的SIR模型当中,传染概率λ以及恢复概率μ有着至关重要的意义。在地铁大客流的传播分析当中,二者与客流状况、车辆状况、站点状况相关,是一个随时间、站点动态变化的量[11]。
3 仿真分析

图1 单一站超大客流网络传播仿真图
依据上述模型,探讨拥挤状况在城市轨道交通网络上的病态传递扩散特性以及恢复特性,探究单一站点或多站点的超大客流对轨道网络运营的影响程度。利用matlab软件,结合超大客流网络传播的SIR模型,对其进行仿真研究。网络节点中假设:N=40(表示轨道交通网络中的站点个数),在感染期间λ=1(轨道交通超大客流传染率),μ=0.3(轨道交通正常客流恢复概率)。其感染、健康、免疫分别用红、蓝、绿表示,如图1所示。
假设初始状态相爱I=4(表示轨道交通网络初期拥有超大客流的站点数)时,即初始有10%的车站北感染。在感染期间λ=1,μ=0.3。其感染、健康、免疫分别用红、蓝、绿表示。则其感染情况如图2所示。
(1)初始超大客流站点的单一,都可能在整个网络上造成拥挤扩散,造成网络上大量站点的拥挤,且传播速度快,时间短;经过一段时间后,拥挤站点逐步减少,这与病毒在无标度网络上的传播特性相符。表明在城市轨道运营管理中,即使是单个站点超大客流,也要对整个网络的运输组织工作进行全面协调,做好超大客流应急工作。

图2 多站超大客流病毒传播模型仿真图
(2)初始拥挤站点较多时,网络中其他站点经过拥挤状态以后,反而更快的恢复了正常,拥挤站点数下降较快。在图1、图2 的对比中可以看出,初始值I不同,图中所出现的超大客流感染时间不同、恢复时间不同。随着I值增大,即初始拥挤站点越大,对网络的影响时间持续越短。这反应了站点间客流极不均衡对网络运输的效率有消极影响。
4 结语
基于疾病传播模型,在分析轨道交通复杂网络的基础上,提出改进的超大客流的SIR模型,并运用Adams对模型进行求解。在运用matlab进行仿真时,针对不同初始拥堵站点值的设定,分析其传播特性。通过仿真对比,分析超大客流疾病传播在各种状态下特性。研究表明,拥堵传播率随初始拥堵站点数量增加而增加,网络恢复率与轨道运营管理有关。
参 考 文 献
[1]严波.城市轨道交通行车间隔时间优化模型研究[J].城市轨道交通研究,2008,12(6):53-57.
[2]曹守华,袁振洲,赵丹.城市轨道交通乘客上车时间特性分析及建模[J].铁道学报,2009,31(3):89-93.
[3]徐永实,徐瑞华.遗传算法在轨道交通发车时刻优化中的应用[J].城市公用事业,2011,4(2):27-29.
[4]曹启滨.基于地铁列车承载能力的套跑交路方案研究[J].科技传播,2011,11(7):33-34.
[5]侯永朋.广交会大客流下的地铁运营组织[J].都市快轨交通,2011,24(5):48-50.
[6]费安萍.大客流地铁运营组织[J].现代城市轨道交通,2005,6(2):33-35.
[7]代宝乾,汪形,陈娅.七京地铁大客流安全问题分析及对策研究[C]//中国职业安全健康协会2009年学术年会论文集.北京:煤炭工业出版社,2009:223-227.
[8]车宏安, 顾基发.无标度网络及其系统科学意义[J]. 系统工程理论与实践, 2004,21(4): 11-16.
[9]Pastor Satorras R,Vespignani A. Epidemicspreading in scale-freenetworks[J]. Phys Rev Lett, 2001, 13(86):3200-3203.
[10]孙胜秋. 用复杂网络理论研究疾病的传播[J]. 重庆师范大学学报:自然科学版 , 2005,25(22):1-5.
[11]熊众,王莉,李大卫,等. SIR传染病模型的参数反演[J]. 生物数学学报,2009,24(1):129-135.
