基于改进BP神经网络的铁路货运量预测
2014-03-22
(西南交通大学 交通运输与物流学院,四川 成都 610031)
0 引言
铁路货运量是国民经济发展和交通运输发展的重要经济指标,铁路货运量的预测对铁路建设、路网规划、资源配置和管理具有非常重要的指导意义和作用。由于影响铁路货运量的因素是错综复杂的,加之这些影响因素很难用数学语言来表达,所以就导致了预测模型的多样性和复杂性。传统的铁路货运量预测模型有:线性回归法、随机时间序列法、专家预测法、指数平滑法和状态空间法等,传统的预测方法和灰色模型预测法可以预测一段时间内货运量的大致变化趋势,但受不确定性因素,如环境因素、突发事件等的影响因素比较大,具有较强的波动性,因而对短期的货运量预测精度不高;现今的预测方法有:灰色预测模型法、神经网络模型法和支持向量机模型法等[1-4],支持向量机模型法的参数选取的的困难性一定程度上影响了其实用性。BP神经网络模型具有识别复杂非线性系统的特性,有良好的自适应、自组织、自学习能力,在一定程度上弥补了传统预测方法在非线性、不确定、时变系统预测上的不足,使预测更准确。
但标准的BP神经网络存在诸如收敛速度低、易陷入局部极小和网络训练对初始权值和阈值比较敏感等缺陷。因此改进BP网络模型的算法对于提高预测精度十分重要。标准的BP神经网络的学习率是固定值,选择太大会出现算法不收敛的情况;太小则会使训练时间过长[5-6]。标准的BP神经网络算法的权值最终会收敛到某一个值,但是并不意味着这个值就是误差平面的全局最小值,有可能是局部最小值[7]。文中运用改进的BP算法来克服这些缺点,以此来加快网络的训练速度和提高网络的输出精度。
1 改进的BP神经网络优化模型
标准的BP神经网络中激励函数的陡度因子是固定值,其函数的陡峭程度是固定不变的,此时不一定能得到较好的响应特征和非线性表达能力。改进的BP神经网络首先利用动态陡度因子来改变激励函数的陡峭程度,通过对陡度因子的调整来改善激励函数响应特征,得到更好的非线性表达能力,算法开始阶段以较小的陡度来避免网络陷入局部极小,并且逐步增加陡度来加快算法的收敛速度;其次,标准BP神经网络中输入层和隐含层之间的连接权值以及输出层和隐含层之间的连接权值的更新公式中没有动量因子这一参数,权值的改变无法把已有的学习经验融合进去,学习过程慢,改进的BP神经网络利用附加动量方法,累积算法以前的经验,加快学习过程的收敛[8];最后,标准的BP神经网络中学习速率是不变的、固定的,整个学习过程以固定的学习速率进行,网络学习的过程中容易产生振荡和收敛缓慢的问题。改进的BP神经网络把固定的学习率转变为变化了的学习率,避免过大的学习率使权值学习过程产生动荡,过小的学习率使网络收敛过慢。变化的学习率就是在初始阶段给定一个较大的学习率,随着学习过程的不断进行,学习率不断减小,最后网络趋向稳定[9]。改进的BP神经网络算法既可以得到更加准确的解,又可以在一定程度上缩短网络的学习时间。
改进BP网络模型的步骤:
步骤1:神经网络的初始化。由网络的输入X和输出Y确定输入层节点数m,输出层节点数n和隐含层节点数l;初始化输出层和隐含层之间的权值wij以及隐含层和输出层之间的权值wjk,隐含层的阈值a和输出层的阈值b;给定初始学习率lr和神经元激励函数。
步骤2:隐含层输出计算。利用输入X、隐含层阈值a和输入层和隐含层间的权值wij计算隐含层输出
(1)
式中,l为隐含层的节点数;f为隐含层的激励函数,文中所用的激励函数为S型函数,f=1/(1+e-x/p),其中,P为陡度因子,通过改变S型函数的陡度因子P来改变激励函数的陡峭程度。当P较大时,S型线较为平坦;当P很小时,S型线很陡峭;当P趋近于0时,S型线趋向阶跃。
陡度因子P的衰减方式影响着网络算法的准确性和速度。文中采用如下指数形式改进P的衰减
P=αtP0(2)
式中,P0为初始值,常数α∈(0,1];t为迭代次数。可以看出P为α的单调递减函数。当t变大时,P的下降速度变慢;当t变小时,P的下降速度变快[10]。因此,可以通过选取适当的α值来控制P的下降速度。文中,取α=0.85,P的初始值为P0=90,终止值为Pmin=0.1。

步骤4:预测误差的计算。利用网络的预测输出Ok和网络的期望输出Y计算网络的预测误差ek=Yk-Ok,k=1,2,…,m。
步骤5:学习率的改变。随着迭代次数的增加,学习率不断减小,当前学习率的计算公式为
lr(t)=lrmax-t(lrmax-lrmin)/tmax(3)
式中,lr为学习率;lrmax为最大学习率;lrmin为最小学习率;t为当前迭代次数;tmax为最大迭代次数。文中给定lrmax=0.15,lrmin=0.025,tmax=5 000。
步骤6:附加动量权值的改变。根据步骤4计算得到的网络预测误差e更新输入层和隐含层之间的连接权值wij及隐含层和输出层之间的连接权值wjk
(3)
wjk=wjk+lrHjek+λ(wjk-w(i-1)(j-1))j=1,2,…,l;k=1,2,…,m(4)
式中,λ为动量因子,取0.005 。
步骤7:隐含层阈值a和输出层阈值b的更新。根据步骤4得到的网络预测误差e来更新阈值a和b
(5)
bk=bk+ekk=1,2,…,m(6)
步骤8:根据迭代次数来判断算法是否结束,若没结束返回步骤2。
2 改进的BP神经网络在铁路货运量预测上的应用
铁路货运量的影响因素有:国民经济发展、产业结构变动、大宗货物产量、交通运输结构变动、对外贸易发展、国家政策等等;为了做定量分析,选取以下指标作为影响铁路货运量的因素:X1~X7分别为国内生产总值(亿元),第二产业比重(%),原煤产量(亿t),原油产量(万t),钢材产量(包含生铁,粗钢和钢材)(万t),粮食产量(万t),铁路份额(%);Y为铁路货运量(万t)。表1为各影响因素的原始数据[11]。

表1 各影响因素的原始数据
首先对数据进行归一化处理,待数据处理好以后,分别利用传统的BP神经网络模型和改进的BP神经网络模型对2012年和2013年的铁路货运量进行预测,以此来验证比较两种模型的优劣,见表2。

表2 2012年和2013年全国铁路货运量预测数据
图1和图2分别为传统的和改进的BP神经网络模型的仿真数据和原始数据的对照图。
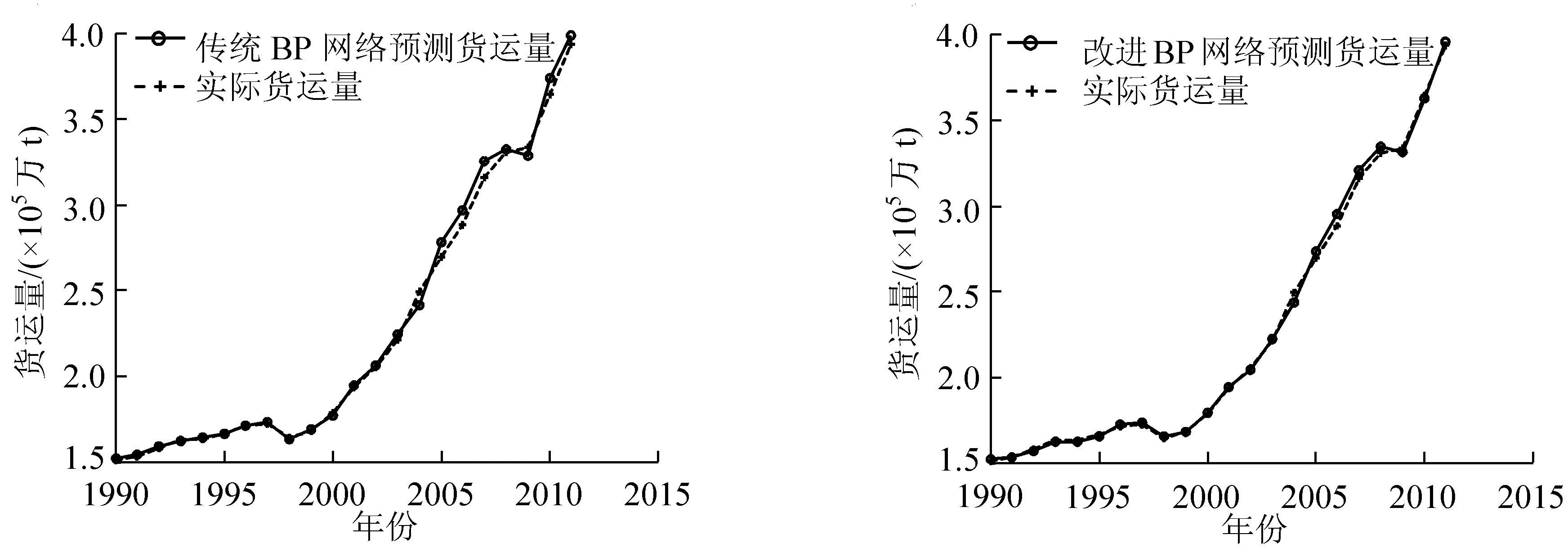
图1 传统BP神经网络模型原始数据与仿真数据对照图 图2 改进BP神经网络模型原始数据与仿真数据对照图
传统BP神经网络模型与改进的BP神经网络模型的比较:
(1)时间上。传统的BP神经网络模型算法的迭代次数为715次,改进的BP神经网络模型算法的迭代次数为289次,在速度上比传统BP算法提高了426次,在原来的基础上提升了59.6%,从此可知,改进的BP算法比传统BP算法收敛得速度更快。
(2)误差。传统BP神经网络的相对误差为3.18,改进的BP神经网络的相对误差为1.99,从此可知,改进的BP神经网络算法预测效果更好。
通过对传统BP算法和改进BP算法的比较可以得到如下结论:利用改进的BP神经网络模型算法对铁路的货运量进行预测是有效的,该算法相较于传统的算法在解的质量上有较大的提高,模型的精度高,收敛速度快。
3 结束语
从实际给出的算例可知,文中提出的改进BP神经网络算法对铁路货运量的预测是有效的,可行的,可以用来对铁路货运量进行预测。
参 考 文 献
[1]陈玉祥,张汉亚.预测技术与应用[M].北京:机械工业出版社,1985.
[2]曹星平,易东云.基于神经网络的时间序列预测方法进展[J].电脑与信息技术,1996(6):1-3.
[3]丁华福,宋宇航,唐远新.小波混沌神经网络的研究与应用[J].计算机技术与发展, 2011,21(8):64-65.
[4]Jacek M Z. Introduction to artificial neural systems[M].New York: West Publishing Company, 1992.
[5]Chen Fuchuang, Liu Chenchung. Adaptively controlling nonlinear continuous-time systems using neural networks[C]//Proceedings of the 1992 American Control Conference.Chicago: American Automatic Control Council,1992:46-50.
[6]周成当.BP神经网络与模拟退火法在测井解释中的应用口[J].测井技术,1993 ,17(5):339-343.
[7]陈琛,李旸,陈玮.基于BP神经网络的农业LED光源环境研究[J].计算机技术与发展,2011,21(9):1791-182.
[8]郭兰平,俞建宁,张建刚.基于改进RBF神经网络对股价的演变预测[J].兰州交通大学学报,2010,29(1):141-145.
[9]李季涛,杨俊峰.基于径向基神经网络的大连站客运量预测[J].大连交通大学学报,2007,28(1):32-34.
[10]伊力哈木·亚尔买买提,哈力旦·A.基于改进BP神经网络的人脸识别算法[J].计算机技术与发展,2010,20(12):130-132.
[11]中国交通年鉴编写组.中国交通年鉴2011[M].北京:中国交通出版社,2012.
