两交替运行部件冷贮备可修系统的可靠性
2014-03-22,
,
(石家庄铁道大学 数理系,河北 石家庄 050043)
0 引言
在实际生活和工程当中,有很多系统是两部件交替运行的冷贮备系统。比如在水厂用的抽水泵、医院用的氧气泵、还有瘫痪病人用的褥疮气垫、高层建筑当中使用的二次加压设备等,都是由两个或者两个以上的气泵等设备组成的交替使用的冷贮备系统。这些泵和设备每过一段固定的时间就做一次轮换,其目的就是为了提高系统的可靠性,由于部件的长期运行过程当中会产生一定的热量,而某些部件的失效率会逐渐随着温度的升高而逐渐增加,所以让部件轮流的休息散热和休息期间对部件进行适当维护可以有效的降低部件的失效率,从而达到提高系统可靠性的目的。然而在以往的研究当中,对于冷贮备系统的研究仅限于当一个部件损坏时,另一个部件才开始工作的情况,如文献[1-6],针对两个部件交替运行的冷贮备可修系统国内在数学层面的研究甚少,大部分的文献如[7-9]都是在技术层面,或者是在经验方面来研究该系统的,没有用一个确切的量化的数学模型进行研究。
本文对实际生活当中的两部件交替运行的冷贮备系统加以简化,建立可靠性模型,运用马尔科夫更新过程方法求出该系统的稳态可靠性指标。
1 模型假设
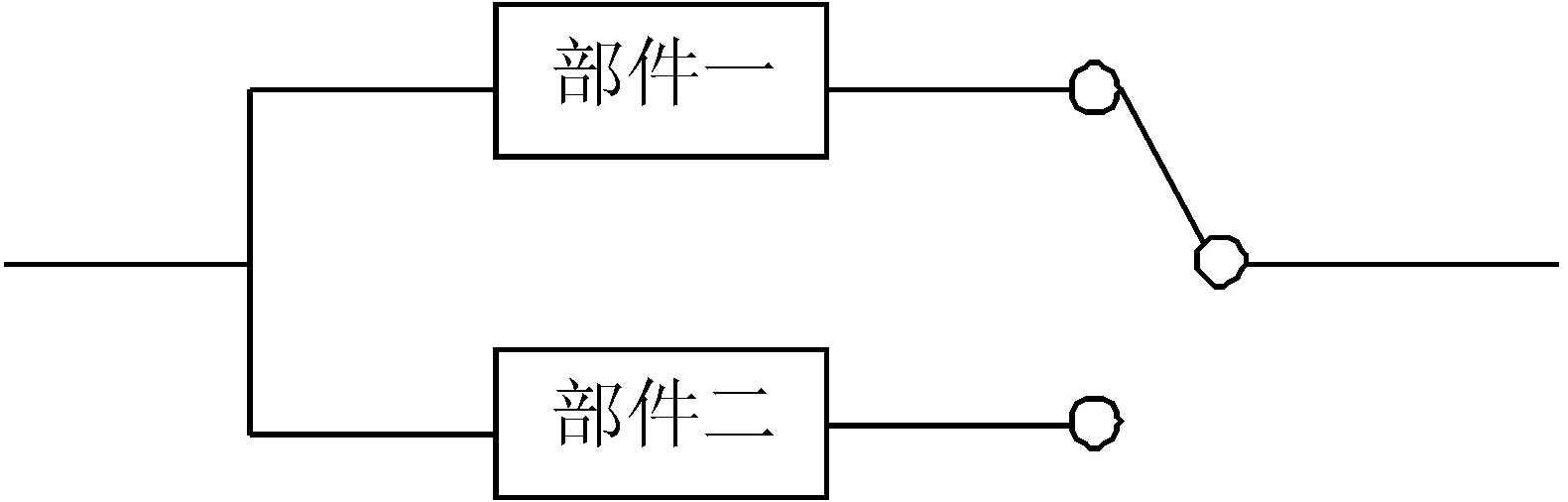
图1 系统可靠性框图
系统为两个部件组成的冷贮备系统,两部件寿命互相独立,系统的可靠性框图如图1所示。
1.1 系统假设
假设1 系统由两个同型部件和一个修理工组成。
假设2 系统在初始时刻两部件都是新的,一个部件先开始工作,另一个部件冷贮备,修理工空闲,当一个部件工作时间达到T时,另一个部件开始工作,原先工作部件开始进行维护,然后冷贮备,依次交替运行,当某一部件工作时间未达到T进入维修时,另一个工作部件工作,且不再计时直至有一部件修好,此时修好的部件开始运行,另一部件进行维护,然后冷贮备。
假设3 部件修复如新,部件维护也如新且维护时间忽略不计,开关转换是可靠的且转换时间忽略不计。
假设4 部件维修时间服从均值为μ,分布函数为G(t),密度函数为g(t)的一般分布,部件的寿命服从均值为λ,分布函数为F(t),密度函数为f(t)的一般分布。
1.2 系统状态假设
定义状态空间E={0,1},其中
状态0 系统一个部件刚开始运行,另一个部件冷贮备为进入0状态的时间。
状态1 系统中一个部件刚开始运行,另一个部件刚开始维修为进入1状态的时间。
状态2 系统中一个部件正在维修,另一个部件刚刚损坏为进入状态2的时间。
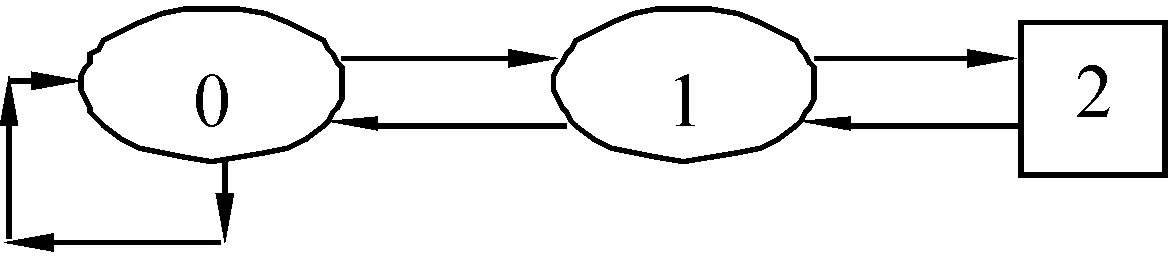
图2 系统状态转移图
其中进入状态2的时刻不是更新点,状态2是一个虚设状态。系统的状态转移图如图2所示。
2 系统变量假设与模型分析
(1)
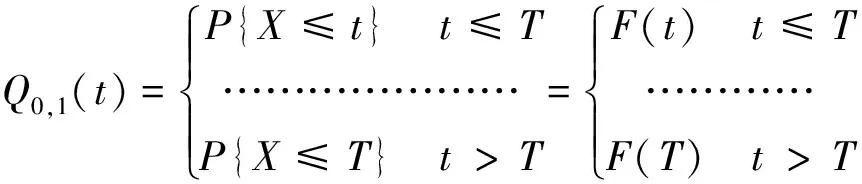
(2)
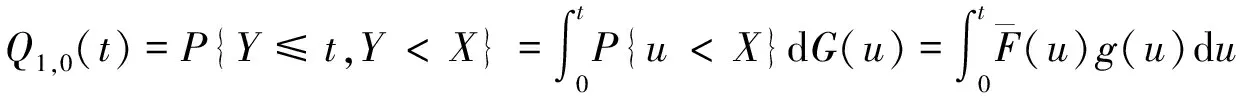
(3)

(4)
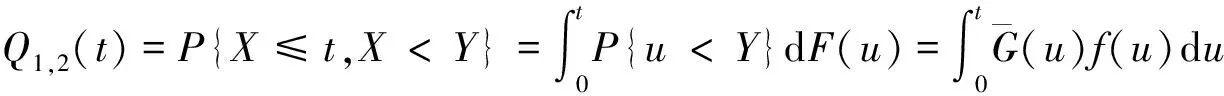
(5)
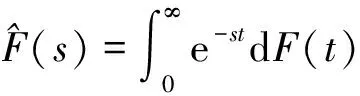
对式(1)至式(5)取L-S变换得
(6)
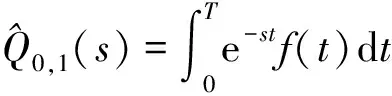
(7)
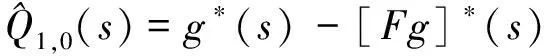
(8)
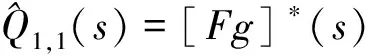
(9)
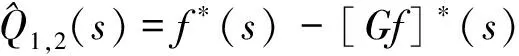
(10)
3 系统的可靠性指标
3.1 系统的首次故障时间
令Φi(t)=P{系统首次故障时间≤t|时刻0系统进入i状态},其中i=0,1。则由系统转移图可知Φi(t)满足下列更新方程组
(11)
对上述方程两端做L-S变换得
(12)
解得
(13)

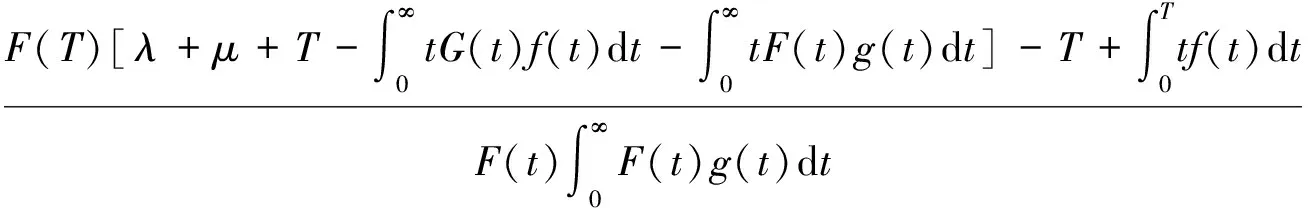
(14)
3.2 系统的稳态可用度
令Ai(t)=P{时刻t系统处于工作状态|时刻0系统进入状态i},其中i=0,1。则Ai(t)满足下列更新方程组
(15)
对上述方程做L变换得
(16)
解得
(17)
由马尔可夫更新过程极限定理以及L-S变换的托贝尔定理和洛必达法则可得系统的平均稳态可用度为
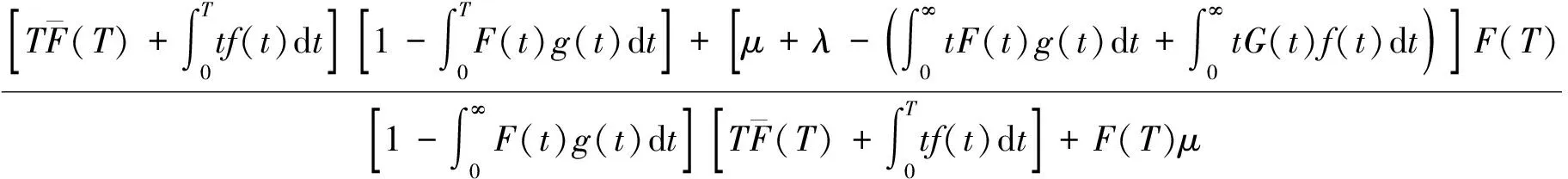
(18)
3.3 系统的稳态平均故障频度
令N(t)表示系统(0,t]时间内的故障次数,Mi(t)=E{N(t)|时刻0系统进入i状态},其中i=0,1。则Mi(t)满足下面马尔科夫更新方程组
(19)
将上述方程做L-S变换得
(20)
解得
(21)
由托贝尔定理以及洛必达法则,系统的稳态故障频度为
(22)
4 数值实例与分析
如果系统的各种参数为常数,部件交替时间间隔为 则易得到系统的首次故障时间、稳态可用度、稳态故障频度分别为I0(T),A(T),M(T),显然为T的一元函数。
假设系统中两部件的寿命均服从威布尔分布W(2,1,t),分布函数为F(t)=1-e-t2,密度函数为f(t)=2te-t2;系统部件维修时间分布也服从威布尔分布W(4,1,t),分布函数为F(t)=1-e-t4,密度函数为f(t)=4t3e-t4。
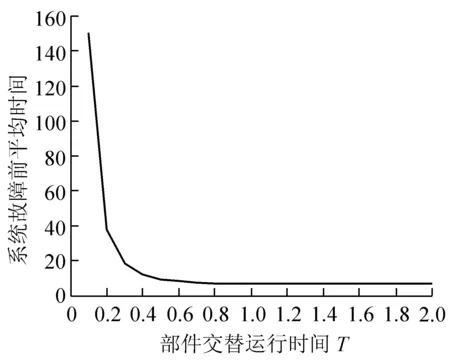
图3 系统故障前平均时间
将以上参数带入所求得的稳态可靠性指标表达式(式(14)、式(18)、式(22)),利用matlab工具进行计算,分别得到各个可靠性指标关于部件交替时间间隔 的函数图像,如图3所示。
由系统故障前平均时间的函数图像可知,系统故障前平均时间是随着部件交替运行时间间隔的增加而减小,这一点也是与实际相符的,因为随着运行间隔时间的增加会造成单个部件运行时间过长,从而导致失效率升高,进而导致系统故障前平均时间下降,但是由图像可以看出当T无限增大时系统故障前平均时间趋于稳定,这是由于当T→∞时,此时系统两部件不在做有时间限制的交替运行,而是直到一个部件故障时,另一个贮备部件才开始运行,这与一般的冷贮备系统还有一定的区别,就是当一个部件修好时不是直接进入冷贮备而是接替正在运行的部件继续运行,被替换下来的部件进行维护。此时系统与T不在有任何关系,所以造成系统故障前平均时间趋于稳定。
图4、图5分别是系统稳态可用度与系统稳态故障频度的图像。
从图4看系统的稳态可用度随着部件交替运行时间的增大而减小,最终趋于稳定,原因与图3情况相似。
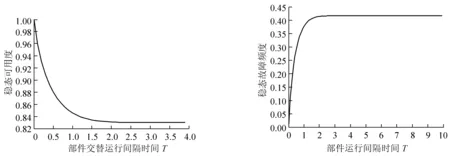
图4 系统稳态可用度 图5 系统稳态故障频度
由图5可知系统的稳态故障频度是随着部件交替运行时间的增大而增大的,原因与图4情况相似。
下面通过具体的数学计算来求出当T→∞时系统各个稳态可靠性指标趋于稳定的数值。由式(14)、式(18)、式(22),当T→∞时变为
(23)
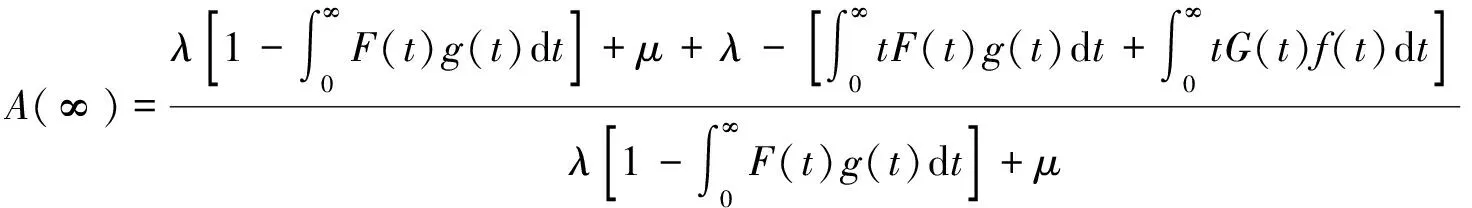
(24)
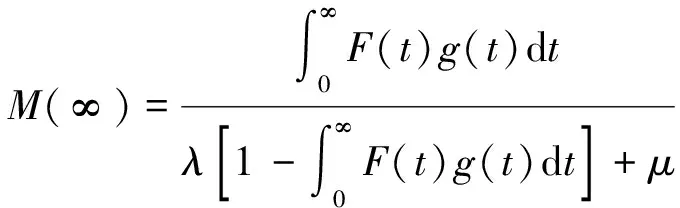
(25)
通过利用matlab工具进行数值计算可知,当T→∞时,系统各个稳态可靠性指标的稳定值为:I0(∞)=6.941 0,A(∞)=0.830 3,M(∞)=0.416 8,此数值与图像吻合,并且从(23)至(25)式中不难看出,当T→∞时系统的稳态可靠性指标与T无关,所以才从数值上趋于稳定。
5 结语
得到了系统的首次平均故障时间、系统稳态可用度、系统的稳态故障频度。通过理论推导与数值实例分析,画出图像验证了当T→∞时系统的稳态可靠性指标是趋于稳定的,并求出了系统稳态可靠性指标的稳定值。为在技术层面改进该系统的可靠性提供了一定的指导方向,对该模型在实际当中的应用提供了理论上的帮助,并且可以通过以上方法对该模型在不同参数下进行可靠性分析。
参 考 文 献
[1]曹晋华,程侃.可靠性数学引论[M].2版.北京:高等教育出版社,2006:266-279.
[2]Wu Qingtai,Wu Shaomin. Reliability analysis of two-unit cold standby repairable systems under Poisson shocks[J].Applied Mathematics and Computation,2001,218(1):171-182.
[3]苏保河.冷贮备可修系统的一个模型及其经济分析[J].数学的实践与认识,1996,26(4):351-356.
[4]刘仁彬,唐应辉.独立维修两不同型部件冷储备系统可靠性分析[J].系统工程学报,2006,21(6):628-635.
[5]王洪德, 马云东.基于冷储备可修模型的矿井主要通风机系统可靠性分析[J].煤矿安全,2003,34(6):2-3.
[6]Kit Nam Francis Leung, Yuan Lin Zhang, Kin Keung Lai. Analysis for a two-dissimilar-component cold standby repairable system with repair priority[J]. Reliability Engineering & System Safety,2011,96(11):1542-1551.
[7] 孟焕平.两台生活泵交替运行互为备用的控制电路探讨[J].建筑电气,2002(6):77.
[8]李绍秀, 彭勃.3池交替运行活性污泥法生物除磷脱氮的探讨[J].环境污染治理技术与设备,2004,5(5):81-83.
[9] 林凯.盘式除铁器交替运行功能的PLC设计[J]. 自动化与仪表,1999,14(3):52-56.
