带时间窗约束的道路危险品运输路径选择研究
2014-03-22
(西南交通大学 交通运输与物流学院,四川 成都 610031)
0 引言
危险品(Hazardous chemicals)是一种具有物理、 化学或是生物特性的物品,它容易在生产、储存、运输中引起燃烧、爆炸、中毒等灾害事故。随着工业的发展,危险品的生产量和运输量均在逐年增加。
在国外,危险品运输路径选择问题已经成了一个非常活跃的研究领域,引起了很多学者的关注。Current[1]等提出了一个双目标模型,最小化路径包括人口数和最小化行驶里程,产生连接于预先确定的OD组合权衡交换曲线。Abkowitz M和Cheng P[2]提出了一个考虑风险和成本的双目标路径模型,并综合风险与成本组成了一条对单个OD组合的Pareto最优路径。在我国,任常兴[3]构建了最小化运输事故概率和暴露人口风险模型,应用权数调整节点标号算法和边线标号算法解决危险品道路运输选线。王妍霞[4]综合考虑事故所造成的损失最小和运输成本最小时,运输方式和运输路径的选择方法。马昌喜[5]以运输风险、运营时间及敏感目标人数最小化为目标,建立了危险品公路运输路径多目标决策模型,然后用扩展标号法[6]计算最优折衷解。
纵观国内外现状可知,目前在危险品配送网络路径选择研究中已经取得了一些成果,但现有研究成果忽略了危险品运输过程中的动态性,即没有考虑危险品在道路运输的消耗时间随时段的不同而改变,以及时间窗的约束。本文将在时间窗和运输时间动态变化的条件下,研究危险品运输路径的优化选择。
1 优化模型
研究的问题描述如下:在一个城市道路运输网络中,假设每种运输方式在各路段上发生事故的概率以及事故所造成的损失已知,各路段上不同时段的危险品的运输时间已知。现有多种流向的危险品要从相同的起讫点运输到不同的终点,每一个OD之间都有多条运输路径可以选择,在综合考虑运输社会总期望损失和运输成本的情况下,如何确定各种流向危险品的运输路径。
1.1 模型假设
为降低运输成本和仓储成本,明确层次和关系以方便管理,对于危险品配送网络来讲,一般有如下要求:
(1)为了方便网络中危险品配送的运输,所有危险品必须从起讫点发出,目标节点相互间不存在危险品的调配运输。
(2)各个OD的危险品的运输量由其目标节点所在的地的需求量决定,而且危险品到达仓库时需满足其时间窗的约束。
(3)为了简化研究问题,假设网络中只有一种危险品需要运输,且同一流向危险品的运量在某两节点之间不能分割。
1.2 抽象描述
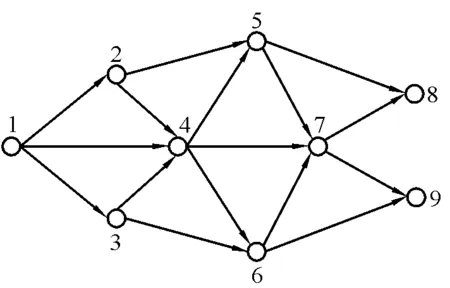
图1 现代危险品物流配送网络
在建立优化模型前,首先对运输网络G=(V,E,R)的拓扑结构进行抽象描述,其中,V表示节点集合,E表示有向弧集合,R表示弧的权重集合。将图中的节点和连接这些节点的道路分别类比为网络中的顶点和有向弧,某城市物流运输网络简图如图1所示。
顶点集V包括危险品运输网络中的起讫点、转运节点以及目标节点,所有OD流向的首末节点表示运输网络中的起讫点与目标节点,其余节点即为运输网络中的转运节点;有向弧E为起讫点、转运节点以及目标节点之间的连接弧;弧权重R包括危险品通过该路段所造成的风险R1、影响人数R2以及消耗时间R3。
1.3 符号说明
(1)已知常量。令f表示网络中危险品的某种流向,o(f)为第f种危险品流向的起讫点,d(f)为第f种危险品流向的目标点,所有流向的集合即为F,即f∈F;plf表示第f种流向的危险品在网络G中的第l条可选路径,各条路径的集合记为Pf,即plf∈Pf;rij表示危险品在路段(i,j)上运输的事故发生概率;Qij表示路段(i,j)上暴露的人口数量;tij表示在危险品通过路段(i,j)所消耗时间;[T1f,T2f]表示第f种危险品的送达时间窗约束,T1f为最早送达时间,T2f为最晚送达时间;
(2)决策变量。xijf为0-1变量,表示f流向危险品是否通过路段(i,j),取1时为是,取0时为否。
1.4 模型建立
在危险品运输过程中,整个路网中发生事故的总期望为
(1)
整个路网中危险品运输所影响的人数为
(2)
因此,在时间窗约束条件下,构建危险品储运一体化的优化模型如下:
(3)
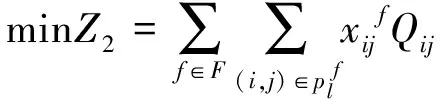
(4)
xijf∈{0,1}
(5)
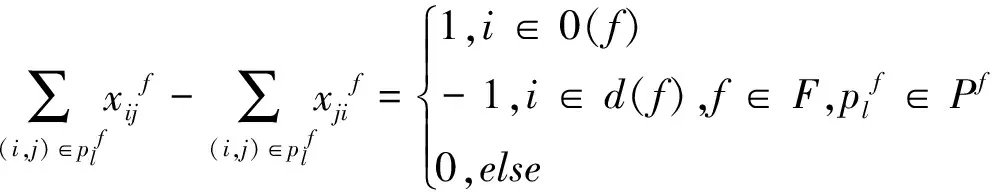
(6)
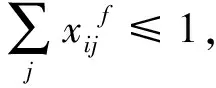
(7)
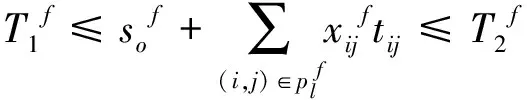
(8)
上述优化模型中,目标函数(3)表示整个路网中发生事故的总期望最小,目标函数(4)表示整个路网中危险品运输所影响的人数最少;约束条件(5)表示决策变量取整数变量0或1,即货物运输过程中不能分割,同一流向危险品的运输路径相同;约束条件(6)表示用于保证危险品在节点运输的方向性和流平衡;约束条件(7)表示危险品两节点间只能选择一条路径;约束条件(8)表示某种流向的危险品满足目标节点的到达时间窗约束,即危险品不能早于目标节点的最早送达时间,且不能晚于最晚送达时间。
2 模型求解
由于模型的求解难度随着路网的复杂程度增加而呈几何级数上升,具有NP-hard的特性,本文设计了基于蚂蚁系统(AS)[7]的搜索策略,所有蚂蚁从起讫点O出发,在危险品运输路网中寻找第一个流向f1的优化路径,蚂蚁完成路径的构建后,重新回到O点搜索第二个流向f2的优化路径,直至所有目标节点都出现在路径中。
算法的重要步骤设计如下:
(1)用层次分析法确定权重w=(w1,w2),并选择合适的加权开方乘方平均数Pw(α)将危险品公路运输路径多目标决策模型中的目标函数表示单目标函数。
(2)算法初始化。设置信息素重要系数α,启发式信息重要系数β,信息素蒸发系数ρ,信息素增强系数P,最大迭代次数Ncmax,蚂蚁个数m,路段启发式信息计算公式η(i,j)=1/w1rij+ηw2Qij,信息素τij←τ0,当前迭代次数Nc←0。
For k=1 to m
将所有蚂蚁置于起讫点O,时间timeok←Sk(0)
End for
(3)解的构造。
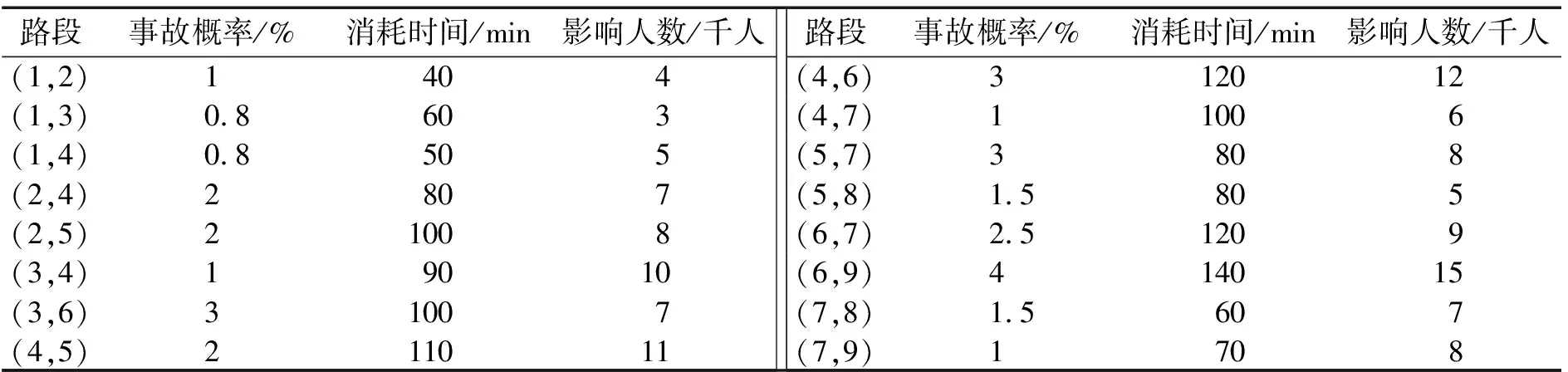
WhileNc For k = 1 to m While 蚂蚁游历的节点中不包括第一个流向f1的目标节点D1 对蚂蚁k判断下一个要到达的节点j是否满足可行的约束条件: ①未被访问过:节点j∉蚂蚁的记忆表Tabu(k); ②满足到达节点j的时间timeok≤目标节点D1的时间窗上限T2D1 If 存在可行节点 按照如下概率转移公司选择下一节点j; Tabu(k)←[Tabu(k),j],timejk←timeik+tij End if End while While 蚂蚁游历的节点中不包括第二个流向f2的目标节点D2 …… While 蚂蚁游历的节点中不包括第m个流向fm目标节点Dm …… End while 按照下式更新信息素 记录本次迭代中最优路径的蚂蚁 当前迭代次数Nc←Nc+1 End while 为实现上述算法步骤,可以通过一些具有高级程序语言编译功能的计算软件如Matlab7.0进行求解。 下面给出一个简单的算例,危险品运输网络如图1所示,其中,V1=1表示危险品的输出节点,V2=(2,3,4,5,6,7)表示危险品运输网络中的转运节点,V3=(8,9)表示危险品运输的目标节点。运输网络中存在1→8、1→9两种危险品流向,两种流向的危险品送达时间窗约束分别为[9:00,11:00],[11:00,12:00]。危险品出发时间为早上6:00。 危险品在不同路段的事故发生概率和运输消耗时间如表1所示。 表1 各条路段的事故概率、消耗时间及影响人数 按前文所述模型算法进行计算,得到结果如表2所示。 表2 各流向危险品路径选择结果 在探讨现代危险品配送网络模型特点的基础上,提出了带时间窗约束的多流向危险品配送模型,给出了求解算法和过程,最后以实例证明该模型的可行性。本模型在时间窗约束条件下对整个危险品运输网络进行优化,对危险品的运输管理工作具有现实的指导作用。 参 考 文 献 [1]Current JR. The minimum-covering shortest-path problem[J]. Decision Science, 1988,19:490-503. [2]Abkowtiz.M and Cheng P. Developing a risk-cost frame work for routing truck movement of hazardous materials[J]. Accident Annual Prevent, 1988,20:39-51. [3]任常兴,吴宗之. 危险品道路运输选线问题分析[J].安全与环境学报,2006,6(2):84-88. [4]开妍霞,王海燕. 危险品运输网络中运输方式和路径优化研究[J].中国安全生产科学技术,2009,5(1):37-41. [5]马昌喜,广晓平. 发达运输网络环境下危险品公路运输路径决策[J].交通运输系统工程与信息,2009,9(4):134-139. [6]《运筹学》教材编写组. 运筹学[M].北京:清华大学出版社,2005. [7]Marco Dorigo. 蚁群优化[M].北京:清华大学出版社,2006.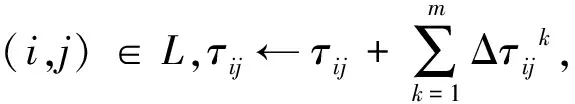
3 实例分析

4 结束语
