船闸闸首横向荷载及不平衡剪力分配方法

何良德1，，刘江林，何英发，许可

（1.河海大学海岸灾害及防护教育部重点实验室，江苏 南京 210098；2.河海大学港口海岸与近海工程学院，江苏 南京 210098）

船闸闸首横向荷载及不平衡剪力分配方法

何良德1，2，刘江林2，何英发2，许可2

（1.河海大学海岸灾害及防护教育部重点实验室，江苏 南京 210098；2.河海大学港口海岸与近海工程学院，江苏 南京 210098）

为提高闸首底板分段法的计算精度及其适用范围，针对规范中横向荷载分配方法的不足，在深入分析边墩横向荷载扩散传递机理的基础上，提出并列铰接悬臂梁法；并首次进行横向整体平衡分析，给出横向不平衡剪力的分配方法。结合工程实例计算，证明横向荷载分配之后进行内力调整的必要性。提出的2结点并列悬臂梁法，能够考虑边墩高度的影响，并反映横向荷载、弯矩分配比例不同的特征。对于承受横向不对称荷载的闸首，还应进行横向不平衡剪力计算和分配。与有限元结果比较分析表明，经横向荷载分配、横向不平衡剪力分配、内力调整后，底板内力计算结果有较高的精度。

航道工程；船闸；并列悬臂梁法；横向荷载分配；横向不平衡剪力；内力调整

0 引言

闸首是由边墩、底板组成的几何轮廓不规则的U型结构，其承受的荷载很复杂，除有竖向荷载外，还有横向荷载和纵向荷载，故其内力计算属空间问题[1]。为简便计，常将空间问题简化为平面问题，采用规范推荐的分段截条成梁法[2]计算底板内力，主要步骤包括：①闸首底板的纵向分段；②竖向不平衡剪力计算及分配；③边墩横向荷载的分配；④各段底板内力计算；⑤内力调整等。

目前的分段法通过考虑竖向不平衡剪力反映各特征段之间的相互作用，将横向荷载合理地分配到各特征段上，在各段内力计算后，为了更好地考虑底板的整体工作，最后对内力进行调整。

1）基于侧向弯曲扭转变形的横向荷载分配方法[2]仅适用于高水头船闸，而且只能考虑荷载高度的影响，不能考虑荷载作用范围以上边墩高度的影响，也不能反映出横向荷载、横向弯矩传递分配的差异。

2）横向荷载分配仅仅是反映了边墩的整体作用，使得边墩底与底板顶截面处受力更接近实际情况，未及考虑分段底板之间的整体作用。因此，船闸规范的“经横向荷载先行分配，计算求得的各特征段内力，则不再进行内力调整”[3]规定，是值得斟酌的。

3）常规的分段法适用于闸首结构横向对称、荷载横向对称的情况，在分段面上不会产生横向不平衡剪力。船闸在水利枢纽中通常靠岸布置，下闸首的临水侧无回填土、靠岸侧有回填土且填土高程沿纵向变化可能较大，下闸首横向不对称受力状态明显[4-5]。因此，横向不平衡剪力分配及其对内力的影响，值得进一步深入研究。

本文在深入分析横向荷载扩散传递机理的基础上，提出并列铰接悬臂梁法；进行了横向整体平衡分析，给出了横向不平衡剪力的分配方法。结合工程实例计算，证明了横向荷载分配之后进行内力调整的必要性。实例表明，经过横向荷载分配、横向不平衡剪力分配、内力调整后，各特征段底板内力有较高的计算精度。

1 边墩横向荷载分配

边墩承受横向荷载时，由于边墩的整体作用，荷载自上向下扩散传递到底板的一定范围内，而使直接受荷部位实际承受的弯矩减少。因此，对于边墩较高的整体式闸首，可将沿纵向分布变化较大的横向荷载先行分配于各特征段上，然后进行各特征段底板内力的计算[2]。

1.1 规范法

由于横向压力沿闸首长度方向分布不均匀，而使边墩发生侧向弯曲扭转变形[2]。横向压力沿闸首长度的分配，可按边墩承受的横向压力与截面受扭所产生横向变形Δa，Δb成正比的假定求得，如图1所示。

图1 横向荷载作用下边墩的位移（平面图）Fig.1 Displacement of lateral load on side piers（floor plan）

式中：P0为作用在一侧边墩上横向力总和，kN； B0为边墩长度，m；Pa，Pb为闸首边墩上、下游端面经分配所得横向压力强度，kN/m；Δa，Δb为闸首上、下游端的位移（横向合力作用点高程处端面），按均匀材料的边墩在横向力作用下的弯扭变形公式（3）求得。

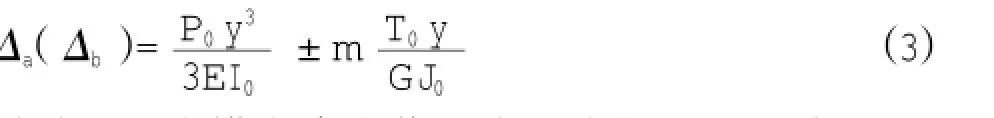
式中：y为横向合力作用点至底板顶面距离，m；E为混凝土弹性模量，kPa；I0为边墩惯性矩，m4；m为边墩形心至上游或下游端面的最大距离，m；T0为一侧边墩承受的扭矩，为横向合力与形心距离的乘积T=P×e，kN·m；G为混凝土剪切模量，kPa；J0为边墩扭转时的惯性矩，m4。

边墩扭转时惯性矩J0计算式[6]为：

式中：a，b分别为取边墩截面（B×L1）的长边、短边，m；β2为因子，与截面的长宽比有关，可查表1。

表1 矩形截面杆扭转时因子β1，β2Table 1 β1and β2factors for the torsion of rectangular cross-section bar

假设边墩上游侧一般长度范围内有竖向三角形分布荷载，有以下近似条件：

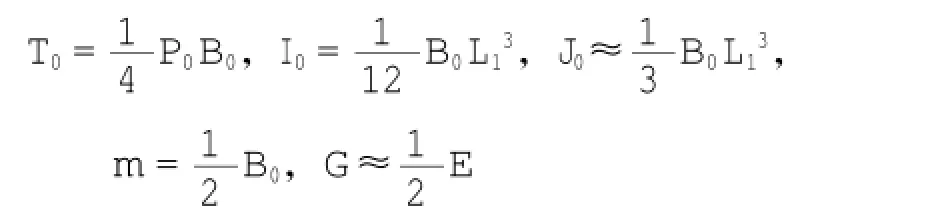
代入式（4）得：

上式说明y≤0.43B0时，也就是荷载高度3y或边墩高度H2≤1.30B0时，Δb≤0可能导致分配的荷载不合理。因此，式（3）的分配法一般只适用于高水头船闸。

1.2 规范法改进

规范的横向荷载分配方法实质是假设边墩为固结于底板上的细长悬臂梁，而闸首的边墩长度、厚度、高度尺寸在同一量级，剪切变形项不可忽略[7]。故式（3）可改进为：

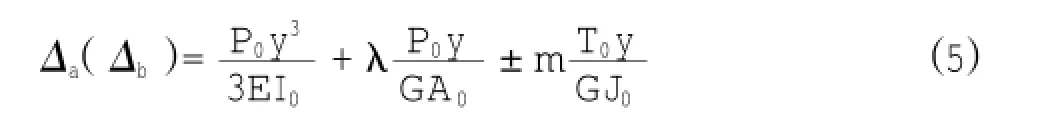
式中：λ为考虑剪应力分布不均匀性的修正系数，与截面的形式有关，如矩形截面λ=6/5；A0为边墩截面面积，m2。

1.3 并列铰接悬臂梁法

针对规范法存在的不足，本文根据荷载传递分配机理提出了并列铰接悬臂梁法。

闸首边墩纵向长度B0、横向宽度L1、高度H2，根据底板的分段原则，可将边墩对应划分成m段，各段宽分别为b1，b2，…，bm，成为m根并列悬臂梁，有m-1个梁间截面，如图2所示。考虑到影响横向力分配的主要因素，假设并列悬臂梁之间侧向铰接，在梁间第i个截面上（i=1，m-1）分别有n个等间距分布的横向剪力Qi，k（k=1，n），共有n（m-1）个。

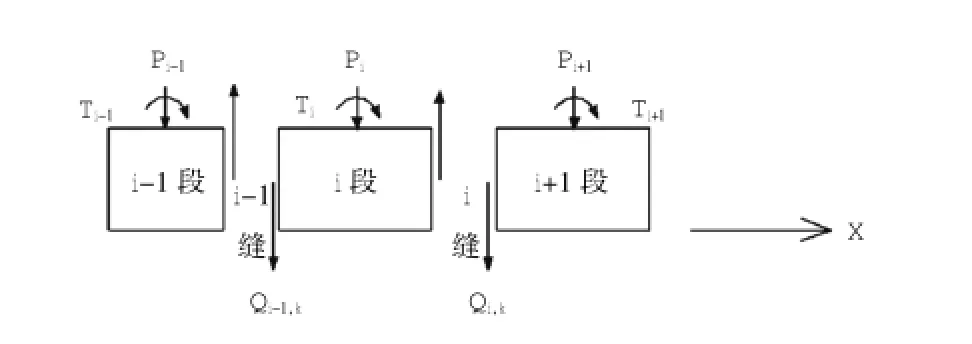
图2 并列铰接悬臂梁法计算图式Fig.2 Computing graph of parallel hinged cantilever method

由i截面位移协调条件可得控制方程[8]为

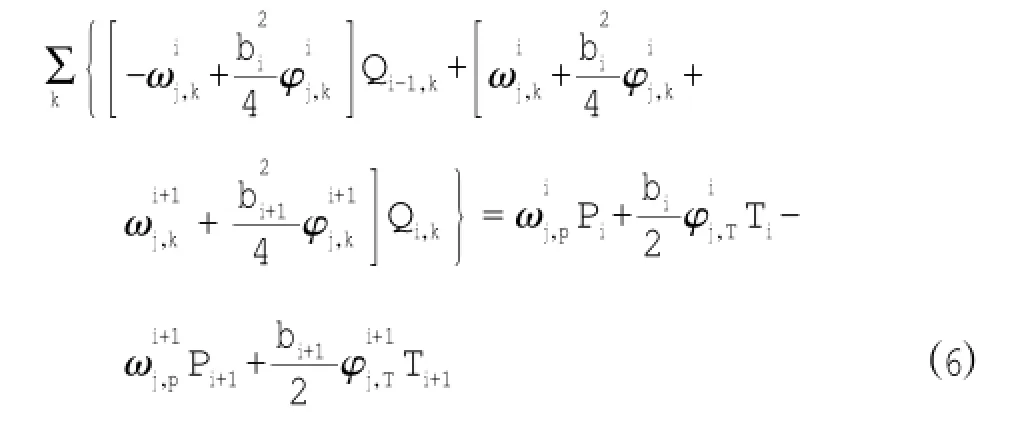
式中：Pi，Ti为作用在第i根梁上的横向合力及其产生的扭矩；为第i根梁k结点处，或横向合力点处作用单位力时，分别在j结点处产生的挠度；为第i梁根k结点处，或横向合力点处作用单位扭矩时，分别在j结点处产生的扭转角。

为了简化计算，取n=2，分别在横向荷载合力点高程、边墩顶部设置铰接点。

2 闸首横向不平衡剪力

闸首左右承受对称荷载时，横向合力自然等于0，在分段面上不会产生横向不平衡剪力。如果闸首横向荷载不对称时，应该研究横向不平衡剪力对底板内力的影响。

2.1 横向整体平衡分析

如图3所示，横向（y轴）荷载P作用下，在闸首基底形成横向剪力Q，产生的基底摩阻剪应力[7]τP。

式中：τP为基底摩阻应力，Pa；P为闸首横向荷载合力，N；Ix为基底面惯性矩，m4；Sy为基底面横向坐标y外侧静矩，m3；B为闸首长度，m；L为闸首宽度，相当于地基梁长度，m。

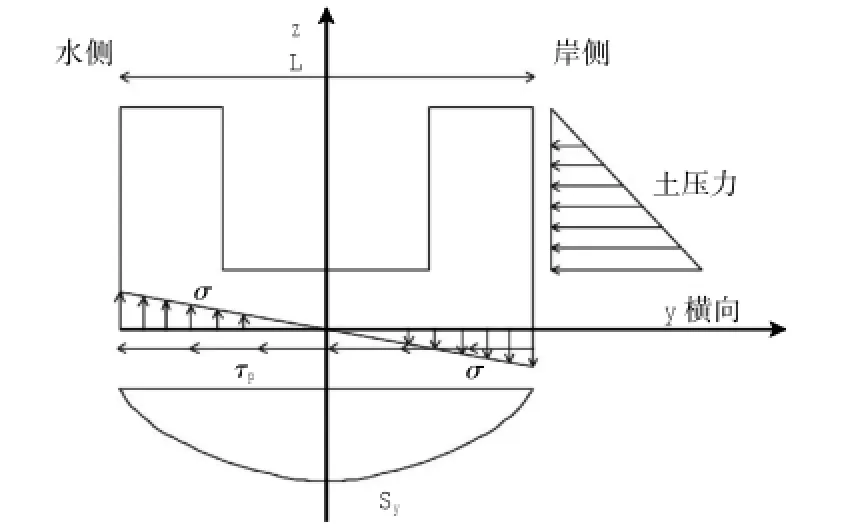
图3 横向不对称荷载受力简图Fig.3 Lateral asymmetric load stress diagram

2.2 横向不平衡剪力Qi

闸首在整体工作时横向荷载P、摩阻力τP是平衡的，而分段后特征段各自的横向力是不平衡的，因此分断面上必然产生横向剪力以使各段保持平衡。

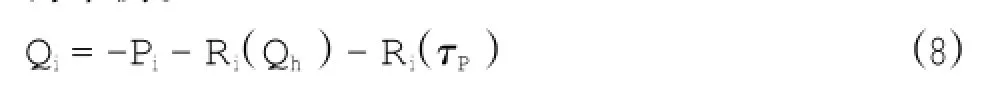
式中：Qi为第i特征段横向不平衡剪力，N；Pi为该特征段上横向荷载总和，N；Ri（Qh）为边墩横向荷载分配时分段截面传递的横向剪力，N；Ri（τP）为基底摩阻力在该特征段的合力，N。

2.3 不平衡剪力Qi分配

求得不平衡剪力Qi（合力）后，按材料力学公式计算在边墩、底板上的剪应力τQ1，τQ2，然后再分别积分得在边墩、底板上分配的不平衡剪力Qi1，Qi2。不平衡剪力Qi分配[9]的计算简图如图4所示，其中Qi1以集中力方式作用在边墩的H/2处，Qi2以均布力方式分配在口门宽度2L2内。

图4 横向不平衡剪力分配示意图Fig.4 Distribution diagram of lateral unbalance shear force

式中：Qi1，Qi2分别为在边墩、底板上分配的剪力，N；τQ1，τQ2为不平衡剪力Qi在边墩、底板上的剪应力，Pa；Iz为闸首分段面对竖轴z的惯性矩。

式（9）~式（11）可以验证满足条件

边墩、底板上剪力的分配系数m，n分别为

3 实例分析

3.1 工程概况

某船闸工程下闸首结构纵向长27.8 m，口门宽23.0 m，边墩宽8.8 m，横向总宽为40.6 m，高度17.4 m，为对称整体式结构，边墩顶高程48.6 m，底板底高程31.2 m、顶高程34.4 m、底板厚度3.2 m。由于船闸与水电站并列式布置，下闸首右侧为岸，回填土料，上游填土高度48.6 m，沿闸首纵向下降至下游34.4 m；左侧与水电站相接，无回填土。该闸首受力为非对称，且横向水、土压力沿纵向变化。

混凝土采用C25混凝土，E=3.0×104MPa，μ= 0.167。下闸首主要持力层为砂岩地基，压缩模量Es=29 MPa，泊松比μs=0.25。墙后回填土采用细砂，水上重度γ=17.58 kN/m3，摩擦角φ=30°，黏聚力C=0 kPa。为更好说明问题，本文只进行横向土压力作用下底板内力的计算，以有限元分析结果为精确值，对比分析横向荷载分配、整体扭转效应对计算结果的影响。

下闸首的结构有限元模型见图5所示，地基范围取底板以下厚度110 m，边墩外侧宽度140 m，上、下游面外侧宽度84 m，地基外边界均设置侧向约束。底板与地基之间设置接触面，分别采用contact170、contact173单元模拟。混凝土与地基采用solid45单元模拟[10]。

图5 下闸首ANSYS模型图（显示1/2）Fig.5 ANSYS model diagram of lower lock head（shows 1/2）

3.2 横向荷载分配结果及分析

根据规范的分段原则[2]，将闸首底板分为两段，其中门前段16.7 m、支持段11.1 m。在分段面处回填土高程40.0 m，门前段平均填土高程44.3 m，在底板顶高程以上填土高度9.9 m。各方法进行门前段横向荷载分配的结果见表2所示。

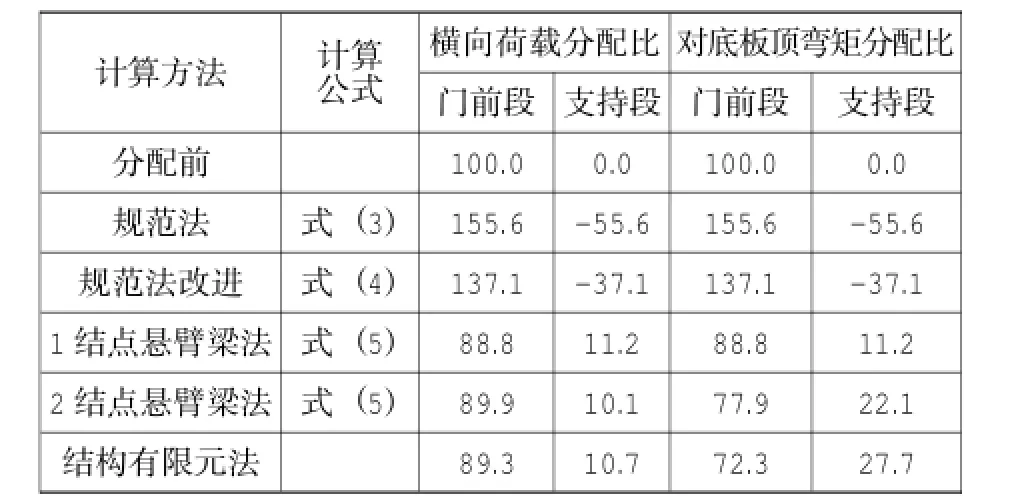
表2 横向荷载分配结果比较Table 2 Result comparison of lateral load distribution %

根据表1结果可知：1）由于扭转项在式（3）、式（4）中比例占优，Δb出现负值，规范法及其改进法分配到支持段横向荷载分别为-55.6%、-37.1%，结果显然是不合理的；2）在填土高度1/3处设1个结点的悬臂梁法，在两段的荷载分配比为88.8%、11.2%，与有限元结果89.3%、10.7%较为接近，但弯矩分配比仍有较大误差；3）在边墩顶部增设1个结点后，横向荷载、弯矩分配比不再相同，两者结果均与有限元结果十分接近，说明2结点悬臂梁法有较好的计算精度。

3.3 不平衡剪力Qi的计算及分配

由式（7）求得τP-max=6.77 kPa。由式（8）可求得门前段、支持段的不平衡剪力Qi，再由式（13）求得m=0.29，n=0.71，对Qi进行分配，其结果如表3。

表3 不平衡剪力计算分配表Table 3 Calculations and allocation of unbalance shear force kN

3.4 底板内力计算

3.4.1 计算情况

按照规范法及其改进法无法进行横向荷载分配，利用本文提出的横向荷载分配方法、整体剪切扭转分配方法分别确定各特征段荷载，利用郭氏法计算底板内力，结合是否进行内力调整，分析比较了以下6种计算结果，其中方法2、方法3是规范推荐的计算方法。

方法1：横向荷载不分配、底板内力计算；

方法2：横向荷载不分配、底板内力计算、内力调整；

方法3：横向荷载分配、底板内力计算；

方法4：横向荷载分配、底板内力计算、内力调整；

方法5：横向荷载分配、横向不平衡剪力、底板内力计算；

方法6：横向荷载分配、横向不平衡剪力、底板内力计算、内力调整。

内力调整时，考虑底板刚度的影响

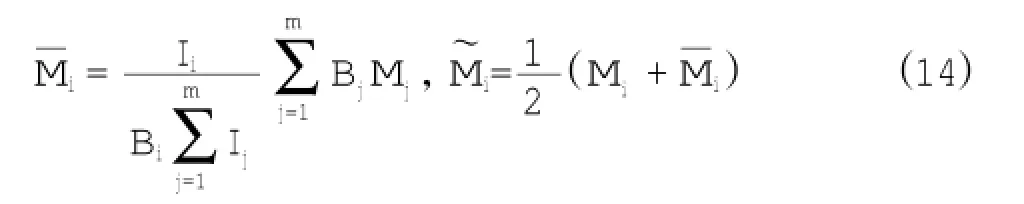
式中，Mi为第i特征段分段计算的单宽弯矩；Bj为特征段宽度；Ij为特征段抗弯惯性矩；Mi为按底板刚度分配的加权单宽弯矩，当底板等高时，等同于宽度权单宽弯矩；M˜i为调整后单宽弯矩。

3.4.2 计算荷载、计算参数

各种计算情况时，对底板中性轴力矩值见汇总表4。

表4 底板计算荷载表Table 4 Calculated load of bottom plate

郭氏法柔度系数[11]t=2.47，横向力对底板的弯矩作用在边墩中间位置更加合理[12]，门前段α1= 0.81、支持段α1=0.78。实际根据t=2，α=0.8查表计算内力。

3.4.3 结果分析

由横向荷载对基底倾覆力矩产生的地基反力，假设呈线性分布，可求得最大最小地基反力为±4.26 kPa，与有限元结果规律一致、结果接近，如图6所示。

图6 地基反力横向分布比较Fig.6 Comparison of lateral distribution subgrade reaction

6种方法与ANSYS有限元计算结果比较，见图7所示。为了全面比较各种方法的优劣，计算与有限元法结果的方差平均值σ，如表5所示。

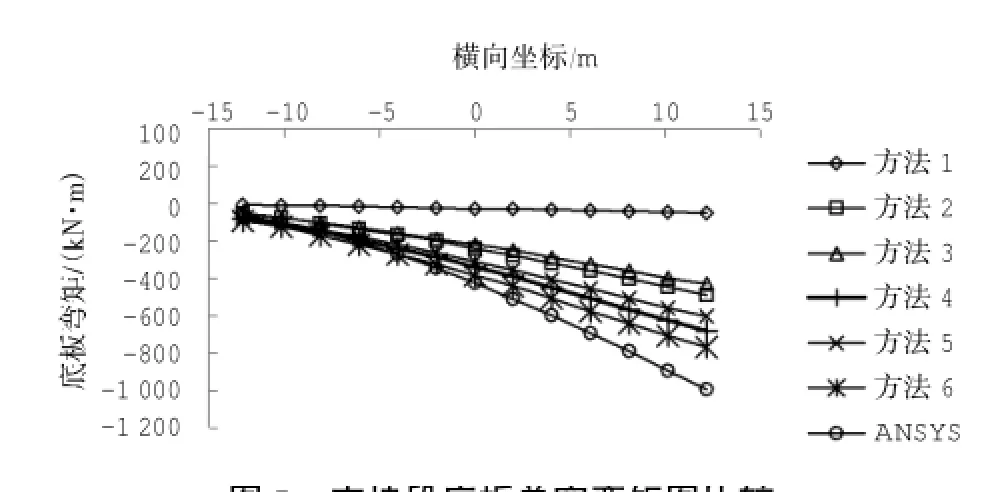
图7 支持段底板单宽弯矩图比较Fig.7 Comparison of bending moment diagram per unit width of bottom plate in the support section

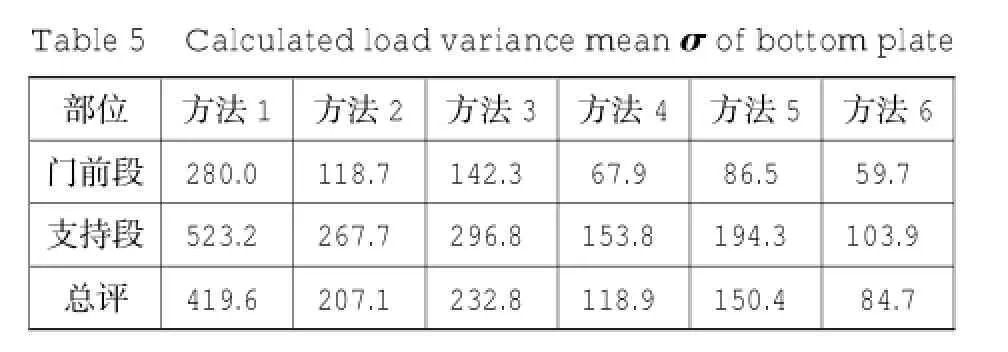
表5 底板计算荷载方差平均值σ

1）边墩横向荷载不分配直接进行分段内力计算，导致支持段内力严重偏小（方法1）。内力调整后内力偏差减小，计算精度提高（方法2）。

2）横向荷载预先分配使得边墩底与底板顶截面处受力更接近实际情况，相对分段底板而言，就是更好地模拟了边墩传递的荷载作用，因此，横向荷载分配使得底板内力计算精度更高（方法3与方法1对比）。

3）横向荷载分配仅仅是反映了边墩的整体作用，没有反映分段底板之间的整体作用。分段法通过考虑竖向不平衡剪力反映各特征段之间的相互作用，满足了静力平衡条件，但没有满足分段面之间位移协调条件，因此无论横向荷载是否先行分配，底板的内力均应进行分配调整（方法2、4、6分别与方法1、3、5比较）。

4）方法5、6分别与方法3、4比较表明，闸首两侧横向荷载不对称时，考虑横向不平衡剪力可以进一步提高计算精度。

5）综上所述，规范推荐的方法2（横向荷载不分配、内力进行调整）、方法3（横向荷载分配、内力不调整）计算结果接近，但方法4（同时进行横向荷载分配和内力调整）的计算精度更高。当横向荷载不平衡时，还应在方法4的基础上考虑横向不平衡剪力的影响（方法6）。

4 结语

1）规范推荐的基于侧向弯曲扭转变形的横向荷载分配方法仅适用于高水头船闸。本文提出的2结点并列悬臂梁法，能够考虑边墩高度的影响，反映了横向荷载、弯矩分配比不同的特征，两者结果均与有限元结果十分接近，有较好的计算精度。

2）分段法通过考虑不平衡剪力反映各特征段之间的相互作用（竖向、横向），满足了静力平衡条件，但没有满足分段面之间位移协调条件，因此无论横向荷载是否先行分配，底板的内力调整还是必要的。

3）横向荷载分配分别反映了两侧边墩的整体作用，仅考虑了边墩传至底板的荷载分布，对于承受横向不对称荷载的闸首，还应进行各特征段的横向相互作用分析。本文给出的横向不平衡剪力计算和分配方法合理，可以进一步提高内力计算精度。

[1]何良德，李岗.船闸闸首底板计算方法探讨[J].水运工程，1997（12）：30-34. HE Liang-de，LI Gang.Lock gatefloor calculation method[J].Port &Waterway Engineering，1997（12）：30-34.

[2]刘晓平，陶桂兰.渠化工程[M].北京：人民交通出版社，2009. LIU Xiao-ping，TAO Gui-lan.Drainage engineering[M].Beijing：China Communications Press，2009.

[3]JTJ 307—2001，船闸水工建筑物设计规范[S]. JTJ 307—2001，Code for design of hydroalic structures of shiplocks [S].

[4]刘秀魁.闸首底板不对称荷载作用下的内力计算分析[D].南京：河海大学，2010. LIU Xiu-kui.The analysis of gatefloor internal force under asymmetric loads[D].Nanjing：Hohai University，2010.

[5]苏兴海.不对称荷载作用下的闸首底板计算方法研究[D].南京：河海大学，2013. SU Xing-hai.The analysis of the stress and strain in the bottom plate of the lock head by the asymmetric load[D].Nanjing：Hohai University，2013.

[6]陈国荣.弹性力学[M].南京：河海大学出版社，2009. CHEN Guo-rong.Elasticity[M].Nanjing：Hohai University Press，2009.

[7]徐道远，黄孟生.材料力学[M].南京：河海大学出版社，2002 XU Dao-yuan，Huang Meng-sheng.Mechanics of materials[M]. Nanjing：Hohai University Press，2002.

[8]何良德，梅霆，周俊波，等.基于分层地基模型的闸首分缝底板计算方法[J].河海大学学报（自然科学版），2012，40（6）：698-703.

HE Liang-de，MEI Ting，ZHOU Jun-bo，et al.Calculation method of parting floor of lock head based on layered foundation model[J]. Journal of Hohai University：Natural Sciences，2012，40（6）：698-703.

[9] 王宝明.不平衡剪力分配系数积分计算方法[J].东北水利水电，1997（2）：15-16. WANG Bao-ming.Imbalance shear distribution coefficient integral calculation method[J].Water Resources&Hydropower of Northeast China，1997（2）：15-16.

[10]王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007. WANG Xin-min.Numerical analysis of ANSYS engineering structure[M].Beijing：China Communications Press，2007.

[11]龙驭球.弹性地基梁的计算[M].北京：高等教育出版社，1981. LONG Yu-qiu.Calculation of the beam on elastic foundation[M]. Beijing：Higher Educations Press，1981.

[12]苏超，阚得静.葛氏法计算船闸坞式结构底板时荷载简化方式研究[J].水运工程，2012（4）：134-138. SU Chao，KAN De-jing.Simplified method of calculating load acted on dock floor of ship lock using Ge′s method[J].Port&Waterway Engineering，2012（4）：134-138.

Allocation method about lateral load and unbalance shear force of the lock head

HE Liang-de1，2，LIU Jiang-lin2，HE Ying-fa2，XU Ke2
（1.Key Laboratory of Coastal Disaster and Defence，Ministry of Education，Hohai University，Nanjing，Jiangsu 210098，China；2.College of Harbor，Coastal and Offshore Engineering，Hohai University，Nanjing，Jiangsu 210098，China）

In order to improve the accuracy and extend the application scope of gate floor longitudinal segmentation method，as the lateral load allocation method of code for ship locks is inadequate，this paper analyzes the transfer mechanism of lateral load on side piers，proposes parallel articulated cantilever method，and for the first time to conduct the analysis of lateral overall balance，then provides allocation method of lateral imbalance shear force.The calculation of engineering example shows that the internal force adjustment after lateral load allocation is necessary.The two node parallel cantilever method is able to consider the impact of side piers height，also reflects the different characteristics of lateral load and bending moment distribution ratio.For the lock head withstands lateral asymmetric load，lateral imbalanced shear calculation and allocation is also necessary.The comparative analysis with finite element results shows that after lateral load allocation，unbalanced lateral shear force allocation，internal force adjustment，the result of bottom plate internal force is highly accurate.

waterway engineering；lock；parallel cantilever method；lateral load allocation；lateral unbalance shear；internal force adjustment

U641.31

：A

：1003-3688（2014）03-0037-06

10.7640/zggwjs201403007

2013-08-31

2013-12-24

何良德（1964— ），男，上海市人，副教授，硕士生导师，主要从事港口与航道工程结构研究。E-mail：hldhsy@163.com