基于Chan-Vese模型的TFT-LCD Mura缺陷快速分割算法
2014-03-21卢小鹏刘云杰
卢小鹏,李 辉*,刘云杰,梁 平,李 坤
(1.电子科技大学 航空航天学院,四川 成都611731;2.四川出入境检验检疫局 机电处,四川 成都610041)
1 引 言
随着液晶显示器向大尺寸、轻薄化、低功耗、高分辨率的方向发展,TFT-LCD 在生产过程中产生各种显示不均匀缺陷的几率大大增加。亮点、亮线、暗线等缺陷由于其特征明显,易于检测。而Mura缺陷对比度低,边缘模糊,大小、形状都不固定,而且背景图像复杂,这就增加了缺陷分割的难度,成为研究的热点[1-2],并且传统的图像分割方法无法得到满意的分割效果。
Osher等人[3]于1988年提出了计算稳定、抗噪性好且具有跟踪拓扑结构变化的水平集方法,并成功运用到图像处理中。Caselles[4]和Malladi[5]等人以曲线演化理论和水平集方法为基础,分别独立地提出了几何主动轮廓模型,将图像分割问题转化为求能量泛函的最优解问题。而后,Caselles等人又对几何主动轮廓模型做了改进,提出了测地主动轮廓模型[6]。国内的周则明等[7]利用Snake 模型并结合水平集方法对左心室MRI图像进行分割。但以上方法都存在基于图像梯度的边缘检测项,只能检测用梯度定义的图像边 缘。2001 年,Chan 和Vese 简 化 了Mumford-Shah[8]模 型,并 结 合 水 平 集 思 想,提 出 了Chan-Vese水 平 集 模 型[9],即 经 典 的C-V 模 型。C-V 模型不再依赖图像的梯度信息,适用于梯度无意义或者边缘模糊的图像的分割。但是,C-V模型以2个灰度均值拟合描述目标和背景2个同质区域,对于背景不均匀的图像无法准确地分割。同时,每次的更新迭代,都要重新初始化符号距离函数,计算量大,降低了目标检测效率。
在数值实现上,常用的求解格式有有限差分格式、AOS[10]格式等。有限差分格式必须在较小的时间步长下才能得到稳定解,计算效率低;而AOS格式虽然可以采用较大的时间步长,但在迭代过程中需要多次计算矩阵的逆而使得分割精度下降。本文针对C-V 模型,在模型本身、数值实现等方面加以改进,提高了模型对背景不均匀图像的分割能力和分割速度。
2 传统的C-V 模型
假设定义域为Ω 的图像I(x,y)被闭合曲线C 划分为目标、边界2个区域Co、Cb,其平均灰度分别为co、cb。C-V 模型在实现过程中,需要把演化曲线C 嵌入到水平集函数φ 中,同时引入Heaviside函数和Dirac函数,则C-V 模型的水平集表示为:
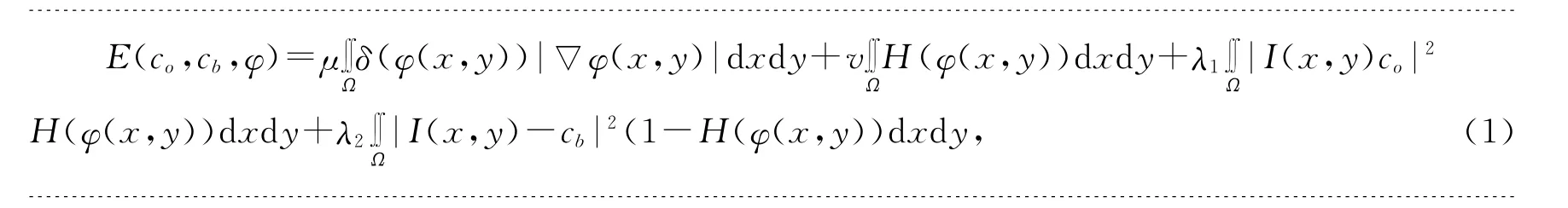
其中:μ≥0,v≥0,λ1>0,λ2>0为常数。
Chan和Vese以欧拉—拉格朗日方法求解式(1),并利用梯度下降流得到最终的偏微分方程:
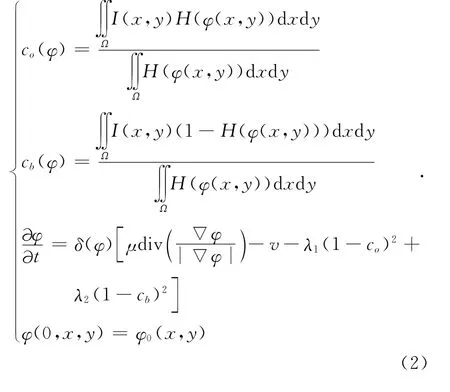
传统的C-V 模型主要根据区域的灰度均值特性处理背景简单的两类分割问题,而对于背景复杂的图像无法准确地分割。另外,水平集函数φ 必须构造为符号距离函数,φ 经过少量的迭代演化后,就会背离符号距离函数,通常以重新初始化符号距离函数来保持计算的稳定性,这样致使计算量增大和演化速度降低,同时分割的准确度也受到影响。
3 改进的C-V 模型
为了解决符号距离函数重初始化问题,Li[11]等人在建立基于梯度的参数活动轮廓模型时,根据符号距离函数的梯度始终满足|φ|=1,在能量函数中增加一惩罚项:
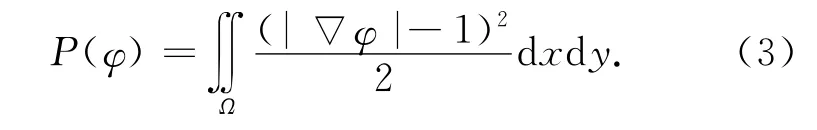
对于任何偏离|φ|=1的局部,在后续演化过程中将被纠正,因此,无需重新初始化符号距离函数。
为了平衡图像背景整体亮度不均匀对检测效果的影响,在传统的C-V 模型中增加一个与轮廓曲线内、外部区域之间的亮度差有关的能量项,该能量项可以描述为:
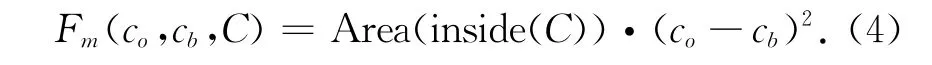
这里,Area(inside(C))是曲线内部的面积。
综上所述,改进后的C-V 模型为:
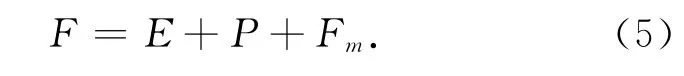
整理可得改进模型的能量方程为:
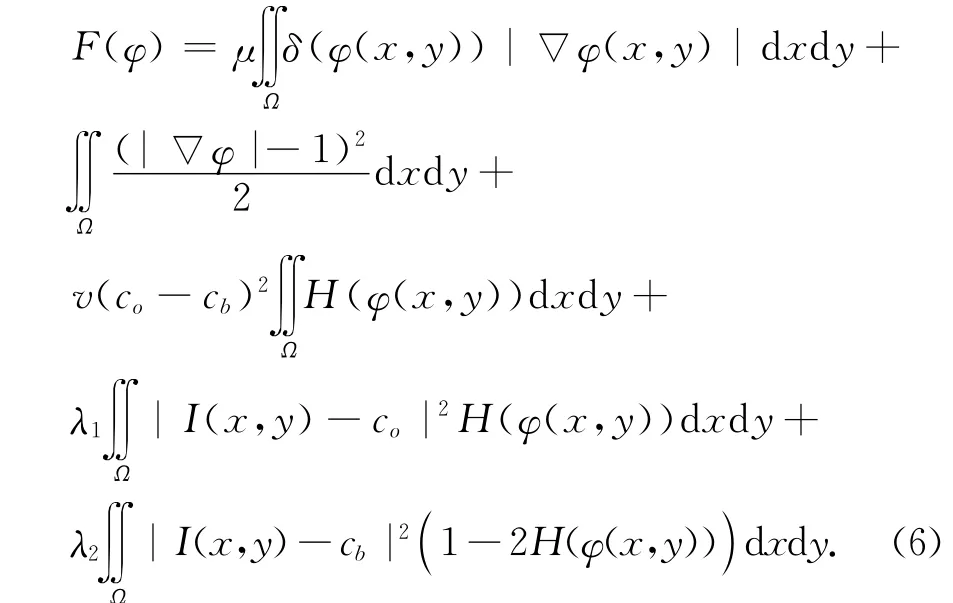
式(6)对应的演化方程如下:
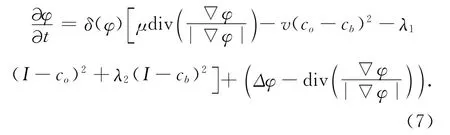
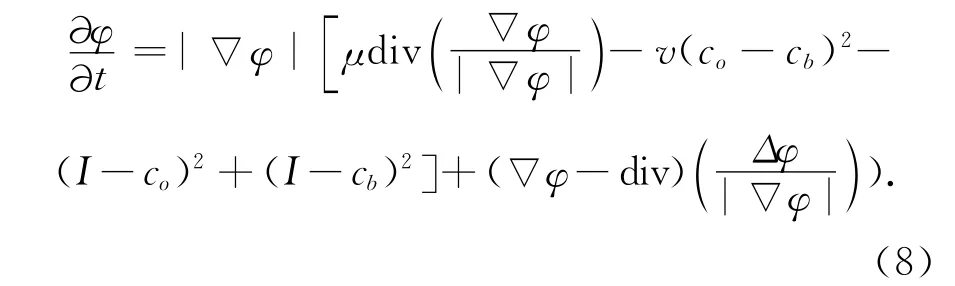
对于长度参数μ,当检测较大的物体时,应取较大值,反之亦然。通过修改参数v的值,可以平衡图像整体的亮度不均匀。
4 数值实现
4.1 半隐差分格式构造
对于式(8)模型的离散化过程通常采用有限差分格式或AOS 格式。半隐差分格式与AOS格式一样都是无条件稳定的,但其在一次迭代过程中有选择地不更新一些函数项的前次迭代结果,使得每次迭代步中都包含最近两次的迭代数据。
设时间步长为τ,空域步长为h,则对于式(8)中各项,首先构造如文献[12]中的半隐差分格式。记
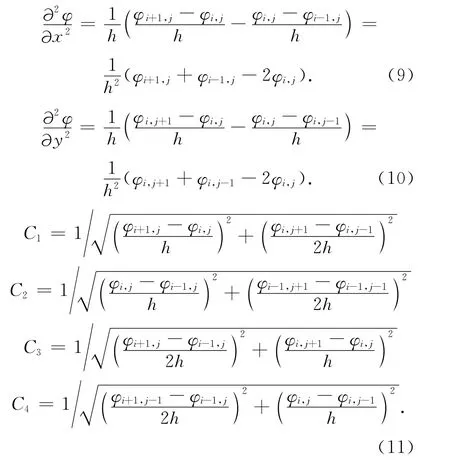
则曲率的差分格式为:
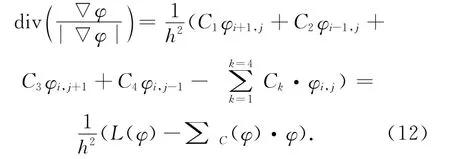
其中:
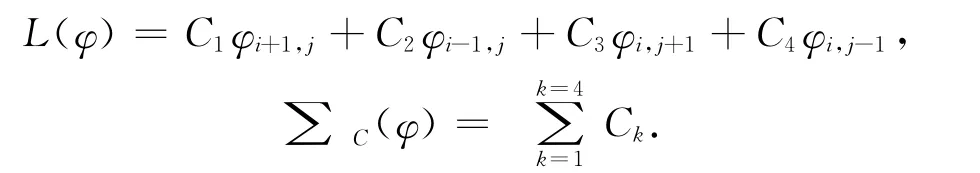
同时,水平集函数的Laplace算子为:
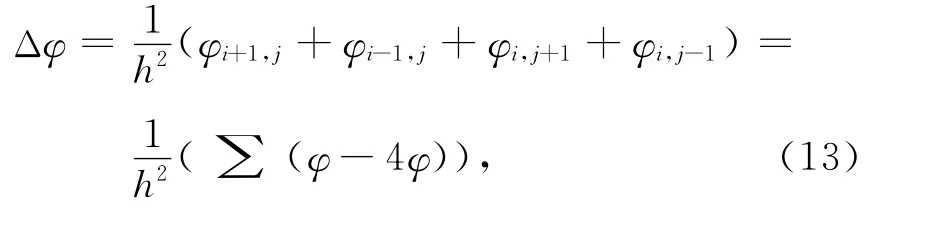
其中:
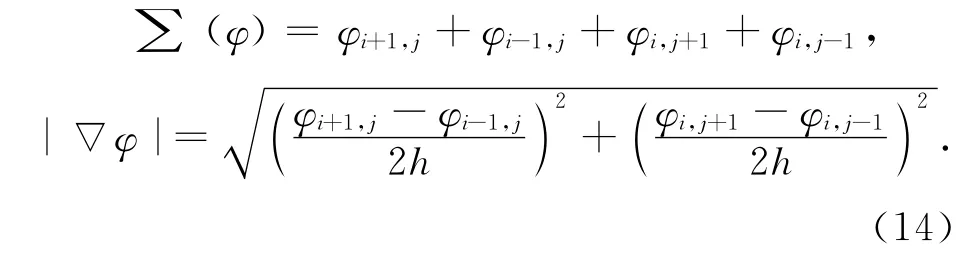
另外,记
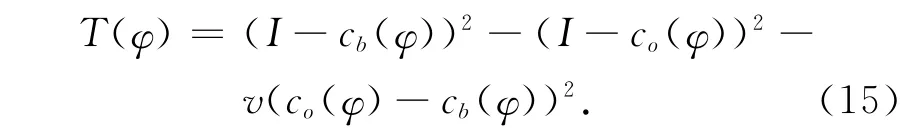
这里,
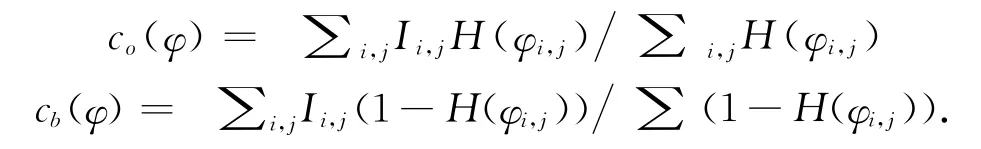
则式(8)的离散迭代式为:
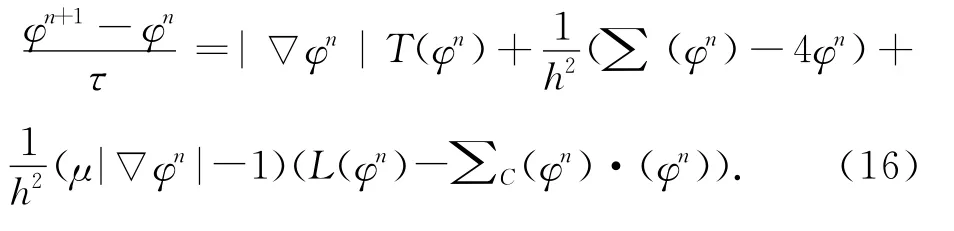
由此可得其半隐差分格式为:
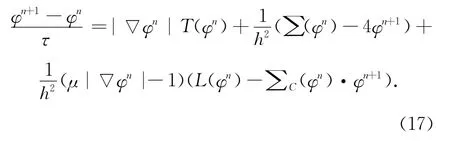
整理式(17)可得形如文献[12]中出现的数值模型:
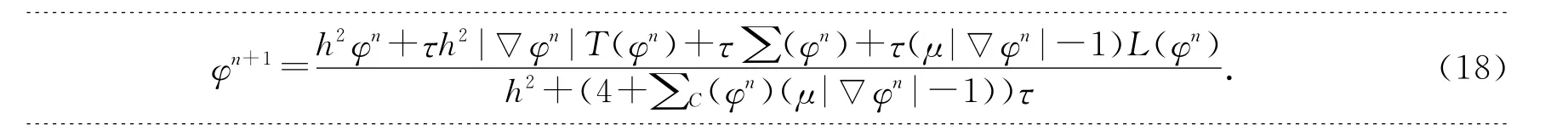
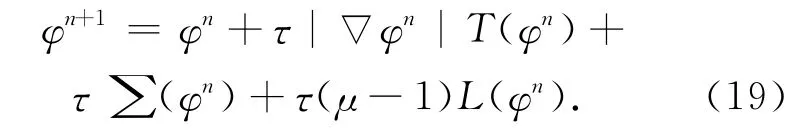
4.2 迭代停止控制
半隐差分格式是无条件稳定的,并且演化速度快,容易出现过收敛现象。为了准确分割目标,谢强军等人[13]采用了曲线演化的自动停止判定不等式

5 实验结果分析
实验硬件环境为Intel(R)Core(TM)i3CPU 530@2.93GHz,4.00GB内存;软件环境为:MatlabR2010a。实验参数设定为:μ=0.000 1×2552。
首先说明符号距离保持项P(φ)对模型的作用。对一副270×220的合成图像,分别用去掉项的改进模型和完整的改进模型进行分割,结果如图1所示。去掉P(φ)项,模型在每次迭代过程中需要重新初始化符号距离函数,虽然迭代次数不变,但会影响到分割速度。由于迭代次数NumIter=3,去掉P(φ)项的改进模型的计算时间Cputime也只有0.82 989s,但完整的改进模型的计算时间减少了22.6%。随着图片尺寸增大和迭代次数增加,重初始化距离符号函数将会严重影响模型的分割速度。

图1 去掉项的改进模型和完整的改进模型的分割效果比较Fig.1 Comparison of segmentation results between improved model without and improved model
图2分别用传统的C-V 模型和改进后的CV 模型分别对一副的TFT-LCD 线Mura缺陷图像和一副的TFT-LCD 块状Mura缺陷图像进行分割,亮度不均平衡系数分别取v=4.7 和v=1.9。可以看出,传统的C-V 模型无法对背景不均匀的Mura缺陷图像准确分割,而改进后的CV 模型得到了满意的分割效果。

图2 传统的C-V 模型和改进后的C-V 模型缺陷分割效果比较Fig.2 Comparison of segmentation results between traditional C-V model and improved C-V model
为了验证半隐差分求解格式的高效性,对一副450×400 的TFT-LCD 块状Mura缺陷图像分别用有限差分格式、AOS格式和半隐差分格式进行检测,结果比较如表1所示。
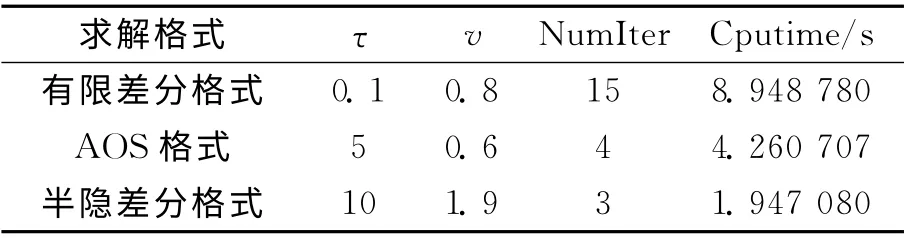
表1 半隐差分格式与有限差分格式、AOS格式的求解效率比较Tab.1 Comparison of solving efficiency among finite difference scheme, AOS and semi-implicit scheme
3种求解格式都能实现对Mura缺陷的准确分割,从表1可以看出,有限差分格式必须在较小的时间步长下才能得到稳定解,曲线演化缓慢;而AOS格式虽然加大了时间步长,但迭代过程中需要多次求解矩阵的逆,计算量增加;半隐差分格式无需进行矩阵求逆运算,而且时间步长可以达到τ=10,计算效率明显提高。
6 结 论
本文主要针对传统的C-V 模型对背景复杂的图像分割不准确,并且耗时长的缺点,通过改进模型本身和求解格式,提高了模型分割图像的准确度和分割速度。实验结果表明,改进的C-V 模型提高了对背景复杂的图像的分割能力。在数值实现上,半隐差分格式克服了有限差分格式步长较小,AOS格式矩阵求逆的不足,进一步增大了时间步长,而且分割速度更快。本文提出的算法对背景不均匀图像有很好的分割效果,能够实现对TFT-LCD Mura缺陷的快速检测。
[1] 周哲.横线Mura的分析与改善[J].液晶与显示,2012,27(5):649-652.Zhou Z.Analysis and improvement of horizontal line Mura[J].Chinese Journal of Liquid Crystals and Displays,2012,27(5):649-652.(in Chinese)
[2] 齐鹏,施园,刘子源.TFT-LCD Touch Mura不良的研究和改善[J].液晶与显示,2013,28(2):204-209.Qi P,Shi Y,Liu Z Y.Research and improvement of touch Mura in TFT-LCD [J].Chinese Journal of Liquid Crystals and Displays,2013,28(2):204-209.(in Chinese)
[3] Osher S,Sethian J A.Fronts propagating with curvature dependent speed:Algorithms based on the Hamilton-Jacobi formulation[J].Journal of Computational Physics,1998,79(1):12-49.
[4] Caselles V,Catte F,Coll T,et al.A geometric model for active contours in image processing[J].Numerische Mathematik,1993,66(1):1-31.
[5] Malladi R,Sethian J A,Vemuri B C.Shape modeling with front propagation:A level set approach[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1995,17(2):158-175.
[6] Caselles V,Kimmel R,Sapiro G.Geodesic active contours[J].International Journal of Computer Vision,1997,22(1):61-79.
[7] 周则明,尤建洁,范春晖,等.结合水平集方法和形状约束Snake模型的左心室MRI图像分割[J].模式识别与人工智能,2006,19(6):782-786.Zhou Z M,You J J,Fan C H,et al.Left ventricle MRI images segmentation by unifying level set method and snaked model with shape constraints[J].Pattern Recognition and Artificial Intelligence,2006,19(6):782-786.(in Chinese)
[8] Mumford D,Shah J.Optimal approximations by piecewise smooth functions and associated variational problems[J].Communication on Pure and Applied Mathematics,1989,42(5):577-685.
[9] Chan T F,Vese L A.Active contours without edges[J].IEEE Transactions on Image Processing,2001,10(2):266-277.
[10] Kuhne G,Weickert J,Beier M,et al.Fast implicit active contour models[C].Proceedings of the 24th DAGM Symposium on Pattern Recognition,Germany:springer-verlag,2002:133-140.
[11] Li C,Xu C,Gui C,et al.Level set evolution without re-initialization:A new variational formulation[C].Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.San Diego,USA:IEEE Computer Society,2005:430-436.
[12] Chan T F,VESE L A.A multiphase level set framework for image segmentation using the Mumford and Shah model[J].International Journal of Computer Vision,2002,50(3):271-293.
[13] 谢强军,侯迪波,黄平捷,等.一种改进的单参数水平集快速分割方法[J].光电子·激光,2009,20(12):1671-1675.Xie Q J,Hou D B,Huang P J,et al.An improved level set method for fast image segmentation based on dingle parameter[J].Journal of Optoelectronics·Laser,2009,20(12):1671-1675.(in Chinese)
