基于小波去噪结合CVA-ICA的故障检测方法的研究
2014-03-21杨英华李智辉
李 召,杨英华,李智辉
(1.许继电源有限公司,河南许昌 461000; 2.东北大学信息科学与工程学院,辽宁沈阳 110819)
0 引言
随着现代经济的快速发展和流程工业规模的不断扩大,工业过程的复杂性也不断提高,这类系统一旦发生故障,将会造成不可估量的损失。因此,在生产过程中进行故障诊断是必不可少的。当工业过程中存在互相关的情况时,主元分析(PCA)[1]和核主元分析(KPCA)[2]是效果比较理想的故障检测方法,但是在处理含有强自相关的工业过程时,这两种方法却显得力不从心。若考虑到大多数工业过程数据的非高斯性分布假设,PCA及KPCA方法中控制限求取的假设前提就不能成立,而独立成分分析(ICA)能从非高斯分布的数据中提取出独立源,因此在故障检测方面有更广泛的应用价值[3-4]。然而,当工业过程为动态时,ICA方法的故障检测效果也不是很明显。规范变量分析(CVA)是一种动态的线性降维方法[5],最初用于多变量统计分析中,它也可以处理含有自相关的情况,国内对CVA的研究还处于初步阶段,在故障检测方面的应用还非常少。
事实上,前面介绍的这些方法应用到过程监测当中时都没有考虑到噪声环境的影响。现场数据中不可避免地包含了不同程度地明显误差、测量噪声和系统噪声,噪声水平将直接影响到最终模型的准确性。针对这种情况,文中考虑在CVA和ICA算法之前首先利用小波去噪对数据进行预处理,然后再结合CVA和ICA进行故障检测。通过对 TE过程仿真结果对比,验证了该方法较其它方法具有更好的故障检测效果。
1 基本方法
1.1小波去噪原理
叠加性高斯噪声是最常见的噪声模型,一个受到叠加性高斯噪声污染的一维观测信号的模型可以表示成如下形式:
si=fi+σzi
(1)
式中:fi为代表真实信号;zi为噪声信号;σ为噪声标准差,即噪声强度,i=1,2,…,n,去噪的目标是从含噪数据si得到fi的一个最优逼近信号。
从信号处理的角度看,小波去噪实际上是特征提取和低通滤波的综合,其中特征提取就是将含噪信号进行多尺度小波变换,低通滤波可以看作是在多尺度下尽可能提取出信号的小波系数而过滤掉噪声的小波系数[6]。小波变换法去噪的一般过程为:首先对观测数据作小波分解,得到相应的小波分解系数;然后利用阈值等形式对小波分解系数进行处理,得出估计小波系数;最后对处理过的小波系数作逆变换重构信号,即可达到消除噪声的目的。
为了把小波去噪应用到工业过程的在线状态,文中在离线建模和在线监测时分别采用了Donoho和Johnstone[7]提出的非线性小波变换阈值法以及R.Bakshi[8]教授等提出的在线多尺度滤波算法(OLMS)去噪,其中OMLS的实现可以参考文献[9]。
1.2规范变量分析
CVA是一种动态的线性降维技术,在将2个变量间的相关度最大化方面是最优的。对于动态过程监控,CVA通过最大化历史数据集和未来数据集之间的相关度来得到过程的特征信息,从而建立过程的统计模型[10]。
假设一个非线性动态系统可简化为如下模型:
x(k+1)=Ax(k)+w(k)
y(k)=Cx(k)+e(k)
(2)
式中:矩阵A和C分别是状态矩阵和输出矩阵;w(k)和e(k)为模型误差且服从非高斯分布;x(k)和y(k)分别为k时刻的系统状态和输出。
为了更好地分析和解释动态系统,假设输出向量y(k)∈Rm,包含了m个输出的测量值。定义过去和未来的信息量yp(k)和yf(k),分别如下:
yp(k)=[y(k-1)y(k-2)…y(k-q)]T
(3)
yf(k)=[y(k)y(k+1)…y(k+q-1)]T
(4)
式中:q为延迟时间数,主要取决于系统的阶次。yp(k)和yf(k)包含了过去和未来q个时刻的输出向量信息。定义过去和未来的输出Hankel矩阵Yp和Yf分别为:
(5)
(6)
(7)
(8)
由式(8)可以得到输出样本数n和延迟时间q以及Hankel矩阵的列数N之间的关系:
N=n-2q+1
(9)
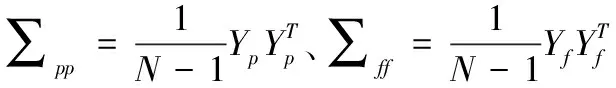
H=U∑VT
(10)
(11)
1.3独立分量分析
ICA方法是近几年才发展起来的一种新型统计方法,传统的ICA模型为:
x=As+e
(12)
式中:A∈Rm×n为未知混合矩阵;x为m维观测信号;s为n维源信号;e为误差矢量。
ICA的最终目的是寻找一个分离矩阵W,使得

(13)
能尽可能的逼近真实源信号s[11]。文中采用快速固定点ICA算法(算法详细描述参见文献[12])对式(11)中的规范变量进行分解,求取其独立元。
2 基于小波去噪结合CVA-ICA的故障检测策略
基于小波去噪结合CVA和ICA的故障检测策略在于观测数据矩阵首先进行了小波去噪预处理以达到了去噪、抗干扰的目的,然后对数据矩阵运用CVA处理解除变量之间的自相关和互相关性,最后对规范变量矩阵进行ICA处理,构建统计量I2检测系统是否发生故障。考虑到独立元信号并不服从高斯分布,因此,ICA方法一般采用非参数化的方法求取控制限,通常采用核密度估计(KDE)的方法构建过程的控制限。单变量核密度函数可表示为:
式中:K(.)表示核函数,常用的核函数有多项式核、高斯核、sigmoid核等,其选取可以参考文献[13],文中选取高斯核函数;h为平滑因子,可通过h≈1.06n-0.2δ来估算;δ为采样的标准差;zi是正常工况下监控统计量的采样点,i=1,2,…,n;n为采样个数。
为减少计算量,这里引入一种近似的方法来求取控制限的值。假设z′就是占据了98%区域的那一点,即存在:
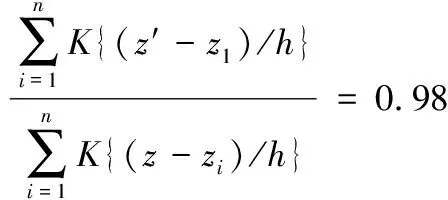
则能够很方便的求取统计量近似的控制限。
文中提出的基于小波去噪结合CVA-ICA的故障检测算法包括2个部分,分别是离线训练和在线监测,下面对它们的主要步骤作简单介绍。
2.1离线训练
离线训练的具体步骤如下:
(1)小波去噪预处理
从历史数据库中,选择正常工况下的观测变量数据。选择合适的基小波和分解层数,利用非线性小波变换软阈值去噪的方法对其进行预处理;
(2)构造Hankel矩阵并归一化
将步骤(1)得到的观测变量数据Y∈Rm×n(m为变量数,n为采样数)判断系统阶次,确定延迟时间,然后利用式(7)和式(8)构造过去和未来的输出Hankel矩阵。
文中应用Akaike信息判据(AIC)的方法确定延迟时间q,假定q∈(1,…,qmax),则q是使式子:
AICn(q)=n(my(1+ln2π)+ln|∑q|)+2δqMq

(3)利用式(10)和式(11)求取规范变量矩阵Z;
(4)对规范变量矩阵进行ICA处理,得到分解矩阵W和混合矩阵A;
(6)计算独立元和过去数据的估计量
(14)
(6)计算正常操作数据的I2,SPE监控统计量
(15)

2.2在线监测
在线监测的具体步骤如下:
(8)按照式(16)的形式构建在线采样向量,并利用在线多尺度滤波算法(OLMS)对其进行去噪预处理;
(16)
(10)根据式(17)计算在线采样下独立元信号和输出估计量:
(17)
(11)计算测试数据的监测统计量;
(12)判断监测统计量是否超限,若超限,则判定为工况异常或有故障发生,进行后续处理。
图1给出了小波去噪结合CVA-ICA的故障检测方法的流程。

图1 小波去噪结合CVA-ICA的故障检测流程图
3 仿真研究
田纳西-伊斯曼过程(TEP)[15]是Eastman化学公司创建的,其目的是为评价过程控制和监控方法提供一个现实的工业过程,工业流程如图2所示。目前,TEP已经作为典型的化工过程故障检测与诊断对象被广泛研究。整个过程包括5个主要的操作单元,即反应器、冷凝器、气液分离器、循环压缩机和产品解压塔,共有4个反应,生产2种产物,TEP包括12个控制变量和41个测量变量(包括22个连续测量变量和19个成分测量值),其中,反应器的搅拌速度为定值,故共有52个观察变量,所有的过程测量值都包含高斯噪声。
TE过程引入闭环控制的仿真程序可以仿真正常的工况和预设的21个故障,每次运行的仿真时间为48 h,采样间隔为3 min.在试验当中,选取500组正常工况下的数据进行训练建立过程的监测模型,选取每种故障下的480组异常工况数据进行测试,整个过程的训练和测试数据可以从网站http://brahms.scs.uiuc.edu下载。

图2 TE过程工艺流程图
仿真时,该算法的一些参数需要给定或者计算。通过MATLAB不断调试,小波去噪时选取db5正交小波为基小波,分解层数为5,采用基于启发式阈值形式的软阈值法;CVA处理时,由Akaike信息标准(AIC)确定TE过程的延迟时间数q=3;ICA中设定选取的独立元个数为8,在用FastICA求取分离矩阵中核函数选取径向基函数,I2,SPE统计量的控制限置信度为98%.
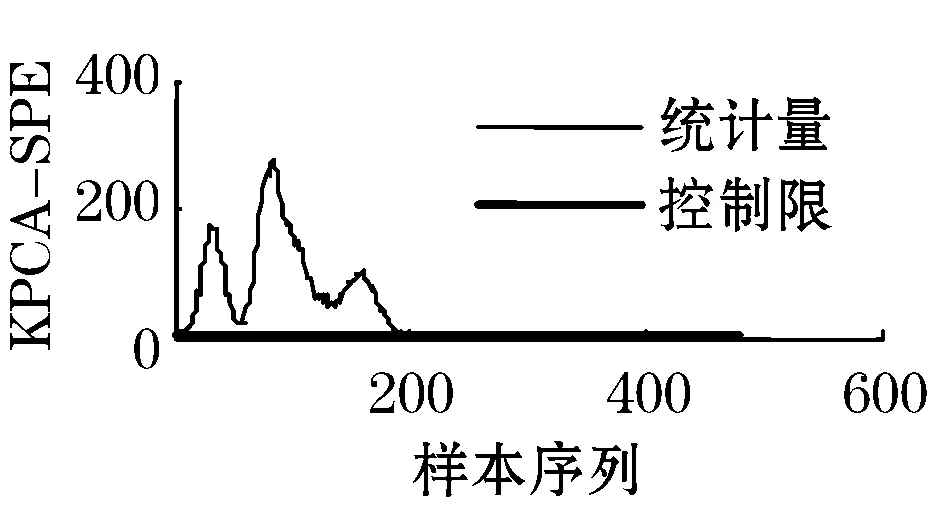
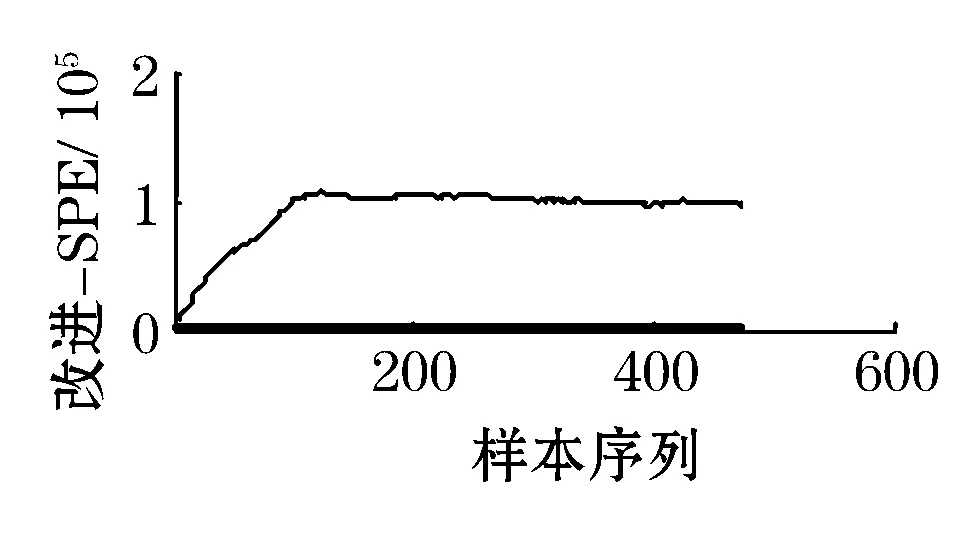
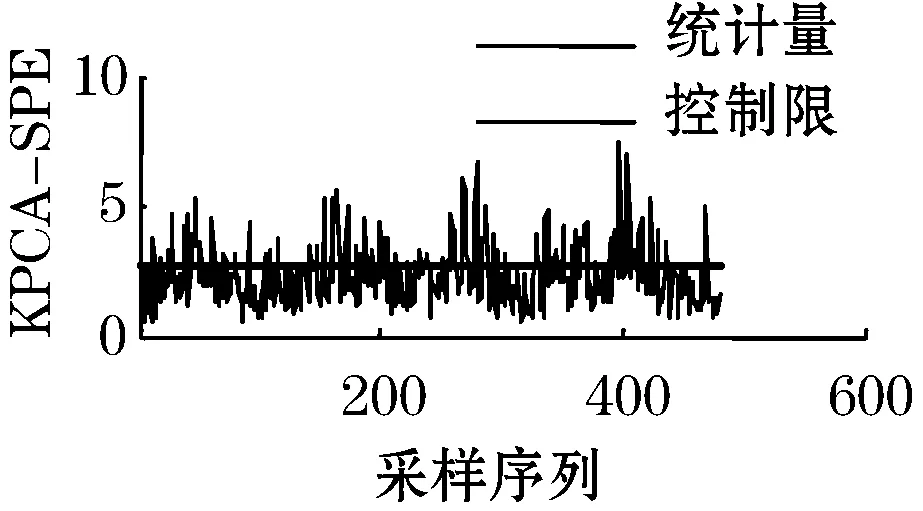
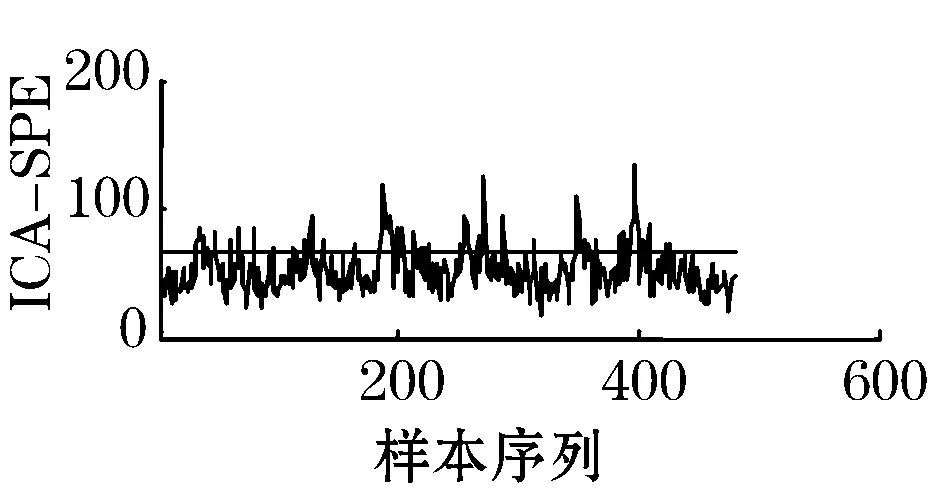
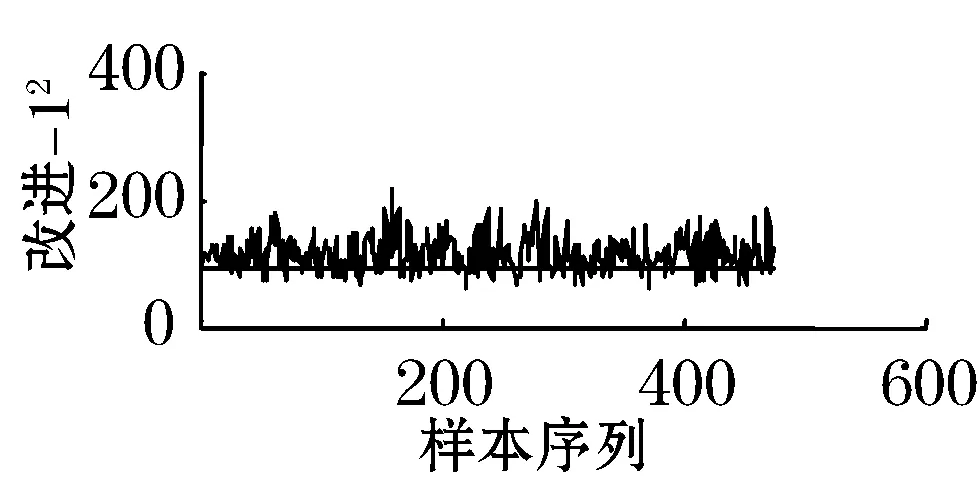
当故障5发生时,冷凝器冷却水的入口温度发生一个阶跃变化,图3是针对故障5分别运用KPCA、ICA和小波去噪结合CVA-ICA的方法得到的和对比图。
(a)

(b)

(c)

(d)
(e)

(f)
从图3中可以看出,KPCA方法的和统计量曲线在故障发生的一段时间内是位于控制限之上的,但是在一段时间后,大约是在第200个采样时刻,统计量曲线落在了控制限之下,这和实际过程发生故障不相符,表明KPCA方法无法很好的监控到此类故障的发生,出现这种情况的原因是在大约第200个采样开始,由于闭环控制的补偿作用,使其他变量恢复到正常值,导致统计量基本不超限。但是ICA和小波去噪结合CVA-ICA的方法克服了这个缺点,很好的检测到故障5的发生。
图4是3种方法对故障3的检测效果比较。这是一种比较难检测的故障,它是由D的进料温度(流2)阶跃变化造成。
从图示中可以看出KPCA和ICA两种方法几乎无法检测到故障3,另外,文献[16]中的DPCA,以及[17]中的DICA对它的检测效果也不理想,但小波去噪结合CVA-ICA方法的SPE、I2统计量曲线基本都超出了它们各自的控制限,这表明小波去噪结合CVA-ICA的方法可以较好的检测出故障3。
为了更好地说明小波去噪结合CVA-ICA的方法较其它方法的优越性,下面给出KPCA、ICA和小波去噪结合CVA-ICA的方法应用于TE过程故障检测时的SPE和T2/I2漏检率对照,如表1所示。
(a)

(b)
(c)

(d)

(e)
(f)
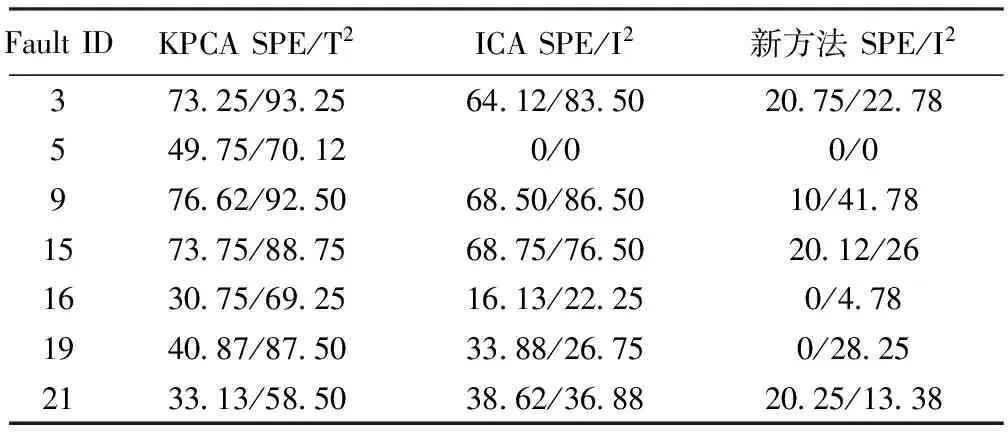
表1 故障漏检率比较(%)
表1中未列出漏检率的故障,表示三种方法对其检测效果都较好,由表1可以看出小波去噪结合CVA-ICA方法较KPCA和ICA对大多数故障的漏检率都较低,而且对诸如故障3、15、21等,小波去噪结合CVA-ICA的方法也具有良好检测效果。
4 结束语
考虑到工业过程含有噪声和随机干扰,以及过程变量较多且存在自相关性,文中提出了一种利用小波去噪结合CVA和ICA对动态多变量过程进行故障检测的思想,仿真结果表明,该方法较KPCA、ICA等方法可以有效的检测出各类故障。
参考文献:
[1]李元,谢植,王纲.基于故障重构的PCA模型主元数的确定.东北大学学报,自然科学版,2004,25(1):20-23.
[2]CUI P L,LI J H,WANG G Z.Improved kernel principal component analysis for fault detection.Expert Systems with Applications,2008,34(2):1210-1219.
[3]LEE J M,YOO C K,LEE I B.Statistical process monitoring with independent component analysis.Journal of Process Control,2004,14(5):467-485.
[4]LEE J M,YOO C K,LEE I B.Statistical monitoring of dynamic processes based on dynamic independent component analysis.Chemical Engineering Science,2004,59(14):2995-3006.
[5]CHIANG L H,RUSSELl E L,BRAATZ R D.Fault detection and diagnosis in industrial systems.London:Springer-Verlag,2001.
[6]赵旭.基于统计学方法的过程监控与质量控制研究[学位论文].上海:上海交通大学,2006.
[7]DONOHO D L,JOHNSTONE I.Wavelet shrinkage asymptopia.Journal of Royal Statistical Society,1995,57(2):301-369.
[8]NOUNOU M N,BHAVIK R.Bakshi.On-line multiscale filtering of random and gross errors without process models.AIChE,1995,45(5):1041-1058.
[9]胡友强,柴毅,李鹏华.在线多尺度滤波多变量统计过程的适时监测.重庆大学学报:自然科学版,2010,33(6):128-132.
[10]LEE C,CHOI S W,LEE I B.Variable reconstruction and sensor fault identification using canonical variate analysis.Process Control,2006,16(7):747-761.
[11]HSU Chun-Chin,CHEN,Mu-Chen CHEN.Long-Sheng Integrating independent component analysis and support vector machine for multivariate process monitoring.Computers & Industrial Engineering,2010,59(1):145-156.
[12]LEE Jong-Min,QIN S Joe.Fault detection and diagnosis based on modified independent component analysis.AIChE,2006,52(10):3501-3504.
[13]MUGDADI A R,AHMAD I A.A bandwidth selection for kernel density estimation of functions of random variables.Computational Statistics & Data Analysis,2004,47 (1):49-62.
[14]WANG J,QIN S.A new subspace identification approach based on principal component analysis.Process Control,2002,12 (8)841-855.
[15]DOWNS J J,VOGEL E F,Braatz R D.A plant-wide industrial process control problem.Computer & Chemical Engineering,1993,17(1):245-255.
[16]KU W,STORER R H,GEORGAKIS C.Disturbance dectection and isolation by dynamic principal component analysis.Chem.Intell.Lab.Syst,1995,30 (1):179-196.
[17]LEE J,YOO C,LEE I.Statistical monitoring of dynamic processes based on dynamic independent component analysis.Chem.Eng.Sc,2004,59 (14):2995-3006.
