并联电容式RF MEMS开关的系统级设计与分析
2014-03-21有德义郝永平
有德义,任 波,郝永平
(沈阳理工大学CAD/CAM技术研究与开发中心,辽宁沈阳 110159)
0 引言
RF MEMS开关是微电子机械系统(MEMS)发展的产物,它作为一种将传感、判断及执行于一体的微小器件。由于微加速度开关具有体积小、质量轻、生产批量化、成本低、集成化高、可靠性高等特点,被广泛应用在航空航天、汽车安全、消费电器、医疗器械及武器系统等领域[1-2]。
与目前射频系统中所用的电控开关(PIN二极管或GaAs FET)相比,RF MEMS开关采用微机械执行方式没有半导体PN结或金属半导体结,插入损耗很低(可小于0.2 dB,而PIN或FET的插入损耗总大于1 dB),隔离性能很好,互调失真极低,从直流至100 GHz范围都具有非常好的电气性能,隔离度和插入损耗同开关自身的结构参数密切相关[3]。为了得到更好的开关性能,在设计过程中有必要对射频MEMS开关的相关参数进行优化,实现MEMS产品的快速设计和性能验证。RF MEMS开关靠机械移动实现对信号传输线的开/断控制,工作于RF到mm波频段,其研究目的就是要提供低插损、高隔离、高线性、低功耗的新一代开关元件。RF MEMS开关有望集成在各种衬底上,包括带有有源半导体器件的衬底,可以增加人们对射频MEMS开关的研究兴趣[4]。
1 基本原理
在MEMS器件设计中,常用到静电驱动方式,优点在于结构简单、易于IC工艺集成、功耗低。简化开关力学模型如图1所示,假设在t=0时上极板静止,且上下极板受力平衡,此时,电压V0=0,间距H1=h,t>0时,当电压V(t),Fe作用时,开关梁发生形变,桥的位移Δh=h(t),开关梁仍然受力平衡。悬臂梁的弹性恢复力Fk=-kx和极板所受静电力Fe如下:
(1)
得到静态平衡方程和吸合电压为:
(2)
(3)
式中:Vpi为吸合电压;x为动极板运动距离;k为弹性系数;A为极板正对面积;V为偏置电压;ε0为极板间介质的介电常数;g0为极板初始间距。
图1为等效模型系统图,随着系统输入偏置电压越大,极板稳定位移范围越小系统最大加速度值越小,系统越容易进入非稳定状态。
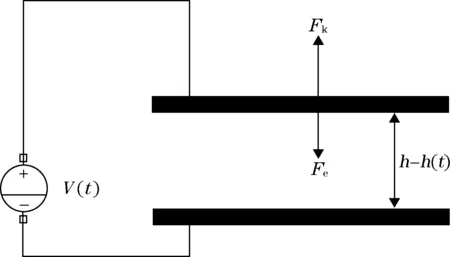
图1 等效模型系统图
2 并联RF MEMS开关的系统模型
微机电开关微机电部分的设计相当重要,由于开关的吸合电压不仅和开关的材料有关,而且和开关的结构尺寸工艺过程紧密相关,所以通过分析开关结构尺寸和驱动电压的大小之间的关系来优化设计结构尺寸,利用CoventorWare软件对RF MEMS开关分别进行工艺设计(图2)和系统级建模(图3)得到开关三维模型(图4)所示。

图2 开关的工艺步骤
系统级模型将整个系统看成是由不同能量域或多个同一能量域的基本单元组成的,每个单元为一个节点,相当于电路中基本元件如电容、电阻等。运用模拟硬件描述语言,将上述节点与真实电路连接在一起形成网罗,建立系统的微分方程模型。运用SABER进行系统仿真。
图4为RF MEMS开关的三维结构图,其中中介质层的材料是二氧化硅,主体梁的材料是多晶硅,接触导电的材料是金,上下层驱动电极的材料是镍。
3 系统模型分析与优化
3.1频域响应分析
在实际工作中,传感器谐振频率的大小决定了工作频率的范围,谐振频率越高,其相应的工作频率范围也就越宽。伯德(bode)图是通过对未知系统输入一系列频率不同的正弦信号,通过测量输出信号的幅值和相位,得到对应不同频率下,该系统对输入信号的幅值和相位,从而得到系统的内部结构。输出相对于输入只是振幅和相位发生了变化,而频率是不变的。而伯德图就是在输入的所有频率上,对该频率段区间取相应多的点,然后进行运算,算增益,算相位差,再转换成对数,然后可绘制出系统的伯德图的幅频响应曲线和相频响应曲线。利用CoventorWare中的Architect进行交流小信号分析,得到的伯德图如图4所示,当频率为9.849 6 kHz时,系统的幅频曲线出现最大值,即为可动电极Z向谐振频率,与有限元分析方法算得的一阶振型频率9.857 3 kHz接近,误差仅为0.078%.说明系统级分析不但运算速度比有限元分析方法快几十倍,而且运算准确精度高,研发周期缩短,商业价值高,是未来的发展趋势。

图3 Architect中的系统级模型
3.2直流转移分析
把射频开关抽象化,认为开关的执行方式是平行板电容器,把开关梁的机械回复特性抽象成一个悬挂在开关平板梁上的弹簧的弹性回复特性。
当给开关施加一定电压V(t),悬臂梁后端沿z轴方向产生形变或偏转,随着电压增加,悬臂梁的偏转程度也相应的增加。当梁偏转从0到h/3间距时,需要加的电压达到最大值;过了h/3间距之后,当梁的偏转程度进一步增加,需要使梁处于平衡位置的电压却开始单调减少,该转折点电压称为阈值电压。
由静电力作用产生的吸合效应会引起MEMS系统不稳定,限制众多静电驱动器的稳定运动范围,吸合电压是众多MEMS静电驱动器设计的基本参数。利用CoventorWare软件中的Architect进行吸合电压分析,吸合曲线如图6所示。上、下电极间隙为1.5 μm,当电压达到14 V时,可动电极与驱动电极之间产生吸合效应,即可动电极的吸合电压为14 V.当电压达到14.0 V时,可动电极的末端与下接触电极开始产生紧密接触,并一直保持闭合状态,如图5所示。为避免产生吸合效应给系统带来的不稳定,并联RF MEMS开关的电压工作范围应小于20 V.

图4 RF MEMS开关的三维模型

图5 幅频特性和相频特性
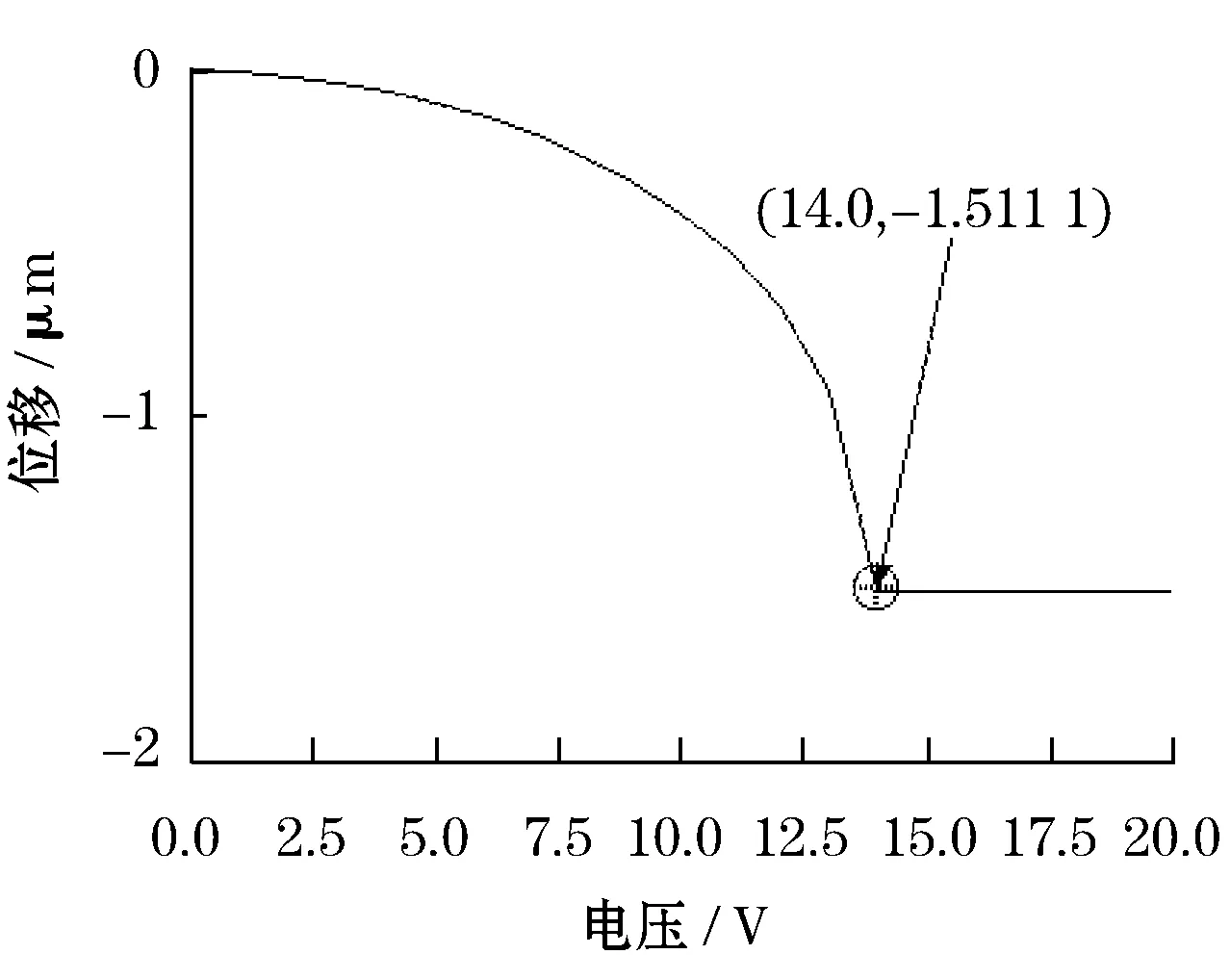
图6 电压与位移的关系曲线
4 有限元分析方法
可动电极的吸合和弹性结构释放涉及静电机械耦合问题。下面利用Coventorware软件中Analyzer的有限元分析模块MemElectro、MemMech和CoSolveEM,可以有效地分析静电-机械耦合场问题,在静电吸合模拟过程中为能够有效求出收敛解,将可动电极最大位移设置在距离其下表面1.5 μm处(即可动驱动电极和固定驱动电极之间的间隙),同时不考虑寄生电荷、粘附等十几种影响开关吸合和弹性结构释放的相关问题。
首先,利用CoventorWare软件中的Designer对生成的并联RF MEMS开关三维模型进行网格划分,划分后的有限元网格模型如图7所示。

图7 并联RF MEMS开关有限元模型
分析结果显示,在吸合过程中,电压从0开始,以0.5 V的步长线性递增到18 V,随着驱动电压逐渐增加,可动电极位移逐渐变大。可动电极吸合电压的范围在15.31~15.65 V之间,当驱动电压增加到15.31 V时,可动电极自由端运动位移超过间隙的1/3处,稍微再加一点电压,即可使可动电极的自由端与下接触电极相接触并一直保持闭合状态,并且随着驱动电压的增加,接触面积也逐渐增大。与Architect系统级吸合电压分析结果进行对比。有限元分析方法算得的吸合电压15.31 V与系统级分析方法算得的吸合电压14 V结果相差为1.31 V,误差率为9.37%。
5 结束语
针对并联RF MEMS开关通用性的要求,提出了这种系统级设计方法。利用CoventorWare软件中的Architect模块对开关进行系统级仿真,分析了系统的频率响应,同时也分析静电-惯性多物理耦合场对开关响应的影响,得到位移和电压的对应关系。说明系统级分析法不但运算速度快,而且运算准确、精度高,可见系统级分析法是未来的发展趋势。
参考文献:
[1]孟光,张文明.微机电系统动力学.北京:科学出版社,2008:189-190.
[2]陆逸敏.电容式RFMEMS并联开关的电磁干扰研究:[学位论文].南京:东南大学.2006.
[3]贾孟军,李昕欣,宋朝晖,等.开关点电可调节的MEMS冲击加速度锁定开关.半导体学报,2007,8(28):1295-1301
[4]BAO M H,HUANG Y P,YANG H,et al.Reliable operation conditions of capacitive inertial sensor for step and shock signals.Sensors and Actuators,2004,A114:41.
[5]GABRIEL M.Rebeiz.RF MEMS Theory,Design,and Techenology.John Wiley&Sons,Ine,2003.
[6]贾孟军,硅微机械加速度开关技术研究:[学位论文].上海:中国科学院(上海微系统与信息技术研究所) 2007.
[7]季国顺;张永康.微机械系统建模与仿真技术研究.光学精密工程,2002(06):626-631.
