透视三点问题贝叶斯解法(BP3P)及其推广

胡钊政 ，李 娜，夏克文

（1.武汉理工大学ITS研究中心，湖北 武汉 430063；2.河北工业大学信息工程学院，天津 300401）

透视三点问题(Perspective-Three-Point, P3P)是计算机视觉与摄影测量学领域经典问题，在目标定位、测量、虚拟现实、姿态估计等方向有重要和广泛的应用价值。P3P问题定义为：已知摄像机内参数矩阵，给定三点（又称控制点）在某参考坐标系的相对位置及其图像对应点，计算三控制点到摄像机光心的距离[1-14]。P3P是n点透视问题(PnP)中的其中一类问题，即n=3的情况。与其他PnP问题想比，P3P所需输入最少，应用更广泛。自其被提出以来，一直受到研究者们的重视。目前针对P3P问题的研究主要集中在两个方面：即P3P问题的具体解法与P3P问题解的分布情况。例如，P3P问题可以转化成以控制点距离为未知元的三组三元二次方程组的求解问题[1]，进而可以转成一元四次方程的求解问题[2]。Xu等[3]提出P3P问题的递归解法，Li和Xu等[4-5]提出P3P问题的稳定解法。许多学者研究了P3P存在多解的一般性条件。例如，Wolfe等[6]给出了P3P多解现象的几何解释，并指出P3P最多可以有4个不同的解，但大多数情况下有两个解。苏成和徐迎庆[7]给出了判断P3P正解数目的充要条件。张彩霞和胡占义[8-9]讨论了危险圆柱的情况。Gao等[10-11]运用Wu-Ritt零点分解方法研究P3P多解问题。Wu和Hu[12]通过计算旋转矩阵与平移矢量来求解P3P问题。符德林和马文鹏[13]扩展了P3P问题多解的判别条件适用范围。文中提出了透视三点问题贝叶斯新解法(Bayesian Perspective-Three- Point, BP3P)，为P3P问题的求解与分析提供了一条新的途径。算法不仅能求解P3P问题，还能对其解的分布情况进行分析。该算法将P3P问题转化成支撑平面计算问题。支撑平面的计算可以利用三控制点产生的角度，长度比例等约束条件，通过贝叶斯理论转化成最大似然概率估计问题。算法通过搜索高斯半球面来计算最大似然概率，确定支撑平面结构信息，完成P3P问题的求解，并对P3P多解现象进行分析。文中还将三控制点约束推广至一般性平面几何约束，实现单视图视觉定位，使所提的视觉定位算法具有较好的通用性。

1 P3P问题与支撑平面

1.1 支撑平面与P3P问题之间的关系

文中定义支撑平面(Support Plane)为三控制点所唯一确定的平面。针对支撑平面与P3P问题，有如下引理。

引理1确定支撑平面（即平面法向量和距离已知）是求解P3P问题的充要条件。

证明：a）必要条件证明

根据P3P问题的定义，每个控制点应满足如下约束条件：

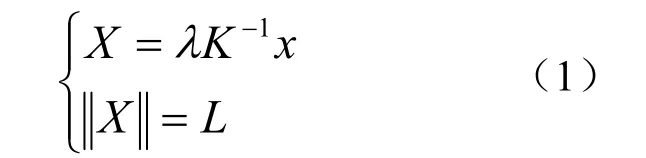
其中，第一个公式表示反向投影射线（见图1所示虚线），它可以通过控制点对应的图像与摄像机内参数矩阵K计算[14]。其中，λ为尺度因子。第二个公式表示控制点与摄像机光心之间的距离。若P3P问题已解，则控制点距离已知。通过式(1)可计算控制点三维坐标，并唯一确定支撑平面。必要条件得证。

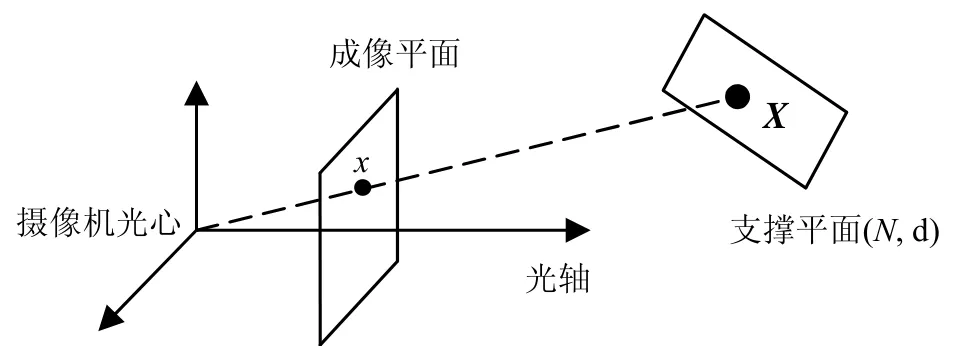
图1 控制点X，图像点x，支撑平面(N, d)与摄像机坐标系之间的几何关系

b）充分条件证明

每个控制点同时在其反向投影射线与支撑平面上，因此满足：

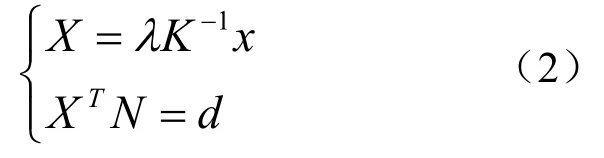
其中，N与d分别为支撑平面对应的单位法向量与距离（见图1）。若已知支撑平面，则可通过上式计算控制点三维坐标，并计算控制点与摄像机光心之间的距离，从而求解P3P问题。充分条件得证。

引理2P3P问题的多解对应为支撑平面的多解。

证明：若P3P问题存在多解对应为支撑平面的多解，即每组解对应不同的支撑平面。

通过上述两个引理，可将P3P问题转化成支撑平面求解问题。下文将提出BP3P算法来求解支撑平面。

1.2 从三控制点产生几何约束

假定小孔成像摄像机模型，根据射影几何理论，空间平面与其图像之间几何关系可以用单应矩阵来描述[14]：

旧时史书和方志的这种编纂方式，自有它存在的合理性，今人也不用过多苛责，但这一体例有与生俱来的重大缺陷，也就是人物形象的类型化，语言表述的格套化，对此，在方志学素有心得的章学诚也清醒地意识到这个问题：“行皆曾、史，学皆程、朱，文皆马、班，品皆夷、惠，鱼鱼鹿鹿，何以辨真伪哉？”［1］《修志十议》，844“称许之间，漫无区别，学皆伏、郑，才尽班、扬，吏必龚、黄，行惟曾、史。且其文字之体，尤不可通，或如应酬肤语，或如案牍文移，泛填排偶之辞，间杂帖括之句，循名按实，开卷茫然。”［1］《永清县志阙访列传序例》，776

其中，x与X分别为平面上的点与其对应的图像点（以齐次坐标表示），单应矩阵为一3×3的满秩矩阵。若已知单应矩阵，则可以通过图像点来计算该点在平面上的坐标。根据计算出来的坐标值，可以进一步计算出平面上的诸如长度、角度、面积、曲率等更多的几何属性。单应矩阵可以通过摄像机内参数矩阵与平面结构信息（平面法向量与距离）计算得到。计算方法可参考Liebowitz和Zisserman[15]提出的分层重建方法或Zhang[16]提出的基于世界坐标系设定方法。需要指出的是，如果平面法向量已知而平面距离未知，可假设平面距离为单位一，这样计算出来的物理平面上的坐标值及长度等几何属性与真实值在相差一个比例因子下相等。但是一些几何属性如角度、长度比例等与真实值相等（参考分层重建理论中的相似重建与欧氏重建的区别[14]）。若平面法向量已知，则可以利用参考长度确定平面距离（见后文所述）。因此，在平面法向量计算中主要考虑诸如角度，长度比例这些在相似变换中保持恒定的几何属性。因为P3P问题中摄像机内参数已知，因此这些平面几何属性的计算完全依赖于平面法向量。从而，可以用Q(N)来表示从给定法向量N计算出来的平面几何属性。

通过控制点坐标可计算三段线段长度（即点与点之间的距离），记为Di(i=1, 2, 3)。根据3个距离可计算三组长度比例：

同样的，亦可通过余弦公式计算得到3个角度。这三组长度比例与3个角度可以通过P3P问题的已知条件直接计算得到，因此它们是场景先验知识。利用这六组先验知识可对支撑平面产生六组几何约束，其数学表达如下：

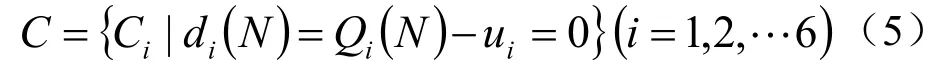
Qi(N)表示从平面法向量N计算得到的第i个平面几何属性值，ui为上述长度比例或角度，它们的差值di(N)定义为平面法向量N对应的校正误差。迫使校正误差为零，即可对支撑平面的法向量产生约束。

2 P3P问题贝叶斯解法(BP3P)

2.1 最大似然概率模型

将平面法向量计算转化为最大化条件概率问题。即给定六组几何约束，计算产生最大条件概率的平面法向量，其数学表达如下：

直接求解式(6)较困难，可利用贝叶斯公式将式(6)转化为：

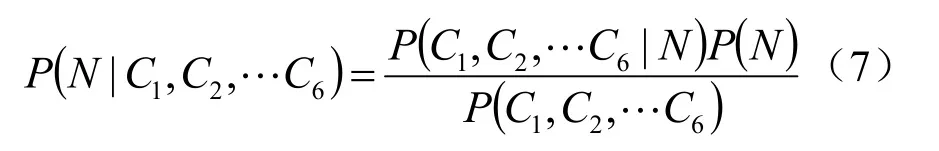
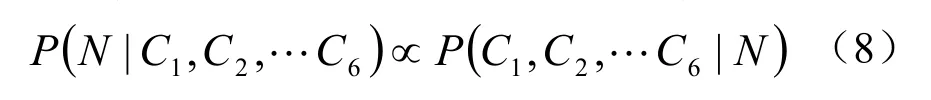
假设各几何约束之间条件独立，可将上式进一步转化成：

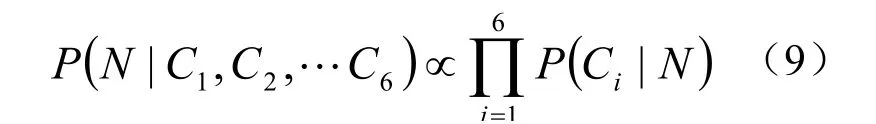
2.2 高斯似然概率模型

为了对似然概率进行准确的建模，提出了以下3个基本准则：

（1）校正误差决定准则。似然概率随着绝对校正误差增加而降低。当校正误差为零，则似然概率应取得最大值；

（2）几何约束对等性准则。若所有的几何约束被完全满足时（即校正误差为零），应产生相等的似然概率；

（3）归一化准则。即考虑到几何约束的表达形式、单位、尺度等差异，应将校正误差进行归一化处理。

基于上述准则，提出利用归一化高斯函数似然概率建模方法，其数学表达如下：

其中，校正误差用式(5)中ui（非零值）进行归一化以满足准则三。不难发现，式(10)可以满足准则一。为了满足准则二，所有几何约束应所对应的高斯函数应取相同的均方差，即σi=σj=σ，实际应用中可根据需求选择合适的均方差。从而有：

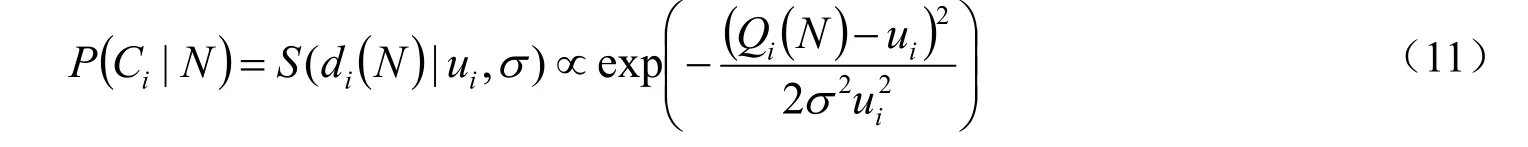
将式(11)代入式(9)可得：

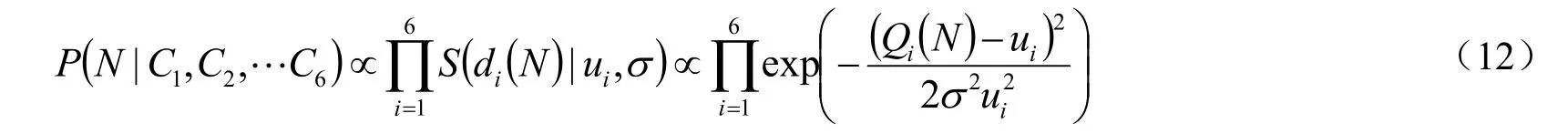
2.3 最大似然搜索

将式(12)代入式(6)可得：

文中采取全局搜索算法来求解式(13)。因为三维空间中单位法向量对应为三维高斯球面(Gaussian Sphere)上的一点，以此可将搜索区间确定为高斯球面。考虑到只有在摄像机前面的目标才能出现在图像中（即深度值为正的约束），可将搜索区间减半，在高斯半球面上搜索(Gaussian Hemisphere)。具体实现如下：首先在高斯半球面上均匀抽样[17]，每一个抽样点都对应一单位法向量。然后利用式(13)计算每个抽样点对应的似然概率，最后计算出最大似然概率对应的平面法向量即为支撑平面的法向量。需要指出的是，最大似然搜索能获得P3P的一个解，如果要获得P3P问题的多解，则需对计算出来的似然概率图进行相应的分析（见实验部分相关讨论）。

2.4 计算平面距离与控制点距离

若平面法向量已知，可假定平面距离为单位一，在相差一个尺度因子β下计算控制点三维坐标：

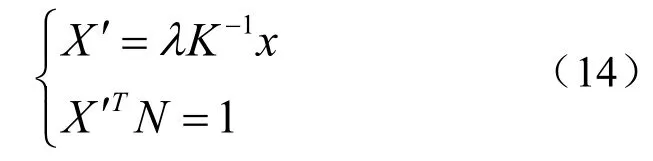
比较式(14)与(2)可知：X=βX′，且β为支撑平面的距离。利用任意两控制点的实际距离Di，可计算尺度因子β：

其中，为从式(14)计算的三维坐标得到的两个控制点之间的距离。确定尺度因子β，即可计算控制点实际距离完成P3P问题求解。

2.5 一般性几何约束的视觉定位

可以将BP3P算法推广用以处理更一般的几何约束，实现对平面目标的准确定位。实际上，文中算法仅要求场景的几何约束可以表达成式(5)的形式，就可以利用所提算法计算支撑平面，进行三维定位。例如，算法可以利用已知的角度，长度比例，甚至更一般性的几何约束条件，通过归一化高斯函数来对似然概率建模，计算最大似然概率，求解平面法向量。因此，三控制点仅是几何约束条件中的一个特例。除三控制点几何约束之外，算法可以处理更为一般性的几何约束，具有较好的通用性。考虑到实际环境中几何约束的多样性，文中所提BP3P算法具有更好的实用性与灵活性。

3 实验结果与分析

文中设计了三组实验来对所提BP3P算法进行验证。第一组实验中，考虑到计算结果如平面法向量与控制点距离的基准值(Ground Truth)很难获取，文中采用Zhang[16]标定算法中所用到的标定模板作为支撑平面，通过在平面上随机选择3个不共线的网格点作为三控制点（见图2中Δ标记所示）。选择标定模板的主要原因有二：

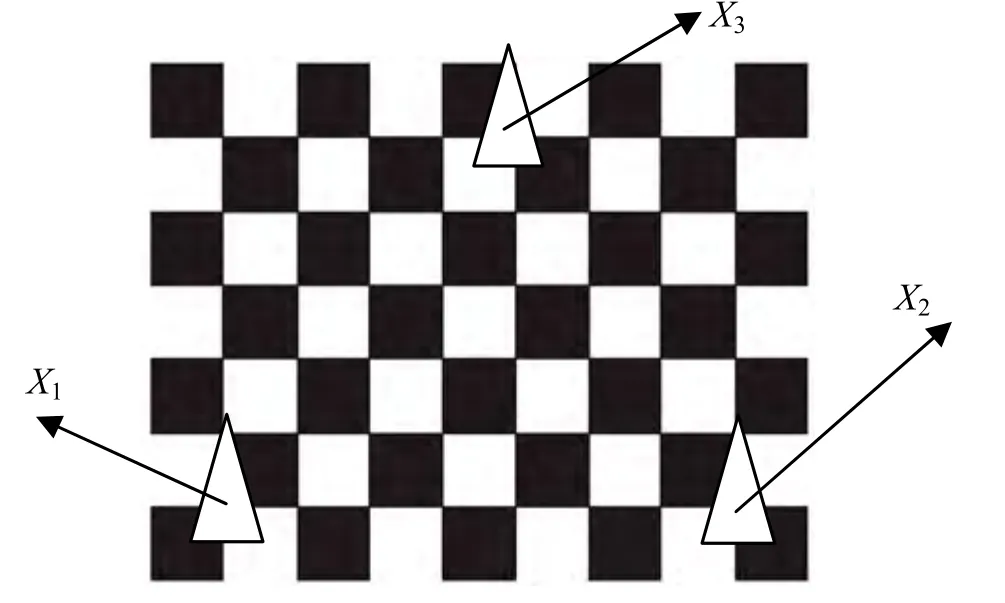
图2 在平面网格中随机选择3个非共线控制点X1, X2, X3

（1）可以准确地标定出摄像机的内参数，并将其作为P3P问题所需的部分输入条件；

（2）可以将标定结果的摄像机外参数（如旋转矩阵和平移矢量）作为基准值，对计算结果进行验证。利用Nikon Coolpix 4100数码相机从不同角度和位置拍摄标定模板的照片。部分图像如图3所示，图像分辨率为1600×1200（像素）。利用Zhang[16]平面模板标定算法计算得到摄像机焦距为4175.2，主点位置在 [874, 677]T（单位皆为像素）。

图3 平面网格模板在不同位置与角度下拍摄的图像

首先用文中BP3P算法计算支撑平面在不同图像中的法向量。在高斯半球上抽取200×400个采样点来离散化搜索区间，通过搜索最大似然概率来计算平面法向量，并将其与基准值进行比较。用计算得到的法向量与基准法向量之间的夹角来表示法向量计算误差。计算结果见表1所示。其中，第二行与第三行分别为文中算法计算得到的支撑平面单位法向量和从摄像机标定结果中计算出来的基准值，第四行为两个法向量对应的角度误差。从表1计算结果可以得到：四幅图像中计算出来的法向量与基准值最大误差为0.33°，平均误差为0.25°，表明计算结果较稳定和准确。

表1 支撑平面法向量计算结果

根据表1中计算出来的法向量，通过任意两个控制点之间的实际距离作为参考长度来计算支撑平面的距离，从而确定支撑平面。最后利用式(2)来计算每一个控制点在摄像机坐标系的三维坐标Xi(i=1,2,3)，最后计算控制点在四幅图像中与摄像机关心的距离。计算结果见表2所示。表2中分别用表示文中算法计算的距离与距离基准值，并用表示距离计算误差。根据表2中结果可得：控制点与摄像机光心的距离分布在1.0～2.2m之间，距离最大计算误差为0.8cm，平均误差为0.4cm。这些计算结果表明BP3P算法具有较好的精度和稳定性。

表2 控制点与摄像机光心的距离计算结果(cm)

实验中还利用BP3P算法来分析与求解P3P多解问题。如引理2所述，P3P多解对应为支撑平面的多解。考虑一个包含两个解的P3P问题[6]，利用BP3P算法进行展示。如图4所示，图4(a)为原始图像，图4(b)为从6个几何约束计算得到的似然概率图。图中用灰度值表示似然概率，灰度值越大，似然概率越大。从图中可以明显观察到似然概率有两个峰值区域。图4(c)为对似然概率图进行分析的结果。利用阈值将似然概率图进行分割以凸显似然概率最大的30个平面法向量的位置，可以发现它们分布于两个区域。在两个区域中分别计算局部最大似然概率，可以求解支撑平面法向量的两组解，分别为[0.0699-0.8883 0.4540]T，[-0.0917 0.8019 0.5904]T。它们在似然概率图中对应的位置见“+”所标记。根据计算的两组平面法向量，可以获得P3P问题的两组解。因此，BP3P算法不仅可以求解P3P问题，同时还能对其多解情况进行分析。

图4 利用BP3P算法分析P3P的多解问题

第二组实验中，对BP3P算法进行推广，利用一般性几何约束实现视觉定位。如图5所示，图5(a)为利用Nikon D700拍摄的原始图像数据，图像分辨率为2218×1416，摄像机的焦距为1369.0（单位皆为像素）。考虑到实际场景中有各种各样的几何约束，实验中很难对它们进行一一探讨，因此文中采用两种代表性的几何约束（即已知的角度与长度约束）对算法进行验证。实际上，很多特定的几何约束也可以进一步转化成角度或者长度的形式（如上文所讨论的P3P问题）。如图5(b)所示，通过墙面上标准A4纸上点与线之间的关系得到三组几何约束：即L1与L2，L3与L4之间的夹角，以由M1，M2和M3，M4所确定的线段长度比例（见图5(b)所示）。算法首先利用这三组约束条件来求解A4纸所在平面的单位法向量。

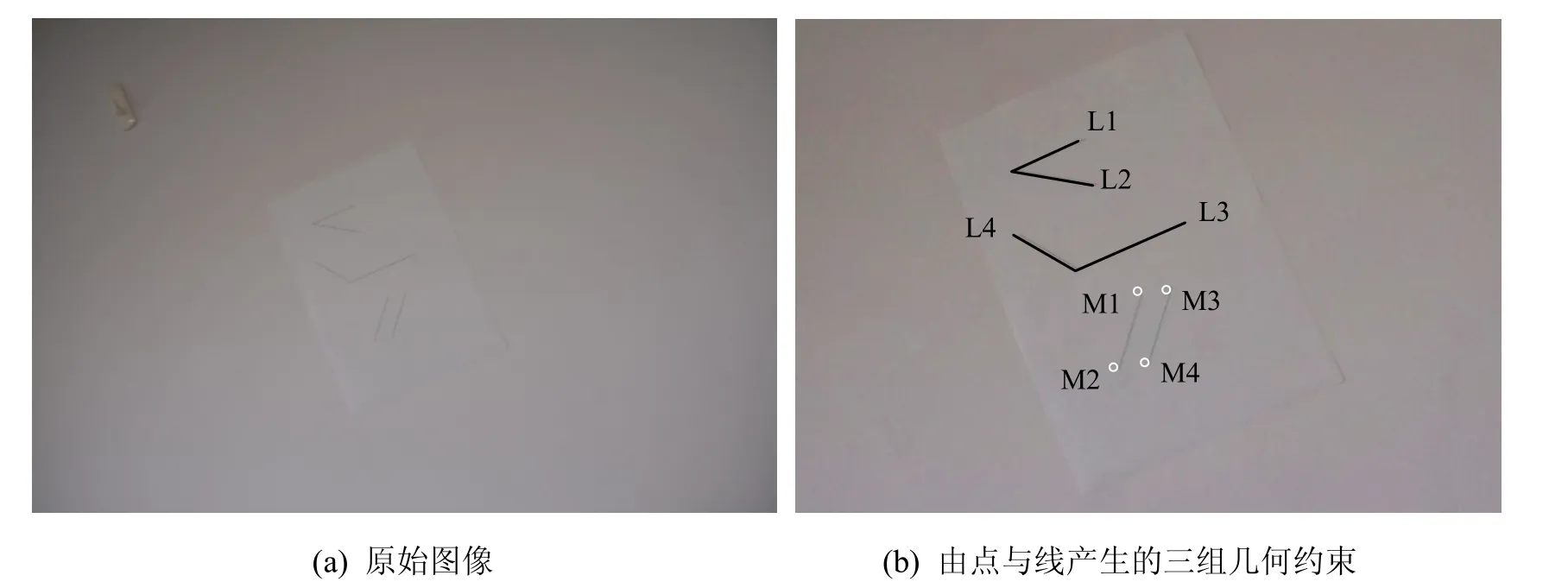
图5 一般性几何约束用于视觉定位

如图6所示，图6(a)～(c)分别表示3个几何约束所产生的似然概率图，其中图像灰度值越大表示似然概率越大。从图6(a)～(c)可以观察到：三组几何约束产生的似然概率是非均匀分布，并且各个约束对应的概率分布图皆不相同。图6(d)表示三组几何约束产生的联合似然概率，在图右下角可很明显观察到一个极大概率分布区域。图6(e)显示似然概率最大的30个平面法向量对应位置，可以观察到它们共同分布在一狭小区域（见白色所标记的区域）。图6(f)显示了似然概率最大的平面法向量所在的位置（用‘+’标记），其对应的平面法向量为 [0.0993 0.1679 0.9808]T。

图6 利用BP3P算法从三组一般性几何约束条件计算平面法向量

以A4纸长度（图7中P1～P2距离）作为参考值计算实际平面距离，然后计算平面上点的三维坐标。实验中，从六组线段中抽取一定数目的点进行定位。此外，还对A4纸的4个顶点进行定位（见图中所标记P1～P4四点）。它们在摄像机坐标系中对应的三维坐标如图7所示。利用A4纸张的标准尺寸（210mm×297mm）对算法计算结果进行验证。利用计算出来的三维坐标计算P2～P3，P3～P4，以及P1～P4之间的距离，分别为206.7mm, 294.6mm, 211.8mm。与A4纸张的标准尺寸比较，绝对误差分别为 3.3mm, 2.4mm,1.8mm，对应的相对误差水平分别为1.6%,0.8%,0.9%。这些结果表明计算结果较准确，所提BP3P算法能被推广，用以处理一般性几何约束，实现准确的视觉定位。

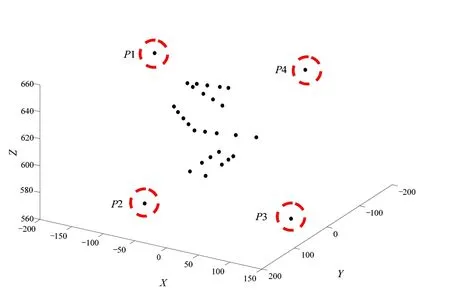
图7 平面点三维定位结果(mm)（P1～P4为A4纸4个角点）

第三组实验中，对BP3P进一步推广与验证，利用一般性几何约束实现室内环境下的视觉定位。室内尺寸为6.5m×6.5m，其中墙上所挂白板平面的高度为1.2m。如图8(a)所示，左图为利用Coolpix 4100数码相机拍摄的原始图像数据，图像分辨率为2248×1712，摄像机的焦距为2356.7（单位皆为像素）。从场景中选取已知的三组长度比例及3个角度作为一般性几何约束条件。其中，三组长度比例分别由图中4个点（见图中Δ标记）所确定的长度定义。3个角度为三条虚线（如图所示）所确定，分别为90°, 90°, 0°。这些约束条件产生的似然概率如图8(b)所示，采用的高斯面分辨率为200×400。通过搜索最大似然概率，计算对应的平面法向量为[-0.5030.112-0.857]T（见图8(a)中‘+’所标记的位置）。而通过场景中的平行线等信息计算出来的平面法向量为[- 0.5000.092-0.861]T[14]。两者之间的夹角误差仅为1.2°，表明了文中所提的算法具有较好的精度与实用性。

图8 利用一般性几何约束进行室内视觉定位

4 结论

针对计算机视觉领域经典的P3P问题，文中提出了P3P问题的贝叶斯新解法(BP3P)，为P3P问题的求解与分析提供了一条新的途径。首先证明支撑平面是求解P3P问题的充要条件，提出了基于贝叶斯的支撑平面计算方法，将平面法向量估计问题转化成最大似然概率问题。利用高斯函数来对几何约束进行似然概率建模，在高斯半球面上搜索最大似然概率，确定支撑平面。用实验对算法进行验证，结果表明BP3P算法可以准确求解P3P问题并分析其多解现象。在一米至两米距离之内，平面法向量与距离平均计算误差分别为0.25°和0.4cm。实验中，BP3P算法还被推广用以处理一般性几何约束，实现对平面目标的准确定位，从而使所提的视觉定位算法具有较好的通用性。研究结果具有一定的理论与应用价值。

[1]Fischler M, Bolles R.Random sample consensus [J].Communications of the ACM, 1981, 24(6): 381-395.

[2]Long Quan, Lan Zhongdan.Linear N≥4 point camera pose determination [J].IEEE Transaction on Pattern Analysis and Machine Intelligence, 1999, 21(8):774-780.

[3]Xu De, Li You, Tan Min.A general recursive linear method and unique solution pattern design for the perspective-n-point problem [J].Image and Vision Computation, 2008, 26(6): 740-750.

[4]Li Shiqi, Xu Chi.A stable direct solution of perspective-three-point problem [J].International Journal of Pattern Recognition and Artificial Intelligence, 2011, 25(11): 627-642.

[5]Li Shiqi, Xu Chi, Xie Ming.A Robust O(n) solution to the perspective-three-point problem [J].IEEE Transaction on Pattern Analysis and Machine Intelligence, 2012, 34(7): 1444-1450.

[6]Wolfe W, Mathis D, Sklair C, Magee M.The perspective view of 3 Points [J].IEEE Transaction on Pattern Analysis and Machine Intelligence, 1991, 13(1):66-73.

[7]苏 成, 徐迎庆.判断P3P正解数目的充要条件[J].计算机学报, 1998, 21(12): 1085-1095.

[8]Zhang Caixia, Hu Zhanyi.Why is the danger cylinder dangerous in the P3P problem? [J].Acta Automatica Sinica, 2006, 32(4): 504-511.

[9]张彩霞, 胡占义.P3P问题的多解现象的概率研究[J].软件学报, 2007, 18(9): 2100-2104.

[10]Gao Xiaoshan, Hou Xiaorong, Tang Jianliang, Cheng Hangfei.Complete solution classification for the perspective-three-point problem [J].IEEE Transaction on Pattern Analysis and Machine Intelligence, 2003,25(8): 930-943.

[11]汤建良.一类P3P问题方程系统的零点分解[J].数学的实践与认识, 2004, 34(8): 124-127.

[12]Wu Yihong, Hu Zhanyi.PnP problem revisited [J].Journal of Mathematical Imaging and Vision, 2006,24(1): 131-141.

[13]符德林, 马文鹏.P3P问题多解条件的补充研究[J].计算机工程与应用, 2011, 47(2): 179-181.

[14]Hartley R, Zisserman A.Multiple view Geometry in Computer vision (2nd Edition) [M].Cambridge, UK:Cambridge University Press, 2004.

[15]Liebowitz D, Zisserman A.Metric rectification for perspective images of planes [C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 1998: 482-488.

[16]Zhang Zhengyou.A flexible new technique for camera calibration [J].IEEE Transaction on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.

[17]Leopardi P.A partition of the unit sphere into regions of equal area and small diameter [J].Electronic Transactions on Numerical Analysis, 2006, 25(12):309-327.