基于微分进化算法的非对称弧齿锥齿轮约束多目标优化

钱学毅，迟建华，吴 双

（1.武夷学院电子工程系，福建 武夷山 354300；2.大连开发区大开产业发展研究中心，辽宁 大连 116600；3.浙江经贸职业技术学院应用工程系，浙江 杭州 310018）

对弧齿锥齿轮传动进行约束多目标优化设计是提高产品设计质量、缩短产品设计周期、提升产品市场竞争力的有效手段。传统的格利森制弧齿锥齿轮是按照齿面两侧具有相同啮合性能的原则进行对称设计。但在工程实践中，大部分传动装置如汽车等正转一侧齿面的使用率大大高于另一侧。因此，为充分利用材料，研究弧齿锥齿轮强度的非对称设计（在反转齿面用一个小的压力角、在正转齿面使用一个较大的压力角）即可以提高齿轮的齿根弯曲强度、齿面接触强度和胶合强度又可以有效地避免齿顶过分变尖的现象，具有工程实用意义。文献[1-2]提出了设计双压力角非对称齿廓齿轮的思想，用以在发挥大压力角优点的同时又可避开轮齿两侧压力角同时增大会导致齿顶强度和柔度下降，抗冲击能力降低，加载时容易崩齿等缺点。文献[3]提出了在准双曲面齿轮轮坯设计中，摒弃强度的对称设计，修正正转用齿面的压力角，以增加正转用齿面的强度，减少齿根拉应力。

本文在上述设计思想的基础上，根据齿轮啮合原理和现代摩擦学理论，建立了以弧齿锥齿轮传动齿面上瞬时接触线方向与相对滑动速度之间夹角的余切值最小、传动总体积最小和齿面诱导法曲率主值最小为目标函数的约束多目标优化设计数学模型。借助于改进的微分进化多目标优化算法，利用MATLAB编制优化程序，通过范例对非对称弧齿锥齿轮传动进行两目标和三目标优化设计。并分析了齿面上瞬时接触线方向与相对滑动速度之间夹角及齿面诱导法曲率主值对齿面接触强度和胶合强度的影响，为其综合性能的进一步优化提供基础。

1 齿面上瞬时接触线方向与相对滑动速度之间的夹角

接触线方向与相对运动速度之间的夹角θ在齿轮啮合中是一个很重要的角度。它对于两齿面在相对运动时形成润滑油膜的条件有很大的影响。根据弹性流体动力润滑理论中的Dowson-Higginson线接触最小油膜厚度公式[4]

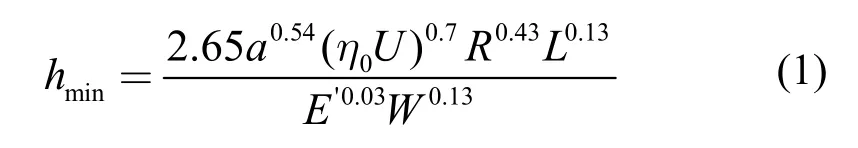
式中：hmin—最小油膜厚度(mm)

a—润滑油的黏压系数(MPa-1)

η0—润滑油的动力黏度(MPa·s)

U—卷吸速度(mm/s)

R—当量曲率半径(mm)

L—两齿面接触线的长度(mm)

—齿轮材料综合弹性模量(MPa)

W—齿面间的法向载荷(N)

从上式中可见，最小弹流油膜厚度与卷吸速度（即形成油膜的有效速度）有关，卷吸速度越大，最小膜厚越大，润滑条件越好，抗胶合能力和抗磨损能力越强。卷吸速度等于相对滑动速度在与接触线垂直方向上的分量。因此，为了有利于形成油膜，改善润滑条件，接触线方向与相对运动速度之间的夹角θ应尽可能的大。依据齿轮啮合原理

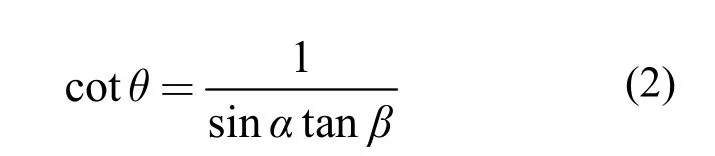
式中：α—法向压力角(o)

β—螺旋角(o)

显然，由式(2)计算的值cotθ越小越好。

2 弧齿锥齿轮齿面诱导法曲率主值

根据微分几何理论和齿轮啮合原理，两相啮合齿面在切点沿同一个方向的法曲率之差称为该方向的诱导法曲率，是相对曲率，它刻划了两啮合齿面在该方向上相对弯曲的程度，也就是切点沿同一方向的邻近点相对离开的快慢程度。共轭齿面的诱导法曲率是衡量齿轮传动质量的一个重要指标，该值越小，说明两接触齿面在这个方向上相对弯曲的程度越弱，当量曲率半径越大，Hertz弹性接触应力越小，接触强度越高，同时Hertz应力的减小还使齿间最小油膜厚度增加，抗胶合承载能力得以提高。

过啮合齿面上的某一切点，沿不同的方向，具有不同的诱导法曲率，必有一个最大值和一个最小值，其最大值和最小值称为诱导法曲率主值。取得主值的方向称为主方向，两个主方向具有正交性。

弧齿锥齿轮在传动时是线接触，两齿面在接触线方向τ的诱导法曲率等于零，这是它的一个主方向。诱导法曲率的另一主方向与接触线方向τ垂直，设这个方向的诱导法曲率主值为kσ，则kσ是最大值，用式(3)计算[5]：式中：σk—诱导法曲率主值(mm-1)

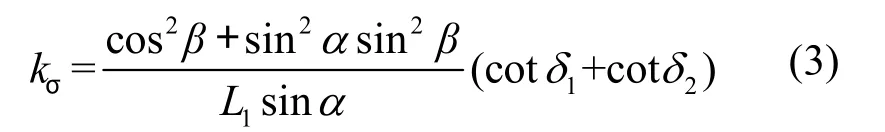
δ1,δ2—小轮、大轮的分度锥角(o)L1—小轮分度圆锥的锥距(mm)其他符号意义同前。

3 微分进化约束多目标优化算法

微分进化算法(Differential Dvolution, DE)是近来提出的简单而高效的多目标进化算法，是一种采用浮点矢量编码的全局空间中进行随机搜索的优化算法。目前国内外对于多目标微分进化算法的研究尚处于起步阶段，相关研究主要集中在算法性能的改进与完善上。国外具有代表性的有Abbass[6]的自适应Pareto微分进化算法，Madavan[7]及Xue等[8]学者的基于Pareto最优概念的多目标微分进化算法。国内的研究主要有张利彪等[9-11]学者提出的基于极大极小距离密度的多目标微分进化算法。国内外学者的研究在一定程度上提高了多目标微分进化算法的性能，但这些研究还仅限于对数学测试函数的研究，还不能直接用来进行实际工程的优化设计，尚需要进行改进。

本文在对现有的微分进化多目标优化技术进一步研究的基础上，针对其在机械工程设计中存在的问题，提出了相应的策略，改进了现有的微分进化多目标优化技术，给出了基于微分进化技术、适用于机械工程领域的约束多目标优化算法。

3.1 现有微分进化算法在机械设计中存在的问题

机械设计中的多目标优化设计往往是在复杂而苛刻的约束条件下进行。当利用现存的算法进行迭代时，会发生下面的问题：

（1）在进行变异和交叉操作产生的新个体有可能在可行域内，也有可能在不可行域内，而支配关系的比较和极大极小距离密度的计算都是在目标函数空间中进行的，不可行域内的个体产生的目标函数完全有可能支配可行域内的个体产生的目标函数，其密度值的计算也同样具有不确定性，这样删除的很可能将是有用的个体，保留的将是无用的个体。最后迭代出的结果很可能毫无意义。

（2）若变异和交叉操作只在可行域内进行，则每产生一个新个体都要进行可行性检验，满足约束条件则保留，不满足约束条件则罚掉，再重新搜索，直到满足约束条件为止。设计实践表明，复杂而苛刻的约束条件不但会使收敛速度慢得让人难以接受，而且约束边界上的目标个体还很容易使程序陷入死循环。例如，当进行齿轮设计时，若将齿数限定在20～50，当某一目标个体的齿数恰好是20或50时，用DE的变异和交叉产生新个体的操作就会使程序陷入死循环，导致优化设计无法进行。

3.2 基于极大极小距离密度实用多目标微分进化算法

为解决前述多目标微分进化算法所产生的问题，使迭代高速有效，避免程序进入死循环，提出基于极大极小距离密度实用多目标微分进化算法如下：

（1）设置初始参数：向量维度D、初始群体规模NP、缩放因子F、交叉常量CR、最终可行解规模N；

（2）在可行域内随机生成初始群体P，规模为NP；

（3）将群体P中的非劣解加入Pareto候选解集中；

（4）在无约束条件下，用DE的变异和交叉操作，对群体P和Pareto候选解集中的每一目标个体x都生成一个新个体x′；

（5）对每一个新个体x′都进行可行性检验，满足约束条件的保留，否则直接罚掉；

（6）将所有目标个体和满足约束条件的新个体一起构成群体T；

（7）如果Pareto候选解集的规模没有达到规定的大小，将所获得的非劣解直接加入到Pareto候选解集中，直到达到候选解集的设定规模；否则，比较个体间的支配关系，保留支配个体，丢弃被支配个体，直到达到候选解集的规模；如果所有被支配个体都丢弃以后，候选解集的规模仍超过设定值N，则计算Pareto候选解集中每一个体的极大极小距离密度，并删除密度值最大的个体，直到达到候选解集的设定规模；

（8）如果满足中止条件，停止迭代，否则返回（4）。

4 范 例

非对称弧齿锥齿轮传动的承载能力和传动性能与下面的两个因素密切相关：

（1）接触线方向与相对运动速度之间的夹角θ；

（2）齿面诱导法曲率主值。接触线方向与相对运动速度之间的夹角θ越接近于90o，齿面诱导法曲率主值越小，承载能力越高，传动性能越好。因此非对称弧齿锥齿轮传动优化设计是在满足约束条件下寻求cotθ最小及齿面诱导法曲率主值最小，同时还要寻求齿轮传动总体积最小（最经济），是一个约束多目标优化问题，多目标没有公度性，不宜用传统的多目标优化方法来处理。这是因为传统的多目标优化方法是将多个目标通过加权求和转化为单目标问题进而进行优化。这样做有以下缺点：

① cotθ无量纲，齿面诱导法曲率主值(mm-1)，总体积(mm3)，各目标单位不一致，无可比性；

② 多个目标加权值的分配带有较大的主观色彩，难以反映客观真貌；

③ 优化目标仅为多个目标的加权和，优化过程中各目标的优度进展不可操作；

④ 多个目标之间通过决策变量相互制约，存在相互矛盾，致使加权目标函数的拓朴结构十分复杂。改进的微分进化技术在解决此类问题中得到成功应用。

4.1 已知数据

主动齿轮的转速n1=960r/min，被动齿轮的转速n2=320r/min，传递的功率P=100kW；选用齿轮油HL-30润滑，其运动黏度ν100=30mm2/s；油池温度θoil=50℃；两轮齿面粗糙度分别为Ra1=Ra2=0.8μm。

4.2 选取向量维度D

选取7个设计变量（D=7）

式中，z1为主动轮齿数；mt为端面模数；α、β意义同前；xt为主动轮切向变位系数；x为主动轮高变位系数；b为齿轮宽度(mm)。

4.3 建立目标函数

（1）将齿轮传动总体积最小作为一个追求的目标，即

式中，dm1、dm2分别为两齿轮中点的分度圆直径(mm)。

（2）将齿面上瞬时接触线方向与相对滑动速度之间夹角的余切值最小作为第二个追求的目标，即

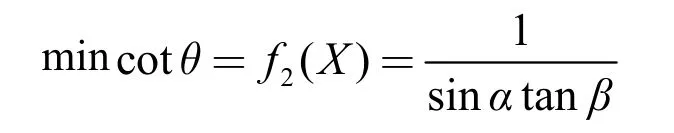
（3）将齿面诱导法曲率主值最小作为同时追求的第3个目标，即

4.4 确立约束条件

参照文献[12-13]及工程实际经验确立胶合强度约束、接触强度和弯曲强度可靠性约束、齿顶厚约束、齿数约束、模数约束、压力角约束、螺旋角约束、变位系数约束、齿宽约束等。

4.5 优化计算及结果遴选

用MATLAB进行程序设计计算，设置初始参数：D=7、NP=50、F=0.3、CR=0.5、N=100，循环200次，结果得到100组可行解及相应的目标函数值。以f1(X)和f2(X)为目标函数的两目标优化非劣最优目标域如图1所示。根据程序运行结果，从中选取2个目标函数都接近最小值，综合性能最佳的一组结果，本例中选取图1中左下边界点（决策者也可根据自己的偏好选择其他的结果）作为最终方案：X*=[z1,mt,α,β,xt,x,b]T=[12,4, 24.6202, 39.4660, 0.7541, 0.2268, 50]T，总体积V=1.5237×105mm3，齿面上瞬时接触线方向与相对滑动速度之间夹角θ的余切值f2(X)=cotθ=2.9154，θ=18.93°。以f1(X)、f2(X)和f3(X)为目标函数的3目标优化非劣最优目标域如图2所示。最终方案为：X*=[z1,mt,α,β,xt,x,b]T=[12, 6, 25.8226, 39.8978, 0.8567, 0.5570,17]T，总体积V=2.0980×105mm3，齿面上瞬时接触线方向与相对滑动速度之间夹角θ的余切值f2(X)=cotθ=2.7459，θ=20.01°，齿面诱导法曲率主值f3(X)=kσ=0.0409mm-1。

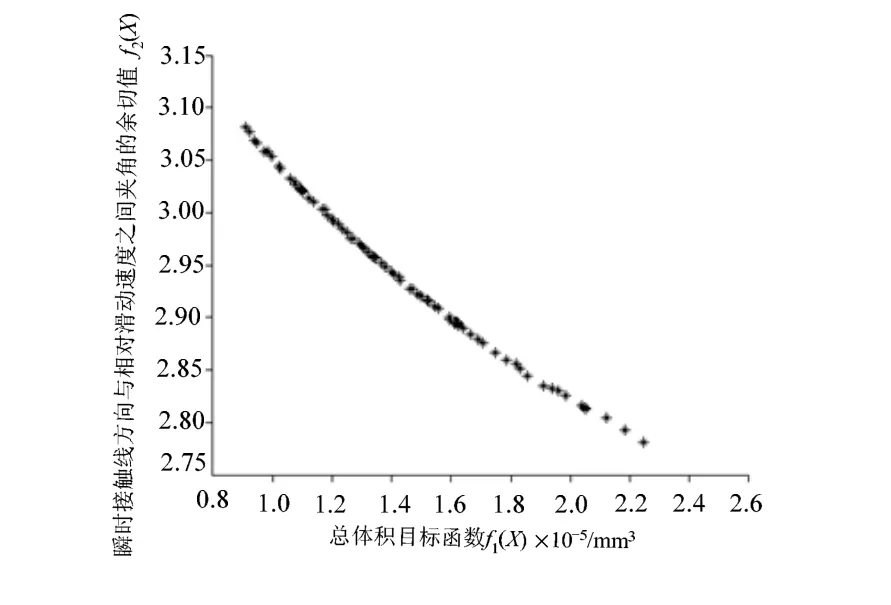
图1 两目标优化非劣最优目标域

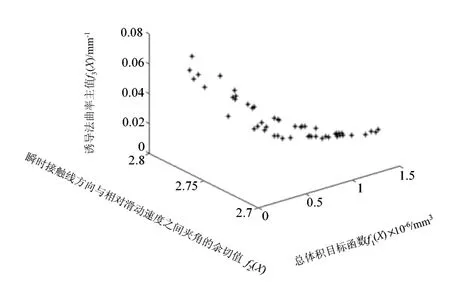
图2 三目标优化非劣最优目标域

4.6 用粒子群算法进行优化并与微分进化算法做比较

用粒子群优化算法(particle swarm optimization, PSO)[14-15]，参照文献[16-18]中提出的寻优原则和搜索方法对本算例进行优化。粒子群规模为100，进行200次迭代，所得非劣最优目标域如图3所示。比较图1和图3可以看出，微分进化算法个体的多样性和收敛性都好于粒子群算法。优化实践表明，微分进化的收敛速度更是远远大于粒子群算法，群体规模都是100，同样都是MATLAB编程，同一台计算机上都是运行200次循环，微分进化仅用了35分钟，而粒子群算法则用了20.8个小时，这是由于：

（1）粒子群算法受约束条件的限制，随着循环次数的增加，在可行域内搜索新粒子的速度会越来越慢，而DE算法在寻求新个体的过程中不考虑约束条件，不必反复迭代；

（2）PSO算法在寻求新粒子时需要考虑粒子的历史痕迹，而DE算法不必顾及个体进化的历史痕迹，只需考虑当前状态即可，相对来讲，DE优化程序简单，计算量小，PSO程序复杂，计算量大。

图3 PSO非劣最优目标域

5 结 论

（1）本文给出了基于极大极小距离密度多目标微分进化算法的改进策略，并将改进的微分进化算法用于弧齿锥齿轮的多目标优化设计，成功地验证了改进算法的有效性，该方法比传统的多目标优化方法及目前常用的其他现代优化方法都具有明显的科学合理性和实用性。

（2）本文给出的弧齿锥齿轮传动系统多目标优化设计方法和得到的设计参数，能有效地提高产品的设计质量，提升产品的综合经济技术指标。该方法进一步拓展了微分进化算法的工程应用领域，对于其他复杂机械传动系统的约束多目标优化设计也具有一定的参考价值。

[1]Litvin F L, Fuentes A, Howkins M.Designing,generation and TCA of new type of asymmetric face-gear drive with modified geometry [J].Computer Methods in Applied Mechanics and Engineering,2001, 190(43-44): 5837-5865.

[2]Difrancesco G, Marini S.Structural analysis of asymmetrical teeth: reduction of size and weight [J].Gear Technology, 1997, 14(5): 121-125.

[3]张金良, 方宗德, 邓效忠, 吴 斌.准双曲面齿轮强度的非对称设计[J].机械科学与技术, 2005, 24(5):568-602.

[4]温诗铸, 黄 平.摩擦学原理[M].北京: 清华大学出版社, 2002: 73-75.

[5]吴序堂.齿轮啮合原理[M].西安: 西安交通大学出版社, 2009: 293-296.

[6]Abbass H A.The self-adaptive pareto differential evolution algorithm [C]//Proc of the Congress on Evolutionary Compution (CEC’2002).Piscataway:IEEE Service Center, 2002: 831-836.

[7]Madavan N K.Multiobjective optimization using a pareto differential evolution approach [C]//Proc of the Congress on Evolution Computation (CEC’2002).Piscataway: IEEE Service Center, 2002: 1145-1150.

[8]Xue F, Sanderson A C, Graves R J.Pareto-based multi-objective differentil evolution [C]//Proc of the 2003 Congress on Evolutionary Computation(CEC’2003).Piscataway, NJ: IEEE press, 2003:862-869.

[9]张利彪, 许相莉, 马 铭, 孙彩堂, 周春光.基于微分进化求解多目标优化问题中的退化现象[J].吉林大学学报(工学版), 2009, 39(4): 1041-1046.

[10]张利彪.基于粒子群和微分进化的优化算法研究[D].长春: 吉林大学计算机科学与技术学院, 2007:92-110.

[11]张利彪, 周春光, 马 铭, 孙彩堂.基于极大极小距离密度的多目标微分进化算法[J].计算机研究与发展, 2007, 44(1): 177-184.

[12]秦大同, 邢子坤, 王建宏.基于动力学和可靠性的风力发电齿轮传动系统参数优化设计[J].机械工程学报, 2008, 44(7): 24-31.

[13]齿轮手册编委会.齿轮手册[M].北京: 机械工业出版社, 2005: 5-9-5-134.

[14]Kennedy J, Eberhart R.Particle swarm optimization [C]//IEEE International Conference on Neural Networks:Perth, Australia.Piscataway.NJ: IEEE Service Center,1995: 1942-1948.

[15]Eberhart R, Kennedy J.A new optimizer using particle swarm theory [C]//Roc.Sixth International Symposium on Micro Machine and Human Science:Nagoya, Japan.Piscataway, NJ: IEEE Service Center,1995: 39-43.

[16]魏静萱.解决单目标和多目标优化问题的进化算法[D].西安: 西安电子科技大学, 2009: 73-77.

[17]张 敏.约束优化和多目标优化的进化算法研究[D].合肥: 中国科学技术大学, 2008: 9-15.

[18]张利彪, 周春光, 马 铭, 刘小华.基于粒子群算法求解多目标优化问题[J].计算机研究与发展,2004, 41(7): 1287-1290.