变形Rikitake双盘耦合发电机系统的动力学分析与控制

雷腾飞，陈 恒，王 荣，任林政，孟 敬

（西京学院研究生部,陕西 西安 710123）

变形Rikitake双盘耦合发电机系统的动力学分析与控制

雷腾飞，陈 恒，王 荣，任林政，孟 敬

（西京学院研究生部,陕西 西安 710123）

以Rikitake双盘发电机为研究对象，结合工程中的机电系统，重写该系统的数学模型．验证了在一定范围与外部输入条件下双盘发电机会产生混沌与极限环现象．利用极点配置方法对系统的混沌运动进行控制, 因此具有很好的动态响应特性．仿真结果验证了理论分析的正确性与控制方法的有效性．

双盘发电机；混沌控制；状态反馈

1 引 言

上世纪60年代，lorenz在天气预报的模型中发现了“蝴蝶效应”，从此许多科研工作者走进了非线性研究领域中有关混沌的研究[1].

混沌现象在工程中普遍存在,尤其在电机系统中[2-13].1958年Rikitake首先提出的双盘发电机的模型曾作为最早解释地磁的起源与地磁场长期变化中极性反转现象的模型，为此地磁理论中需要且最难说明的问题得以解决.文[14]验证了该模型含有丰富的混沌现象.近几年，双盘发电机的模型已应用到工程中，文[15]对该系统的混沌运动进行了分析，且采用比例微分方法控制，但很难在工程与实际系统中实现.自1990年Ott、Grebogi和Yorker提出控制混沌的思想以来，混沌控制的方法与理论不断涌现.现阶段对于永磁同步电机的控制方法已经有很多报道与研究[10-13]，但对于具体双盘发电机混沌系统甚至变形的双盘发电机有效的控制方法报道却还不多，在众多的控制方法中采用一种有效的控制方法，使系统避免混沌产生显的极为重要且具有现实意义[14].

本文针对双盘发电机混沌系统，结合工程中机电耦合系统，重新建立变形双盘耦合发电机模型.利用相位图、分岔图，Lyapunov指数等分析了该混沌系统的基本动力学特性，验证了其丰富的混沌动力学行为；在考虑控制方法能够有效的应用到工程及实际背景下，本文采用极点配置控制方法对变形耦合发电机混沌运动进行了控制，并通过仿真对控制策略进行了验证.

2 变形双盘耦合发电机的数学模型与混沌特性

地磁学家Rikitake在1958年首次提出了双盘发电机的模型，双盘发电机由两个圆盘与两个耦合在一起的线圈组成.该模型的无量纲方程[15]

其中x1, x2表示无量纲的电流，x3表示两圆盘的角速度，µ和σ表示正的可调参数.

结合双盘发电系统，也为了研究工程中的耦合发电机，重新改写得到新的模型：

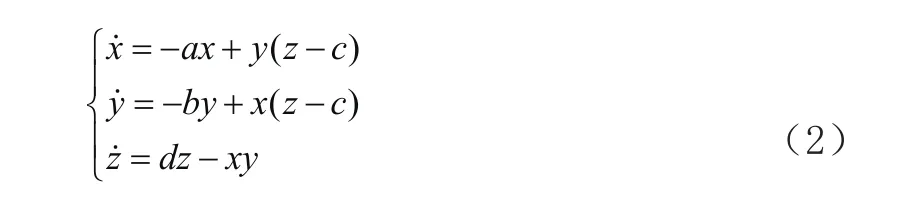
a和b、c、d表示正的可调参数.参数a=2，b=3，c=1，d=0.75，得到系统的吸引子，如图1.

2.1 耗散性

变形双盘耦合发电机系统的耗散性，由系统（2）导出：

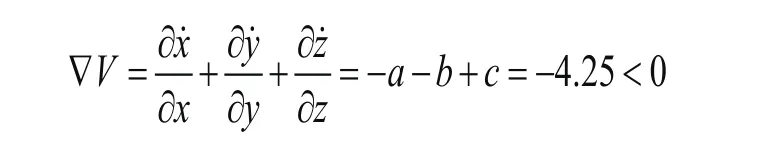
2.2 平衡点的稳定性

设系统(1)的平衡点为E0=(x0,y0,z0)为了方便书写，将平衡点分为两部分E10=(x10,y10,z10)，E20=(x20,y20,z20)=(0,0,0)

为了分析平衡点的稳定性[15]，可以得到平衡点E0的Jacobian矩阵：

将平衡点E0=(x10,x20,x30)代入式子（3） ，求出在此平衡点处的Jacobian矩阵的特征方程：

则求出三个根，有两个根是焦结点与一个鞍结点.根据稳定性判定可知，无论两参数取什么值，平衡点都是不稳定的.从图2可看出最大的Lyapunov指数大于零，说明系统（1）存在混沌行为[16].

图1 系统的吸收引子图Fig.1 Phase graph of system

图2 系统（1）Lyapunov指数谱Fig 2 Lyapunov exponent of system

2.3 参数对系统的影响

参数的变化，从系统的三个方向的Lyapunov指数和分岔图，可以直观看出系统运动状态的变化，下面就我们增加的两个参数下系统的Lyaunov指数与分岔图进行讨论研究.

参数a受环境，工作条件等因素影响比较大，随着参数a的变化系统呈现出非常丰富的非线性，当a∈[1,10]系统进入了混沌状态.

在实际工程中，参数d为磨损参数，现固定参数a=2，b=3，c=1,从图3（g）(h)可以看出，当d∈[0.2,1.1]系统出现了一个正的Lyapunov指数，系统处于混沌状态，分岔图也可以表明.当a∈(1.1,1.5]，混沌特征下降，还有段间隔区.最大的Lyapunov指数接近0，系统处于倍周期运动形式.

同理可以看出其他参数,通过分析可知，该系统易处于混沌状态.当系统处于混沌运动时，电流与电压忽高忽低，这很容易引系统的崩溃，通过对参数分析，改变参数是很难将其脱离混沌.因此须找一种合适有效的方法消除或抑制系统中混沌行为.

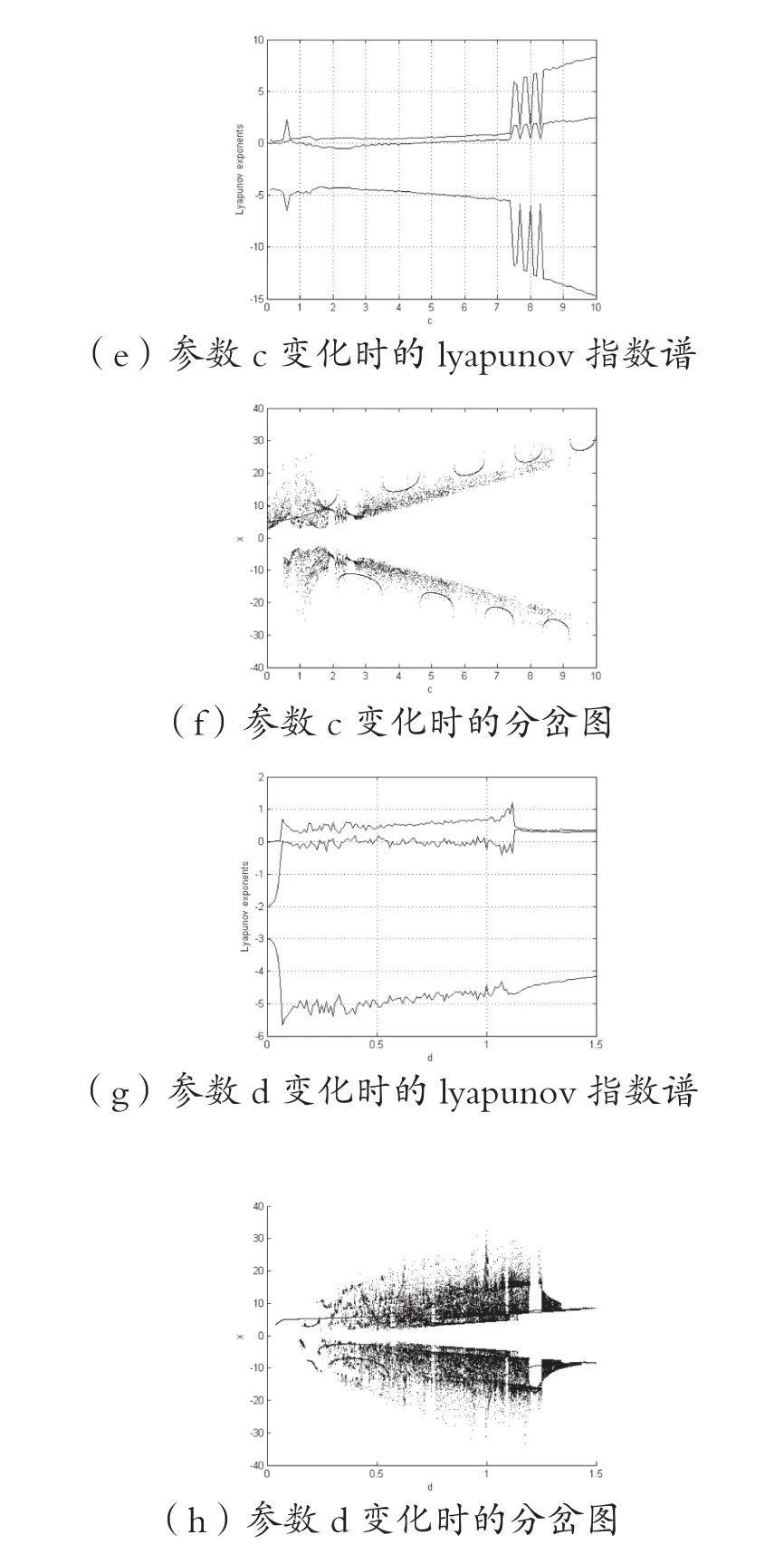
图3 系统的分岔图与参数变化Lyaunov指数谱Fig.3 Lyapunov exponent and Bifurcation diagram of system

3 双盘发电机混沌运动的状态反馈控制

3.1 非线性系统的状态反馈控制理论

考虑如下不受控的非线性自治系统：

其中X为状态变量，α为参数；在平衡点附近处线性化，则系统（5）近似为：

其中B为对角矩阵，μ为控制向量，且

其中，K为反馈增益矩阵.

K矩阵的求解，本文利用控制论中极点配置的方法来确定，从而使系统达到稳定状态[17].

3.2 控制器的设计

根据上述理论，考虑系统（1）加入状态反馈控制项，u=K( X−E0)，则系统（1）的受控系统为：

根据（7），可以简化 ，B=diag(1,1,1) .

则系统（9）在系统（1）平衡点E0下的Jacbian矩阵为：

则受控系统的特征方程：

其中，A1, A2,A0都是与k1, k2, k3有关系数.

取希望配置的极点(−1,−1,−10)，则极点构成的特征多项式为[17]：

极点的特征多项式(12)与受控系统的特征多项式(11)相同，求出k1=9,k2=0,k3=7.75.当系统运行到10s时，加入控制，仿真的结果如图4，相位图如图5.从图4、5可以发现，在20s控制器参与工作后，系统迅速达到稳定状态，具有良好稳定性能.

图4 受控系统的运动状态Fig.4 States of controlled system

图5 受控系统的运动相位图Fig.5 Phase graph of controlled system

4 结 论

本文针对变形Rikitake双盘耦合发电机模型，研究表明模型在一定参数范围内系统具有混沌运动，此外，还分析了这种混沌的基本特性.针对该发电机混沌特性，应用状态反馈控制.并对整个系统进行了仿真研究，仿真结果表明系统在控制器的作用下能够迅速达到稳定状态，理论分析与数值仿真结果相一致.表明该控制系统设计不需要使用除系统状态变量以外的受控系统其他有关信息.研究结果说明该方法有效，且对工程具有重要的参考价值.

[1] 陈关荣,吕金虎.Lorenz系统族的动力学分析控制与同步[M].北京：科学出版社，2003.

[2] 马西奎，李明，戴栋,等. 电力电子电路与系统中的复杂行为研究综述[J]. 电工技术学报, 2006 ，21(12): 1-11.

[3] 张波，李忠，毛宗源.永磁同步电动机的混沌模型及其模糊建模[J].控制理论与应用, 2002, 19(6):841-844.

[4] 杨秀媛，肖洋，陈树勇. 风电场风速和发电功率预测研究[J].中国电机工程学报, 2005, 25(11): 1-5.

[5] 于东升，陈昊 ，卢胜利,等.开关磁阻调速电机混沌特征分析[J],电工技术学报,2010,25(10)：66-80

[6] 刘婷婷，谭彧，吴刚，等. 基于SVPWM的高转速永磁同步电机控制系统的研究[J].电力系统保护与控制,2009,37(12): 11-14.

[7] 王玲芝.改进的永磁同步电机直接转矩控制系统仿真实现[J]. 电力系统保护与控制, 2009, 37(19): 65-69.

[8] 吴忠强,奥顿.线性连续系统混沌跟踪控制的T-S模型方法[J].电机与控制学报, 2007,11(2): 201-206.

[9] 陈敏，李泽军，黎昂. 基于混沌理论的城市用电量预测研究[J]. 电力系统保护与控制, 2009, 37(16): 41-45.

[10] 刘栋梁, 郑谢辉, 崔丽丽. 无速度传感器永磁同步电机反推控制[J]. 电工技术学报，2011，26(6): 67-72.

[11] 陈振, 耿洁, 刘向东. 基于积分时变滑模控制的永磁同步电机调速系统[J].电工技术学报,2011,26(6): 56-61.

[12] 王宏佳, 徐殿国, 杨明,等. 永磁同步电机改进无差拍电流预测控制[J]. 电工技术学报, 2010, 26(6): 39-45.

[13] 闫光亚,艾武,陈冰,等. 永磁直线同步电机ADRC控制系统[J]. 电工技术学报,2011, 26(9): 60-66.

[14] I Keisuke . Chaos in the Rikitake two disk dynamo system [J]. Earth and Planetary Science Letters , 1980 , 51(2):451-456.

[15] 常迎春，刘晓君，李险峰. Rikitake双盘发电机模型的混沌与控制[J].辽宁师范大学学报（自然科学版），2006.29（4）：422-426.

[16] 王发强,刘崇新. Liu混沌系统的混沌分析及电路实验的研究[J]. 物理学报, 2006, 55(10):5061-5069.

[17] 于常官.现代控制理论[M].哈尔滨：哈尔滨工业大学出版社，1997:111—115.

（责任编辑 程 杰）

On Chaotic Analysis and Control of the Modified Rikitake Two-disk Dynamo

LEI Tengfei，CHEN Heng，WANG Rong，REN Linzheng ，MENG Jing
( Xijing University, Xi’an 710123, China)

Suited to the nonlinear system of Rikitake Two-disk Dynamo , the system can exhibit a variety of chaotic or limit cycle phenomenon under some choices of system parameters and external inputs. A state variable feedback controlling or suppressing chaos. The control system is excellent in the dynamic response performance, Because of the feedback gain determined by pole placement method. The simulation results demonstrate the effectiveness and realizable of the proposed methods. The research results will provide theoretical

for the study of improving control performance.

two-disk dynamo；chaos control；state variable feedback

TM315

A

1004—1877（2014）03—052—05

2014-01-18

雷腾飞（1988—），男，山东肥城人，硕士，研究方向：混沌电路系统与控制，电机控制.

陕西省科学技术研究发展计划项目（2009k0940）；西京学院科研基金（XJ20130117）