方差分析在激光点光源质量评价中的应用
2014-03-20安其昌张景旭
安其昌,张景旭,杨 飞,郭 鹏
(1.中国科学院长春光学精密机械与物理研究所,吉林长春130033;2.中国科学院大学,北京100049)
1 引言
激光点光源由于相干性好、能量强在各种光学系统的检测与装调中,都有较为广泛的应用。大多数波前检测元件,使用前,都需要点光源作为初始的标定工具,同时,如果在点光源之前加上特定的补偿光学元件,就可以将其发出的球面波转化为需要的波前。如在一代哈特曼传感器之前,附加分光棱镜与点光源,就可以检测球面镜的低阶面形误差;将上述装置应用于主动光学的定标之中,也有较好的效果[1-15]。
由于激光点光源常常作为光学系统的标校工具,故对于其本身的误差需要严格的控制。传统上,一般使用精度较高的波前探测元件直接测量,通过波前的均方根来评价点光源发光的均匀性,这样的方法将所有的误差源都作为随机误差,难以对于系统误差的水平做出合理的判断[16-19]。
方差分析是英国统计学家费歇尔在上个世纪所提出的,最初用于分析农产品产量的变化是由于随机误差还是因为品种改良,后来逐渐应用于其他各个领域。其核心思想是:在重复以及随机化的前提下,将采集到的数据看作由理想值与随机误差相加合成得到,之后利用假设检验来权衡分析其变异情况。对于点光源发光质量评价,将多次测量得到的数据合理的排布,就会出现和麦田类似的情况,每一个像元得到的数据,相当于一株麦子的产量,利用方差分析,就可以得到激光点光源波前的系统误差以及随机误差情况。
本文类比农产品产量分析的方法,引入方差分析来研究激光点光源的系统误差以及随机误差。利用维纳过程理论推导了理想激光点光源的统计学模型为高斯分布;之后,针对一种检验激光点光源发光均匀性的检测方法并进行了实验验证。本文的工作对于点光源的发光质量评价有着一定指导意义;同时,对于光电系统的误差分析也有很好的帮助作用。
2 基本推导
对于点光源所产生的绝对理想的波前,测量仪器不可避免的检测误差,也会对数据产生不规则的影响;另一方面,由于在实际的操作过程中的不可控因素(比如大气湍流的扰动以及隔振效果不理想),实际得到的波前数据也是由各种不规则的起伏构成。系统经过去除掉低阶波像差之后,分析其波前信息的过程与分析随机过程的方法类似。
维纳(Wiener)过程是爱因斯坦(Einstein)对于布朗运动进行分析时,建立的数学模型。其本质在于针对不规则运动内部的数学规律进行了提炼,下面将参考维纳(Wiener)过程对于点光源波前误差进行分析。
首先考虑无系统误差的情况,按照维纳过程的基本假设,在测量范围内,假定起始点的波前误差为零,同时点光源波像差具有下述性质:
(1)波像差各坐标分量都是独立的,考虑其中一个分量,记为w(l),对于任意相互不相交的区域,
有:w(d1)- w(u1),w(d2)- w(u2),…,w(dn)-w(un),都相互独立。
(2)理想的误差应为对称分布,因而E{(w(l)}=0。
(3)w(l+Δ)-w(l)的分布与l无关,并且σ2(Δ)=E{(w(l+Δ)-w(l))2}存在且是Δ的连续函数。
设w(l)的分布密度函数为f(l,x)其特征函数:
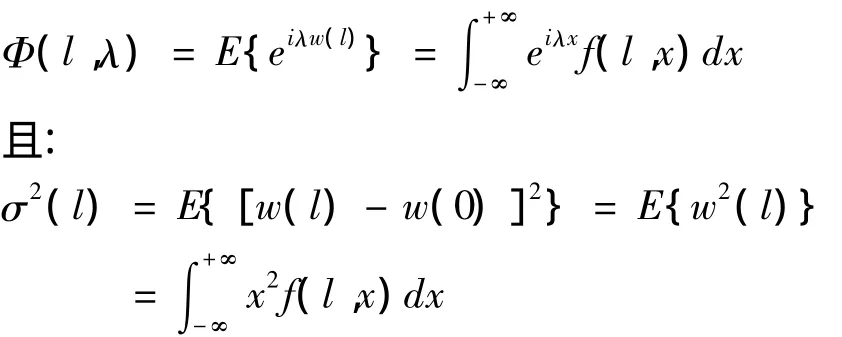
那么:
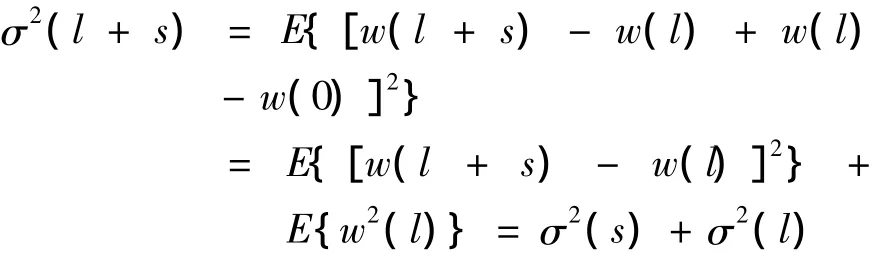
连续性可得:

又:

令s→0

由式(1)可得较为理想的点光源波像差应服从高斯(Gauss)分布,由于系统带有系统误差,假设检测得到的数据为 Φij=i+ δij,(j=1,…,n;i=1,…,k),其中i表示水平i的理论平均值,称为水平i的效应,即像素i的系统波像差;而δij表示随机误差,服从式(1)所表示的分布。
对于点光源光源质量评价,关心的是i是否相同,如果相同通过去除低阶piston可以得到完全理想的波前,即点光源的系统误差不显著;在实际的应用中,“显著”指的是与随机误差比较,系统误差达到了一定程度,而对于程度的定量分析,需要进行假设检验。
所要检验的假设为:H0:1=2=… =n
设总平方和为:
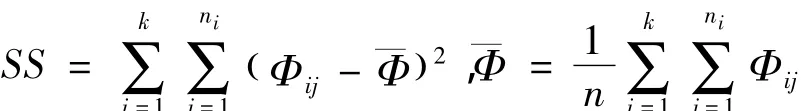
将总平方和分为两部分,一部分表示由随机误差带来的影响记为SSe,另一部分为各个水平的理论平均值之间的差异所造成的影响,即系统误差,记为SSA。对于SSe做进一步的分析:固定一个i,考虑其一切观察值,他们之间的差异完全是由随机误差所造成,故可以将 SSe表示为:SSe=,通过两者之差可以得到:
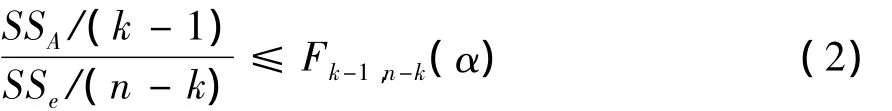
通过以上分析可得:对于较为理想的点光源,系统随机波像差服从高斯(Gauss)分布,同时各个像元对应的波像差,应该有相近的系统波像差,即造成测量差异的主要是随机误差。
下面一节将结合理论分析,利用假设检验的方法,提出一种对于实际点光源发光质量的评价方案。
3 方案设计、验证与应用
对于口径较小的系统,该方法可以作为复检检具精度或者高精度测量时的方法,而对于大口径系统,由于光学器件的尺寸以及光路的长度增加的原因,该方法成为了误差分配与分析时需要考虑的问题。
首先考虑小口径系统直接测量的情况,对于实际的点光源,需要进行多次测量,每次测量时都需要微量移动点光源,并重新校准一次。八邻位是图形处理中经常使用的位置关系,一般来说得到像素点周围八个点的信息,就可以较为全面的评价该像元,故为了尽量完整全面地分析点光源的发光质量,需要至少进行九次测量,对应原点、四个象限及其角平分线。下面对于本文得到方法进行实验验证。
本文使用PHASICS公司所生产的剪切干涉仪作为波前探测元件,其原理不同于使用微透镜阵
由于δij服从高斯分布,故利用假设检验,得到接受H0时,有:列进行波前斜率测量的一代哈特曼波前传感器,而是利用可以分离四个相位的衍波板,可以做到多像元,大视场测量快速测量;在测量之前,首先将点光源调节至剪切干涉仪的测量光轴,并进行一次数据采集,结果如图1所示,根据之前的方法,所有数据的平均值以及像素方差数据如图2和图3所示。

图1 波前测量数据Fig.1 data ofwave - frontmeasurement
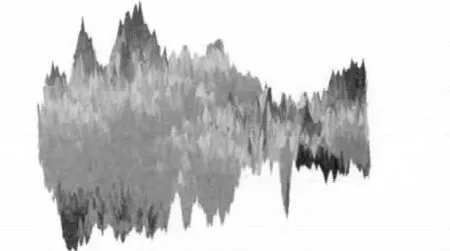
图2 所有数据平均Fig.2 Average of all the data

图3 各个像素点标准差数据Fig.3 Data of standard variance of piexl
将以上数据代入式(2)可得:

由以上分析可得,在置信概率0.99下,可以接受激光点光源的系统误差是均匀的,而对于随机误差的评价需要结合具体的误差分配来讨论。
对于下一代大口径光电系统,30米望远镜(TMT)计划由美国加州理工学院(Caltech)、加州大学系统(UC)和加拿大大学天文研究联盟联合发起。其中中国承担的三镜系统主镜为椭圆形平面镜,长轴为3.594 m,短轴为2.536 m。对于如此巨大的平面镜反射系统,传统上使用的检测技术以及误差分配标准已经不再适用,需要利用子孔径拼接与扫描技术。对于不同的检测方案,都需要一个标准而理想的光源,对于如此巨大口径的系统的放大作用,对于检测系统标准光源的随机特性的要求会大幅升高。将符合前文分布的随机误差叠加到TMT三镜仿真面形数据之上,如图4所示,可以看出对于系统波像差造成了明显影响,而小口径系统(如镜面上的一个小的子孔径),影响就比较小。具体的定量误差分配需要进一步的分析与分配。这将是之后工作的重点。
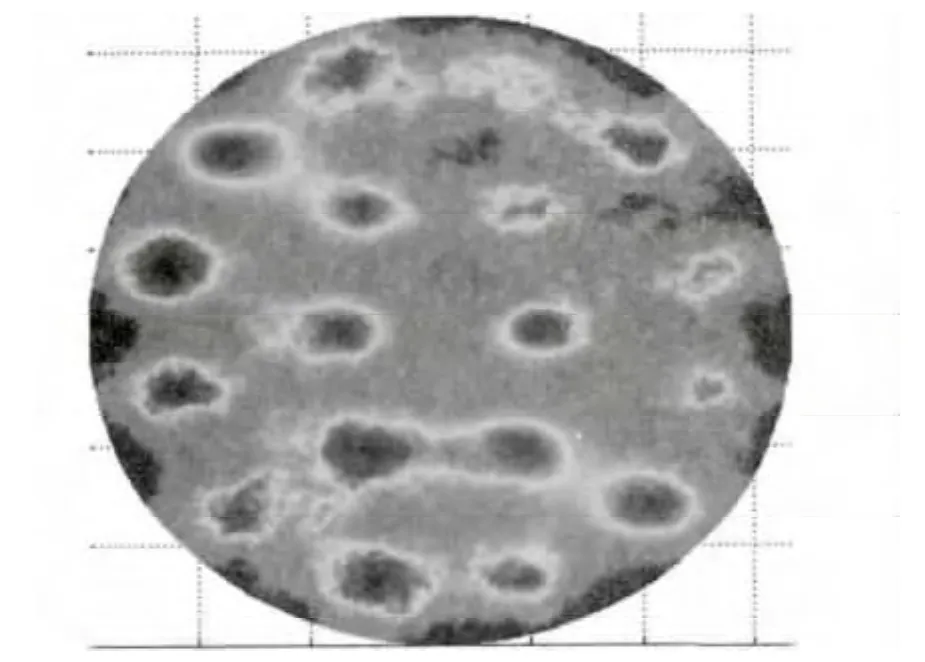
图4 TMT三镜波前Fig.4 Wave front of TMTM3
4 总结
本文引入方差分析来研究激光点光源的系统误差以及随机误差。利用维纳过程理论推导了理想激光点光源的统计学模型为高斯分布;之后,对于小口径系统,提出了一种检验激光点光源发光均匀性的检测方法。对于大口径系统(如TMT),具体的定量误差分配需要进一步的分析与分配。这将是之后工作的重点。本文的工作对于光电系统的误差分析与分配有很好的指导作用。
[1] WANG J,WANG Z F,SUIQ M.Study of FBG stain distribution based on improved genetic algorithm dual constraint[J].Chinese Journal of Lasers,2012,39(3)03050041 -0.050046.(in Chinese)王静,王正方,隋青美.基于改进遗传算法双重约束的应变分布重构研究[J].中国激光,2012,39(3)03050041 -0.050046.
[2] ZHANG LM,ZHANG B,YANG F.Design and test of force actuator in active optical system[J].Opt.Precision Engineering,2012,20(1):38 -44.(in Chinese)张丽敏,张斌,杨飞.主动光学系统力促动器得设计和测试[J].光学 精密工程,2012,20(1):38 -44.
[3] BIY,ZHAI J,WU JH,et al.Onemethod formirror surface figure treatment in optical instrument[J].Optical Technique,2009,35(1):10 -17.(in Chinese)毕勇,翟嘉,吴金虎,等.一种光学仪器镜面面形的处理方法[J].光学技术,2009,35(1):10-17.
[4] WANG D,YANG H B,CHEN C ZH.Computer simulation of the optical surface[J].Computer Simulation,2007,24(2):298 -301.(in Chinese)王栋,杨洪波,陈长征.光学表面面形的计算机仿真[J].计算机仿真.2007,24(2):298 -301.
[5] ZHANGW,LIU JF,LING FN,et al.Study on wavefront fitting using Zernike polynomials[J].Optical Technique,2005,31(5):675 -678.(in Chinese)张伟,刘剑峰,龙夫年,等.基于Zernike多项式进行波面拟合研究[J].光学技术,2005,31(5):675 -678.
[6] LIN X D,LIU X Y,WANG JL,et al.Performent of correction capability of 137-element deformablemirror Opt[J].Precision Engineering,2013,21(2):267 - 273.(in Chinese)林旭东,刘欣悦,王建立,等.137单元变形镜的性能测试即校正能力实验[J].光学 精密工程,2013,21(2):267-273.
[7] ZHANGJX.Overview of structure of technologies of large aperture ground based telescope[J].Chinese Optics,2012,5(4):327 -336.(in Chinese)张景旭.地基大口径望远镜系统结构技术综述[J].中国光学,2012,5(4):327 -336.
[8] NIM Y,GONG Y.Design and analysis of kinematic lens positioningstructure in lithographic projection objective[J].Chinese Optics,2012,5(5):476 - 483.(in Chinese)倪明阳.巩岩光刻投影物镜光学元件运动学支撑结构的设计与分析[J].中国光学,2012,5(5):476-483.
[9] SHAO L,YANG F,WANG FG,WU X X.Design and optimization of supporting system for1.2m lightweight SiC primarymirror[J].Chinese Optics,2012,5(3):229 -234.(in Chinese)邵亮,杨飞,王富国,吴小霞.1.2 m轻量化SiC主镜支撑系统优化设计[J].中国光学,2012,5(3):229-232.
[10] A novel predictive controller in the adaptive optics control system based on parallelization method[J].Acta Optica Sinica,2012,32(8):080100501 - 081001511.(in Chi-nese)史晓雨,冯勇,陈颖.一种基于并行化方法的自适应光学闭环预测控制器[J].光学学报,2012,32(8):080100501-081001511.
[11] WANG R D,WANG P,TIAN W.Design and analysis of compensation of large aperture optical element for gravity deformation[J].Chinese Optics,2011,4(3):259 - 263.(in Chinese)王汝冬,王平,田伟,等.大口径光学元件重力变形补偿的设计分析[J].中国光学,2011,4(3):259-263.
[12] WU Xiaoxia,WANG Minghao,MING Ming,et al.Calibration of thermal distortion for large aperture SiC lightweight mirror[J].Opt.Precision Engineering,2012,20(6):1243 -1249.(in Chinese)吴小霞,王明浩,明铭,等.大口径SiC轻量化主镜热变形得定标[J].光学 精密工程,2012,20(6):1243-1249.
[13] LIN X D,XUE C,LIU X Y Current Status and research development ofwave front correctors for adaptive telescope[J].Chinese Optics,2012,5(6):337 - 351.(in Chinese)林旭东,薛陈,刘欣悦,等.自适应光学波前矫正器技术发展现状[J].中国光学2012.5(6):337 -351.
[14] ZHAO H C,ZHANG JX,YANG Fetal.Preloading eight-van spider for supporting structure of secondary mirror[J].Opt.Precision Engineering,2013,21(5):1199 -1204.(in Chinese)赵宏超,张景旭,杨飞,等.预紧式八翼梁次镜支撑结构动力学分析[J].光学 精密工程,2013,21(5):1199-1204.
[15] Wolfgang Dierking.RMS slope of exponentially correlated surface roughnessfor radar applications[J].IEEE Transactions on Geoscience and remote sensing,2000,38(3):1451-1454.
[16] Ross Zhelem.Specificationof Optical Surface Accuracy U-sing the Structure Function[J].SPIE,2011,8083:808310-1~808310-10.
[17]Description of Free-form Optical Curved Surface Using Two_variable orthogonal Polynomials[J].Acta Optica Sinica,2012,32(9):092200201 - 092200210.(in Chinese)王庆丰,程德文,王涌天.双变量正交多项式描述光学自由曲面[J].光学学报,2012,32(9):0.9220021 -092200210.
[18] WANG Xu.Fabrication of SiCmirror in full aperture with optimized fixed abrasive polishing pad[J].Opt.Precision Engineering,2013,21(2):267 -273.(in Chinese)王旭.使用优化的固着磨料磨盘全口径加工碳化硅反射镜[J].光学 精密工程,2012,20(10):2123 -2131.
[19] CHENG JQ.Principles of astronomical telescope design[M].Beijing:China Science & Technology Press,2003.程景全.天文望远镜原理和设计[M].北京:中国科学技术出版社,2003.
