Regularization of Casimir free energy for p-dimensional Hypercubic Cavities inside D+1-dimensional Minkowski Spacetime

LIN Ruihui, ZHAI Xianghua

(Shanghai United Center for Astrophysics (SUCA),Shanghai Normal University,Shanghai 200234,China)

1 Introduction

The Casimir effect has given rise to many discussions in articles and books[1-7]for several decades.Yet it is still an active area,especially with the consideration of the temperature influence.In the work of Lifshitz and collaborators[9-10],they generalized Casimir′s result to the case of parallel dielectrics with the correction of temperature.Further study were done by Sauer[11],Mehra[12]and Brown and Maclay[13].The more complete theory was given by Schwinger et al.[14]some years later.In recent years,some controversies (See Ref.[15-17] and references therein.) attracted increasing interests in the study on temperature dependence of the Casimir effect and the progress is exciting in that there is a possibility to measure the thermal effect in the Casimir force[18].

The extraction of finite physical results from ill defined quantities has been well studied,and various methods such as the Green′s function method,the Abel-Plana formula and the zeta function technique,has been developed for the zero temperature Casimir effect,and generalized to the finite temperature case[19-22].The Casimir energy at finite temperature has also been calculated for more than four dimensional spacetime[1，23-24].Recently,Geyer et al.gave a critical discussion on the thermal Casimir effect in ideal metal rectangular boxes in three-dimensional space[25],where they used the zeta function technique to reproduce the standard result of the configuration of two perfectly conducting plates in three-dimensional space[2，5，7，13],pointing out a problem existed in some previous papers that the subtraction of the contribution of the black body radiation and other geometrical contributions of quantum origin were neglected,which led to the contradiction with the classical limit in high temperature regime.Geyer′s work[25]and some more recently works[26-28]arrived at a common recognition that the terms of order equal to or more than the square of the temperature should be subtracted but the reason was not stated clearly.

In this paper,the thermal Casimir effect for massless scalar fields inp-dimensional hypercubic cavity ofD+1-dimensional Minkowski space-time is considered systematically.After dividing the Casimir free energy into the zero temperature part and the temperature-dependent part,the zero point energy is obviously divergent for a restricted spatial volume so that there is no doubt on the regularization of it,while the temperature correction part is automatically finite and hence causes some misunderstanding in the literature about the regularization of it.In fact,only after both parts are regularized,the Casimir force tends physically to vanish with the size of the cavity increasing to infinity.Rigorous prove and derivation of the regularization on both parts are given in this paper using zeta function technique (for zero temperature part) and Abel-Plana formula (for temperature-dependent part).We find that the term to be removed for regularization of the temperature-dependent part in the case of periodic boundary conditions (BCs) is only the one corresponding to the blackbody radiation,but in the cases of Dirichlet and Neumann BCs,there are terms proportional to the power of the side length of the hypercube and the temperature to be removed.This result is general that the results of the cases of parallel plates and three-dimensional box in the literature could be included in.Furthermore,for all three kinds of BCs,we give the explicit expressions of the Casimir free energy in both low temperature (small separations) and high temperature (large separations) regimes,through which asymptotic behavior of the Casimir free energy changing with temperature and the side length is easy to see.The asymptotic behaviors of the thermal Casimir force as the side length going to infinity in different cases are also discussed.We use the natural units ħ=c=kB=1 in this paper.

The structure of the paper is as follows.In Sect.II the free energy is divided into zero temperature part and temperature-dependent part and the zero point energy is regularized using zeta function technique.In Sect.III we do the regularization of the temperature-dependent part using Abel-Plana formula and obtain the general results indicating the subtraction of the terms proportional to the powers of the side length to get the physical result.Sect.IV contains the results of the physical Casimir free energy in high temperature (large side length) regime.Sect.V includes the conclusions and discussion.

2 Regularization of the zero temperature part of the free energy

To deal with a quantum system at thermal equilibrium at temperatureT,the easiest and most frequently used method,which is known as the Wick′s rotation or Matsubara formalism,is to rotate the timet→-iτto obtain the partition function out of the path integral,confining the Euclidean timeτ∈[0,β],whereβ=1/T.Periodic BCφ(τ+β,x)=φ(τ,x) for bosonic field are imposed in the imaginary time coordinate.For massless bosonic field inD-dimensional space the partition function Z is then given by

(1)

(2)

In (D+1)-dimensional spacetime,for ap-dimensional hypercubic cavity with the sizeL,and with the sizes of the left (D-p)-dimensionLp+1,Lp+2,…,LD≫L,when the scalar field satisfies periodic,Dirichlet and Neumann BCs,after some standard calculation in quantum field theory,the Helmholtz free energies have the following expressions,respectively

(3)

(4)

(5)

where the superscripts (P),(D),(N) of F indicate the types of BCs.Thep-dimensional vectorsnin the summation signs denote the indexes (n1,n2,…,np),andn2will be used to denoten2=n12+n22+…+np2hereinafter.

One obvious observation is that the free energy is divergent and needs to be regularized.In the case of periodic BCs,utilize the formulae

(6)

and

(7)

the free energy density (energy per hyperarea) becomes

(8)

Carry out the integral overrusing the properties of Gamma function

(9)

(10)

whereu(s) is any regular function ats=0,one can get

(11)

Employ the Poisson summation formula

(12)

on the summation overn0,(11) becomes

(13)

where the free energy density is divided into two parts according tom0=0 or not in the last line.Since the first part can be re-obtain by takingβin eq.(11) to infinity and turning the summation overn0into an integral,it is just the zero temperature part of the free energy densityε0(P),while the other is the temperature-dependent partfT(P).

By using the integral forms of Gamma function eq.(9) and modified Bessel function of the second kindKν(z)

(14)

the two parts of the free energy density can be expressed as

(15)

and

(16)

It can be seen thatε0(P)is divergent,and hence it needs undoubtedly to be regularized.Using Epstein zeta function

(17)

and the reflection formula of it

(18)

the regularized (indicated with the superscript ″reg.″) convergent zero point energy density becomes

(19)

For the temperature-dependent part of the free energy density (16),it is automatically finite and thus the regularization of it was neglected in some previous papers.However,it is not difficult to find from eq.(16) that the free energy density as well as the Casimir force density are divergent whenLgoes large enough,which contradicts the fact that the Casimir force should tend to vanish with the increase of the separation.So the temperature-dependent part of the free energy density still needs to be regularized.

3 Regularization of the temperature-dependent part

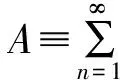
(20)

The regularizedAthen becomes

其次，政府相关部门要创造条件为集成电路企业在国内外的上市融资、开辟证券市场创业板等提供政策支持。针对市场前景乐观、人才优势明显的集成电路企业，在政府委托第三方评估部门的帮助下，经过充分的论证，可以突破一定比例的无形资产占净资产的比例 ，给集成电路企业以一定的股权自主权。此外，政府相关部门委派专门专业人才支持我国集成电路企业到境外上市，凡经专业部门审核符合境外上市资格的集成电路企业，允许到境外申请上市筹资，政府应出台相关的鼓励政策。

(21)

since according to eq.(20),the rest ofAis convergent in our cases.We will denote all terms related to the conjugate integral term in eq.(20) asCin the following without giving the explicit forms of them.

To use the Abel-Plana formula to regularize eq.(16),we start from defining

(22)

Then according to eq.(20),

(23)

Carry out the integral with (22) in advantage of eq.(6),then

(24)

So as eq.(21) indicates,the divergent part that needs to be subtracted fromfT(P)is

(25)

and then the regularized temperature-dependent part of the free energy density is

(26)

(27)

and

(28)

where the terms to be subtracted are

(29)

The "+" in all (±1)qs corresponds to Neumann BCs and "-" to Dirichlet ones,andn∈pin the summation sign is for Dirichlet whereasn∈(∪{0})pfor Neumann.

In the case ofD=p=3,from eqs.(25) and (29),for periodic BCs,the only term to be subtracted is

(30)

and for Dirichlet and Neumann BCs,the terms are

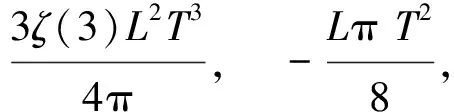
(31)

where the sign "-" corresponds to Neumann BCs and the sign "+" to Dirichlet BCs.It is obvious that theT4term that exists in all three cases is the blackbody radiation energy restricted in the volumeL3.And the three terms in (31) for Dirichlet BCs are exactly the results obtained in the previous papers[25,33-35].Therefore,(25) and (29) are the general results of the subtraction to get the physical Casimir free energy density forp-dimensional hypercube in (D+1)-dimensional spacetime.

We utilize the Abel-Plana formula to regularize the temperature-dependent part of the free energy density and re-obtain that the terms of order equal to or more than the square of the temperature,as stated in refs.[25-28],are to be subtracted.And as eqs.(25) and (29) indicate,these terms are proportional to the powers of the side length,and hence are exactly the terms that make the temperature-dependent part of the free energy divergent when the side length tends to infinity.

4 Alternative expressions of the Casimir free energy

(32)

(33)

It is easy to see that the last terms of each equation are the sources of divergency whenL→∞,and hence are to be removed for regularization reasons.Furthermore,one can find that these terms are exactly the eqs.(25) and (29),which are also related to the regularization in low temperature expansions.Therefore,we obtain the terms to be subtracted to get the finite physical results through two different ways.And the physical(indicated with the superscript ″phys.″) free energy densities in high temperature regime are expressed as

(34)

and

(35)

From these high temperature expressions (34) and (35),one can easily observe the asymptotic behaviors of them in high temperature or large separations limits.And more importantly,with the relation of the Casimir force densityFCas.to the physical free energy densityfPhys.

FCas.tends to vanish with the separationLgoing to infinity and tends to be proportional to temperatureTat high temperature.

5 Conclusions and discussion

We have reconsidered the thermal scalar Casimir effect forp-dimensional hypercubic cavity insideD+1-dimensional Minkowski spacetime.Our main conclusions are as follows:

(i) We provided a rigorous derivation of the regularization of the zero temperature part using zeta function technique and the temperature-dependent part using Abel-plana formula,and obtained a general result that could include the cases of parallel plates and three-dimensional box in the literature.

(ii) We give the explicit expressions of the Casimir free energy density in both low temperature (small separations) and high temperature (large separations) regimes,through which the asymptotic behavior of the free energy density changing with temperature and the side length is easy to see.

(iii) The Casimir free energy densities are convergent and the Casimir force densities indeed tend physically to zero as the separationL→∞ after both the zero temperature and the temperature-dependent parts of the free energy densities are regularized.

We hope we have provided a comprehensive and complete understanding to this old problem analytically.The case of a close cavity,i.e.D=p,which is a little different in that some terms will go divergent takingD→pin eqs.(34) and (35),will be discussed in the following study.The arguement that both the zero temperature and the temperature-dependent parts need to be regularized to get the physical Casimir free energy is true for any configurations other than hypercubic cavities when the temperature modification of the Casimir effect is considered.In addition,the other thermodynamical quantities such as the entropy can also be considered and the same problem for electromagnetic field is also worthy to study.

:

[1] BORDAG M,KLIMCHITSKAYA G L,MOHIDEEN U,et al.Advances in the Casimir Effect[M].Oxford: Oxford University Press,2009.

[2] BORDAG M,MOHIDEEN U,MOSTEPANENKO V M.New developments in the Casimir effect[J].Phys Rept,2001,353(1-3):1-205.

[3] PLUNIEN G,MÜLLER B,GREINER W.The Casimir effect[J].Phys Rept,1986,134(2-3):87-193.

[4] MILONNI P W.The Quantum Vacuum[M].San Diego: Academic Press,1994.

[5] MOSTEPANENKO V M,TRUNOV N N.The Casimir Effect and its Applications[M].Oxford: Clarendon,1997.

[6] KRECH M.The Casimir Effect in Critical Systems[M].Singapore: World Scientific,1994.

[7] MILTON K A.The Casimir Effect[M].Singapore: World Scientific,2001.

[8] SPARNAAY M J.Measurements of attractive forces between flat plates[J].Physica(Utrecht),1958,24(6-10):751-764.

[9] LIFSHITZ E M.The Theory of Molecular Attractive Forces between Solids[J].Soviet Phys JETP,1956,2(1):73-83.

[10] DZYALOSHINSKII I D,LIFSHITZ E M,PITAEVSKII L P.General theory of van der waals′ forces[J].Soviet Phys Usp,1961,4(2):153-176.

[11] SAUER F.Die Temperaturabhängigkeit von Dispersions-kräften[D].PhD Dissertation,Göttingen,1962.

[12] MEHRA J.Temperature correction to the casimir effect[J].Physica,1967,37(1):145-152.

[13] BROWN L S,MACLAY G J.Vacuum Stress between Conducting Plates: An Image Solution[J].Phys Rev,1969,184(5):1272-1279.

[14] SCHWINGER J,DERAAD JR L L,MILTON K A.Casimir effect in dielectrics[J].Ann Phys,1978,115(1):1-23.

[15] MILTON K A.The Casimir effect: recent controversies and progress[J].J Phys A,2004,37(38):R209-R277.

[16] BREVIK I,ELLINGSEN S A,MILTON K A.Thermal corrections to the Casimir effect[J].New J Phys,2006,8(10):236-255.

[17] MILTON K A.Recent developments in the Casimir effect[J].J Phys Conf Ser,2009,161(1):012001.

[18] GEYER B,KLIMCHITSKAYA G L,MOSTEPANENKO V M.Possibility of measuring thermal effects in the Casimir force[J].Phys Rev A,2010,82(3):032513.

[19] ELIZALDE E,ODINTSOV S D,ROMEO A,et al.Zeta regularization techniques with applications[M].River Edge,NJ: World Scientific Publishing Co Inc,1994.

[20] ELIZALDE E.Ten physical applications of spectral zeta functions[M].Berlin: Springer-Verlag,1995.

[21] KIRSTEN K.Spectral functions in mathematics and physics[M].Boca Raton,FL: Chapman and Hall/CRC,2002.

[22] KIRSTEN K.Casimir effect at finite temperature[J].J Phys A,1991,24(14):3281-3297.

[23] AMBJØRN J,WOLFRAM S.Properties of the Vacuum[J].Ann Physics,1983,147(1):1-56.

[24] LIM S C,TEO L P.Finite temperature Casimir energy in closed rectangular cavities: a rigorous derivation based on a zeta function technique[J].J Phys A,2007,40(38):11645-11674.

[25] GEYER B,KLIMCHITSKAYA G L,MOSTEPANENKO V M.Thermal Casimir effect in ideal metal rectangular boxes[J].Eur Phys J C,2008,57(4):823-834.

[26] BEZERRA V B,KLIMCHITSKAYA G L,MOSTEPANENKO V M,et al.Thermal Casimir effect in closed Friedmann universe revisited[J].Phys Rev D,2011,83(10):104042.

[27] TEO L P.Electromagnetic Casimir effect on the boundary of aD-dimensional cavity and the high temperature asymptotics[DB/OL].arXiv:1304.7557.http:∥arxiv.org,[2013-04-29].

[28] TEO L P.Finite temperature Casimir effect on spherical shells in (D+1)-dimensional spacetime and its high temperature limit[DB/OL].arXiv:1305.2240.http:∥arxiv.org,[2013-04-29].

[29] REVZEN M,OPHER R,OPHER M,et al.Casimir′s entropy[J].J Phys A,1997,30(22):7783.

[30] FEINBERG J,MANN A,REVZEN M.Casimir Effect: The Classical Limit[J].Ann Phys,2001,288(1):103-136.

[31] RUBIN S,FEINBERG J,MANN A,et al.Classical limit of the Casimir entropy for scalar massless field[J].Physica A,2007,384(2):335-345.

[32] CARUSO F,NETO N P,SVAITER B F,et al.Attractive or repulsive nature of Casimir force inD-dimensional Minkowski spacetime[J].Phys Rev D,1991,43(4):1300-1306.

[33] DOWKER J S,KENNEDY G.Finite temperature and boundary effects in static space-times[J].J Phys A,1978,11(5):895-920.

[34] VASSILEVICH D V.Heat kernel expansion: user′s manual[J].Phys Rept,2003,388(5-6):279-360.

[35] NESTERENKO V V,PIROZHENKO I G,DITTRICH J.Non-smoothness of the boundary and the relevant heat kernel coefficients[J].Class Quant Grav,2003,20(3):431-455.