基于不同模型的相对海平面变化分析

2014-03-20连丽珍王解先沈云中王卫安

海洋通报 2014年4期

连丽珍，王解先，沈云中，3，王卫安

（1.同济大学测绘与地理信息学院，上海 200092；2.现代工程测量国家测绘局重点实验室，上海 200092；3.同济大学空间信息科学及可持续发展应用中心，上海 200092）

海平面变化是全球共同关注的焦点之一，从20世纪中叶开始就有环境研究学者和测绘科学工作者利用验潮站资料研究海平面变化。在2000年前后，海平面变化速率的研究也逐渐的成为热点，涌现出大量数理分析方法，学者们利用这些方法更加科学和精确地计算了相对海平面变化的速率，并取得了一系列具有重要参考价值的结果。我国沿海地区人口相对集中、经济比较发达，是国家政治、经济、文化和社会发展的重要战略区域，但该地区地势低平，海拔一般只有2~5m，极易遭受海平面上升的影响。相对海平面上升对当地经济发展和人民生活均有直接影响，同时也对该区域的长期规划建设有重要影响。因而，研究该地区的相对海面变化尤其对沿海沉降地区更具有重要意义。

Emery（1980）以全球247个验潮站40年资料为基础分析得到了全球相对海平面变化率为3mm/a。Douglas（1997）对Douglas（1991）运用Tushingham等（1991）的冰后期回弹模型（PGR）进行修正，将所选的24个长期验潮站分为九个不同的地理区域，利用验潮站的观测资料得到全球平均1.8±0.1mm/a。Peltier（1999）开发了一个冰川均衡订正模型（GIA），并利用该模型得到20世纪全球海平面的总体上升速率为2.4mm/a。Barbosa等（2004）采用一种局部加权回归散点修匀法对大西洋东北区域的验潮站长期连续月均海平面资料进行非参数拟合和显著趋势分析，结果发现三个验潮站点处的海平面在1975年有一个明显的下降。Jevrejeva等（2006）提出了蒙特卡罗奇异谱分析（MC-SSA）方法求得1993-2000年数据得出全球海平面变化速率为2.4±1.0mm/a，并使用两种完全无关的方法（即，双边权鲁棒均值方差法和“虚拟站”法）估算了海平面序列中的误差项，结果发现，早期验潮站很少时，两方法估计的误差非常接近；当在20世纪中期验潮站数量较多时，双边权法所估误差明显小于“虚拟站”法所算的误差；此外还得出了“虚拟站”法比双边权法更可靠的结论。左军成等（1996）把最大熵谱分析、非线性最小二乘法应用于动态预报，得到太平洋海域海平面的平均上升速率为1.7mm/a。左军成等（1997）分析了太平洋海域48个长期验潮站数据，得出太平洋海域的月均海平面以平均速率1.7mm/a上升。夏华永等（1999）提出了一种带周期项的海平面变化灰色分析模型，并对广西海平面进行分析，得出了北海、涠洲、白龙尾3站的相对海平面上升速率依次为1.67mm/a、2.51mm/a、0.89mm/a。俞肇元等（2007）以吴淞站1955-2001年月平均潮位序列为基础，采用奇异谱分析（SSA）与自回归模型（AR）相结合的方案进行了月平均潮位预测试验，在其可对比预测的5年内，预测值与实测值的绝对误差平均值为2.83cm，预测值与实测值之间的均方差为4.51。俞肇元等（2008）以国内6个验潮站自20世纪50年代以来的月平均潮位序列为基础，采用奇异谱分析（SSA）与均值生成函数（MGF）模型相结合的方案，以各站位最初20余年数据为基础建立预测模型，以后续年份的实测数据进行了多方案对比验证及检验，结果发现各站位平均预测误差均不超过10cm，预测的绝对误差大部分落在±15cm之间，极端预测误差落在±30cm左右。。

为了比较不同方法的优劣和适用性，本文尝试多种方法和模型对14个验潮站多年海平面序列进行综合分析，进而提取月均海平面的趋势周期并建立整体模型以实现对未来海平面的预测。结果发现，采用不同分析方法所得到的结论并不完全一致，甚至同一个观测站数据采用不同方法得到的结果完全相反。

1 模型方法简述

相对海平面变化分析主要包括趋势估计和变化预测两部分，拟定采用3种模型，分析方法主要包括功率谱分析、最大熵谱分析、灰色模型、奇异谱分析、均生函数模型以及相关统计检验方法等，有关这些方法介绍详见本文所列的参考文献。本节主要针对趋势周期和海平面预测两方面的计算思路进行简要的介绍。

1.1 海平面变化趋势分析

在海平面验潮数据序列中，一般存在着趋势项、周期项等多种信息，还包含观测噪声，其趋势是最重要的关注点。趋势项的处理通常有简单线性趋势、带加速度的二次趋势和基于多项式逐步回归的非线性趋势三种形式，一般可表示如下

式（1）中：a0为待定的起始月的海平面，a1为待定的海平面的线性变化速率，a2为待定的海平面相对变化加速率，ai（i=3，4，…，10）分别为相应的非线性时间函数的系数。

由于周期提取情况将影响趋势分析结果的可靠性，因此关于谱分析确定序列中周期情况是不可忽视的。目前在周期选取方面先后出现了四种分析方法，即黄立人（1991）提出的t检验方法、李平等（2008）提出的功率谱分析方法、肖勃勃等（1983）和李平等（2008）先后都提出的最大熵谱分析方法、林继华等（1997）提出的显著周期分析方法。

除了以上三种趋势形式和四种周期谱方法的相互组合之外，还可以通过两种常用的方法求得趋势项：一种是通过构建灰色模型并求解参数，可得到站点瞬时线性变化速率和瞬时加速率；另一种是通过奇异谱分析提取序列中的趋势成分，进而对趋势成分进行线性拟合求解相对海平面线性变化速率，奇异谱分析确定主成分以后，对成分序列进行倾向性检验以提取趋势，进行周期性检验可以得到海平面变化的周期项。

1.2 未来海平面预测

综合采用三种方法预测未来海平面变化，即迭代趋势周期谱分析与ARMA结合（简称“传统分析模型”）；灰色模型与最大熵谱分析结合（简称“灰谱模型”）；奇异谱分析重构与均生函数结合（简称“重构均生模型”）。

传统分析模型通过迭代求解趋势和周期，直至所得残差序列满足ARMA建模的三个前提条件（平稳、正态和非独立性）为止，进而得到趋势周期残差ARMA的整体模型，实现海平面趋势的提取和未来海平面的预测。灰谱模型采用灰色建模与残差序列周期谱分析迭代求解周期项系数和灰色模型参数，直至残差序列中不存在周期为止，进而利用相关的周期灰色参数解进行未来海平面的预测。重构均生模型先对月均海平面序列进行奇异谱分析重构，以重构序列作为均生函数模型的输入因子，利用输入序列构建均生函数延拓序列，并将其视为周期性基函数，对这些因子进行正交化，最后利用双评分准则从中挑选出K个与原始序列关系密切的序列作为预报因子，建立多元回归模型进行预报。

2 基于中国近海验潮站数据的综合分析对比

利用Hawaii大学海平面数据中心提供的14个验潮站（站点分布见图1；其中，香港验潮站经纬度为（22°18′N，114°13′E））的多年逐时海平面数据进行相对海平面的分析和预测。有关各站点的数据起止时间见表1。由于各站点均存在不同程度上的缺失，本文首先采用逐年迭代调和分析进行数据补缺，进而利用陈宗镛（1960）提出的月均海平面计算方法得到各站点月均海平面序列。

图1 14 个验潮站点位置分布

表1 各站点数据长度

2.1 传统分析模型结果

是否进行预处理（主要包括多年移动平均和理论天文周期两种）、三种不同趋势形式（即简单线性、带二次加速度项和多项式逐步回归形式）和四种周期谱方法的不同组合（共计36种），分别对各站月均海平面序列进行分析。而在采用逐步回归确定趋势形式之后，对这个趋势项再进一步进行简单线性趋势拟合，进而得到站点相对变化速率。

由表2可以看出各站点相对变化基本呈线性，只有部分站点存在非线性变化。表2中t表示该站点处的相对海平面仅存在显著的线性变化速率特征，t2表示该站点处的相对海平面的线性变化速率也是变化的即存在加速率，log（t）表示该站点处的相对海平面存在对数变化的特征，e(-t)表示该站点处的相对海平面变化存在指数变化的特征。

表2 逐步回归时，各站点趋势项形式

以厦门站点为例，具体趋势和周期结果见表3。不同方法确定的周期存在其相同（如0.5a和1 a）和差异性。

表3 厦门站相对海平面变化分析结果

以厦门站为例，表4给出了由36种方法求得的该站上相对海平面序列的线性变化速率。表4中的方式1至方式4中所用的周期分析方式分别为T检验法、功率谱分析、最大熵谱分析和显著周期分析方法。

表4 36 种处理方式所得的厦门站点上相对海平面变化速率（mm/a）

图2给出36种组合方法所得各站点处海平面相对变化线性速率的变化范围。显然，不同方法所得的趋势变化存在微小差异，但其在大小和正负方向上是较为一致，即站点上不同方法所得的趋势倾向是较一致。结果表明，采用移动平均线性功率谱分析与移动平均线性显著周期分析方法在各个站点序列分析中所得结果均能通过显著性检验且计算效率较高。

采用迭代选择和剔除周期并解算其趋势周期系数，从而得到符合ARMA模型条件（平稳、正态和非独立）的残差序列，进而建立ARMA模型。通过残差序列建模之后，剩余的海平面值一般都在毫米级，且具有更强的随机性。采用了定阶后的ARMA模型和趋势周期成分一并进行建模，实现对未来海平面值的预测。在此以厦门40年作为建模分析数据，对其未来4年进行预测，具体结果见图3，拟合和预报的残差一般在±5cm之间。

图2 各方法所得各站点线性趋势速率分布图

图3 厦门月均海平面叠合模型回算及预测海平面图

此外，在计算中发现，使用不同的组合方法可能会出现不同异常的情况，甚至不同的趋势形式会导致所求的线性速率出现相反趋势。例如，对石臼所站点月均海平面序列进行逐步回归则无法确定趋势形式；采用二次趋势时：线性速率均为负且范围为-0.46~-7.78mm/a、加速率为正且范围为0.008~0.03mm/a2、周期主要包括（0.5a、1a、7.6a、8.9a、12a、15.3a、17.2a和22.9a）；简单线性趋势时：线性速率为正且范围为0.71~1.64mm/a、周期主要包括（0.5a、1a、8.1a、12.1a、17.2a和20.4a）。

2.2 灰谱模型结果

本文针对灰谱模型进行两方面的探讨，模型对月均海平面中的趋势和周期的提取能力；模型的预测能力。首先，根据周期谱分析与灰色模型迭代求解得到周期项，继而通过解得的参数a和u便可得到各站分析期间瞬时速率和加速率。计算结果表明，各站点的加速率（mm/a2）一般在10-9~10-10量级范围内，上升速率基本是在1~3mm/a范围内，具体周期和中间月份的线性速率结果见表5。其中，大连站点以速率-2.78mm/a下降，以加速率-3.08×10-8mm/a2减缓下降趋势，这与传统分析模型某些组合所得结果相反。

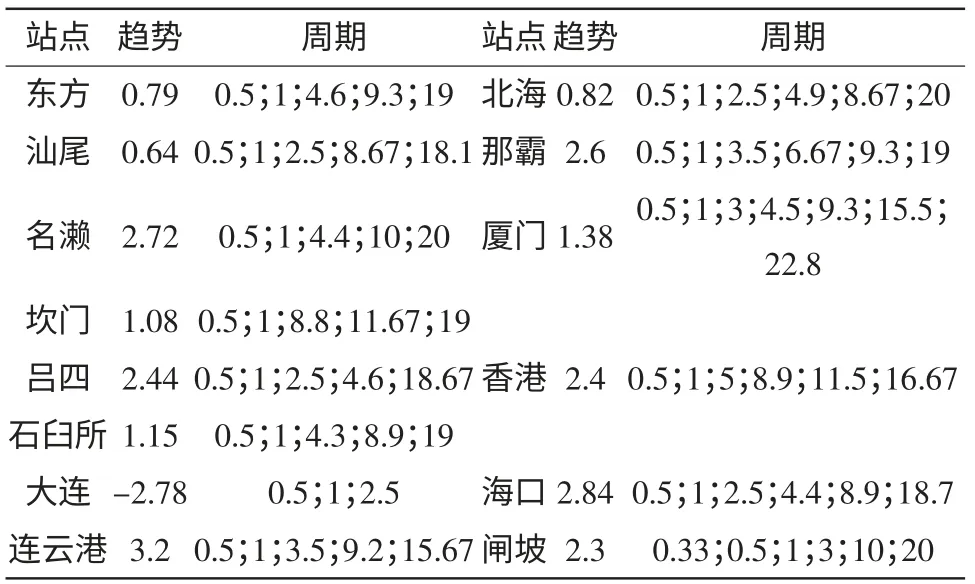
表5 各站点周期（a）和中间月份的趋势（mm·a-1）情况

根据所建立的带周期的灰色模型，对验潮站月均海平面序列进行了拟合和预测，下面仅给出北海、吕四、东方和海口四站的拟合预测图示（如图4）。

由图4可以看出，预测效果还是较好的。通过带周期项的灰色模型进行预测，其预测值与实际观测海平面的差值在±2dm，具体各站点预测均方误差及最大、最小误差如表6所示。

2.3 重构均生模型结果

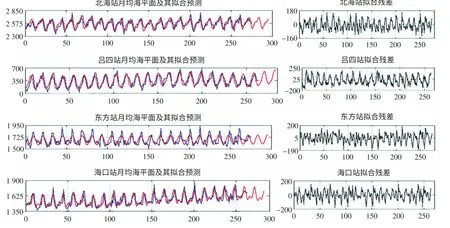
图4 各站点的月海平面拟合和预测情况（纵坐标：海平面（mm） ;横坐标：时间（月））

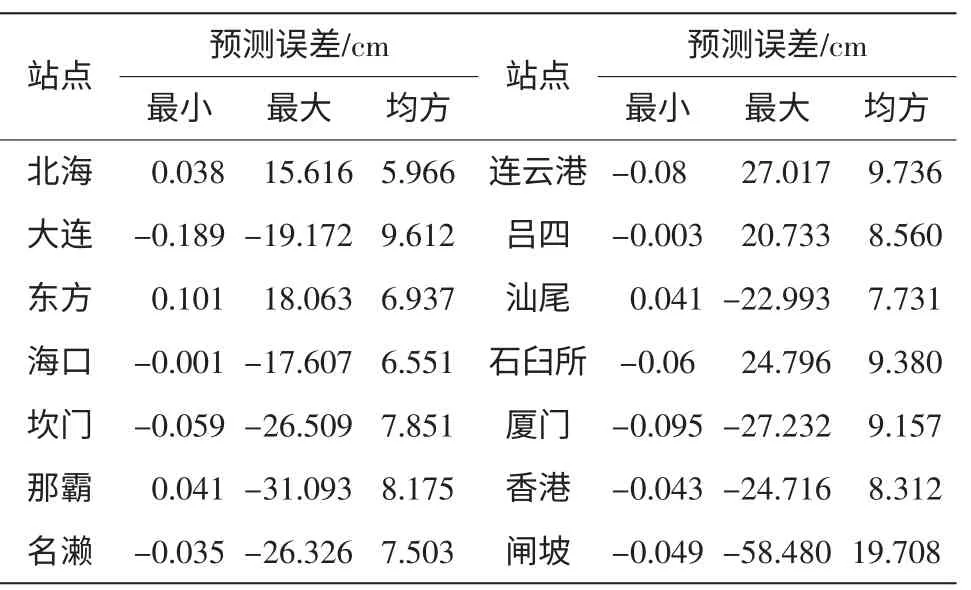
表6 各站点预测误差

对14个验潮站多年月均海平面序列进行奇异谱分析，得到了各站点的趋势成分和周期成分，在此基础上对趋势成分进行简单线性趋势拟合，获取站点的相对变化速率和起始月海平面值，如此可避免周期成分对趋势提取所造成的干扰。在奇异谱分析中，窗口和主成分的选取会影响趋势和周期成分的提取。鉴于奇异谱分析所得的周期范围小于其窗口长度，且奇异谱分析中须保证构造的滞后自协方差阵特征根的非负特性，本文主要是以“滞后自协方差阵的特征根非负”来确定最大窗口长度，并采用贡献率为85%确定主成分个数。结果表明，此取法是可行的。分析结果表明，各站点处海平面相对变化线性趋势一般在0.8mm/a至2.62mm/a范围内，略小于其他模型结果；而其提取出的周期一般也较短。各站点的趋势和周期具体结果如表7。

利用奇异谱分析重构降噪的特点，采用各站的重构海平面进行MGF建模，进而对未来月份的海平面值进行逐步预测和长期预测，具体结果见表8、图5和图6。

表7 奇异谱分析所得的各站点趋势和周期情况

由表8可以看出各站点的预测与实际之间的均方误差均在±1.5dm以内，最大差值也在3dm以内，其预测效果略优于其他两种模型。

由图5和图6也可以看出，利用重构均生函数进行未来海平面的逐步预测和长期预测，预测序列与实际海平面序列整体趋势和周期性较吻合，该预测是可行的。

3 结论

本文利用多种方法探讨了近海区域海平面的相对变化，并对各站点所处区域海平面进行建模预测。结果表明，我国近海各站基本以不同的速率在逐渐上升的，速率的范围是1mm/a~3mm/a，而不同分析方法所得的速率是不同的，甚至出现了相反的趋势（如大连站），这是由各种方法本身所具有的特点所限的。经过本文算例对比，重构均生模型既避免了趋势和周期之间的相互影响矛盾，其预测时又无需明确周期，且其趋势结果与公报结果一致，这也是该模型优于其他两模型的一大特点。此外，在海平面预测方面，三种模型的预测效果相差不大，基本都是在±2dm以内，而从预测长度上看，基于重构均生函数的长期预测效果要明显优于灰谱模型和传统分析模型，短期预测方面三者的预测效果较吻合。

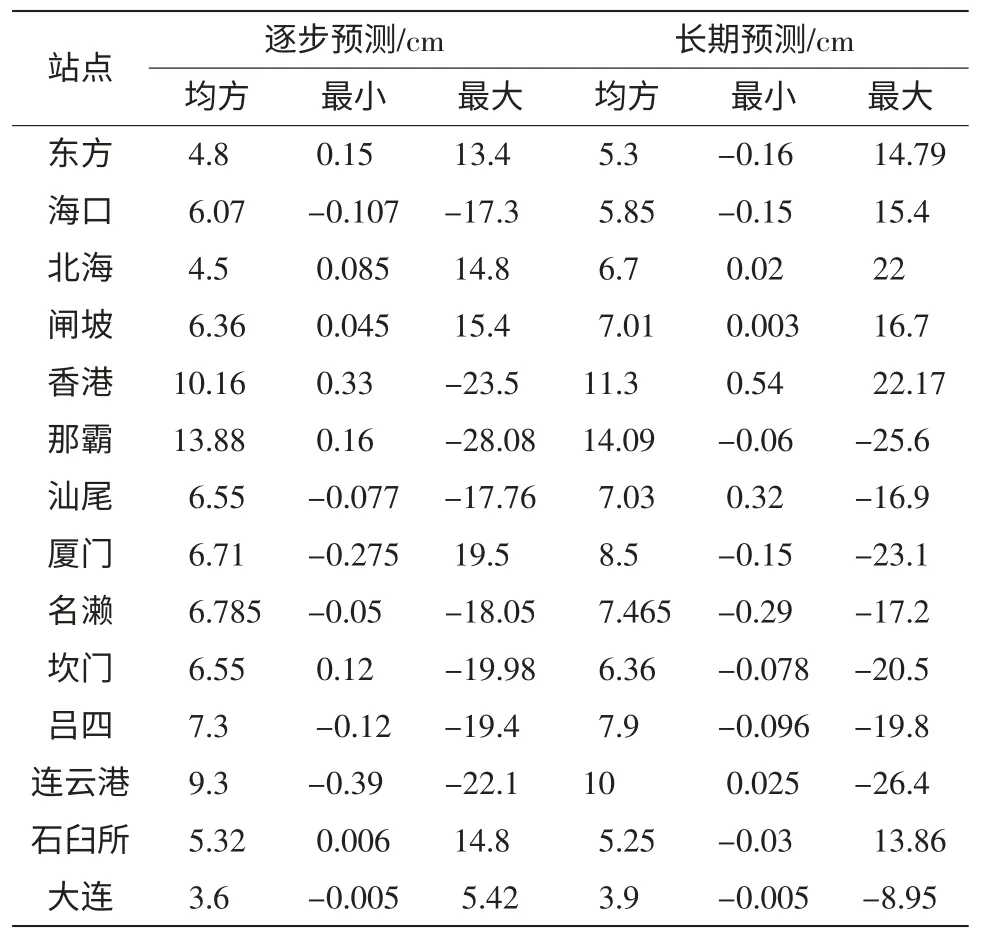
表8 各站点预测的均方误差和最大最小误差

图5 各站点实际海平面与基于SSA 重构的MGF 逐步预测海平面对比情况（纵坐标：海平面（mm） ;横坐标：时间（月））

各种方法所得的趋势结果，与海平面公报发布的数据较一致的，这个也是本文在判断各种模型是否可取的一个重要依据。通过不同方法对海平面相对变化研究是具有一定意义，根据结果可以在一定程度上对各方法模型进行不等权的取舍和综合，本文对此尚无给出相应的结论，这也是未来可以进一步研究的探讨点。

图6 各站点实际海平面与基于SSA 重构的MGF 长期预测海平面对比情况（纵坐标：海平面（mm） ;横坐标：时间（月））

Barbosa S M,Fernandes M J,Silva M E,2004.Nonlinear sea level trends from European tide gauge records. Annales Geophysicae, 22(5):1465-1472.

Douglas B C, 1991. Global sea level rise. Journal of Geophysical Research,96(C4): 6981-6992.

Douglas B C, 1997. Global sea rise：a redetermination. Surveys in Geophysics,18(2-3):279-292.

Emery K O, 1980. Relative sea levels from tide -gauge records.Proceedings of the National Academy of Sciences of the United States of America,77(2):6968-6972.

Jevrejeva S, Grinsted A, Moore J C, et al, 2006. Nonlinear trends and multiyear cycles in sea level records. Journal of Geophysical Research,111(C09012):1-11.

Peltier W R, 1999. Global sea level rise and glacial isostatic adjustment.Global and Planetary Change,20(2-3):93-123.

Tushingham A M,Peltier W R,1991.Ice-3G：a new global model of late Pleistocene de-glaciation based upon geophysical predictions of post -glacial relative sea level change. Journal of Geophysical Research,96(B3):4497-4523.

Yue J, Dong Y, Chen M C, et al, 2011. Sea level change and forecast in the future-climate of the past,today and the future.Marine Science Bulletin,13(2):33-49.

Yue J,Dong Y,Wu S Y, et al, 2012. Climate warming and sea level rise.Marine Science Bulletin,14(1):28-41.

韩小燕,潘晓东,马林芳,2011. 浙南沿岸海表面温度分布特征.海洋通报,30(6):619-623.

黄立人,1991.海面变化趋势的动态预测.海洋通报,10(1):1-5.

李芙蓉,焦梦梁,2012. 南海海表面温度年代际异常变化特征及其与PDO 的联系.海洋通报,31(4):384-390.

李平,卢文喜,辛欣,等,2008. 挠力河流域降水量序列的功率谱分析和最大熵谱分析.世界地质,17(1):64-67.

林继华,刘序俨,郭逢英,等,1997. 福建沿海的海面变化及其影响.地壳形变与地震,17(4):27-31.

王慧,范文静,李琰,等,2012. 渤黄海沿海2月份海平面异常偏高成因分析.海洋通报,31(3):255-261.

王慧,范文静,张建立,等,2011.中国沿海近31年冬季海平面变化特征.海洋通报,30(6):637-643.

夏华永,李树华,1999.带周期项的海平面变化灰色分析模型及广西海平面变化分析.海洋学报,21(2):9-16.

肖勃勃,孙祖宝,景芳盛,等,1983. 用最大熵谱分析方法提取周期信息.电子学报,11(5):88-92.

俞肇元,袁林旺,谢志仁,等,2007. 基于SSA 和AR 模型的海面变化预测试验.海洋湖沼通报,(4):14-19.

袁林旺,谢志仁,俞肇元,2008. 基于SSA 和MGF 的海面变化长期预测及对比.地理研究,27(2):305-311.