多馈入直流系统换流母线动态电压稳定性分析

，

(国核电力规划设计研究院，北京 100095)

0 引 言

直流输电系统运行中，换流器消耗的无功功率约占直流输送功率的40%～60%，而系统无功支撑不足正是其电压不稳定的主要原因，因此逆变侧的电压稳定问题尤为突出[1-5]。另外，直流输电系统的电压稳定还受所联交流系统的强度影响，交流系统强度在多馈入直流系统中体现为多馈入短路比。随着国内多条直流输电系统的陆续投产，迫切需要研究多馈入直流系统的动态电压稳定性。

文献[6]利用多馈入短路比指标分析了受端电网的强度，并讨论了直流系统落点位置对多馈入短路比的影响；文献[7]利用简化单馈入直流输电系统模型分析了直流输送功率极限与换流节点电压稳定性之间的关系；文献[8]以两馈入直流系统简化模型为基础，研究计及直流间相互作用后，多馈入直流系统运行状态变化、直流间耦合程度以及直流系统多馈入短路比大小对多馈入直流系统功率输送能力的影响。直流换流器运行时消耗大量无功功率，众多研究表明，在直流输电系统中稳定性问题最值得关注的是电压稳定问题[9-11]。相较于纯交流输电系统和单条直流输电系统，多馈入直流输电系统结构更为复杂，直流间复杂的相互作用对多馈入直流系统电压稳定影响较大[12-18]，多馈入直流系统的电压稳定性需要进一步深入研究。

基于以往直流输电系统的研究，建立两馈入直流输电系统简化模型，研究考虑直流间相互作用情况下，消耗无功大小、直流间耦合程度、以及多馈入短路比大小对多馈入直流系统电压稳定性的影响，并采用德国西门子公司开发的NETOMAC程序进行仿真。

1 两馈入直流系统简化模型

对多馈入直流系统相互作用机理的分析，采用图1所示的两馈入直流系统简化模型进行研究。模型中，交流系统采用戴维宁等效电路，即用一固定阻抗Z串联一固定电动势E串联来模拟。此模型对应于扰动发生后100～300 ms内交流系统特性，此时同步发电机的励磁调节器和交流系统的其它电压控制装置还未来得及响应。由于在逆变运行时，直流系统对交流系统强度的要求更高，因此假定模型中换流器均视为逆变器。

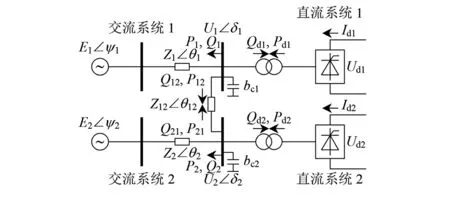
图1 两馈入直流系统简化模型

图1中，Ei∠ψi为交流系统等值电势；Zi∠θi为交流系统等值阻抗；Z12∠θ12为交流系统之间的耦合阻抗；Pi、Qi为交流系统有功和无功功率；Pdi、Qdi为直流系统有功和无功；Pij、Qij为交流系统之间的有功和无功交换；Ui∠δi为换流站交流母线电压；bci为交流滤波器和无功补偿电容的等值导纳；Udi、Idi为直流电压和电流，其中i、j=1,2，且i≠j。

2 多馈入短路比

交直流相互作用强度的大小，主要取决于交流系统短路容量相对于直流系统额定容量的强弱，即短路比指标。文献[11]给出了考虑多条直流相互作用和影响后，直流系统i的多馈入短路比(multi-infeed short circuit ratio，MSCR)为

(1)

式中，Ui为直流系统i换流母线电压；Zeqij为从各直流换流母线看进去的等值节点阻抗矩阵Zeq的第i行、第j列元素；Pdi、Pdj为直流系统i、j的直流功率。若以换流母线额定电压Ui为基准电压，则可得到

(2)

若考虑换流站换流母线侧的并联无功补偿设备的影响，则可推广定义多馈入有效短路比(multi- infeed effective short circuit ratio，MESCR)。

(3)

式中，Zci为直流系统i对应滤波器及无功补偿的阻 抗值。

以两馈入直流系统简化模型为例，如图1所示，等值节点阻抗Zeqij表达式为

(4)

(5)

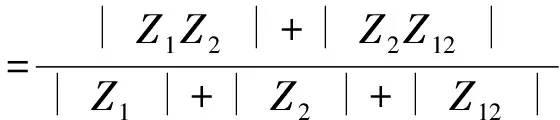
(6)

3 电压稳定分析

3.1 数学模型描述

针对图1所示的两馈入直流系统简化模型，可用以下11个方程来描述整个模型系统的特性。

Pdi=CiUi2[cos2γi-cos(2γi+2μi)]

(7)

Qdi=CiUi2[2μi+sin2γi-sin(2γi+2μi)]

(8)

Idi=KiUi[cosγi-cos(γi+μi)]

(9)

Udi=Pdi/Idi

(10)

Pi=[Ui2cosθi-EiUicos(δi+θi-ψi)]/|Zi|

(11)

Pij=[Ui2cosθij-UiUjcos(δi+θij-δj)]/|Zij|

(12)

Qi=[Ui2sinθi-EiUisin(δi+θi-ψi)]/|Zi|

(13)

Qij=[Ui2sinθij-UiUjsin(δi+θij-δj)]/|Zij|

(14)

Qci=bciUi2

(15)

Pdi=Pi+Pij

(16)

Qdi+Qi+Qij=Qci

(17)

式中，i、j=1，2，且i≠j；γi为熄弧角；μi为换向角；Ci和Ki为与换流变压器参数及与直流系统基准值有关的2个常数，其中Ci的表达式为

Ci=3STi/(4πPdNiuki%τi2)

(18)

式中，STi为换流变压器的容量；PdNi为直流系统额定容量；uki%为短路比；τi为变压器分接头。

在上述方程的变量中STi、uki%、Ci、Ki、bci、τi为换流站设备参数。|Z1|、θ1、|Z2|、θ2、|Z12|、θ12为受端系统参数。若在系统运行过程中，不改变变压器分接头和不投切补偿电容器，则可认为换流站设备参数是固定不变的。同样在系统运行方式确定后，受端系统参数也是固定的。交流系统采用戴维宁等效电路得到的等效电动势Ei也假定是固定的。这样上述方程中剩余的运行状态变量：γi、μi、Udi、Idi、Pdi、Qdi、Ui、δi、Pi、Pij、Qi、Qij、Qci(i，j=1,2，且i≠j)共有26个。而方程(7)～(17)在i,j=1,2且i≠j情况下共有22个约束方程。因此一旦确定26个状态变量中的任意4个变量，其余变量也就能被确定。

在图1所示的两馈入直流系统简化模型中，2条直流均工作在恒定熄弧角/恒定电流控制方式。在以下分析中，选取γ1、Id1、γ2、Id2为独立分量。首先假定换流站设备参数和受端系统参数，暂定STi=1.15PdNi，uki=0.18，τi=1，对应的Ci=1.53。取QcNi=QdNi=(0.5～0.6)PdNi，受端系统参数|Z1|=1/2，|Z2|=1/4，|Z12|=1，θ1=θ2=θ12=90°，则2条直流系统的多馈入有效短路比由式(3)计算为KMESCR1=1.84，KMESCR2=3.06。

模型系统在额定状况下运行时，有γi=γN=18°，Ui=1，Pdi=1，Idi=1。可由式(7)确定μNi，由式(9)确定常数Ki，又由式(8)、(15)确定bci，最后取E1∠ψ1为平衡节点，由式(16)、(17)确定交流系统等效电源参数。保持交流系统等效电源参数不变，对于给定的γ1、Id1、γ2、Id2，求解式(9)、(16)、(17)组成的非线性方程组，可以求出状态变量Ui、Uj、δi、δj、μi、μj，从而确定其余所有的运行状态变量。通过以上方法，可以画出在给定不同的γ1、Id1、γ2、Id2时，状态变量Qci随U1的变化曲线。

3.2 Q-U特性曲线分析

图1中直流系统1工作在恒定熄弧角控制方式时，直流系统2的电流不发生变化，且保持稳定运行。Qci减小时，U1随之减小，Qci减小到某一值时，潮流开始不收敛，因此存在该运行方式下的电压稳定临界点，即Q-U曲线最低点。

两馈入直流系统简化模型中直流系统1单独运行和与直流系统2形成多馈入运行2种情况的Q-U特性曲线如图2所示。图2中横坐标为直流系统1的换流母线电压，纵坐标为直流系统1换流母线注入的无功功率，单位均为标幺值。当系统运行在电压稳定临界点的左侧时，系统是不稳定的；当系统运行在电压稳定临界点的右侧时，系统是稳定的。由图2看出，直流系统1单独运行时，电压稳定临界点为U1=0.85。当与直流系统2相联形成多馈入运行后，直流系统1的电压稳定临界点为U1=0.8，位于直流系统1单独运行时的左侧。这说明与强交直流系统相联，能有效提高交直流系统换流母线电压稳定性。

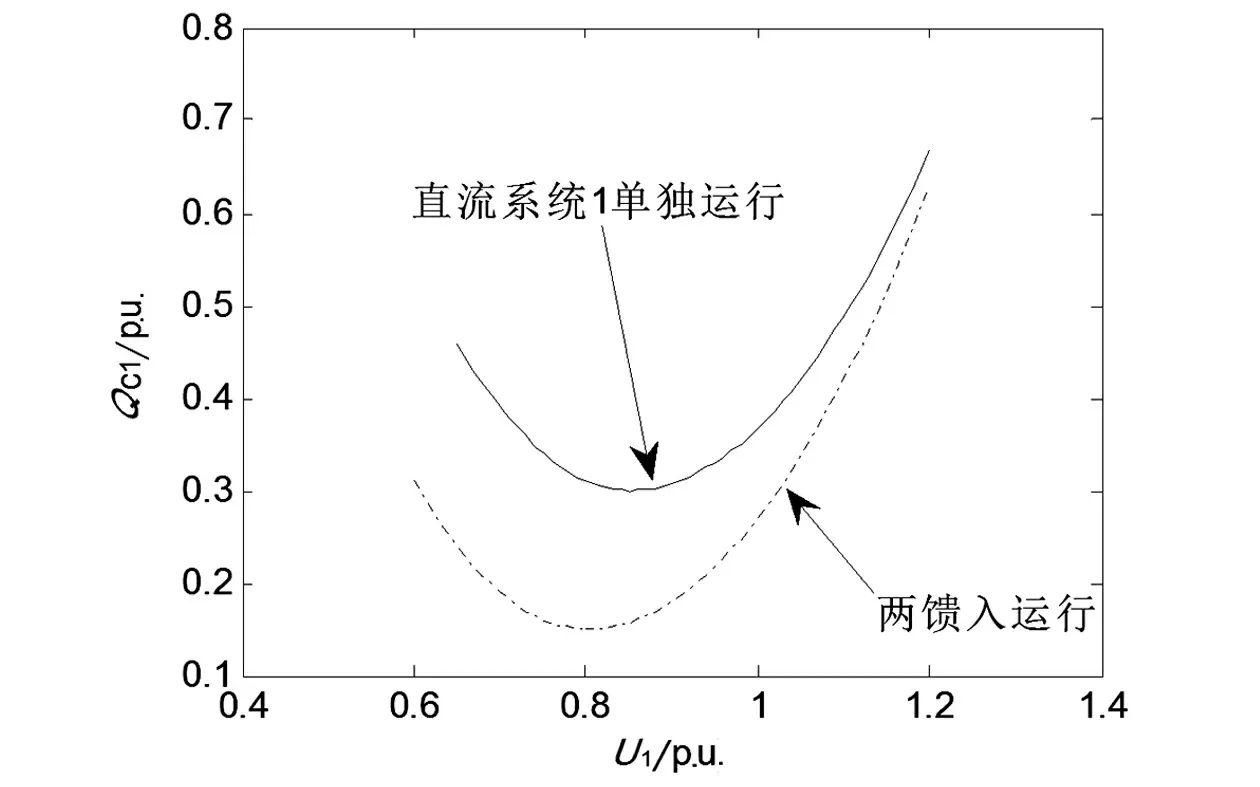
图2 单馈入与多馈入Q-U特性曲线

计及直流间相互作用后，任意直流系统运行状态变化都会对其他直流系统电压稳定性造成影响。让图1模型2条直流均工作在恒定熄弧角控制方式γ1=γ2=18°，设定Qc2为0.1～1.0 p.u.之间的任意常数，这样对应每一个Qc2都能画出一条Qc1随U1的变化曲线，如图3所示。

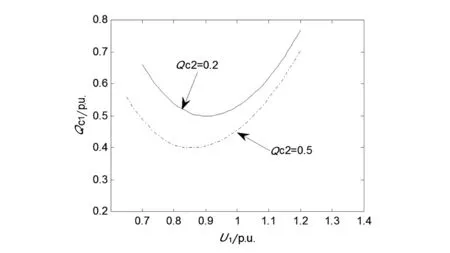
图3 不同Qc2的多馈入Q-U特性曲线

由3条曲线对比可看出，直流系统2换流母线注入的无功Qc2变化对直流系统1电压稳定性的影响，当直流系统2换流母线注入的无功越大，第1回直流的电压稳定裕度越大，所能达到的多馈入直流系统电压稳定裕度也越大。

在多馈入直流系统中，各直流系统之间通过联接在换流母线上的耦合阻抗Z12来相互作用。耦合阻抗Z12的大小，反映了直流系统1、2之间电气耦合的紧密程度。Z12越小，表明直流系统1、2之间电气距离越近，两个直流系统耦合程度越紧密。图4给出了当耦合阻抗Z12取不同值时，直流系统1的无功功率Qc1随U1的变化曲线。图4表明减小与强交直流系统之间的电气距离，能有效提高较弱直流系统电压稳定裕度，改善系统稳定性。

图4 不同Z12的多馈入Q-U特性曲线

在单条直流系统电压稳定分析中得到，直流系统短路比SCR越小，其电压稳定性越差。提高直流系统短路比，可以有效改善系统稳定性，提高电压稳定裕度。为考察两馈入直流系统简化模型中直流系统2短路比大小的变化对直流系统1电压稳定性的影响，设定直流系统2受端系统参数|Z2|分别为1/7、1/2。从而得到直流系统2多馈入有效短路比3.81、1.56。两种情况下，直流系统换流母线注入的无功功率Qc1随U1的变化曲线，如图5所示。

图5 不同KMESCR2的多馈入Q-U特性曲线

对比曲线得出，适当提高直流系统2的多馈入有效短路比大小，能有效提高直流系统1的电压稳定裕度。

4 结 论

(1)与强交直流系统相联形成多馈入直流系统，能有效增大较弱直流系统的电压稳定裕度，改善系统稳定性。

(2)在多馈入直流系统中，在一定范围内增大换流母线无功功率补偿、减小与强直流系统间电气距离、增大所联系统多馈入有效短路比均能有效增大直流系统的电压稳定裕度。

[1] Kunder P．Power system stability and control[M]．北京：中国电力出版社，2002：648-689．

[2] 李兴源．高压直流输电系统的运行和控制[M]．北京：科学出版社，1998：153-167．

[3] 赵畹君．高压直流输电工程技术[M]．北京：中国电力出版社，2004：10-25．

[4] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京:清华大学出版社, 2002.

[5] 周双喜, 朱凌志, 郭锡玖, 等.电力系统电压稳定性及其控制[M]. 北京: 中国电力出版社, 2004.

[6] 邵瑶，汤涌，郭小江，等．多直流馈入华东受端电网暂态电压稳定性分析[J]．电网技术，2011，35(12)：50-55．

[7] 邱革非，束洪春，董俊，等．联于弱交流系统的HVDC输电系统输电能力和电压稳定性的研究[J]．昆明理工大学学报：理工版，2005，30(3)：50-55．

[8] 陈虎，张英敏，贺洋，等．多馈入直流输电系统功率稳定性分析[J]．电网技术，2011，35(6)：50-54．

[9] 林伟芳，汤涌，卜广全．多馈入交直流系统电压稳定性研究[J]．电网技术，2008，32(11)：7-12．

[10] 邵瑶，汤涌．多馈入交直流混合电力系统研究综述[J]．电网技术，2009，33(17)：24-30．

[11] 林伟芳，汤涌，卜广全．多馈入交直流系统短路比的定义和应用[J]．中国电机工程学报，2008，28(31)：1-8．

[12] 邵瑶，汤涌．采用多馈入交互作用因子判断高压直流系统换相失败的方法[J]．电机工程学报，2012，32(4)：108-114．

[13] 蔡泽祥，朱浩骏，白雪峰，等．多馈入直流输电系统的动态特性及稳定控制与分析[J]．华北电力大学学报，2004，31(5)：1-8．

[14] 洪潮，饶宏．多馈入直流系统的量化分析指标及其应用[J]．南方电网技术，2008，2(4)：37-41．

[15] 吴冲，李兴源，何朝荣．多馈入直流交互作用因子在换相失败研究中的应用[J]．继电器，2007，35 (9)：26-31．

[16] 徐政.交直流电力系统动态行为分析[M].北京：机械工业出版社，2004:67-71.

[17] Denis L H A，AnderssonG．Voltage Stability Analysis of Multi-infeed HVDC Systems[J]．IEEE Transactions on Power Delivery，1997，12(3)：1318-1308．

[18] Paulo F D T，Bernt B，Gunnar A．Multiple Infeed Short CircuitRratio：Aspects Related to Multiple HVDC Into one AC Network[C]// Transmission and Distribution Conference & Exhibition：Asia and Pacific， Dalian，China：IEEE ，2005：1-6．