自然覆冰条件下的输电线路覆冰形状特征

，，，

(国网四川省电力公司电力科学研究院，四川 成都 610072)

0 引 言

输电线路覆冰易造成导线舞动、断线、倒杆(塔)、绝缘子闪络、线路跳闸、甚至使电网瘫痪等事故，严重威胁电力系统的安全运行，影响人们正常的生产和生活，从而造成巨大的经济损失和一定的社会影响[1-4]。2008年年初，中国南方也曾发生过大范围冰灾，致使至少7 541条10 kV以上的输电线路和859座35 kV以上变电站停运[5]。2012年年初，持续低温雨雪天气导致南方电网部分电力线路出现严重覆冰，贵州和广西电网共有超过20条500 kV输电线路出现闪络导致跳闸等覆冰事故。2013年12月底，四川省西昌市大箐梁子段输电线路发生严重覆冰，造成2条500 kV输电线路地线断线。2014年3月初，四川电网500 kV甘蜀一二线因覆冰在半小时内连续跳闸6次。

2008年的大范围冰灾过后，国家电网公司和中国南方电网都积极发展融冰技术，并开发了大量的直流融冰设备，在防止输电线路因覆冰断线、倒塔中发挥了重要作用。

在输电线路冰融之前，首先应正确估算融冰时间或融冰电流。目前几乎所有的估算方法都有一个共同的假设，即认为导线的覆冰形状具有一个圆形的横截面[6-8]。然而这种假设往往与大多数输电线路实际覆冰情况不符。文献[9]把导线覆冰后的横截面形状分成7种：圆形、椭圆形、扇形、梳子形、针形、盒形和波浪形。对于覆冰导线来说，圆形或椭圆形的横截面更为常见。如果利用圆形覆冰导线冰融时间的估算方法来计算非圆形覆冰导线的冰融时间，将会产生一定的偏差，在特殊情况下，甚至导致估算值完全不符实际。因此，分析导线覆冰的形状特征具有重要的意义。在众多现场试验调查的基础之上，提出了一个椭圆形的模型来描述覆冰导线的形状特征，并分析了不同覆冰形状对输电线路融冰时间的影响。

1 覆冰导线的形状特征

导线覆冰的截面形状与风速和风向、过冷却水滴的大小、导线的刚度等因素有关，其中导线的刚度起着决定性作用[10-13]。

图1 气液二相流碰撞导线的轨迹

如图1所示，当气流携带过冷却水滴绕过导线时，由于空气的粘滞性，气流在导线的迎风面被阻滞。而过冷却水滴的动量比气流的动量大，在导线的迎风面，过冷却水滴与气流分离后与导线发生碰撞，导致导线迎风面覆冰[9]。

图2 导线覆冰的过程

如图2所示，当迎风面的冰层达到一定厚度之后，冰层重力产生的力矩(M1)促使导线发生扭转，同时导线自身的刚度产生与冰层重力矩相反的抗扭转力矩(M2)[14]。当M1>M2时，覆冰导线将发生扭转，从而使导线的各个面均有覆冰；当M1≤M2时，导线不发生扭转，冰层只在导线的迎风侧增长。对于刚度比较小的导线，导线覆冰的截面形状更接近于圆形[15]，而对于刚度比较大的导线，其覆冰后的截面形状一般呈狭长的椭圆形状或其它不规则形状[16, 17]。对于不同的输电线路，档距较大的导线，刚度较小，覆冰导线的截面形状接近圆形；而对档距较小的导线，刚度较大，覆冰导线的截面形状接近于椭圆形或其它不规则形状。对于同一段输电线路，在距离塔(杆)较远处的导线，由于刚度较小，覆冰的截面形状更接近圆形；而接近塔(杆)部分的导线，由于刚度较大，覆冰的截面形状更接近椭圆形或其他不规则形状[15]。

根据观察的导线覆冰形状，通过其横截面轮廓，可以将冰导体划分成圆形、椭圆形、扇形、波浪状、梳状等。在自然覆冰站，已经发现，雨凇覆冰导线的横截面轮廓在大多数情况下是近似椭圆形的(如图3)，并且他们有共同的特点，即冰的最大厚度是在导线的迎风侧，而最小厚度在导线的背风侧。

图3 雨凇覆冰导线的截面形状(单位：mm)

图4 椭圆形覆冰导线

在图4中，把覆冰导线的横截面分为4个部分，即外界空气(θ0)、冰层(θ1)、导体的铝部分(θ3)和导体的钢芯(θ4)，且相邻区域之间的边界分别由Г01、Г13和 Г34表示。根据文献[10、16]的研究结果以及实验和实践的观测结果，提出以下两个假设。

(1)湿冰导线的横截面轮廓是圆形的或椭圆形的;

(2)冰的最大厚度在导线的上风侧，而最小厚度在导线的下风侧。

2 覆冰导线的数据模型

为了描述椭圆形覆冰的形状特征，定义两个无量纲数。

(1)

式中，ζ为覆冰偏心率，用来描述导线偏离冰层中心位置的程度；δ为覆冰扁度，用来描述覆冰导线的椭圆率；ai和bi分别表示椭圆形覆冰导线的短径和长径，m；dmin和dmax分别表示背风侧和迎风侧的覆冰厚度，m。当dmin=dmax时，ζ=0，表示导线的覆冰是均匀的；当dmin=0时，ζ=1，表示覆冰导线的背风面冰厚为零。当ai=bi时，δ=0，表示覆冰导线的截面形状为圆形。

为方便与圆形覆冰导线的比较，按照导线覆冰质量相等的原则把椭圆形覆冰导线等效成圆形覆冰导线，设圆形覆冰导线的等效覆冰半径为Req，其与bi、ai的关系为

(2)

式中，Req为椭圆形覆冰导线按覆冰质量相等的关系等效成圆形覆冰导线之后的等效半径，m。

根据式(1)和式(2)，ai、bi、dmin和dmax均可以用δ、ζ、Req表示为

(3)

(4)

式中，Rc为导线的半径，m。

根据假设(2)，导线围绕的冰层具有两个特点，如下。

(1)界面Г01的曲率总是大于界面Г13的曲率如图2所示，界面Г01和界面Г13可分别表示为

(5)

x2+y2=Rc

(6)

式(5)、式(6)对y的二阶导数为

(7)

(8)

根据假设(2)可知，界面Г01的曲率总是大于界面Г13的曲率，这就意味着当y为任意值时，式(7)的值总是大于式(8)的值，当y=0时，式(7)得到其最小值，因此

(9)

把式(1)和式(3)代入式(9)，则有

(10)

(2)覆冰厚度在背风侧最小

把式(6)写成极坐标形式为

(11)

式中，re为冰层外表椭圆的极坐标，m；rc为导线外表面圆的极坐标，m。

根据等式(11)，冰的厚度可表达为

di(θ)=re-rc

(12)

式中，di(θ)为冰层的厚度，m。

由图4可知，当θ=0时，di(θ) 获得其最小值(dmin) ，即

(13)

把式(1)和式(3)代入方程(13)，则有

(14)

根据δ和ζ的值，冰导线的横截面轮廓可分为3种类型(见表1)，即同心圆、偏心圆和偏心椭圆。无偏圆形覆冰是指覆冰的截面形状呈圆形，且与导线外表面圆同心的覆冰；偏心圆形覆冰是指覆冰的截面形状呈圆形，但不与导线外表面圆同心的覆冰；偏心椭圆形覆冰是指覆冰的截面形状呈椭圆形，且椭圆的中心不在导线外表面圆的圆心上。

在表1中，α和β分别表示为

表1ζ和δ取不同值时覆冰导线的形状

3 覆冰形状对融冰时间的影响

短路融冰电流计算公式为

(15)

ΔT=Ti-Ta

式中，rT为导线在温度T时刻的电阻率；Rc为导线半径；Ri为覆冰厚度；t为融冰时间，Ti为冰层温度；Ta为环境温度；va为环境风速。以LGJ-150导线为例，取覆冰厚度Ri为10 mm，冰层温度Ti为0 ℃，环境温度Ta为-5 ℃，环境风速va为5 m/s。

图5 覆冰偏心率对融冰时间的影响

由式(14)、(15)得出非均匀覆冰导线的融冰时间与导线覆冰偏心率的关系如图5所示。由图5可知，椭圆形覆冰导线偏心率对融冰时间有明显的影响。在其他融冰条件不变的情况下，偏心率越大，需要融化的冰层越薄，融冰时间越短。

当覆冰重量相同时，导线覆冰的偏心率ζ受扁度δ约束，当等效半径Req和扁度δ一定时，覆冰偏心率ζ有最小值。

(16)

覆冰偏心率的最小值与覆冰扁度的关系如图6所示。由图6可知，随着覆冰扁度的增加，覆冰偏心率的最小值也随着增加，即当覆冰导线越扁，导线偏心冰层的中心位置也越严重。

图6 覆冰偏心率的最小值(ζmin)与覆冰扁度(δ)的关系

由图7可知，由于覆冰扁度影响到覆冰偏心率的最小值，当导线上的覆冰重量相同时，即Req不变时，在覆冰偏心率取最小值时所对应的最大融冰时间随覆冰扁度的增加而减小，即覆冰形状越扁，最大融冰时间越小。

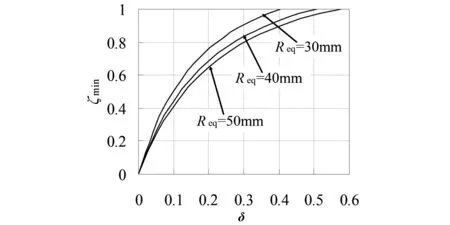
图7 覆冰偏心率的最小值(ζmin)与覆冰扁度(δ)的关系

4 结 论

在众多现场试验调查的基础之上，提出了一种椭圆形模型来描述覆冰导线的形状特征，并分析了不同覆冰形状对短路电流法融冰时间的影响，得出以下结论。

(1)现场实验结果表明，覆冰导线的横截面形状特征可以由椭圆模型来描述;

(2)根据覆冰导线的形状特征，覆冰导线的横截面形状可分为同心圆、偏心圆和偏心椭圆；

(3)椭圆形覆冰导线偏心率对融冰时间有明显的影响，在其他融冰条件不变的情况下，偏心率越大，需要融化的冰层越薄，融冰时间越短；

(4)随着覆冰扁度的增加，覆冰偏心率的最小值也随着增加，即当覆冰导线越扁，导线偏心冰层的中心位置也越严重；

(5)在覆冰偏心率取最小值时所对应的最大融冰时间随覆冰扁度的增加而减小，即覆冰形状越扁，最大融冰时间越小。

[1] 孙才新, 司马文霞, 苏立春. 大气环境与电气外绝缘[M]. 北京: 中国电力出版社, 2002.

[2] 蒋兴良. 输电线路导线覆冰机理和三峡地区覆冰规律及影响因素研究[D]. 重庆：重庆大学, 1997.

[3] 张宏志. 大面积导线覆冰舞动事故的调查与分析[J]. 东北电力技术， 2001(12): 15-19.

[4] 逸梅, 史惠萍. 绝缘子的覆冰及覆冰绝缘子的放电特性[J]. 广西电力技术, 1995(3): 20-24.

[5] 许树楷, 赵杰.电网冰灾案例及抗冰融冰技术综述[J]. 南方电网技术, 2008(2):1-6.

[6] Z. Péter: Modeling and Simulation of the Ice Melting Process on a Current- Carrying Conductor[D]. Quebec University，2006.

[7] J. Xingliang, F. Songhai, Z. Zhijin, S. Caixin, and S. Lichun: Simulation and Experimental Investigation of DC Ice-Melting Process on an Iced Conductor[J]. IEEE Transactions on Power Delivery, 2010(25): 919-929.

[8] 李和云. 过热导体的积冰和除冰机制[D]. 武汉：华中科技大学，2001.

[9] 蒋兴良, 杨辉. 输电线路的覆冰及防护[M].北京：中国电力出版社，2001.

[10] P. L. I. Skelton and G. Poots. Snow Accretion on Overhead Line Conductors of Finite Torsional Stiffness[J]. Cold Regions Science and Technology, 1991(19):301-316.

[11] G. Poots and P. L. I. Skelton. Simulation of Wet-snow Accretion by Axial Growth on a Transmission Line Conductor[J]. Applied Mathematical Modeling, 1995(19):514-518.

[12] 梁文政. 架空电力线路抗冰(雪)害的设计与对策[J]. 电力设备，2008(9):19-22.

[13] G. Poots and P. L. I. Skelton. Thermodynamic Models of wet-snow Accretion:Axial Growth and Liquid Water Content on a Fixed Conductor[J]. Lnternational Journal of Heat and Fluid Flow. 1995(16):43-49.

[14] 顾明, 马文勇, 全涌,等. 两种典型覆冰导线气动力特性及稳定性分析[J]. 同济大学学报：自然科学版，2009(37):1328-1332.

[15] M. Farzaneh, Atmospheric Icing of Power Networks[M]. New York: Springer, 2008.

[16] G. Poots and P. L. I. Skelton. The Effect of Aerodynamic torque on the Rotation of an Overhead Line Conductor During Snow Accretion[J]. Atmospheric Research，1995(36): 251-260.

[17] L. Makkonen. Estimation of Wet Snow Accretion on Structures[J]. Cold Regions Science and Technology，1989(17):83-88.