q元码距离分布的MacWilliams变换

高 云， 常星星， 肖 凌

(山东理工大学 理学院， 山东 淄博 255091)

近十年来，码的各种距离分布[1-3]及重量分布成为编码理论的研究热点之一. 码的距离分布能确定各种译码程序(如极大似然译码，误差检测等)的译码误差的概率，可以反映码的一些结构性质，并且能判断一些给定参数的码是否存在.1997年，万哲先[4]给出二元码距离分布的MacWilliams变换.2013年Huffman在文献[5]中给出扩域Fqt上的Fq-线性码的迹内积，对偶码，重量计数器，完全重量计数器，MacWilliams等式及Gleason多项式等问题.但目前还没有看到有关q元码距离分布的MacWilliams变换的研究.本文将[4]中二元码距离分布的MacWilliams变换理论推广到任意q元码.本文章列出Krawtchouk多项式的定义和部分性质，利用p次本原单位根给出Krawtchouk多项式值Kk(i)的另一种表达式，再利用此表达式给出q元码C的距离分布和重量分布的刻画.

1 预备知识

设n为固定的正整数，q为一素数方幂，x为不定元，则

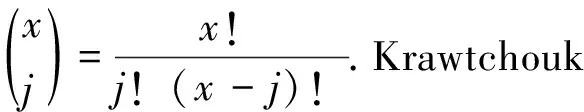
例1由Krawtchouk多项式的定义及三项递推式得：K0(x)=1,

K1(x)=nq-n-qx,

2 q元码距离分布的MacWilliams变换

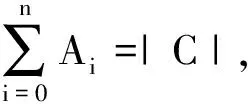
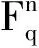
(1)

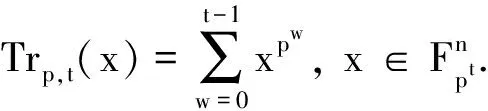
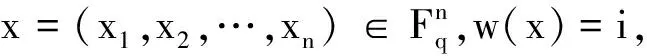
其中

并且

依此类推，得到

利用Kk(i)的上述表达式，可得到q元码C距离分布的MacWilliams变换的性质.

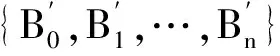
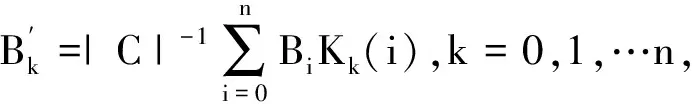
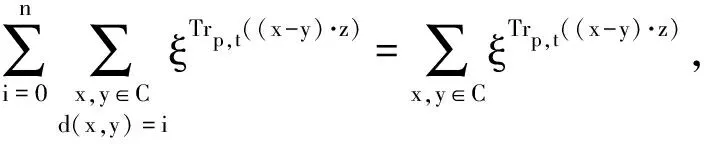
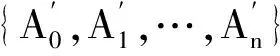
[1] Barg A, McGregor A. Distance distribution of binary codes and the error probability of decoding[J]. IEEE Trans Inform Theory, 2005, 51: 4 237-4 246.

[2] Ashikhmin A, Barg A, Litsyn S. Estimates of the distance distribution of codes and designs[J]. IEEE Trans Inform Theory, 2001, 47: 1 050-1 061.

[3] Ashikhmin A, Barg A. Binomial moments of the distance distribution: Bounds and applications[J]. IEEE Trans Inform Theory, 1999, 45: 438-452.

[4] Wan Z X. Quaternary codes[M]. Singapore: World Scientific Publishing Co Pte Ltd, 1997: 26-29.

[5] Huffman W C. On the theory ofFq-linearFqt-codes[J].Adv Math Commun, 2013,7(3): 349-378.