虚边界元法在二维涂层结构温度场中的应用

王发杰， 张耀明

(山东理工大学 理学院， 山东 淄博 255091)

近年来，随着表面技术及工程的发展，各种功能涂层由于其具有众多良好的性能而愈来愈引起人们的重视，应用范围涉及能源、石油化工、建筑、机械、航空航天等诸多领域，与国家经济建设、国防及人们的日常生活关系日益紧密，已成为表面工程技术的一个重要组成部分[1].然而，涂层材料厚度一般较薄，约在微米级甚至纳米级，受其厚度尺寸的限制，涂层材料中物理量的数值分析一直是工程中的难点.对这类结构采用有限元分析，受结构形状制约，为保证单元不退化，其长宽比必须协调，故所需划分的单元数量过大[2].边界元法可有效地处理涂层结构问题[3-5]，但涉及奇异边界积分和几乎奇异边界积分的计算麻烦，边界元法的精确度取决于这些奇异积分的计算效果，因此具有一定的难度而且耗时.

与传统边界元法相比，虚边界元法(Virtual boundary element method, VBEM)是一种无奇异边界元法[6]，其基本原理是通过真实边界外虚拟分布的源对场点的影响叠加产生一个位势积分，然后利用实边界条件，建立虚边界积分方程.虚边界元法避免了奇异积分的麻烦处理，消除了传统边界元法的边界层效应，具有程序设计简单，精度高，耗时短等优点，已广泛应用于各种常规结构，并取得了很好的效果[7-9].但是用于涂层结构的研究至今尚未发现.本文将虚边界元法应用于二维涂层结构温度场问题.由于虚边界分布在物理区域外，所以对于涂层问题的虚边界元法来说，一个区域的虚边界可能划分在另外一个区域.对此，本文利用复杂的多域技术(MDT)，发展了多域虚边界元法(MD-VBEM)，有效地计算了涂层问题.从而为涂层结构的研究开辟了新的途径，同时也拓展了虚边界元法的应用领域，即使涂层结构的狭长比小到1E-10，依然可获得非常高精度的数值解，而且方法程序设计简单，效率较高.

1 二维薄体结构位势问题的虚边界元法

假定 Ω是R2中的一个有界区域，Γ=∂Ω是边界.n=(n1,n2)是区域Ω的边界Γ在x点处的单位外法向量.

1.1 位势问题的控制微分方程

二维位势问题的控制微分方程为

边界条件为

式中u为势函数；n为边界外法线；Γu、Γq分别是u和∂u/∂n已知的边界.

二维位势问题控制方程的基本解为

1.2 二维位势问题虚边界元法的积分方程

设想假定Ω被嵌入一个无限的区域中，在Γ外的无限区域中有一延拓边界Γ′(这里称为虚边界)，沿着边界Γ′有一个待定的虚拟密度函数Φ(y)，令此虚拟密度函数对真实边界所产生的位势或法向梯度与边界条件一致，从而达到求解待定密度的目的.以上称之为虚边界元法.

位势问题中的虚边界积分方程为

(1)

(2)

计算内点位势和位势梯度的边界积分方程表示为

(3)

i=1,2,x∈Ω

(4)

1.3 二维涂层结构温度场问题的虚边界元法

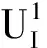
图1 分域法结构图

对于虚边界元法，在Ω1上可建立如下矩阵方程

(5)

同理，在Ω2上可建立如下矩阵方程

(6)

对于适定的边值问题，或者边界上的温度已知或者温度梯度已知.边界离散化后，每个节点上都会产生一个代数方程，方程的个数与虚边界节点处待求密度函数的个数相同，因而可以数值求解.分域法将区域Ω1与Ω2看成两个独立的问题来处理，在各自区域上利用虚边界元法进行计算，但在Ω1与Ω2的共同边界ΓI上，温度与温度梯度都是未知的，因此未知参量的个数此时大于代数方程的个数.要使得边值问题可解，必须引入边界ΓI上的温度和热通量协调条件：

(7)

假设边界Γ1，Γ2上节点的位势已知，根据条件式(7)、式(5)和式(6)可合并成

(8)

式(8)即为涂层结构温度场虚边界元法的基本列式.通过式(8)，可求出Ω1与Ω2虚边界上的节点密度函数，进而可以利用内点积分方程求出内点的物理参量.类似地，可写出其它边界条件下相应的方程组.

显然，以上过程可以直接推广到多涂层结构问题，只是联立方程的个数有所增加，这里就不再过多阐述.

2 数值算例

利用两个涂层问题的数值算例，来验证本文方法的有效性，所有算例均采用常单元等额配点法.为了表明方法数值解的准确性，定义如下平均相对误差

(9)

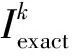
虚边界元法的求解精度受虚实边界间的距离影响.以下算例中，选择近、中、远三种不同的虚实边界间的距离[10]，对不同狭长比的涂层问题进行计算，都获得了令人满意的数值结果，表明虚实边界间的有效距离选取范围非常宽泛.

例1 圆环涂层结构的热流问题.基体Ω1内径为r1=10m，外径为r2=11m；涂层Ω2外径为r3，如图2(a)所示.已知基体内表面温度为10℃，涂层外表面温度为20℃.基体导热率为k1=1，涂层的导热率为k2=2.定义薄体区域特征值最小尺寸与最大尺寸之比δ=(r3-r2)/r1为狭长比.

根据热传导理论，涂层与基体温度的解析解分别为

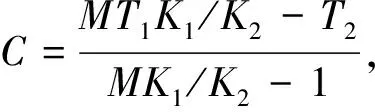
(a) (b) (c)图2 涂层结构圆环区域的热流

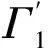
单元划分情况不变，狭长比为δ=10-10，虚实边界距离取中等距离组d1=5,d2=10.图5和图6分别列出了不同狭长比下，界面点 B(r2,0)上温度和热流的计算结果.可以看出数值解与精确解十分地接近.此算例充分体现了本文方法在计算涂层结构问题时的可靠性和精确度.

图3 界面温度解的平均相对误差

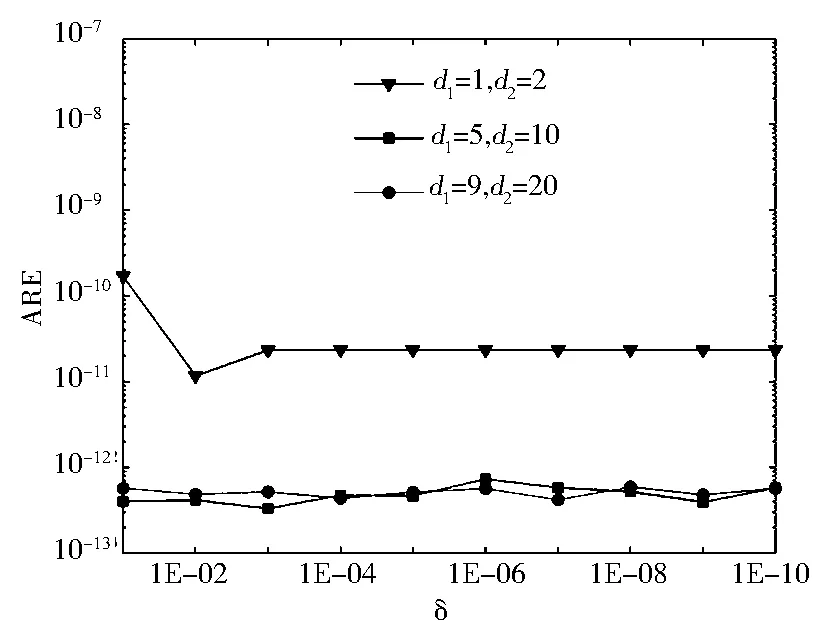
图4 涂层外表面热流解的平均相对误差

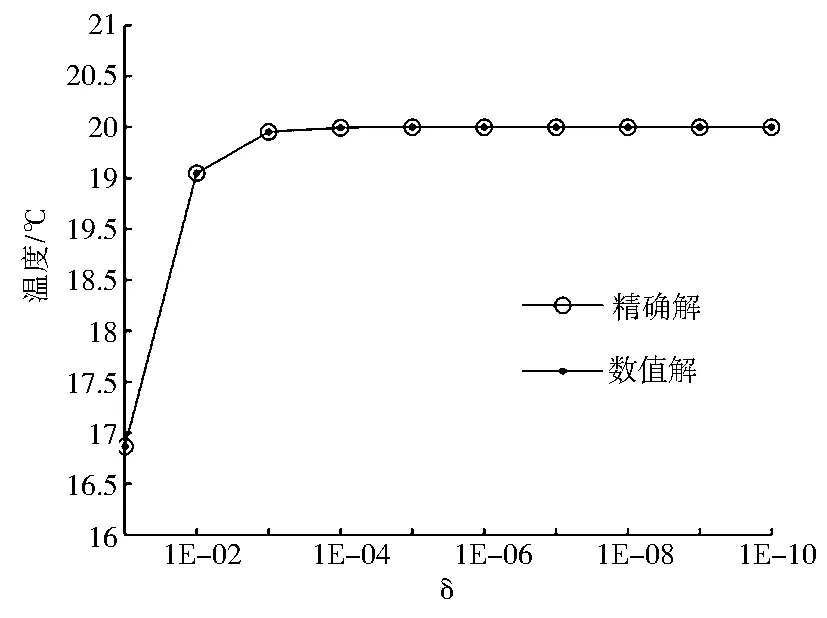
图5 界面点B处的温度

图6 界面点B处的热流

例2 矩形涂层结构的热流问题.涂层的厚度为h，基体的厚度为H=1m，宽度为 L=2m，涂层与基体的导热率分别为 k1=1，k2=2，边界条件如图7(a)所示.

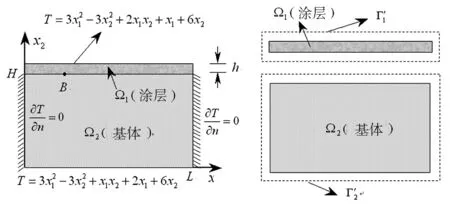
(a) (b)图7 涂层结构矩形区域的热流

采用MD-VBEM，图7(b)给出了基体和涂层结构及虚边界计算模型.在这里将基体和涂层的虚、实边界距离取为相同的值d.基体虚边界四边各划分为10个单元，涂层上下虚边界各划分为10个单元，左右两边各划分为2个单元，总共64个单元.当涂层厚度h从10-1m到10-10m之间变化时，分别取近中远三种不同的虚实边界距离，计算界面上配点处的温度以及涂层上表面配点处的热流.图8及图9给出了数值解的平均相对误差随涂层厚度变化的曲线.从图8和图9中可以看出，当涂层厚度h从10-1m到10-10m变化时，中等距离d=10和较远距离组d=20时的数值解相对误差非常小；较小距离d=0.5时的数值解的精度稍差，但仍然具有较高精度.表明，虽然虚实边界间的距离选取对解的精度有影响，但是有效距离的选取范围任然相当地宽泛.

图8 界面温度解的平均相对误差

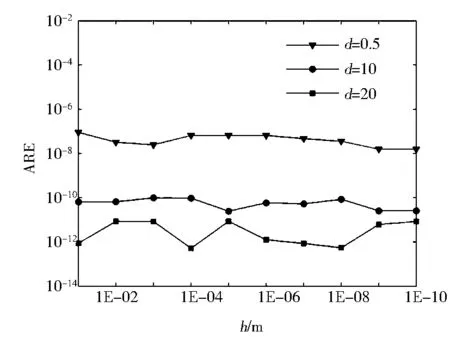
图9 涂层上表面热流解的平均相对误差

单元划分情况不变，涂层厚度为h=1.0E-10m，虚实边界距离取中等距离d=10.图10、图11分别给出了界面点B(0.5,1)处热流和温度梯度 ∂u/∂x1的计算结果.从图10、图11中可以看出，所得数值解与精确解十分吻合，并不受涂层厚度变化的影响，即使涂层厚度h达到1.0E-10m，本文方法任然可以得到可靠、稳定的数值解.

图10 界面点B(0.5,1)处的热流

图11 界面点 B(0.5,1)处的温度梯度

3 结束语

本文将虚边界元法应用于二维涂层结构温度场问题，提出了多域虚边界元法，成功求解了二维涂层结构问题.从而给出了求解二维涂层结构温度场问题的新途径，同时也拓展了虚边界元法的应用范围.数值算例表明，虚实边界距离的选取相当宽泛，即使涂层结构的狭长比小到10-10，依然可获得高精度的数值解.

[1] 胡传炘. 特种功能涂层[M].北京: 北京工业大学出版社, 2009.

[2] Luo J F, Liu Y J, Berger E J. Analysis of two-dimensional thin structures (from micro- to nano-scales) using the boundary element method[J].Computational Mechanics, 1998, 22:404-412.

[3] Du F, Lovell M R, Wu T W. Boundary element method analysis of temperature fields in coated cutting tools[J]．International Journal of Solids and Structures, 2001, 38:4 557-4 570.

[4] 程长征,牛忠荣,周焕林,等.涂层结构中温度场的边界元分析[J].合肥工业大学学报, 2006, 29(3): 326-329.

[5] 张耀明,谷岩.涂层结构中温度场的边界元解[J].固体力学学报, 2011，32(2)：133-141.

[6] 孙焕纯，许强. 无奇异边界元法[M].大连:大连理工大学出版社, 1999.

[7] Yao W A, Wang H, Virtual boundary element method for 2-D piezpelectric media[J]. Finite Elements Anal Des,2005,41:875-891.

[8] Li X C, Yao W A.Virtual boundary element-integral collocation method for the plane magnetoelectroelastic solids Engineering[J]. Analysis with Boundary Elements,2006,30:709-717.

[9] Yang D S, Xu Q, Virtual boundary meshless least square integral method with moving least squares approximation for 2D elastic problem[J]. Engineering Analysis with Boundary Elements 2013,37:616-623.

[10] 张耀明,孙焕纯,杨家新.虚边界元法的理论分析[J].计算力学学报, 2000, 17(1): 56-62.