氢负离子在非均匀电场中的光剥离

田金承 ， 王一豪，傅佃亮

(1.山东铝业职业学院 电气工程系， 山东 淄博 255065；2.鲁东大学 物理与光电工程学院， 山东 烟台 264025)

在过去的20多年间，氢负离子在外电场中的光剥离已经被广泛研究.氢负离子在非均匀电场中的光剥离截面的开创性的工作也被Bryantet[1]等人完成.根据他们的研究表明，光剥离截面会呈现出一个波浪结构，这可认为是在一个光滑的背景上额外的加上一个正弦振荡.此外，氢负离子在其它的场中，例如：电场和磁场相互平行的场中[2-3]，电场和磁场正交的场中[4-6]，以及任意方向的电场和磁场[7-9]等情况，都已经被一些理论工作者研究过了.近些年来，随着表面物理的发展，在临近物质表面情况下，氢负离子在外电场中的光剥离[10-16]成为研究热点.此前的研究中，涉及到的都是均匀电场和均匀磁场中的光剥离，但是非均匀外场中氢负离子的光剥离却很少被人研究.

1999年杨光参和杜孟利首次研究了梯度电场中的氢负离子光剥离[17].研究表明氢负离子在均匀电场中的光剥离截面会呈现出一个不对称的锯齿状结构.有关非均匀电场和非均匀磁场中氢负离子的光剥离的研究较少.本文利用了杜孟利和Delos提出的闭合轨道理论[18]，首次研究了氢负离子在非均匀电场中的光剥离.非均匀电场可以通过改变电场的方向和大小来获得.通过与均匀电场中氢负离子的光剥离截面对比，得到的剥离截面呈现出一个多周期振荡结构，非均匀电场对光剥离截面的振荡有显著的增强作用.

1 氢负离子在非均匀电场中光剥离

1.1 体系的哈密顿量

如图1所示，氢负离子被安放在原点，被用于光剥离的激光沿z轴方向.

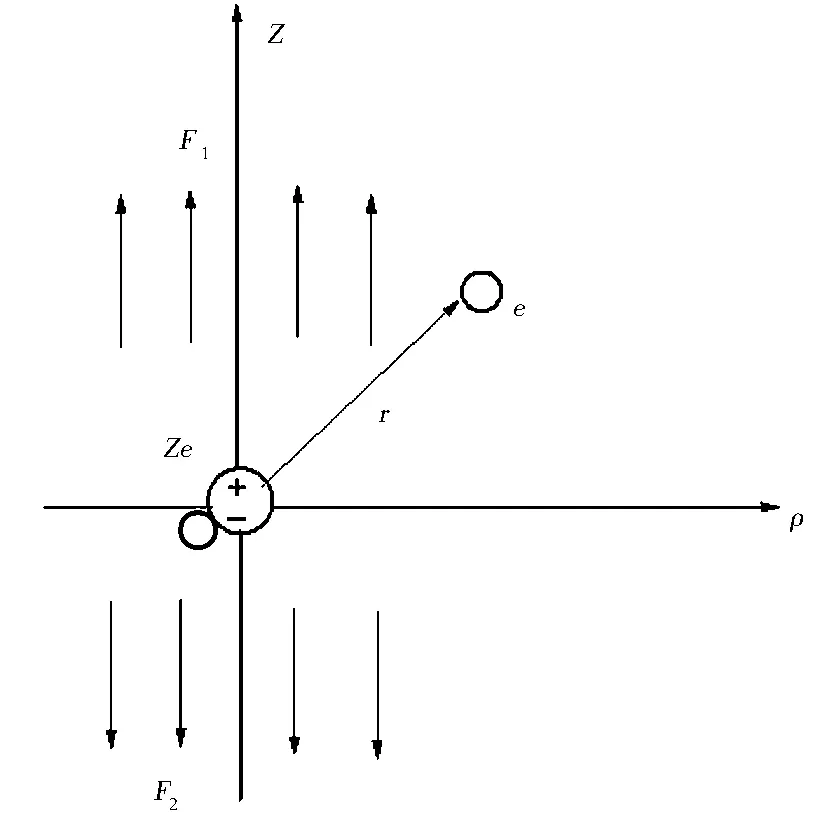
图1 氢负离子在非均匀电场中光剥离示意图

在z>0的半空间中，电场方向沿着+z方向，在z<0的半空间中，电场方向沿着-z方向.其中上半空间的电场强度为F1，下半空间中的电场强度为F2.由于在整个空间中电场的方向是变化的，所以可以把这种情况看做是非均匀电场.结合电子受到的电势能为

(1)

把一个氢原子通过一个短距球对称势Vb(r)的作用，微弱的结合一个电子而得到的单电子系统叫做氢负离子，其中r为被剥离的电子到原点的距离.当氢负离子吸收一个光子时，结合电子就会被剥离，并离开氢原子.在柱坐标系中，剥离电子的哈密顿量可以表示成

(2)

在柱坐标系中，由于角动量的z轴分量Lz保持不变，为了保证角动量守恒，把角动量的z轴分量设为零.此外，当结合电子被剥离而离开氢原子时，短距作用势Vb(r)就可以忽略掉.因此，决定剥离电子运动的哈密顿量可以简化为

(3)

氢负离子在非均匀电场的光剥离的物理图形可以通过半经典闭合轨道理论描述，当氢负离子被一束激光照射的时，负离子将会吸收一份为Eph的光子能量，出射电子将以出射波形式离开核心区域.当波传播的足够远时，将会沿着半经典轨道传播.由于非均匀电场的作用，一些出射电子在运行一个周期后将回到原点，而另一些不能回到原点.能够返回原点的电子将形成返回波，这样返回波和出射波就会相遇而发生干涉，这就会造成光剥离截面的振荡结构.那些起始于中心区域并终结于中心区域的轨道我们称为闭合轨道，这些闭合轨道对光剥离截面的振荡起着重要的贡献.

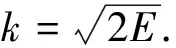
通过解方程(3)，电子在ρ方向的运动方程为：

ρ(t)=Rsinθ+ktsinθ

(4)

由于上半空间中和在下半空间的电场方向不同，必须分别求正z轴方向和负z轴方向的运动方程.在上半空间，即z>0区域,可以得出运动方程：

(5)

在z<0的区域内，运动方程可以写为

(6)

根据以上运动方程，画出剥离电子在非均匀电场中的运动轨迹. 图2中给出了剥离电子的运动轨迹.

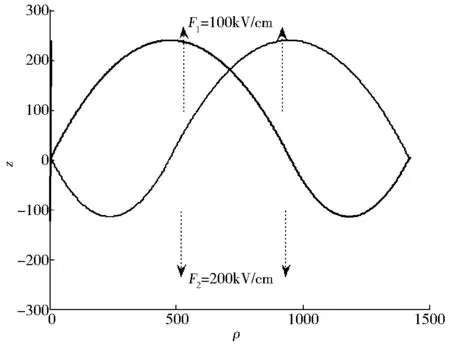
图2 剥离电子在非均匀电场中的轨迹，剥离电子的能量E=0.25eV

从图2中发现，由于ρ轴方向的分运动，只有那些沿z轴出射的电子才会被电场拉回原点.如果被剥离电子沿着+z方向运动，电场将产生一个向下的力，电子的动能首先逐渐减少至零.然后剥离电子将会在电场的作用下回到原点.那些沿着-z方向的剥离电子，由于电场方向的改变，剥离电子亦会在电场的作用下回到原点.所以，向下的电子的运动也是一种减速运动.在运动了一个周期后剥离电子将会回到原点.剥离电子一共会有四种不同的闭合轨道，其他的一些闭合轨道是这四种基本闭合轨道的组合.四种闭合轨道具体情况如下：(Ⅰ)电子沿着+z方向运动，当到达最远距离时，在势能的作用下将会折返并回到原点.这种情况我们叫做向上闭合轨道.(Ⅱ)电子沿着-z方向运动，当达到最远距离时，将会由于势能作用回到原点.这种情况叫做向下闭合轨道.(Ⅲ)电子首先向上运动完成向上闭合轨道，回到原点后穿过原点继续向下运动，并同时完成向下闭合轨道运动.(Ⅳ)这种闭合轨道形式相似于(Ⅲ)形式，但是完全是相反的形式，电子首先向下运动完成向下闭合轨道，然后穿过原点，继续向上运动完成向上闭合轨道.这四种基本的闭合轨道的形式如图3a-3d所示.

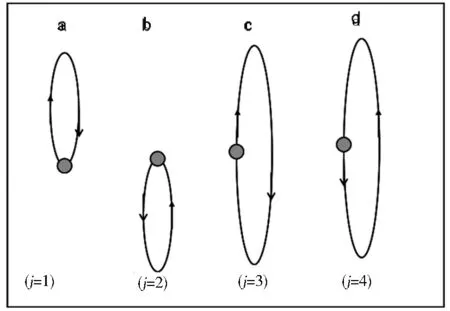
图3 光剥离电子在非均匀电场中的四种基本的闭合轨道

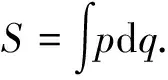
(7)

多轨道的拓扑结构可以通过马斯洛夫指数来描述.在当前系统下，马斯洛夫指数可以很容易地通过计算返回点的数目得到，从而得到

μ1=μ2=1,μ3=μ4=2

(8)

除这四种基本的闭合轨道，还有一些由这四种基本闭合轨道组合而成得到的闭合轨道.这些闭合轨道可以用两个指数标记(j,n)，其中j=1,2,3,4，n=0,1,2,…[17].当n=0时，代表着如图3中a-d中描述的四种基本的闭合轨道.对于其他的闭合轨道(j,n≠0)，可以认为是这四种基本的闭合轨道的组合或者是轨道(j=3,n=0)和轨道(j=4,n=0)循环了n次而得到[17].例如，(j=1,n=1)闭合轨道可认为是(j=1,n=0)闭合轨道和一个(j=3,n=0)闭合轨道的组合，图3中e给出了这种轨道的情形.任意闭合轨道的周期、作用量和马斯洛夫指数(j,n)可通过如下公式求出[19]：

Tjn=Tj+nT,Sjn=Sj+nS

(9)

μ1n=μ2n=2n+1,μ3n=μ4n=2n+2

(10)

1.2 光剥离截面

根据闭合轨道理论，氢负离子在非均匀电场中的光剥离截面可以分成两个部分[19]：

σ(Eph,F)=σ0(Eph)+σosc(Eph,F)

(11)

其中σ0(Eph)是氢负离子在自由空间中的光滑背景项：

(12)

式中：c代表光速，约为137a.u.；B=0.31522为归一化常数；Eph是光子的能量；Eph=E+Eb；剥离电子的结合能为Eb=0.754eV；σosc(Eph,F)为对应于剥离电子返回波的振荡项.

(13)

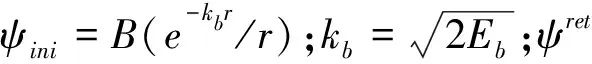
为了得到其他闭合轨道的返回波函数，我们运用了半经典轨道理论研究了出射波的传播.我们假定一个半径为R≈5a.u.的球，并计算得到了球表面上的出射波函数ψ0(R,θ,φ)为[19]

(14)

根据半经典闭合轨道理论，球外面的返回波波函数ψret依赖于电子波初始发射状态：

(15)

求和遍及所有离开或者返回氢原子的电子所构成的闭合轨道，Ajn是闭合轨道(j,n)的振幅.剥离电子的经典运动中，振幅Ajn等同于在均匀电场中所给出的值[19].

(16)

Tjn为闭合轨道(j,n)的周期；Sjn和Tjn以及μjn已经在式(9)和(10)中给出.在球内，波函数可以用沿z方向传播的平面波来近似

(17)

其中-号对应于沿-z轴方向传播的波，+号对应于沿+z轴方向传播的波；Njn为下式给出的常数：

(18)

在当前体系中，包含四种基本的闭合轨道和这四种闭合轨道的组合，所以总的返回波为每个返回波的和：

(19)

把式(19)代入式(13)中并做多重积分，我们得到剥离截面的振荡部分

σosc(Eph,F)=

(20)

h(jn)是标记因子，对于向下或者向上闭合轨道，h=-1；另外两个基本闭合轨道h=1.

所以，总的光剥离截面为：

σ(Eph,F)=σ0(E)+

(21)

1.3 光剥离截面的标度变换

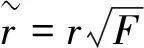
(22)

(23)

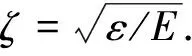
(24)

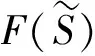
2 计算结果和讨论

根据式(21)，我们先设定沿+z轴方向的电场强度不变F1=100kV/cm，而改变沿-z轴方向的电场强度F2的大小，F2的取值从0变化到1 000kV/cm.在此非均匀电场中的光剥离截面如图4所示.其中实线为氢负离子在非均匀电场中的光剥离截面，虚线为在均匀电场中的光剥离截面.从图4中可以了解到，当一个方向上的电场确定时，另一个方向的电场很小时，两条曲线几乎重合，这时非均匀电场的影响可以忽略.如图4(a).当不断增大电场强度，当向下的电场增加到与向上的电场大小一样时，如图4(b).继续增大电场，当向下的电场比向上的电场大的时候，出现了一些新的情况，如图4a-4f所示.光剥离截面除了有一个多周期振荡的结构外，又多了一些小的振荡.并在大周期结构上镶嵌了一些小的周期结构.这种情况并不断随着电场强度的增加而逐渐显著.当两个方向的电场强度相差很大的时候，光剥离截面的振荡结构就演变为一个类似正弦曲线的结构，另加上一些小的振荡.

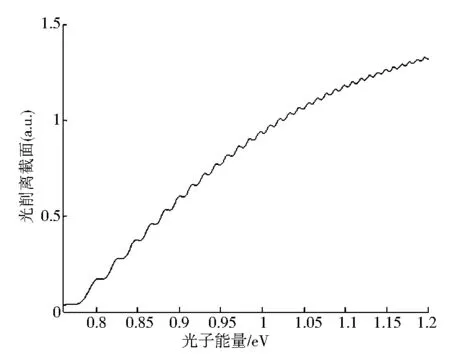
(a)F2=1kV/cm

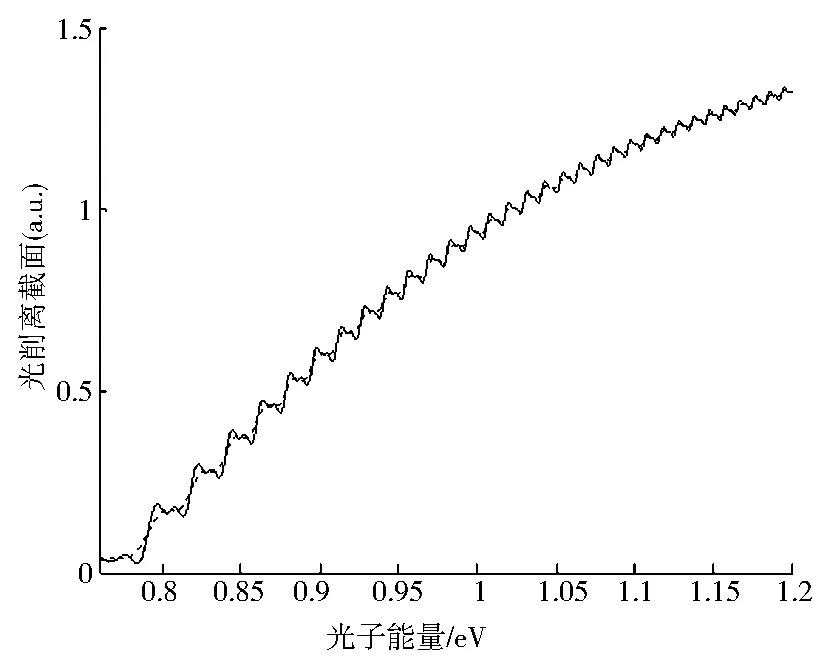
(b)F2=100kV/cm

(c)F2=200kV/cm

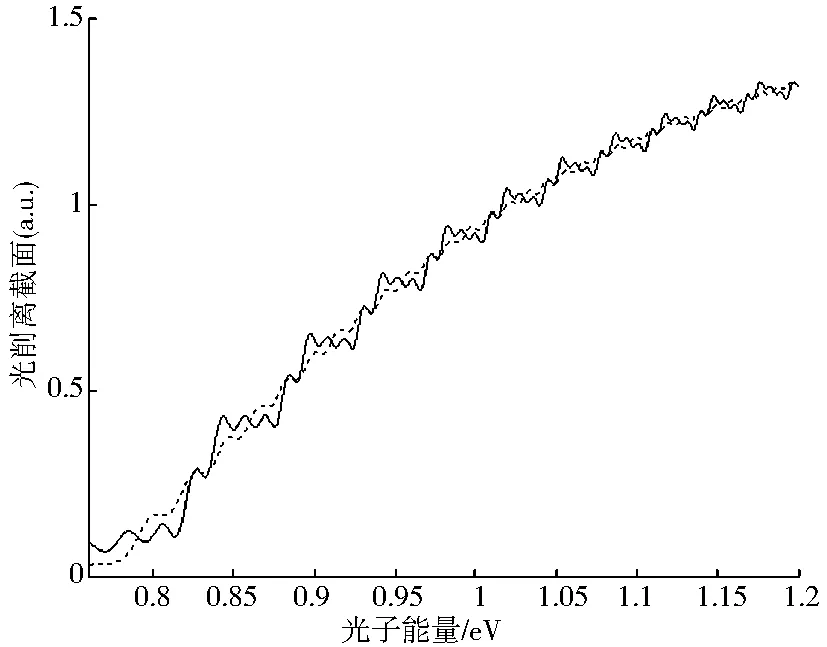
(d)F2=300kV/cm

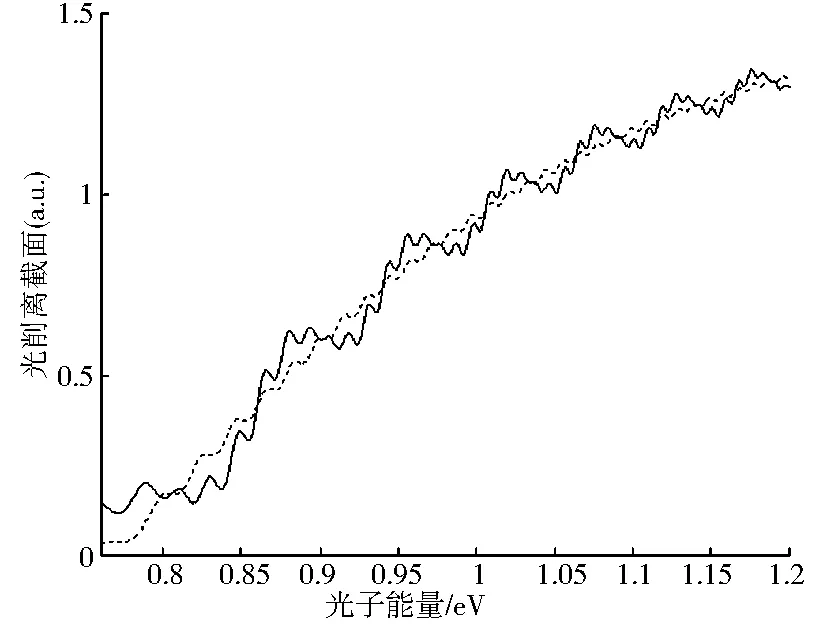
(e)F2=500kV/cm

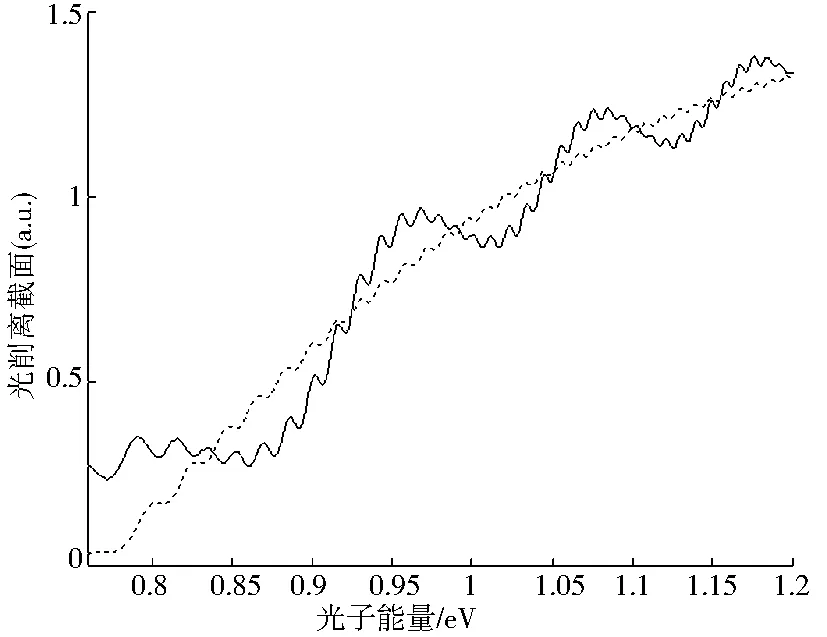
(f)F2=1000kV/cm图4 设定一个方向上的电场强度不变F1=100kV/cm，而改变另一个方向的电场强度F2大小

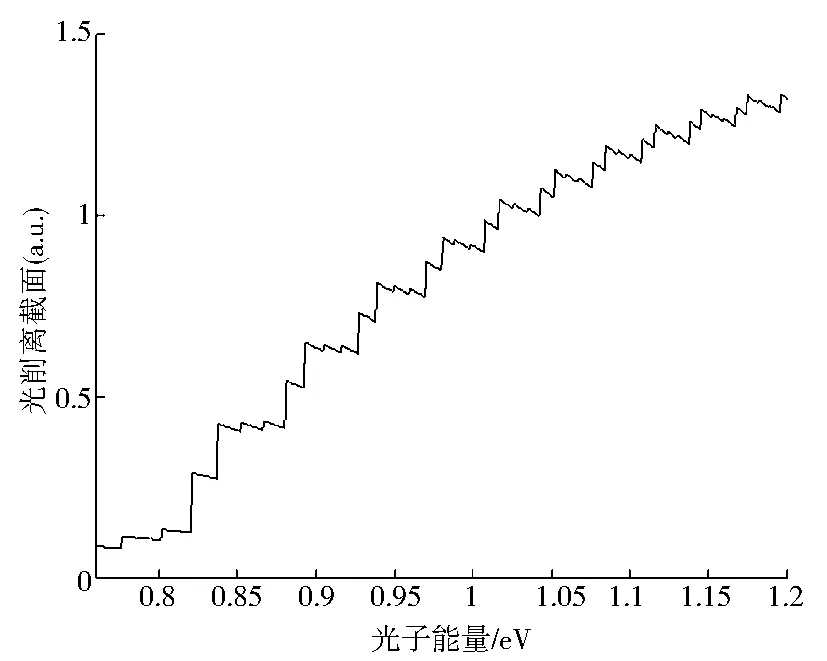
通过闭合轨道理论，当上下平面的电场强度大小相差越大时.向上运动的闭合轨道的周期和作用量就跟向下运动的闭合轨道的周期、作用量相差就越大.因此，周期和作用量的不同又会造成一些振荡结构.随着电场强度大小的差异加大，这种周期和作用量的差异也会加大，从而造成向上和向下的光剥离截面差异加大，由此造成总光剥离截面的多周期振荡结构的加剧.图5中展示的为氢负离子在非均匀电场中1 000条闭合轨道的光剥离截面.并通过同样的方法改变电场大小.和上下空间电场强度大小相同时的情况不同，光剥离截面的阶梯中结构中，又出现了一些小阶梯状结构.当电场大小一定时，阶梯状的大小就会随着光子能量的增加而减小.另外，当增加一个方向的电场强度大小，就会有更多地小的阶梯状结构出现，在图5a-5d中这种情况进行了列举.

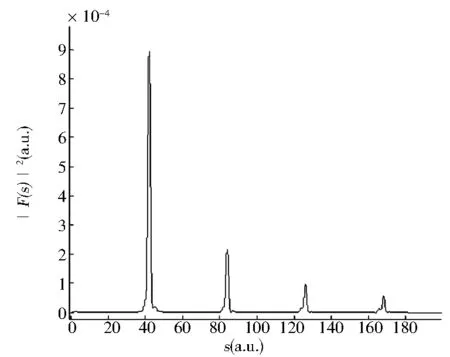
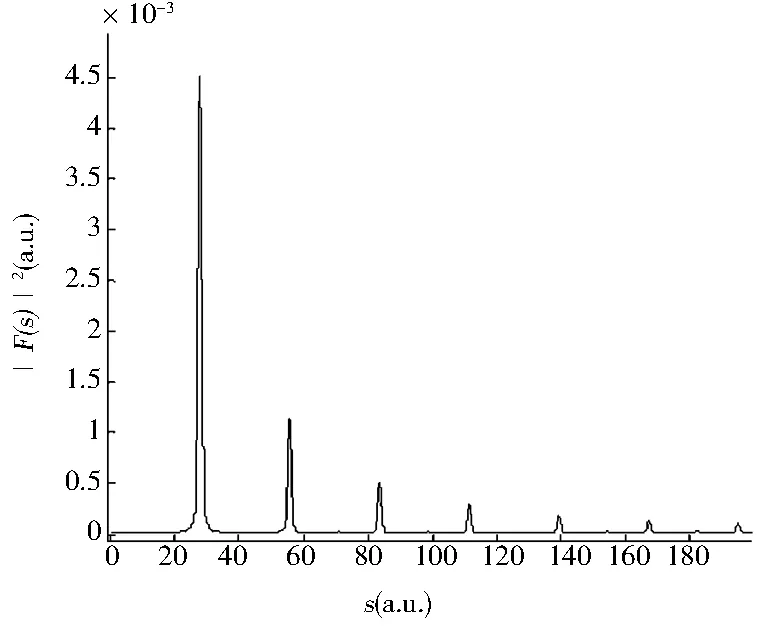
为了清楚地了解光剥离截面和闭合轨道的关系，通过式(24)在不同标度能量下对氢负离子在非均匀电场中的光剥离截面做了傅里叶变换.同样在计算中设定ζ=1和ζ=10两种情况，计算结果如图6所示.每个图中都出现一系列尖峰，每一个尖峰都有一个相应的闭合轨道与之对应.例如，在图6(a)中第一个峰出现在41.80处，与之相对应的为向上或者向下的闭合轨道.第二个峰出现在83.60处，对应着第三和第四个闭合轨道.第三个峰出现在123.24处，与之对应的是向下、向上的闭合轨道跟第三或者第四条闭合轨道的组合.依据这些，在图6(a)和6(b)中画出了每一个峰.可以发现，随着缩放能量的减小，得到的峰的数目却在增多，正如6a-6d所示.

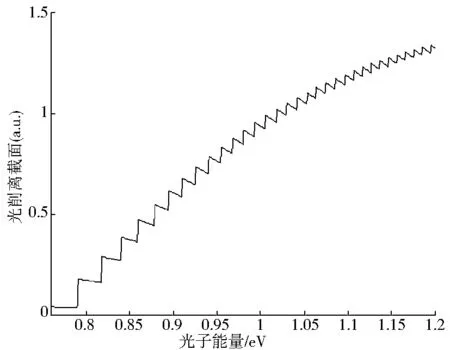
(a)F2=100kV/cm

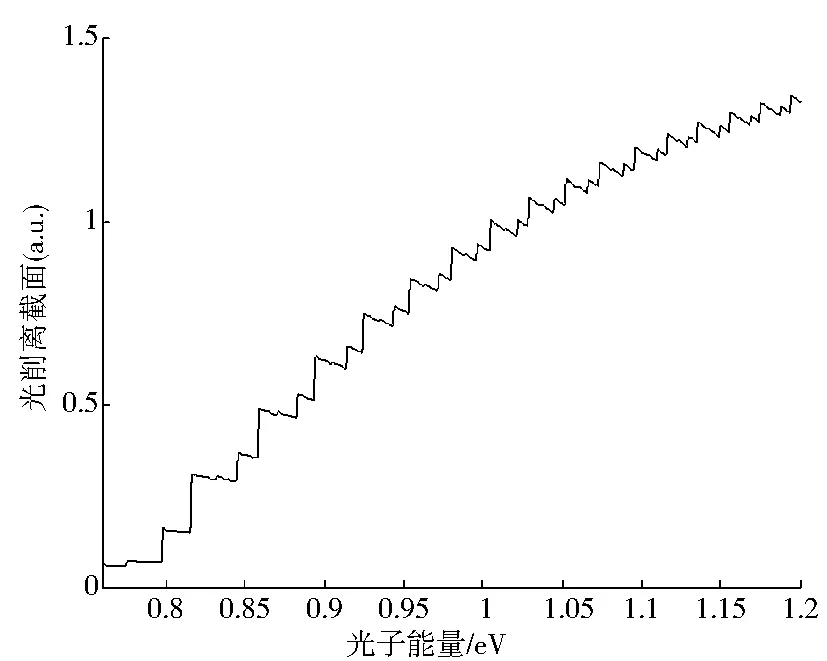
(b)F2=200kV/cm

(c)F2=300kV/cm

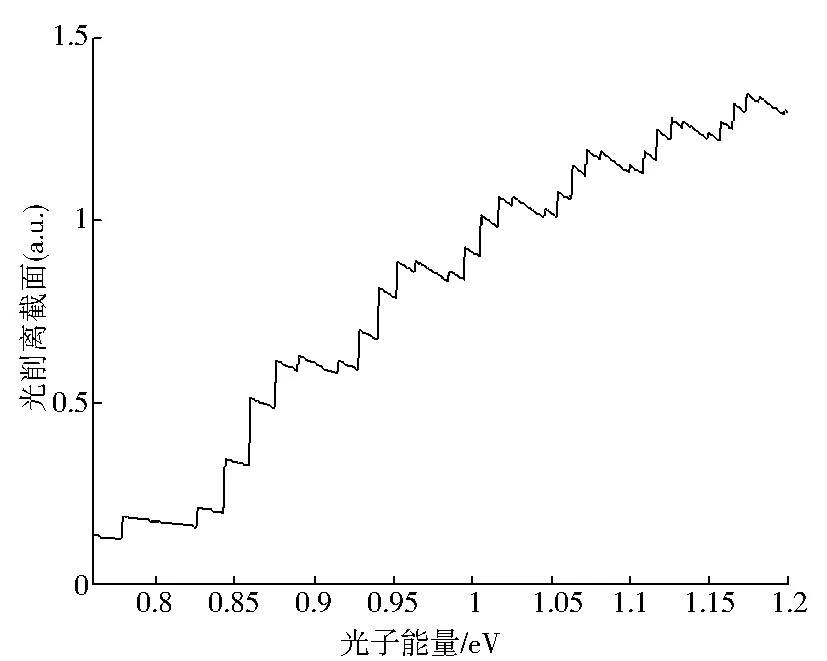
(d)F2=500kV/cm图5 氢负离子在非均匀电场中1000条闭合轨道情况的光剥离截面(F1=100kV/cm)

(a)ε=1.45

(b)ε=1.18

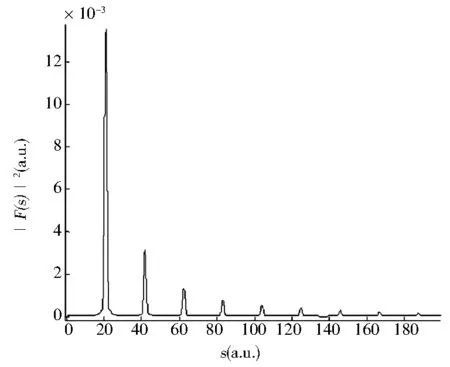
(c)ε=1.02

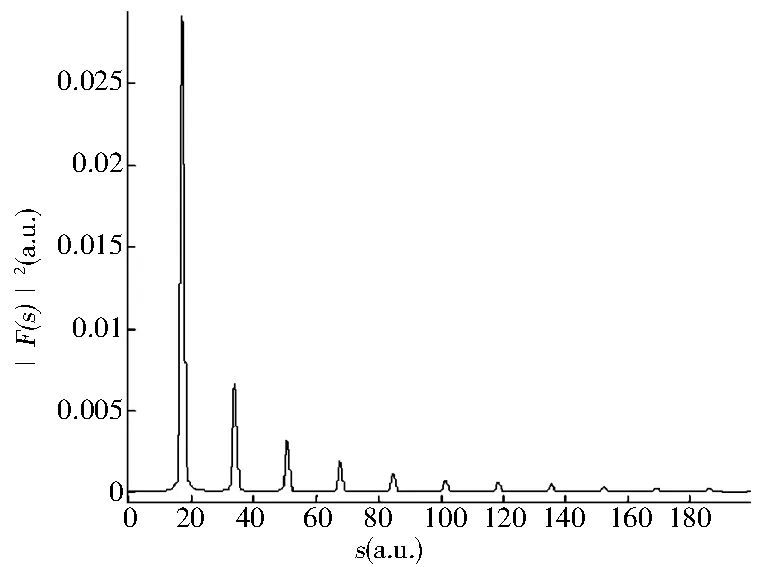
(d)ε=0.92图6 氢负离子在非均匀电场中的光剥离截面在不同的标度能量下的傅里叶变换

3 结束语

利用闭合轨道理论对氢负离子在非均匀电场中的光剥离进行了研究,对体系的光剥离截面进行了计算和分析.与氢负离子在均匀电场中的光剥离相比较，剥离电子的闭合轨道的数目增加，光剥离截面的振荡情况更加复杂，表现出一个多周期振荡结构.对这个体系的光剥离截面进行的傅里叶变换，给出清晰的光剥离截面的振荡结构和剥离电子的闭合轨道之间的关系，揭示了峰值随缩放能量的变化规律.

[1] Bryant H C. Observation of motional-field-induced ripplesin the photodetachment cross section of H-[J].Phys.Rev.Lett.,1987, 58(6): 2 412-2 415.

[2] Du M L. Photodetachment spectra of H-in parallel electric and magnetic fields[J].Phys.Rev.A., 1989,40(2):1 330-1 333.

[3] Peters A D, Jaffe C, Delos J B. Closed-orbit theory and the photodetachment cross section of H-in parallel electric and magnetic fields[J].Phys.Rev.A., 1997, 56(6):331-334.

[4] Peters A D, Delos J B. Photodetachment cross section of H- in crossed electric and magnetic fields. I. Closed-orbit theory[J]. Phys.RevA., 1993,47(6):3 020-3 023.

[5] Peters A D, Delos J B. Photodetachment cross section of H- in crossed electric and magnetic fields. II. Quantum formulas and their reduction to the result of the closed-orbit theory[J].Phys.Rev A., 1993,47(3):3 036-3 039.

[6] Peters AD, Jaffe C, Delos J B. Quantum Manifestations of Bifurcations of Classical Orbits: An Exactly Solvable Model[J].Phys.Rev.Lett.,1994,73(2):2 825-2 828.

[7] Liu Z Y, Wang D H, Lin S L. Photodetachment cross section of H-in electric and magnetic fields with any orientation[J].Phys. Rev.A., 1996,54(6):4 078-4 081.

[8] Liu Z Y, Wang D H. Analyzing the photodetachment cross section of H-in electric and magnetic fields with arbitrary orientation[J].Phys.Rev.A., 1997,55(3):4 605-4 608.

[9] Liu Z Y, Wang D H. Quantum-mechanical calculation of the photodetachment of in electric and magnetic fields with arbitrary orientation[J].Phys.Rev.A., 1997,56(2):2 670-2 673.

[10] Yang G C, Zheng Y Z , Chi X X. Photodetachment of H-in a static electric field near an elastic wall[J].Phys.Rev.A.,2006,73(6):043413-043416.

[11] Huang K Y, Wang D H. The influence of electric field on the photodetachment of H near a metal surface[J].Chin. Phys. B., 2010,19(6): 063402-063405.

[12] Wang D H, Tang T T , Wang S S. Influence of the oscillating electric field on the photodetachment of H- near a metal surface[J].J.Phys. Soc. Jpn., 2011, 80(2):094301-094304.

[13] Yang B C , Du M L. Modifying the photodetachment near a metal surface by a weak electric field[J].Mol. Opt. Phys., 2010,43(3): 035002-035005.

[14] Du M L, Delos J B. Effect of closed classical orbits on quantum spectra: Ionization of atoms in a magnetic field. I. Physical picture and calculations[J]. Phys.Rev.A., 1988, 38(6)：1 896-1 899.

[15] Du M L, Delos J B. Effect of closed classical orbits on quantum spectra: Ionization of atoms in a magnetic field[J].Phys.Rev.Lett., 1987,58(2):1 731-1 734.

[16] Han Y, Wang L F, Yang N Y ,etal. Coexistence and extinction pattern of asymmetric cyclic game species in a square lattice[J].Phys B., 2010,405(5):3082-3085.

[17] Yang G, Mao J M, Du M L. Photodetachment cross section of in a gradient electric field[J].Phys. Rev. A, 1999, 59(2):2053-2056.

[18] Du M L. Closed-orbit theory for photodetachment of H-in a static electric field[J].Phys.Rev.A., 2004,70(6):055402-055405.

[19]Wang Y H, Wang D H, Li J W. Photodetachment of H in a non-uniform electric field[J]. Can.J.Phys.,2013, 91(6): 650-656.