带五种被动阻尼器的高层建筑侧移—扭转下随机风振响应的解析法
2014-03-20王俊波李创第葛新广
王俊波 李创第 葛新广
1河南理工大学土木工程学院(454000)2广西科技大学土木建筑工程学院(545006)
带五种被动阻尼器的高层建筑侧移—扭转下随机风振响应的解析法
王俊波1李创第2葛新广2
1河南理工大学土木工程学院(454000)2广西科技大学土木建筑工程学院(545006)
对带被动阻尼器的高层建筑考虑侧移-扭转情况下,随机风振响应和等效风载取值进行了研究。针对文献[3]获得了设置五种被动阻尼器的高层建筑,考虑侧移-扭转效应下统一非经典的结构运动方程,这里用复模态法解耦,并用随机振动方法,获得了带五种被动减振器的高层建筑考虑侧移-扭转反应基于现行规范Davenport谱随机风振响应的解析解,并给出算例。
被动阻尼器;侧移-扭转;复模态法;等效风荷载取值
0 引言
随着高层建筑结构的增多,风致振动引起的高层建筑不能满足结构刚度和舒适度的抗风设计要求的问题日益突出。因此,越来越多的研究者致力于用结构振动控制的方法来解决上述问题。被动阻尼器是一类既简单又对高层建筑脉动风振反应有较好控制效果的减振装置,在国内外都已获得了研究成果,受到了一定的应用[1~2]。此前结构随机风振响应分析方法主要有频域法[3]、数值积分[4]、随机平均法[5]等。这里利用瞿伟廉教授建立的五种被动动力减振器高层建筑侧移—扭转脉动风振反应控制的统一公式[3],对此类结构按第一振型展开后,采用复模态法进行解耦,获得了与我国现行规范所采用的Davenport谱对应的以第一振型表示的结构随机风振响应解析解。
1 运动方程
设一个n层高层或高耸结构设置L个被动减振器,在顺风向的脉动风荷载作用下,瞿伟廉教授建立了设置被动动力减振器的高层建筑的侧移—扭转脉动风振反应的统一方程为[3]:


2 方程解耦的复模态法
采用复模态理论进行解耦。令:

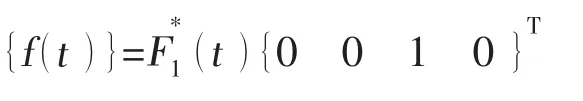
根据文献[10],式(3)的左、右特征向量V[]、U[]关于[Me]、[Ke]带权正交。即:

引入复模态变换令:

则方程(3)可解耦为[6-8]:

式中:

[U]、[V]、[P]=diag[Pj]分别为方程(3)的右、左特征向量矩阵和特征值矩阵。
3 随机风振响应计算
3.1基于现行规范的Davenport风谱的风载激励模型
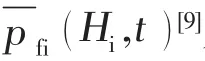

上式中,IO(Hi)为方差等于1的随机变量,k为与地面粗糙度有关的系数。
)为脉动风荷载标准差,
,分别为风压高度变化系数、体型系数和当地基本风压,q (t)仅为时间t的随机过程,其均值为零,具有规格化功率谱即
顺风向脉动风荷载的功率谱密度函数Suiuj(ω)、扭转风力向量的功率谱密度函数Sθiθj(ω)、迎风面脉动风力向量和扭转风力向量的互功率谱密度函数Suiθj(ω)分别为:

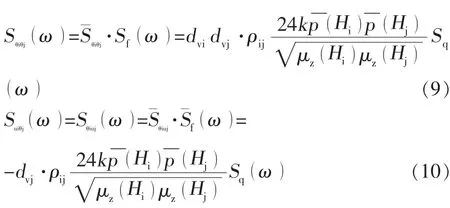
)为相关函数,k为与地面粗糙度有关的系数,z
i
、z
j
为第i、j层的离地面高度;d
vi
和d
vj
分别为结构第i和第j层迎风面脉动风力气动中心相对于质量中心的v坐标。
结构第一振型广义荷载的F*1(t)自功率谱密度函数为:

3.2 结构响应方差分析
由(4)、(6)、(9)方程得(6)的分量形式:

式中:

可求得xi的响应方差[10-14]为:

式中:


Hj(ω)为质量、频率和阻尼比分别为1、ωj、βj的等效单自由度体系的频率相应函数。I1(ωj)和I2(ωj)分别为上述等效单自由度体系在具有规格化Davenport风谱Sq(ω)的随机过程荷载f( t)作用下位移和速度的方差。
4 基于现行规范所采用的Davenport风谱的响应均方差计算


故一旦求出2个等效单自由度体系的风谱Sf(ω)作用下的位移和速度响应的最大值的平方R1(ωj)=c2fI1(ωj)和R2(ωj)=c2fI2(ωj)则在式(27)中,分别用R1(ωj),R2(ωj)代替I1(ωj)和I2(ωj)即可求得R2(xm),对其开方,即得xm(t)的设计响应R( xm)。由于:

由于文献[11]已经求得I1(ωj)及I2(ωj)的解析解,故由式(17),即得R1(ωj)及R2(ωj)的解析解。
5 等效风荷载取值计算
由于原结构按第一振型展开,即

故原主体结构各楼层风振位移响应设计值为

对原主体结构,其刚度矩阵[K]、质量矩阵[M]与第一振型和第一频率ω01有如下关系:
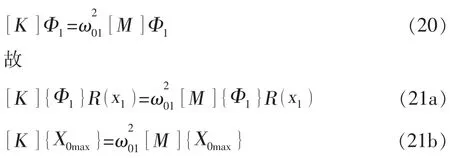
故原主体结构等效风振力设计值向量Pd与该楼层的风振位移响应设计值X0max有如下关系:

其中:M0为原主体结构的质量矩阵,φi1为原主体结构的第一振型。
考虑到结构总的风效应Pi可看成是平均风力和等效风振力共同作用的总效应,于是可得结构第i层顺风向的等效静力风荷载:

第i层扭转方向等效风荷载为:

第i层横风向等效风荷载为:

6 算例
某海边一个8层钢结构建筑,在结构第6、7、8各设置一个TMD系统。该建筑层高均为3.5 m,每层质量为140 t,每层迎风面积为105 m2,结构第一振型阻尼比ξ1=0.01,结构自振周期T1=1.256 s,结构第一自振圆频率ω01=2π/T1=5(rad/s),质心与刚心只在Y方向存在偏心。X方向有单向风载输入,结构产生沿轴的平动和绕竖直轴的转动;每层质心与刚心的距离为0.86 m;顺风向第一振型{φu1}=[0.239 9 0.471 0 0.619 2 0.747 4 0.851 6 0.928 4 0.975 3 1.000 0]T,横风向第一振型{φv1}=[0.1433 0.2811 0.369 0 0.444 7 0.505 8 0.550 1 0.578 0 0.593 2]T,扭转方向第一振型{φθ1}=[0.013 4 0.022 4 0.030 1 0.034 4 0.037 1 0.039 3 0.0400 0.051 2]T,取TMD与结构第一振型广义质量M*0比为0.025,TMD的频率为5(rad/s),TMD的阻尼比为0.05,当地基本风压为0.6 kN/m2。图1、2、3画出了结构设置3个TMD后,用复模态法得到的结构各层顺风向、横风向和扭转方向风振位移响应设计值解析解,和结构不带TMD时结构响应的对比曲线。表1、2、3列出了有无TMD控制的结构各层的顺风向、横风向和扭转方向等效静态设计风荷载。可以看出,用复模态获得的解析解与用频率法和数值积分法获得的数值解基本一致,与无TMD控制相比,结构顺风向等效静态风荷载减少了12.2%~25.5%,结构扭转方向等效静态风荷载减少了1.4%~3.4%,结构顺风向等效静态风荷载减少了35.5%。可见,TMD减振效果是很明显的,尤其是对结构在横风向的控制效果更为明显。

图1 各楼层顺风向风振位移响应的设计值

图2 各楼层扭转方向风振位移响应的设计值
7 结论
这里对设置五种被动阻尼器(TMD、TLCD、LCVD、C-TLD、R-TLD)的高层建筑考虑侧移-扭转随机风振响应等效静态设计风载取值进行了研究,有助于将复杂的随机振动响应转化为简单的等效静态设计法。

图3 横风向风振位移响应的设计值

表1 各楼层顺风向等效静态设计风荷载值(kN)

表2 各楼层扭转向等效静态设计风荷载值(kN·m)

表3 各楼层横风向等效静态设计风荷载值(kN)
由于获得了上述五种被动控制高层建筑风振试验研究响应的解析解,故一方面可对结构进行抗风动力可靠性分析[12],另一方面可进一步利用此解析解,对结构待定控制参数进行优化设计,在给定控制装置动力响应不超过某一设计限值的动力可靠度约束条件下,通过主体结构的响应方差取极小值条件,用罚函数方法等优化方法,可直接确定控制装置的待定优化参数[13、14],实现主体结构的最优抗风控制设计,建立基于动力可靠性约束的带被动阻尼器的高层建筑结构抗风优化控制设计方法。
[1]欧进萍,等.设置TMD、TLD控制系统的高层建筑风振分析与设计方法[J].地震工程与工程振动,1994(6):61~75.
[2]黄文俊,等.几种常见阻尼器的减振特性分析[J].北京:地震工程与工程振动,2007(7):42~48.
[3]瞿伟廉,等.C C Chang.应用五种被动动力减振器时高层建筑侧移-扭转脉动风振反应控制优化设计的统一公式[J].地震工程与工程振动,2008(2):137~146.
[4]李春祥,刘艳霞.高层建筑TMD风振控制优化设计[J].计算力学学报,2001(1):69~73.
[5]李创第,骆鸿林,陆运军,余亚平.Maxwell粘滞阻尼器耗能结构的风振响应与等效风荷载取值[J].广西工学院学报, 2011,22(3):7~11.
[6]李创第,李暾.高层建筑TMD风振控制分析的复模态法[J].振动与冲击,2003(2):1~4.
[7]李创第,黄天立.基础隔震结构随机地震响应分析的复模态法[J].地震工程与工程振动,2002,22(6):122~128.
[8]李创第,黄天立.带TMD结构随机地震响应分析的复模态法[J].振动与冲击,2003,22(1):36~39.
[9]杨庆山.悬索结构随机风反应分析[J].建筑结构学报,1998 (4):29~39.
[10]李创第,等.带五种被动减振器的高层建筑基于Davenport谱随机风振响应的解析解法[J].2009,26(4):144~152.
[11]李桂青.工程结构时变可靠度理论及其应用[M].北京:科学出版社,2001:201~204.
[12]李创第.高层建筑玻璃幕墙线性与非线性抗风动力可靠性分析(2)[J].工业建筑,1999,29(6):17~19.
[13]李创第,黄天立.带TMD结构基于动力可靠性约束的抗震优化设计[J].地震工程与工程振动,2004,24(6):121~125.
