关于局部扭立方体的反馈数

张思佳，徐喜荣＊，刘 聪，曹 楠，杨元生

（1.大连理工大学 电子信息与电气工程学部，辽宁 大连 116024；2.中国科学技术大学 数学系，安徽 合肥 230026）

0 引 言

在组合网络理论中，若一个简单图删除某些节点后构成的导出子图不存在回路，则称被删去的节点集合为该简单图的反馈点集.阶数最小的反馈点集称为最小反馈点集，最小反馈点集的阶数叫做反馈数.

确定图的最小反馈点集问题，因其在诸多领域内的广泛应用而受到重视.例如在互联网中，如果网络有回路，广播消息会一直在网桥环网中传递，形成“广播风暴”，阻塞网络.解决这个问题的做法就是想办法尽可能少地关闭一些网桥，使剩下的网络不再有回路［1］.再如：任何一个具有自动化功能的工作单位，都需要不断地发出指令，再分析指令执行的结果，然后发出新的指令，用以调整或改变工作状态.持续不断的反馈是自动化得以实现的关键.另外，在操作系统和超级计算机的分布式计算中避免死锁产生的问题，同样也是确定网络反馈点集的问题［2］.

因为确定一般网络（或图）的最小反馈点集问题属NP 难问题［3］，所以现阶段还不能对这一问题给出令人满意的结论.尽管在一些文献中，对某些特殊拓扑结构图（如mesh网络、toroids网络、butterflies网络、立方连通网络、超立方体网络和星图等）的反馈数的上界和下界都已经陆续得到［4－19］，但即使是得到了具体的图，要确定其最小反馈集仍不是容易的事.

本文根据局部扭立方体顶点集合中最后一位字节不同的特点，将其顶点集合划分为两个不相交的子集，并构造极大无圈子图得到反馈数的上界，从而研究局部扭立方体的反馈数问题.

1 定义和引理

n维局部扭立方体（locally twisted cube）简称为Qltn（n≥2），由Yang等［14］于2005年提出.Qltn网络是超立方体网络Qn的变形.与n维超立方体Qn类似，Qltn是一个具有2n个顶点的n－正则图，顶点集由n维的｛0，1｝字符串组成.但Qltn相比Qn有许多好的性质，例如在维数相同的情况下，Qltn具有比Qn更小的半径；Qltn能嵌入所有长度为l（4≤l≤2n）的圈，圈嵌入能力优于Qn.有关局部扭立方体的其他性质，可参阅文献［3，4，10－13，15 －19］.

定义1Qltn的边集由这样的边组成：对任意两个顶点x＝x1x2…xn和y＝y1y2…yn，它们之间进行连边，当且仅当它们满足如下要求之一：

（1）存在一个整数k（1≤k≤n－2）满足yk是xk的补点，xk∈｛0，1｝），yk＋1＝（xk＋1＋xn）mod 2，x和y的其余字节均相同（x和y仅有连续两位字节不同），此时（x，y）称为非匹配边；

（2）存在一个整数k∈｛n－1，n｝，x和y仅在第k位不同，其余字节全相同，则x和y存在连边，并称（x，y）为匹配边.

由上述定义不难发现，Qlt2由标记为00、01、10和11的4个顶点以及4条边（00，01）、（00，10）、（01，11）、（10，11）组成.

当n≥3，Qltn由两个不相交的Qltn－1图添加2n－1条边组成，其按照如下步骤构建：在其中一个Qltn－1的所有顶点的二进制串前面加上一个前缀0，用0Qltn－1表示；其中的另外一个Qltn－1的所有顶点的二进制串前面加上一个前缀1，用1Qltn－1表示；用一条边连接图形0Qltn－1中的顶点x＝0x2x3…xn和图形1Qltn－1中的顶点x＝1（x2＋xn）x3…xn，这里“＋”表示模2 加法.通常，记为Qltn＝LR，其中L0Qltn－1，R1Qltn－1.如图1所示.

定义2 图G中两两互不相邻的顶点构成的集合S称为图G的独立集.

Beineke等［15］证明了一般图G＝（V，E）的反馈数的下界为

其中Δ＝Δ（G），为图G的最大度.由于Qltn是n－正则图，Qltn的最小度Δ＝n且所以得到如下Qltn的反馈数的下界.

引理1 令f（n）表示Qltn的反馈数，则有

2 局部扭立方体的反馈数的上界

定义3 对于局部扭立方体Qltn，顶点x＝x1x2…xn∈V（Qltn）.定义：

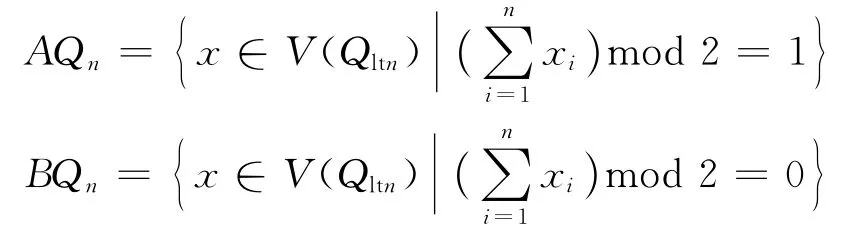
显然，AQn是Qltn的所有奇顶点构成的集合，BQn是Qltn的所有偶顶点构成的集合，且V（Qltn）＝AQn∪BQn，AQn∩BQn＝.

定义4 把顶点集合V（Qltn）与字符串b＝y1y2…yj（yi∈｛0，1｝，1≤i≤j）连接，定义为Qbltn＝｛xb｜x∈V（Qltn）｝，bQltn＝｛bx｜x∈V（Qltn）｝.把二进制字符串b和含有二进制字符串元素的集合Q连接，定义为Qb＝｛xb｜x∈Q｝，bQ＝｛bx｜x∈Q｝，其中xb代表字符串x与字符串b连接组成的一个新字符串，bx代表字符串b与字符串x连接组成的一个新字符串.

通常，由Qltn＝0Qltn－11Qltn－1知，可根据第一位字节的不同将Qltn的顶点划分为两个不相交的子集.

本文给出一种新的划分方法：根据最后一位字节的不同将Qltn的顶点划分为两个不相交的子集.

取T0n－1＝｛x＝xn－1xn－2…x10｜x∈V（Qltn）｝，则有

即T0n－1与M1n－1为Qltn的顶点划分的两个不相交的子集.

由Qltn的定义，任意选取x＝xn－1xn－2…x10∈T0n－1，存在唯一一个点y＝xn－1xn－2…x11 ∈M1n－1，使得x与y之间有边相连.

首先给出新划分的两个不相交的子集T0n－1与M1n－1的性质.

引理2 令G0＝G（Tn0－1），G1＝G（Mn1－1），那么G0＝G（Qn0－1）且G1＝G（Qn1－1）.

证 明 显 然，V（G0）＝Q0n－1＝｛x0｜x∈V（Qn－1）｝，只需证明E（G0）＝E（G（Qn0－1））.

因为G0是Qltn中Tn0－1的导出子图，x，y∈且x和y的最后一位字节都为0.由Qltn定义知，当且仅当x和y只有一位字节不同时存在连边，这与Q0n－1的定义等同，因此E（G0）＝E（G（Q0n－1））.

同理，可证G1＝G（Q1n－1）.证毕.

由M1n－1＝｛x＝xn－1xn－2…x11｜x∈V（Qltn）｝，可以得到：

例如：M12＝｛001，011，101，111｝，则有M2＝｛00，01，10，11｝；

M13＝ ｛0001，0011，0101，0111，1001，1011，1101，1111｝，则有M3＝｛000，001，010，011，100，101，110，111｝.

定义5 令R2＝｛00，01｝，S2＝｛10，11｝，定义集合Rn和Sn如下：

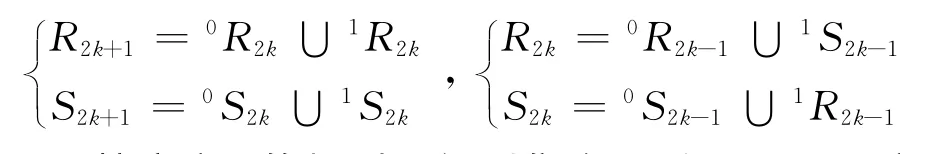
按定义5的规则易得到集合Rn和Sn与Mn之间有如下结果：

根据归纳 可 得Rn∪Sn＝0Rn－1∪1Rn－1∪0Sn－1∪1Sn－1＝0Mn－1∪1Mn－1＝Mn.

因为Mn＝Rn∪Sn，则M1n＝R1n∪S1n.

现在讨论R1n与S1n所诱导的子图之间的关系.

引理3 令G2＝G（R1n），G3＝G（S1n），则G2和G3分别只含有匹配边.

证明 采用归纳法证明.由R2＝｛00，01｝，S2＝｛10，11｝，可得

如图2所示，当n＝3时，G（R13）和G（S13）只含有匹配边.同理，当n＝4时，G（R14）和G（S14）也只含有匹配边.

图2 无圈子图G（R13）、G（S13）、G（R14）和G（S14）Fig.2 The acyclic subgraphs G（R13），G（S13），G（R14）and G（S14）

对n分为奇数和偶数两种情形来归纳证明.

第1种情形：假设当n为偶数时，即当n＝2k时，G（R12k）和G（S12k）含有匹配边，则证明当n＝2k＋1时，G（R12k＋1）和G（S12k＋1）只含有匹配边.

因为R2k＋1＝0R2k∪1R2k，则R12k＋1＝0R12k∪1R12k.由假设G（R12k）含匹配边，则G（0R12k）和G（1R12k）含匹配边.

为证明G（R12k＋1）含有匹配边，只需证明0R12k与1R12k之间各点无连边.用反证法证明，假设0R12k与之间有点相连接，即a∈0R12k，b∈1R12k，a与b有连边，（a，b）∈E（G（R12k＋1））.因为R2k＝0R2k－1∪1S2k－1，则0R2k＝00R2k－1∪01S2k－1，1R2k＝10R2k－1∪11S2k－1；R12k＝0R12k－1∪1S12k－1，则0R12k＝00R12k－1∪01S12k－1，1R12k＝10R12k－1∪11S12k－1.因 此a∈00R12k－1或01S12k－1，b∈10R12k－1或11S12k－1.

由Qltn定义，若（a，b）为非匹配边，则a和b仅有连续两位字节不同，其余全相同.显然，a和b的第一位字节不同，若（a，b）为非匹配边，则第二位字节必不相同.那么，分两种情况考虑：

情况1 如果a∈00R12k－1，则b∈11R12k－1.显然，R12k－1≠S12k－1，则b11S12k－1和b10R12k－1，与假设矛盾；

情况2 如果a∈01S12k－1，则b∈10S12k－1.显然，S12k－1≠R12k－1，则b10R12k－1和b11S12k－1，与假设矛盾.

因此，0R12k与1R12k之 间 各 点 无 连 边，即只含有匹配边.同理，可证G（S12k＋1）只含有匹配边.

第2种情形：假设当n为奇数时，即n＝2k＋1时，G（R12k＋1）和G（S12k＋1）含有匹配边，则证明当n＝2k＋2时，G（R12k＋2）和G（S12k＋2）只含有匹配边.

因为R2k＋2＝0R2k＋1∪1S2k＋1，则R12k＋2＝0R12k＋1∪1S12k＋1.由 假 设G（R12k＋1）含 匹 配 边，则G（0R12k＋1）和G（1R12k＋1）含匹配边.

为证明G（R12k＋2）含有匹配边，只需证明0R12k＋1与之间各点无连边.用反证法证明，假设与1S12k＋1之 间 有 点 相 连 接，即a∈0R12k＋1，b∈1S12k＋1，a与b有连边，（a，b）∈E（G（R12k＋2））.

因 为R2k＋1＝0R2k∪1R2k，则0R12k＋1＝00R12k∪01R12k；S2k＋1＝0S2k∪1S2k，则1S12k＋1＝10S12k∪11S12k.因此a∈00R12k或01R12k，b∈10S12k或11S12k.

由Qltn定义，若（a，b）为非匹配边，则a和b仅有连续两位字节不同，其余全相同.显然，a和b的第一位字节不同，若（a，b）为非匹配边，则第二位字节必不相同.那么，分两种情况考虑：

情况1 如果a∈00R12k，则b∈11R12k.显然，≠S12k，则b11S12k和b10S12k，与假设矛盾；

情况2 如果a∈01R12k，则b∈10R12k.显然，≠R12k，则b10S12k和b11S12k，与假设矛盾.

因此，0R12k＋1与1S12k＋1之间各点无连边，即只含有匹配边.同理，可证G（S12k＋2）只含有匹配边.证毕.

由引理2知，T0n－1＝Q0n－1＝AT0n－1∪BT0n－1，其中AT0n－1为Q0n－1的奇数点集合，BT0n－1为Q0n－1的偶数点集合.AT0n－1和BT0n－1分别是Q0n－1的独立集.

引理4G（AT0n－1∪R1n－1）是Qltn的无圈子图.

证明AT0n－1是Q0n－1的独立集，也是Qltn的独立集，则G（AT0n－1）是不含圈的.由引理3 得，只含有匹配边，则是不含圈的.

因为AT0n－1T0n－1，R1n－1M1n－1，由Qltn定义知，顶点x∈AT0n－1与顶点y∈R1n－1当且仅当最后一位字节不同，其余字节相同时两点之间有连边.即若x与y相连，则x＝xn－1xn－2…x10∈AT0n－1，至多存在一个y＝yn－1yn－2…y11∈R1n－1.因此，G（AT0n－1∪R1n－1）的导出子图是不含圈的.证毕.

由引理4和反馈点集的定义，得下面引理.

引理5V（Qltn）＼（AT0n－1∪R1n－1）是Qltn的反馈点集.

定理1 令f（n）为Qltn的反馈数，则f（n）≤2n－1.

证明 因为则有即2n－1，所以f（n）≤V（Qltn）＼（AT0n－1∪R1n－1）＝2n－2n－1＝2n－1.证毕.

由定理1和引理1，得下面定理.

定理2 任意正整数n≥2且c∈（0，1）时，Qltn的反馈数为

注：事实上，可证G（BT0n－1∪S1n－1）是不含圈的，V（Qltn）＼（BT0n－1∪S1n－1）也是Qltn的反馈点集.因为可 得f（n） ≤V（Qltn）＼（BT0n－1∪S1n－1）＝2n－2n－1＝2n－1，即结合引理1也可得到定理2.

3 结 语

对一般图确定最小反馈点集是一个NP难问题，准确计算出图的最小反馈点集是很困难的.至今，人们只对一些特殊的图给出了求最小反馈点集的多项式时间的算法.本文根据n维局部扭立方体顶点集合中最后一位字节不同的特点，将其顶点集合划分为两个不相交的子集，构造极大无圈子图并得到了局部扭立方体网络的反馈数的上界.

［1］ 周书明.六角形蜂窝网络的反馈数［J］.工程数学学报，2011，28（2）：260－264.ZHOU Shu－ming.Feedback number of honeycomb networks ［J］.Chinese Journal of Engineering Mathematics，2011，28（2）：260－264.（in Chinese）

［2］ 吴叶舟.线图的反馈数［D］.合肥：中国科学技术大学，2006.WU Ye－zhou.Feedback numbers of line graphs［D］.Hefei：University of Science and Technology of China，2006.（in Chinese）

［3］ Garey M R，Johnson D S.Computers and Intractability［M］.San Francisco：Freeman，1979.

［5］ Bafna V，Berman P，Fujito T.A 2－approximation algorithm for the undirected feedback vertex set problem ［J］.Discrete Mathematics，1999，12（3）：289－297.

［6］ Bau S，Beineke L W，Liu Z，etal.Decycling cubes and grids［J］.Utilitas Mathematica，2001，59：129－137.

［7］ Bar－Yehuda R，Geiger D，Naor J S，etal.Approximation algorithms for the feedback vertex set problem with applications to constraint satisfaction and Bayesian inference ［J］.SIAM Journal on Computing，1998，27（4）：942－959.

［8］ Focardi R，Luccio F L，Peleg D.Feedback vertex set in hypercubes［J］.Information Process Letters，2000，76（1－2）：1－5.

［9］ Liang Y D.On the feedback vertex set problem in permutation graphs ［J］.Information Processing Letters，1994，52（3）：123－129.

［10］ Luccio F L.Almost exact minimum feedback vertex set in meshes and butterflies ［J］.Information Processing Letters，1998，66（2）：59－64.

［11］ Smith G W，Walford R B Jr.The identification of a minimal feedback vertex set of a directed graph［J］.IEEE Transaction on Circuits and Systems，1975，22（1）：9－15.

［12］ Wang C C，Lloyd E L，Soffa M L.Feedback vertex sets and cyclically reducible graphs［J］.Journal of the ACM，1985，32（2）：296－313.

［13］ Wang F H，Hsu C J，Tsai J C.Minimal feedback vertex sets in directed split－stars［J］.Networks，2005，45（4）：218－223.

［14］ YANG Xiao－fan，Evans D J，Megson G.The locally twisted cubes［J］.International Journal of Computer Mathematics，2005，82（4）：401－413.

［15］ Beineke L W，Vandell R C.Decycling graphs［J］.Graph Theory，1997，25（1）：59－77.

［16］ Kralovic R，Ruzicka P.Minimum feedback vertex sets in shuffle－based interconnection networks［J］.Information Processing Letters，2003，86（4）：191－196.

［17］ XU Jun－ming，WU Ye－zhou，HUANG Jia，etal.Feedback numbers of Kautz digraphs［J］.Discrete Mathematics，2007，307（13）：1589－1599.

［18］ XU Jun－ming.Topological Structure and Analysis of Interconnection Networks ［M］.London：Kluwer Academic Publishers，2001.

［19］ Riordan J.Introduction to Combinatorial Analysis［M］.Princeton：Princeton University Press，1978.