水平分布两气泡之间相互作用及摇摆对其影响的数值模拟
2014-03-20高璞珍
黄 莹,高璞珍
(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001)
在核能工程领域,两相流动现象在核动力装置中是经常发生的,气相在水中的存在形式以及运动规律是影响两相流动特性的关键所在,因此,气泡运动特性研究对涉及两相运动的核能工程领域具有重要的理论价值和实际应用意义。
近年来,随着计算机技术和数值方法的发展,数值计算越来越广泛地应用到气泡动力学的研究,文献[1-4]应用VOF 方法模拟了高压下单个气泡上升过程中的变形情况。Chen等[5]应用VOF方法模拟了单个气泡在静止水中的上升及其与气水交界面的相互作用过程。
在现有的气泡运动数值模拟中,多数是针对单个气泡运动规律的研究,对于水平分布的两个气泡间相互作用及气泡对的上升过程的模拟则较少,VOF方法在保证具有较高精度的前提下,具有较小的计算量,相较其他数值方法更易实现,其在气泡研究领域具有不可替代的作用。本文拟采用VOF 中的PLIC 界面捕捉方法,在动量控制方程中加入表面张力项,对重力作用下两个气泡的上升过程及相互作用规律进行二维数值模拟研究。
1 物理模型
1.1 几何模型
计算域为一个2D 的矩形计算区域,尺寸为40mm×80mm,在计算域中存在水平分布的两个直径为5mm、初始形状为圆形的气泡,网格为边长0.1mm 的正方形网格。入口与出口边界条件为速度入口和自由出流,本文模拟静水情况,因此将入口速度设置为0。
1.2 摇摆模型
由于实际的海洋条件较复杂,一般可绕着管道的初始平衡位置发生6 个自由度的振荡运动,包括前后摇摆、左右摇摆、上下起伏,同时由于摇摆,还会出现管道倾斜等现象。本文在进行摇摆模拟时,做了适当的简化,将摇摆模型简化为管道绕轴线做角度变化为θ=θmsin(2πt/T)(其中θm=15°,为最大摆角幅值;T=6s,为摇摆周期)的简谐摇摆,如图1所示,摇摆中心位于管道左下角,并做以下假设:平衡位置为稳态时的位置;恢复力由波浪提供;摇摆时只发生角位移。此假设下,管道的位移角、角速度、角加速度均呈正弦规律变化[6]。
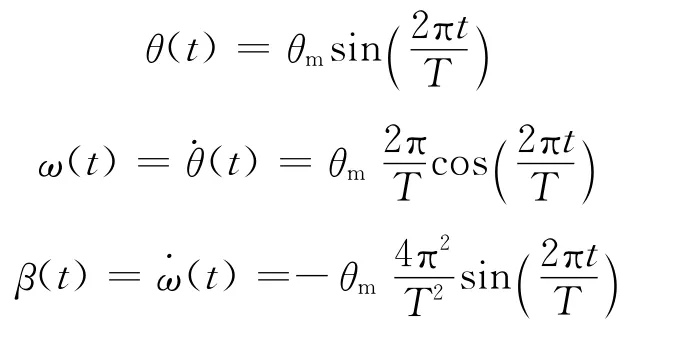
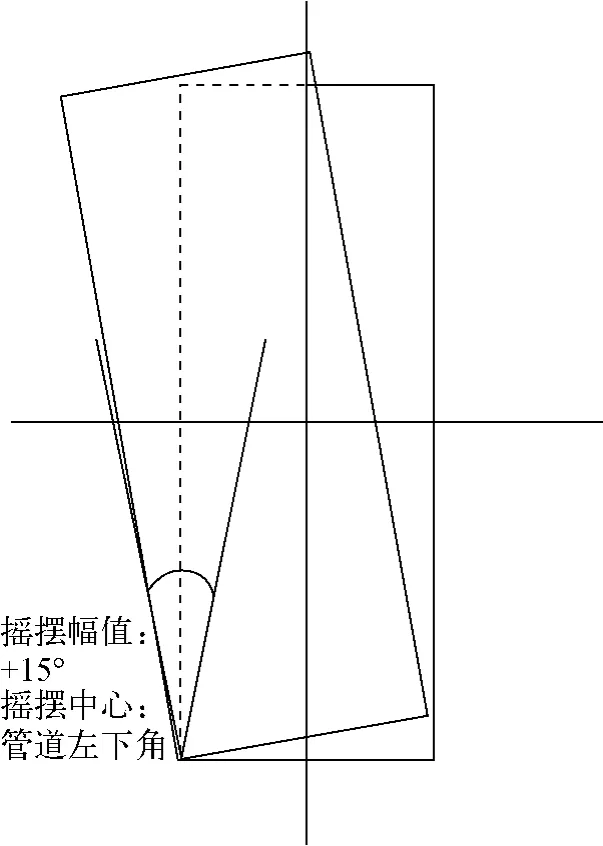
图1 摇摆示意图Fig.1 Swing diagram
2 数学模型
本文基于Fluent平台,采用VOF 模型及PLIC界面捕捉方法,结合考虑了表面张力的动量方程,对静水及摇摆情况下的气泡间相互作用特性进行数值模拟,其基本数学模型构想如下。
2.1 VOF模型
VOF方法的基本原理是通过研究网格单元中流体和网格体积比函数来确定自由界面,追踪流体的变化,而非追踪自由界面上质点的运动,在每个控制体积内,两相的体积分数之和为1。在单元中,如果第n相流体的体积分数记为αn,那么就会出现下面3个可能的情况:αn=0,第n相流体在单元中是空的;αn=1,第n相流体在单元中是充满的;0<αn<1,单元中包含了第n 相流体和其他1相或多相流体的界面[7]。
气体体积分数方程为:
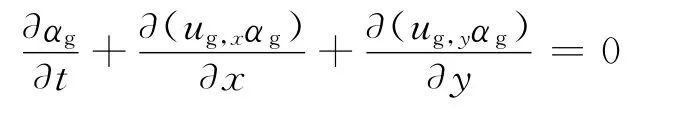
液相体积分数方程与气相体积分数方程具有相同的形式,且两相体积分数满足如下关系:
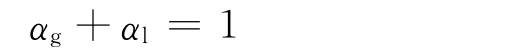
其中:αg和αl分别为气相和液相的体积分数;下标l和g分别代表液相和气相。不可压缩流体的连续方程为:

其中,u为流体速度,m/s。
考虑表面张力的动量方程为:
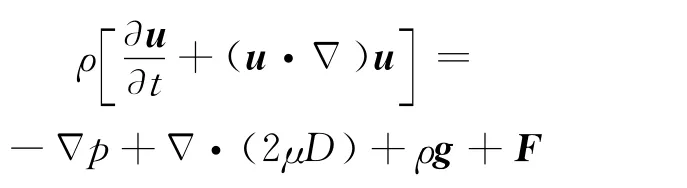
其中:ρ为两相平均密度,kg/m3;p 为压力,N;μ 为两相平均动力黏度,Pa·s;D 为应力张量,满足如下关系:
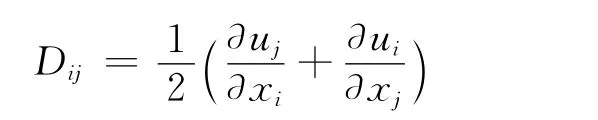
F 为由附加的表面张力导致的动量源项,具有如下形式:
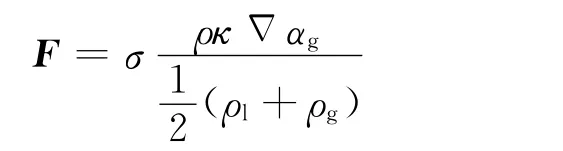
其中:κ为界面曲率;σ为表面张力系数,N/m。
出现在输运方程中的属性是由存在于每一控制体体积中的分相决定的,即:
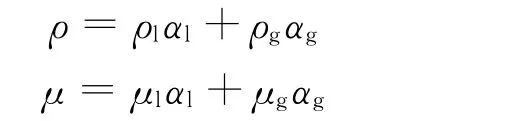
2.2 动网格模型
本文通过UDF 编程手段,在动网格模型下实现摇摆工况的模拟,在计算过程中,除了要考虑流体自身的运动,还需附加上边界的运动,这使得其控制方程会与其他情况有一定的区别。动网格模型中,在任一控制体V 内,其边界是运动的,动量方程[8]为:
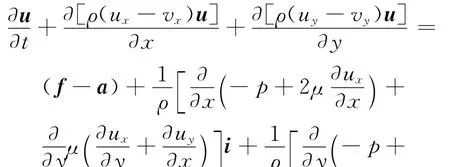
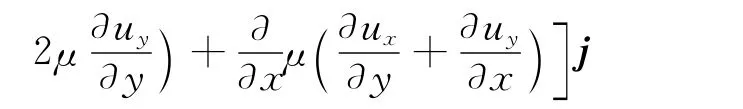
其中:vx、vy分别为控制体沿x 轴及y 轴方向的运动速度,m/s;a 为 控制体加速度,m/s2;f 为作用在单位质量流体上的质量力,N。
3 结果与讨论
3.1 上升过程气泡之间的相互作用
在一个40 mm×100 mm 的通道内(介质为水),距容器底部5mm 处水平并排分布两个直径为5mm 的球形气泡,两气泡中心的初始水平距离为5mm。模拟中液体与气体的物性参数列于表1。
当两个气泡一起运动时,由于彼此的影响,其运动特性较单气泡情况有一定的区别,如当两气泡距离较近时,其周围的流场结构会发生变化,其形状及上升轨迹等都会随之改变,且气泡之间还可能发生碰撞、聚合等情况。
气泡对水的扰动有一定的影响范围,只有气泡位于另一气泡的影响范围之内,才会产生相互作用。在作用过程中发现,气泡首先会有一相互吸引的趋势,然后又会发生分离,过程中气泡之间存在一最小距离,若初始两气泡的间距很小,即小于此最小距离时,气泡会发生接触,进行融合。本文只针对水平分布的两个气泡在静水中上升过程展现的运动特性进行研究,不考虑碰撞及聚合过程。
图2为两气泡的变形过程及周围的流场结构。可观察到,两气泡在运动过程中会使原本静止的水产生流动,形成对称分布的流场,通常表现为气泡底部存在一个射流,在气泡两侧均会有一个近似于圆形的流场结构,且两侧流场的旋转方向相反,气泡左侧周围流体逆时针旋转,右侧周围流体顺时针旋转。
在两气泡之间区域,两气泡产生的流场的水平分速度方向是相反的,速度叠加后,气泡底部射流对气泡的作用点会向叠加区域移动;气泡位于此区域的部分受到的射流推力较大,上升速度较快,气泡因两侧受力不平衡而发生旋转,两气泡呈“八”字形分布(图2d)。气泡逐渐远离,彼此之间的影响变小,气泡之间区域内两气泡所产生的流场的水平分速度相互抵消效应变小,射流对气泡的作用点向气泡中心移动(图2e)。此时,两气泡靠近壁面侧滞后,处于水中压力较大的位置,此处的空气会向气泡内的低压区移动,一段时间后,两气泡形状及位置均处于近似对称状态(图2f)。在气泡位置由倾斜达到平衡的过程中,气泡靠近壁面侧部分的速度较快,使得气泡两侧周围水的速度有所提高,气泡外侧的速度大于位于叠加区域的部分,两气泡在相互靠近的同时会呈现反“八”字形分布(图2g),气泡的形状及位置再次变得不平衡。此时气泡间距离较近,中间区域流场叠加明显,气泡尾部射流对气泡的作用点再次向叠加区域移动,气泡位于叠加区域的部分因水流的推力作用,速度逐渐变大,气泡形状及位置再次达到平衡,上述过程构成了一个位置变化周期。

表1 初始物性参数Table 1 Initial physical parameters
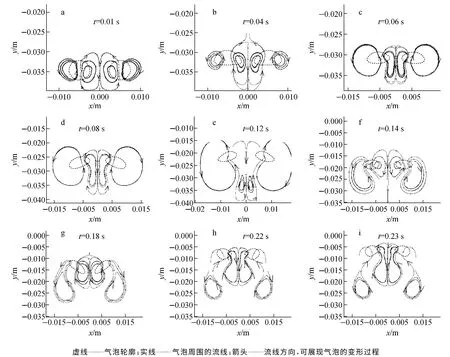
图2 两气泡周围流线分布及变形过程Fig.2 Streamline shape and deformation process of two rising bubbles
图3为两气泡上升过程的速度分布情况,可看出,初始时,气泡相互影响较弱,随着形状逐渐变得扁平,两者之间距离变小,相互影响变强,如图3b所示,两气泡之间区域流体下降速度大于另外两侧,从而产生一个低压区,两气泡会向低压区域靠近,两气泡相互吸引。当两气泡呈“八”字形分布时,二者距离逐渐变大,如图3d所示,两气泡流体速度变小,低压区域消失,从而两气泡吸引作用变弱,气泡在射流推力下逐渐分离。当两气泡由“八”字形分布恢复到平衡位置时,如图3f、g所示,气泡间流体速度变大,气泡相互吸引,两气泡再次靠近。

图3 两气泡上升过程速度分布Fig.3 Velocity distribution of two rising bubbles
上升过程中,两气泡会出现靠近-分离-再靠近-再分离的运动现象,且过程中伴随着两气泡呈现“八”字形与反“八”字形循环的现象。图4a为模拟所得两气泡位置关系的变化过程,其中8组数据从下至上依次为t=0.04、0.08、0.12、0.16、0.22、0.28、0.32、0.36s时刻气泡的位置。
图4b为实验观察到的气泡运动位置变化,图4c为实验段示意图。虽然实验中气泡沿水平方向运动,但在相同的水平高度下,两气泡之间的作用可不考虑重力,可体现出两并列气泡沿同一方向运动时,其位置关系的变化规律。从图中可看出,模拟结果与实验观察到的结果一致。
由于气泡在上升过程中左右两半部分受力不一致,使得周围流体在气泡扰动后,会出现漩涡,图5为t=0.36s时管道内的流场结构。由图4a可知,在0.36s时间内,气泡的位置关系经历了两个周期,每个周期流体会产生两对漩涡。
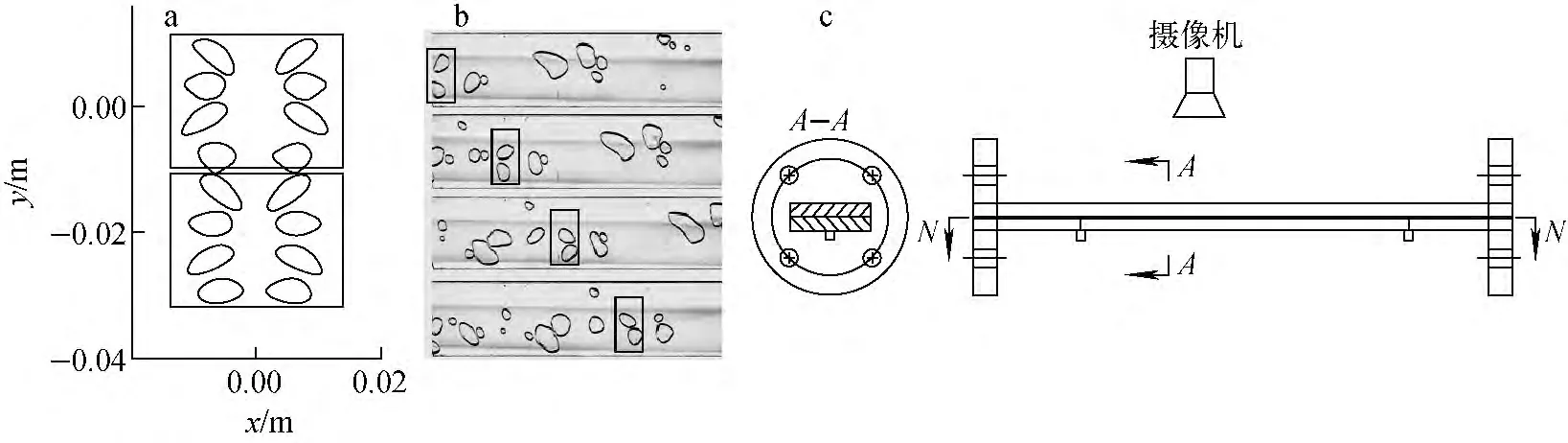
图4 两气泡同时上升运动位置周期Fig.4 Cyclicity of position relations between two rising bubbles
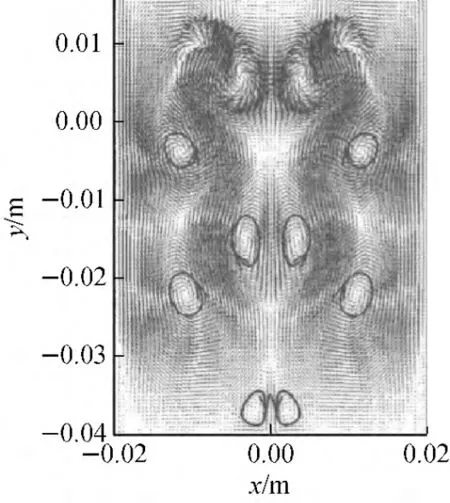
图5 气泡上升后产生的漩涡Fig.5 Vortex generated by rising bubble
3.2 摇摆对两气泡运动规律的影响
在摇摆工况下,气泡运动的独特性是由两方面因素决定的:1)气泡受到摇摆运动产生的附加惯性力的作用;2)流体随壁面摇摆运动产生的速度对气泡的影响,气泡在水中的变形过程主要受水的阻力影响。气泡间的相互作用也是通过水为介质实现的,因此,在一般情况下,后一因素的作用会明显大于前一因素的作用。
由于摇摆中心位于管道左下角,初始时,摇摆会使水具有向左上方流动的速度,从而影响气泡上升所引起的对流,使气泡周围的流场与非摇摆情况不同。摇摆会改变管道内流体原有的速度场及压力场结构,使二者均具有不对称的结构,气泡底部原本向上流动的射流在叠加了摇摆所产生的速度后,其射流方向会向通道左上方偏移,如图6所示。

图6 摇摆情况下气泡周围流线形状Fig.6 Streamline shape around two rising bubbles in swinging condition
图7为摇摆条件下气泡的变形过程,与非摇摆条件气泡的变形过程(图2)对比可看出,摇摆工况下,两气泡在上升过程中会变得更加扁平,这是因为气泡两侧的速度旋转区域内的流体受摇摆向上速度分量的影响,旋转区域会向上移动,从气泡两侧下方移至气泡两侧,流体的旋转会产生一个低压区域,这就意味着较非摇摆情况,气泡更易向两侧低压区域伸展,形状更加扁平。
从图7可发现,摇摆情况下两个水平分布的气泡由于形状变得更加扁平,两者距离会逐渐变小,所能达到的最小距离要小于非摇摆条件下的值,更容易相互影响,增大了聚合的几率,扩大了可发生聚合条件的初始距离值的范围。但在达到最小距离后,由于两者距离摇摆中心的距离不同,受摇摆影响的效果也就不同,两气泡的速度大小及方向都会有所区别,使得两气泡逐渐分开,相互作用减弱,两气泡在上升过程所展现出的周期性变化会逐渐消失。但在摇摆运动初期,两气泡仍可展现出周期性的位置关系变化过程。

图7 摇摆情况下水平分布两气泡上升的变形过程Fig.7 Deformation process of two rising bubbles in swinging condition
4 结论
1)两个水平并列分布的气泡在上升过程会出现靠近-远离-再靠近-再远离的运动现象,且二者的位置关系会呈现“八”字形与反“八”字形循环变化,模拟得到的结果与实验观察到的现象符合良好。
2)两气泡并列上升时,每个气泡都呈上下摆动状上升,气泡摆动使周围水产生漩涡,在气泡位置关系变化的一个周期内,两气泡尾部会出现两对漩涡。
3)摇摆会使气泡周围的流场结构变得不对称,气泡上升过程中变形过程更加明显,气泡变得更加扁平,两气泡所能达到的最小距离变小,但两气泡受摇摆影响不同,两气泡会逐渐分开,摇摆会破坏两气泡上升过程位置关系所展现出的周期性。
[1] LI Yong,ZHANG Jianping,FAN Liangshi.Discrete-phase simulation of single bubble rise behavior at elevated pressures in a bubble column[J].Chemical Engineering Science,2000,55(20):4 597-4 609.
[2] LI Y,ZHANG J P,FAN L S.Numerical studies of bubble dynamics in gas-liquid-solid fluidization at high pressures[J].Power Technology,2001,116(2):246-260.
[3] YANG G Q,DU Bing,FAN L S.Bubble formation and dynamics in gas-liquid-solid fluidization:A review[J].Chemical Engineering Science,2007,62(1):2-27.
[4] ZHANG Jianping,LI Yong,FAN Liangshi.Numerical studies of bubble and particle dynamics in a three-phase fluidized bed at elevated pressures[J].Powder Technology,2000,112(1):46-56.
[5] CHEN L,LI Y.A numerical method for twophase flows with an interface[J].Environmental Model and Software,1998,13(3-4):247-255.
[6] 高璞珍,庞凤阁,王兆祥.核动力装置一回路冷却剂受海洋条件影响的数学模型[J].哈尔滨工程大学学报,1997,18(1):24-27.GAO Puzhen,PANG Fengge,WANG Zhaoxiang.Mathematical model of primary coolant in nuclear power plant influenced by ocean conditions[J].Journal of Harbin Engineering University,1997,18(1):24-27(in Chinese).
[7] 江帆,黄鹏.Fluent高级应用与实例分析[M].北京:清华大学出版社,2010:32-35,140-182.
[8] 孔珑.工程流体力学[M].3版.北京:中国电力出版社,2008:225-230.
