AP1000次级汽水分离器分离性能及结构优化的数值研究

张 璜，薄涵亮

（清华大学 核能与新能源技术研究院，北京 100084）

AP1000 是美国西屋公司研发的具有非能动安全特性的第三代核电技术，目前在我国被广泛推广。AP1000 核电站采用立式蒸汽发生器，在其上部放置汽水分离装置。汽水分离装置的主要作用是将蒸汽发生器产生的湿饱和蒸汽流进行干燥。欧美各国规定经汽水分离装置干燥后的蒸汽湿度要小于0.1%，否则夹带着大量液滴的高速蒸汽流会造成二回路管道、关闭件腐蚀，以及汽轮机的汽蚀，影响汽轮机寿命［1］。同时，汽水分离装置必须尽量减小流动阻力以提高循环倍率［2］。因此，汽水分离装置的性能关系到AP1000核电系统运行的经济性和安全性。

AP1000核电站的汽水分离装置有3 部分：初级旋叶式汽水分离器、重力分离空间和次级波纹板式汽水分离器。李亚洲［3］对旋叶式汽水分离器的分离效率和流动阻力进行了实验和数值研究，得到一系列分离性能的实验数据和内部流场可视化结果。张谨奕等［4］通过建立重力分离空间内单个液滴的运动模型，系统地研究了重力分离空间的分离机理。然而由于AP1000 次级波纹板式汽水分离器结构特殊，至今尚无学者对其分离性能做较为深入的研究。

AP1000次级分离器为带钩型波纹板，它的内部流场为气液两相流，其中连续相为饱和蒸汽，离散相为饱和水滴。由于两相流动的复杂性，理论研究一般难于进行。同时由于实际工况下波纹板内部压力和温度较高，实验研究也难于开展。因此本文采用数值模拟方法研究实际工况下波纹板的分离性能。首先分析AP1000 波纹板内部两相流动特点并建立两相流动模型；其次对该模型数值求解，得到波纹板内部气相流场中不同粒径液滴的轨迹和液滴湿度分布，从而得到波纹板流动压降和分离效率；最后以已采用的数值研究方法为基础，根据提高分离效率和降低流动压降两个目标，对AP1000波纹板内部结构进行优化。

1 理论模型

1.1 物理描述

AP1000次级分离器为带钩型波纹板（图1）。实际工况下波纹板内部为气液两相流动，一般假设为二维流动。其中气相为连续状态的饱和水蒸汽，液相为离散状态的饱和水滴。实际工作压强为5.764 MPa，温度为273 ℃。波纹板入口的蒸汽湿度在2%左右［2］，此时液滴相的体积份额αd约为8×10-4，因此认为液滴相是稀疏相，所以不考虑液滴对气相动量的影响，同时也可忽略液滴之间的碰撞效应［5］。由于气液两相处于饱和状态，故本文假设两相之间无质量和能量交换。液滴的直径远小于波纹板的特征尺寸，因此可将其视为刚性小球而不考虑它在运动过程中的形变。

蒸汽从波纹板进口流入出口流出会产生流动压降。液滴受到流场的作用力和力矩，导致它们的平动速度、转动角速度和位移时刻都在变化。液滴如果撞击上波纹板壁面即被分离［2］；液滴如果最终流出波纹板，则会随蒸汽一起进入蒸发器顶部的节流器。由于进入波纹板的液滴数目巨大，如果对每个液滴进行跟踪，将会消耗大量的计算时间，因此本文选取特征液滴代表真实液滴。

设X、V 和R 分别表示液滴的位置、速度和半径空间，三者构成相空间｛X，V，R｝。相空间中特征液滴的物理意义为：在相空间点（X′，V′，R′）附近的液滴，如果它们的位置、速度和半径可用某一平均值（X″，V″，R″）表示，那么具有（X″，V″，R″）值的液滴就称为特征液滴。如果将相空间用坐标表示（图2），相空间点为（X′，V′，R′）（箭头所指位置），空心圆代表其附近液滴，实心圆代表特征液滴且位于相空间点（X″，V″，R″）处。特征液滴仅是一组单个液滴的代表，所以其运动规律和单个液滴在流场中的运动规律相同。基于本节前段对波纹板内部两相流动的物理描述，本文对特征液滴的运动和其背景蒸汽流场提出如下假设：1）特征液滴运动的背景蒸汽流场是稳态的；2）流场和特征液滴之间处于热力学平衡态；3）特征液滴为刚性圆球；4）特征液滴的运动可分解为空间平移与空间旋转的叠加；5）流场对特征液滴具有作用力而特征液滴的形状、大小和运动对流场无影响；6）特征液滴的运动速度与当地流场速度相互独立且存在差异；7）特征液滴之间不发生碰撞、聚合等过程。

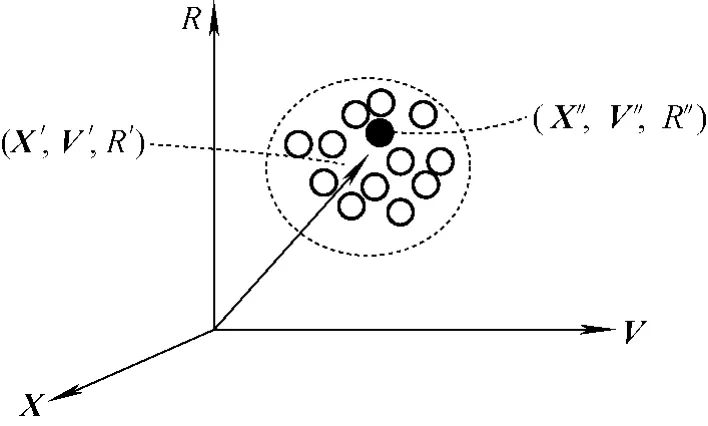
图2 特征液滴的示意图Fig.2 Schematic diagram of characteristic droplet

1.2 特征液滴的选取

要模拟特征液滴每时每刻的运动状态（平动速度、转动角速度和位移），必须知道特征液滴的初始信息。初始时刻，设全空间内真实液滴总数为nsym，该值用Dirac-δ 函数（简记为δ函数）表示为：

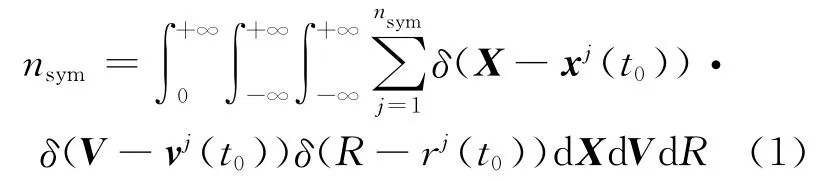
其中，xj（t0）、vj（t0）、rj（t0）分别表示nsym个真实液滴中第j个液滴的初始位置、速度和半径，简记为

如果将空间位置X、速度空间V 和半径空间R 分别划分为NX、NV和NR组，每组间距分别为ΔX、ΔV 和ΔR，则初始真实液滴共划分为Nrep组：

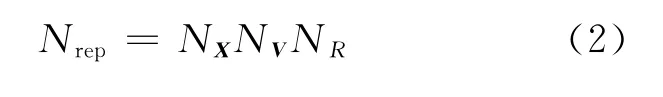
设第K 组真实液滴的总数为nK，用1个特征液滴表征该组真实液滴的运动状态，令=（，，）′表示第K 组特征液滴的初始状态，并使其满足下式：

根据式（2），可选取Nrep个特征液滴，其初始状态Y0为：

每组特征液滴的数目相应为n1，…，nK，…，nNrep。因而初始时刻所有真实液滴的状态信息，全部转化成离散变量Y0。

1.3 两相流动的数学模型

蒸汽相运动采用Euler坐标系描述，蒸汽的速度和压强为Euler变量X 和t 的函数，即u=u（X，t），p=p（X，t）。假设蒸汽为不可压缩牛顿型流体，考虑稳态情形，连续性方程和动量方程为：

其 中：ρf 为 流 体 密 度；g 为 重 力 加 速 度；ν为 流 体运动黏性系数。

特征液滴的运动采用Lagrange观点描述，其各时刻的位置x（x0，t）称作Lagrange变量。特征液滴的运动规律满足张谨奕等［6］提出的Z＆B模型。

设t时刻所有特征液滴的状态为Y（t）：

Z＆B模型中，特征液滴的半径不随时间变化，但需考虑特征液滴角速度的变化，因而有：

其中：y（t）K为t时刻第K 组特征液滴的状态；x（t）K、ω（t）K和v（t）K分别为t 时刻特征液滴的空间位置、角速度和速度。以下为表达简洁，将y（t）K、x（t）K、ω（t）K和v（t）K分别简记为y（t）、x（t）、ω（t）和v（t）。所有特征液滴的状态Y（t）满足方程：

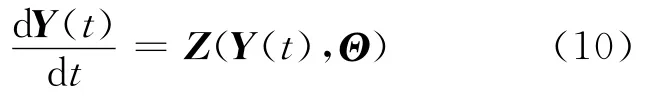
其中，Θ 为与所有特征液滴运动相关的参数。

对于式（8）的第K 个分量y（t），满足方程：

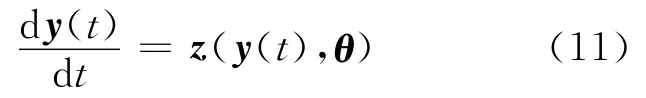
其中，θ 为与第K 组特征液滴运动相关的参数。

y（t）共有3个分量x（t）、ω（t）和v（t），记为：

x（t）满足的方程为：

ω（t）满足的方程为：

其中：I=2mr2／5 为 第K 组 特 征 液 滴 转 动 惯量，r为液滴半径，m 为第K 组特征液滴质量；M=-0.5ρfCMr5|ω-Ω／2|（ω-Ω／2）为第K组特征液滴所受合力矩，CM为转矩系数，流场旋度Ω=Δ×u。

v（t）满足的方程为：

其中：m=4πρdr3／3，ρd 为液滴密度；曵力FD=πCDρf|u-v|（u-v）r2／4，CD为曵力系数；惯性质量力FA=2πρfr3［d（u-v）／dt］／3；体积力FV=4πr3（ρd-ρf）g／3；Magnus升力FM=πCMaρfr3·（u-v）×（ω-Ω／2），CMa为Magnus升力系数；Saffman升力FS=6.46CSa（Rμ）2（ρfμf）0.5r2|Ω|-0.5·［（u-v）×Ω］，CSa为Saffman升力系数，（Rμ）2表示特征液滴内部环流量对升力的影响，μf 为流体动力黏性系数。

将以上各表达式代入式（13）～（15），并将方程左边系数归一化得：

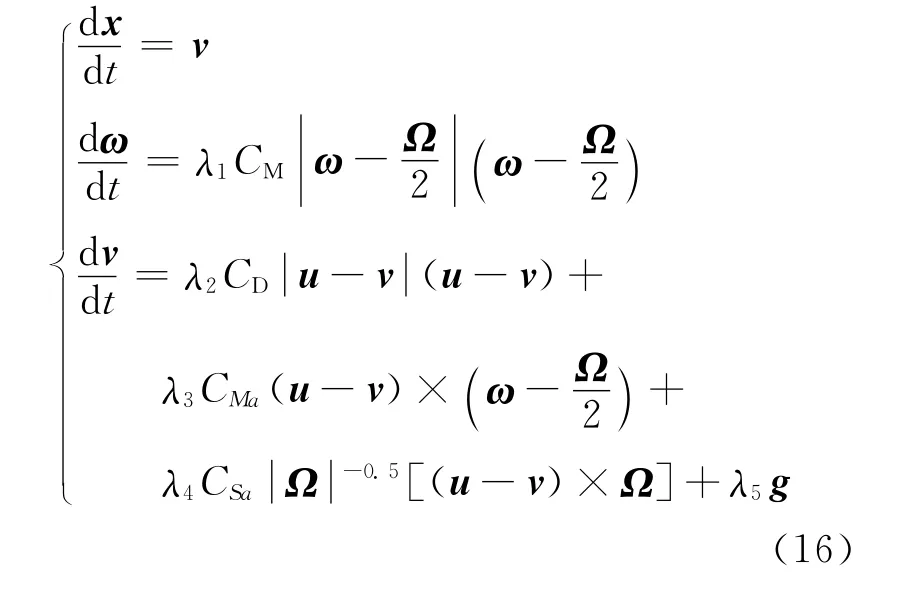
其中：λ1=-15ρf／16πρd、λ2=3ρf／（8ρdr+4ρfr）、λ3=3ρf／（4ρd+2ρf）、λ4=［1.615（μd+2μf／3）2／（μd+μf）2（μfρf）0.5］／（ρdπr／3+ρfπr／6）、λ5=2（ρd-ρf）／（2ρd+ρf）为 归 一 化 系 数；CM、CD、CMa、CSa等系数的值详见文献［6］。

式（16）中u和Ω 由式（6）和（7）确定，故该式封闭。且该式的初值为式（4），因而式（16）是给定初值的常微分方程组。因此要确定Nrep个特征液滴在t时刻的状态Y（t），需要求解式（10）的Nrep个分量方程，进而需要求解Nrep个式（11）。而式（11）又有3个分量，每个分量的方程为式（16）。故同时求解这3 Nrep个方程就能得到所有特征液滴在t时刻的状态Y（t）。

1.4 液滴湿度的计算

利用1.2和1.3节中的理论模型，可给出流场内液滴湿度分布的计算方法。设用网格对全空间进行离散后，第m 个网格的特征位置为Xm（可取网格的重心位置）。在t时刻，第m 个网格内（即ΔXm内），速度空间VΔV 及半径空间RΔR 内的液滴数目nΔ为：

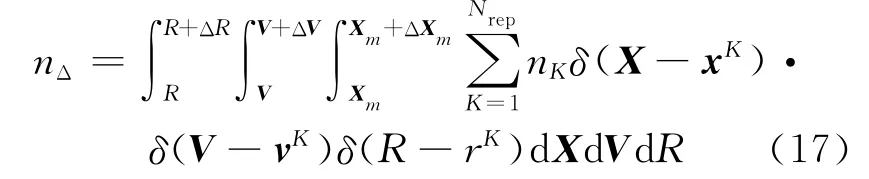
式（17）用数目密度函数f（X，V，R，t）表示为：

由式（17）、（18）可得：

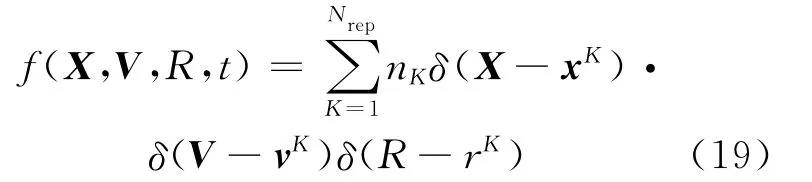
其中，xK、vK和rK均 可 由1.3 节 所 述 方 法 求出。因此，通过式（19）可将已知的xK、vK和rK转变成f（X，V，R，t）。那么t时刻，第m 个网格内液滴的体积份额αm和湿度βm 为：

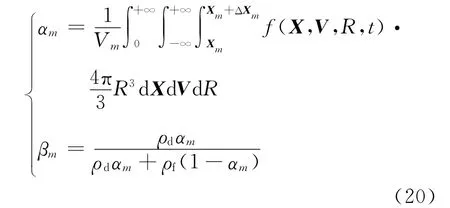
其中，Vm为第m 个网格的体积。

2 数值求解

2.1 蒸汽流场求解

蒸汽流场通过ANSYS Fluent 13 求解。首先用ANSYS ICEM 13对波纹板划分网格。由于波纹板壁面带钩，故采用四边形-三角形混合型网格。其次将生成的网格文件导入ANSYS Fluent 13中计算流场。物性参数ρf=29.51kg／m3，μf=1.84×10-5Pa·s，入口速度为2.05 m／s［7］，雷诺数约为76 000，故蒸汽流动为湍流，本文选择SSTk-ω 模型，并附加低雷诺数修正。波纹板壁面设为无滑移边界，出口设为压力边界。为保证解有足够精度，压力项和动量项采用二阶迎风格式，连续性方程的残差设为5×10-4，其余各项残差设为10-5。对同一套网格，需做网格自适应，使监测点的数据不发生变化，同时保证壁面处的y+小于5［8］（SSTk-ω 模型不采用壁面函数而是用低雷诺数修正）。最后需计算不同疏密的多套网格得到网格独立解。

2.2 特征液滴运动状态求解

液滴物性参数ρd=762.43kg／m3和μd=9.63×10-5Pa·s。由2.1节求得蒸汽流场各位置的速度和旋度，使之封闭单个特征液滴运动方程，即式（16）。该式为非线性常微分方程组，初值条件为式（4）。由于式（16）中等式右边项的刚性很大，故根据数值稳定性条件，选取算子分裂算法或经典Runge-Kutta算法求解该式［9］。特征液滴运动状态的求解程序为自编程序，该程序可与Fluent软件耦合。

3 模拟结果

AP1000波纹板（一型波纹板）内部静压场和速度矢量场的模拟结果示于图3。由图3a可知，一型波纹板入口静压高，出口静压低。由图3b可知，入口速度低，出口速度高。由于钩的存在，其附近会形成大小不等的漩涡。计算得到波纹板进出口的总压降为1 558Pa。

特征液滴（以下如无特别说明，简称液滴）在波纹板入口处均匀分布，液滴入射速度与蒸汽流 速 相 同［10］，液 滴 直 径 为2～70 μm［11］。图4为不同直径液滴在一型波纹板内的轨迹。由该图可见，直径越小的液滴，越易随蒸汽流出波纹板；直径越大的液滴，越易与波纹板的钩或壁面碰撞，从而被分离去除。

波纹板的分离效率ηeff定义如下：

其中，min、mout分别为进入和流出波纹板的真实液滴总质量。进入波纹板的真实液滴数目nsym是定值，选取Nrep组特征液滴代表真实液滴，而Nrep的大小可根据计算精度调整。这里以分离效率作指标，逐渐增大Nrep值，当计算所得的分离效率值恰好不再变化时，取此时的Nrep值为最终特征液滴数目。经数值实验确定Nrep值为100。

由于在流场内部，液滴湿度小于1，且最小和最大值往往相差几个数量级，为使液滴湿度分布图经由Tecplot 360软件处理后有更好的对比度，将每个网格内的液滴湿度进行如下变换：

其中，β′m为经变换后得到网格内的等效湿度。易知β′m与βm 正相关，即β′m越大表明βm 越大，反之亦然。图5为稳态情况下不同直径液滴在一型波纹板内的等效湿度分布。对比图4、5可看出，图4中液滴轨迹密集的区域，图5中液滴的湿度大。在钩附近，液滴的湿度较大，说明有部分液滴撞击到钩上，或一直在附近的漩涡内运动。

图3 一型波纹板内部静压场（a）和速度矢量场（b）的模拟结果Fig.3 Numerical results of static pressure field（a）and velocity vector field（b）in wave-type plate one

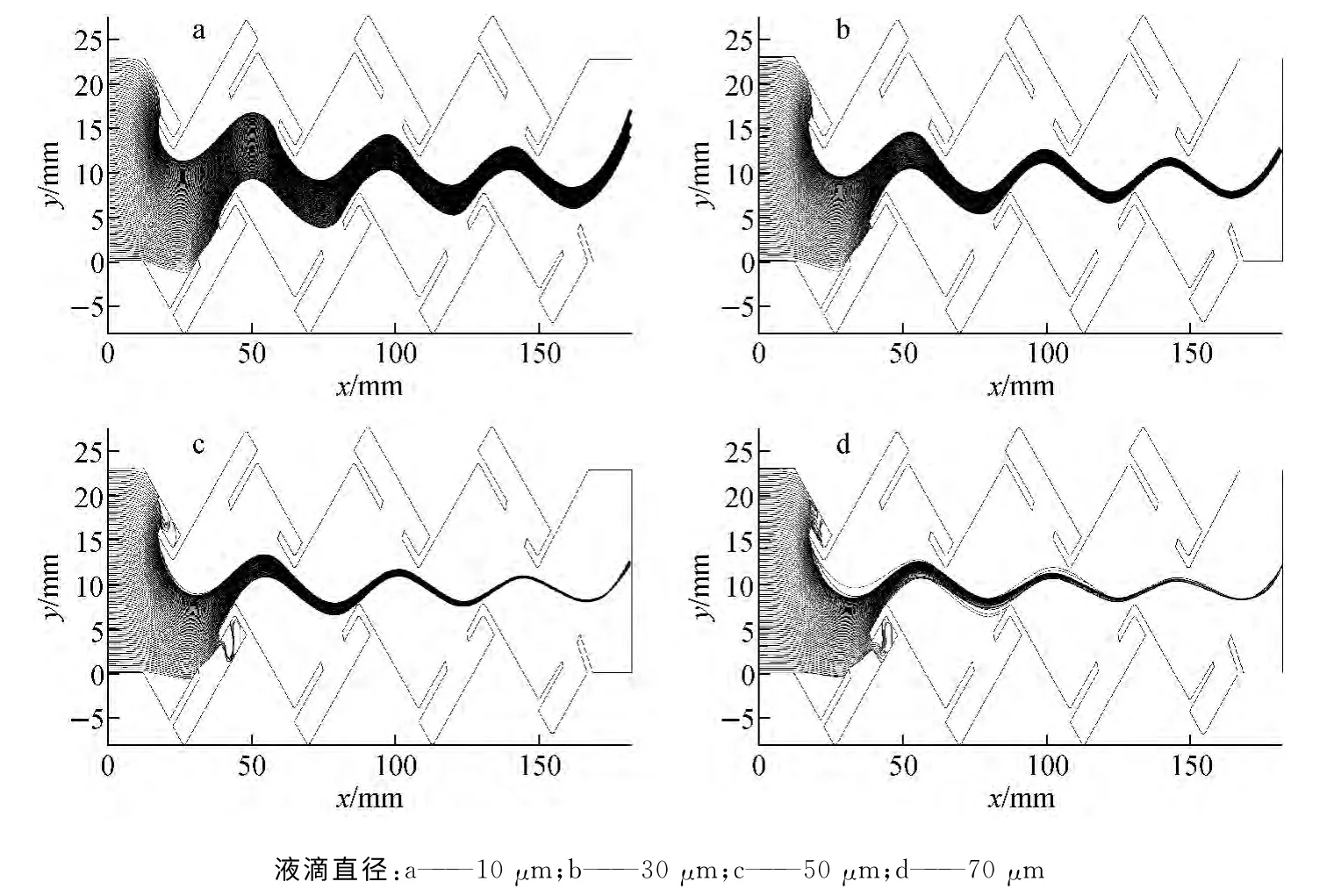
图4 不同直径液滴在一型波纹板内部的轨迹Fig.4 Trajectories of droplets with different diameters in wave-type plate one

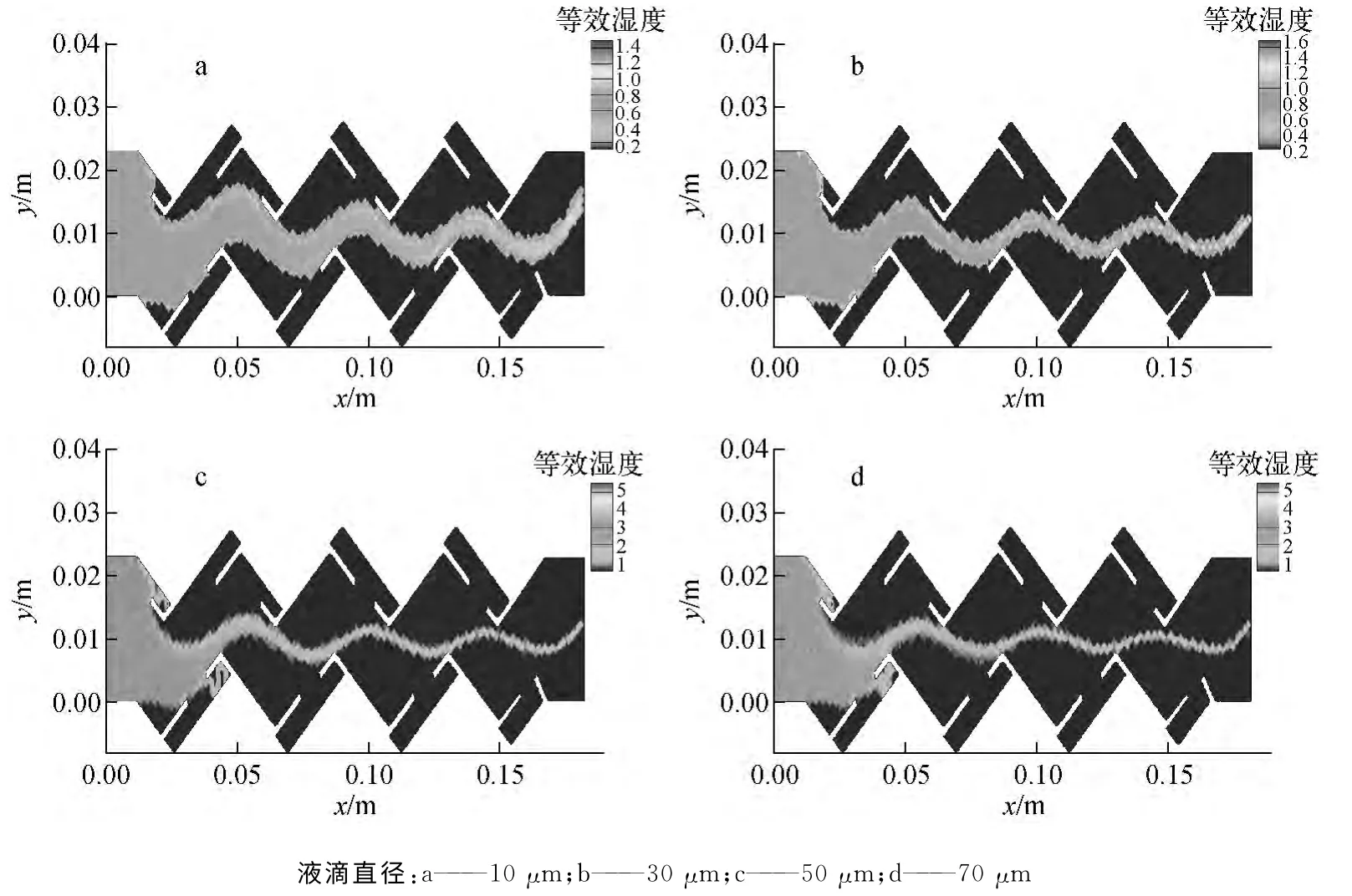
图5 不同直径液滴在一型波纹板内部的等效湿度分布Fig.5 Equivalent moisture distribution of droplets with different diameters in wave-type plate one

图6为一型波纹板对不同直径液滴的分离效率。由该图可知，一型波纹板的分离效率并不理想，因为对于直径为5μm 左右的液滴，分离效率几乎为0。虽然随液滴直径的增大，分离效率有所提高，但是分离效率依然不到50%。因此，有必要优化一型波纹板的结构以提高其分离效率。

图6 一型波纹板对不同直径液滴的分离效率Fig.6 Separation efficiency of droplets with different diameters in wave-type plate one

4 优化方案

由图4、5可见，一型波纹板的钩可阻挡液滴，且液滴的轨迹也在钩的附近。因此本文通过改变钩的形状来优化波纹板结构。图7为4种不同的优化方案。其中二型波纹板将一型中下壁面上的弯钩变为直钩；三型波纹板将一型中上壁面的弯钩变为直钩；四型波纹板只将一型中前两个弯钩变为直钩；五型波纹板将一型中前两个弯钩变为直钩，同时去掉其他钩。

图8为一型至五型波纹板对不同直径液滴的分离效率。由图8可见，二型至五型波纹板对直径大于27.5μm 的液滴的分离效率为100%，而一型波纹板对这类液滴的分离效率最大也不到50%。对于直径小于15μm 的液滴，四型波纹板的分离效率最好；对于直径在15～27.5μm 范围内的液滴，二型波纹板的分离效率最好。然而，二型至五型波纹板对直径小于27.5μm 的液滴的分离效率差别不大。可见优化后的二型至五型波纹板，其分离效率较一型均有较大提升。

图7 优化后的波纹板结构Fig.7 Structure of optimized wave-type plate

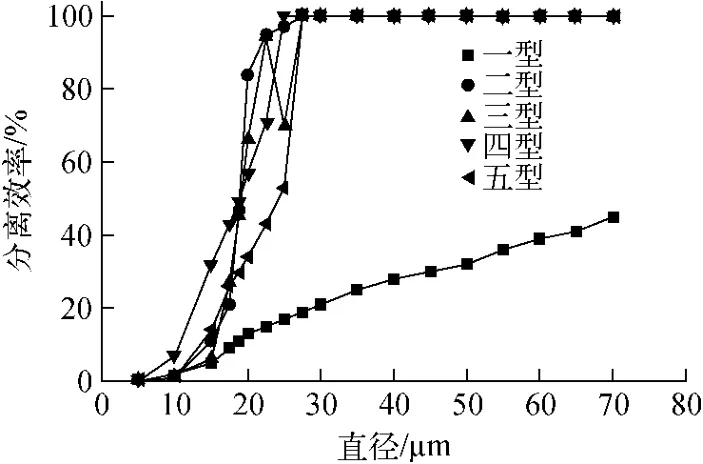
图8 一型至五型波纹板对不同直径液滴的分离效率Fig.8 Separation efficiency of droplets with different diameters in wave-type plate from type one to type five

同时波纹板的流动总压降是其结构优化的另一指标。表1列出一型至五型波纹板的进出口总压降。由图8和表1可知，虽然二型至四型波纹板的分离效率较高，但是它们的进出口总压降也较高。五型波纹板的总压降较一型的低，且其分离效率与二型至四型波纹板接近，因此五型波纹板具有高分离效率、低流动阻力的特点，所以本文选择五型波纹板作为最终优化方案。

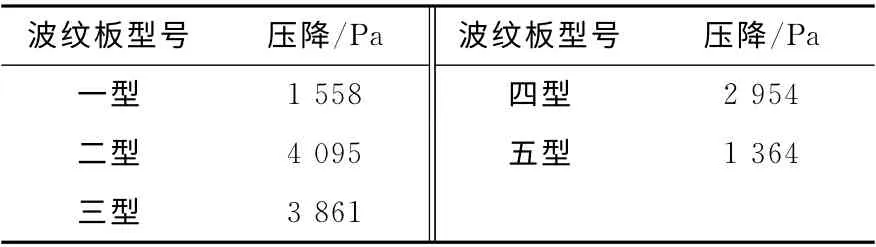
表1 不同型号波纹板进出口总压降Table 1 Total pressure drop between inlet and outlet of wave-type plate with different types

为说明五型波纹板的分离机制，将不同直径液滴在其内部的轨迹示于图9。由图9 可见，五型波纹板前端的两个直钩起到分离大部分液滴的作用。50μm 和70μm 的液滴易直接撞击到直钩被分离；30μm 的液滴绝大部分会撞击到直钩，另一部分由于惯性作用，撞击到波纹板的壁面而被分离；对于直径为10μm 的液滴，直钩对其也有一定的分离和阻挡作用。

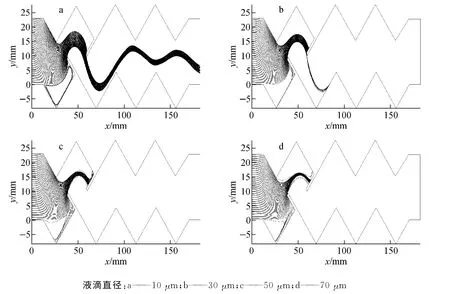
图9 不同直径液滴在五型波纹板内部的轨迹Fig.9 Trajectories of droplets with different diameters in wave-type plate five

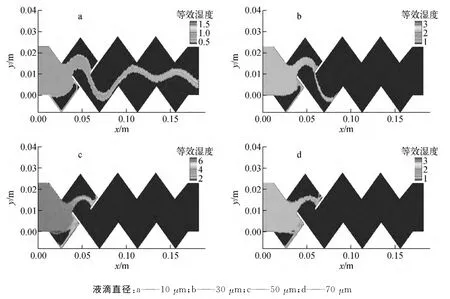
图10 不同直径液滴在五型波纹板内部的等效湿度分布Fig.10 Equivalent moisture distribution of droplets with different diameters in wave-type plate five

图10为稳态情况下五型波纹板内不同直径液滴的等效湿度分布。对比图9、10可知，图10中有液滴湿度分布的区域，在图9中就有液滴经过。图9中液滴轨迹越密集的区域，图10中液滴湿度越大。因此图10亦可说明五型波纹板的分离机理。

由图3可知，有钩处易形成漩涡。而漩涡处能量耗散大，导致总压损失大。由此推知，波纹板的钩越多，其流动阻力越高。五型波纹板仅有两个直钩，因此形成漩涡的区域少，从而总压损失小，所以流动阻力低。

综上可知，五型波纹板提高了一型波纹板的分离效率并降低了其流动阻力，达到结构优化的目的。

5 总结和展望

本文通过数值模拟的方法，研究了AP1000次级波纹板（一型波纹板）汽水分离器的分离性能，并优化其结构，使之分离性能有较大提高且流动阻力也有所降低。主要结论如下：

1）针对一型波纹板内液滴运动和蒸汽流动特点，建立了两相数学模型；

2）通过数值模拟一型波纹板内的两相流动，给出了该波纹板对不同液滴的分离效率；

3）通过优化一型波纹板结构，设计出具有高分离效率和低流动阻力的五型波纹板。

进一步的工作包括：论证是否可制造加工出五型波纹板；分析五型波纹板结构的力学特性。

［1］ GREEN S J，HETSRON G.PWR steam generators［J］.International Journal of Multiphase Flow，1995，21（Suppl.）：1-97.

［2］ 《蒸汽发生器》编写组.蒸汽发生器［M］.北京：原子能出版社，1982.

［3］ 李亚洲.旋叶汽水分离器冷态试验和数值分析研究［D］.上海：上海交通大学，2013.

［4］ 张谨奕，薄涵亮.重力分离空间均匀流中液滴行为问题研究［J］.原子能科学技术，2010，44（增刊）：293-297.ZHANG Jinyi，BO Hanliang.Investigation on droplets behavior in uniform flow of gravity separation space［J］.Atomic Energy Science and Technology，2010，44（Suppl.）：293-297（in Chinese）.

［5］ CROWE C T，SCHWARZKOPF J D，SOMMERFELD M，et al.Multiphase flows with droplets and particles［M］.Boca Raton：CRC Press，2012.

［6］ 张谨奕，薄涵亮，孙玉良，等.三维空间液滴运动模型［J］.清华大学学报：自然科学版，2013，53（1）：96-101.ZHANG Jinyi，BO Hanliang，SUN Yuliang，et al.Three-dimensional droplet motion model［J］.Journal of Tsinghua University：Science and Technology，2013，53（1）：96-101（in Chinese）.

［7］ Westinghouse proprietary class2design specification，F-3.5.5-1 Rev.1［R］.US：Westinghouse Electric Company，2013.

［8］ 张兆顺，崔桂香.流体力学［M］.2 版.北京：清华大学出版社，2006.

［9］ 张璜，薄涵亮.三维空间液滴运动模型数值解法研究［J］.原 子 能 科 学 技 术，2014，48（5）：818-826.ZHANG Huang，BO Hanliang.Study on numerical algorithm of droplet motion model in threedimensional space［J］.Atomic Energy Science and Technology，2014，48（5）：818-826（in Chinese）.

［10］李嘉.波形板汽水分离器的理论和实验研究［D］.武汉：华中科技大学，2007.

［11］GALLETTI C，BRUNAZZI E，TOGNOTTI L.A numerical model for gas flow and droplet motion in wave-plate mist eliminators with drainage channels［J］.Chemical Engineering Science，2008，63（23）：5 639-5 652.