一种基于CMAC神经网络的板形模式识别新方法

李 艳，张自立，吕建红

(1.军械工程学院信息工程系，河北石家庄 050003;2.石家庄学院计算机学院，河北石家庄 050035)

板形模式识别是冷轧带钢生产的核心。其主要 任务就是将检测到的板形应力分布离散值，经过一定的数学方法进行适当的模式分解，得到板形特征参数值，为控制系统提供控制策略。

随着板形识别和控制精度要求的提高，提出了板形模式识别的模糊分类方法和神经网络板形模式识别方法，其中应用最广的方法是神经网络方法。目前，神经网络用于板形识别的尝试是将带钢沿宽度方向所有测量区的板形缺陷值作为输入送入神经网络，输出为对应板形缺陷基本模式的隶属度。这种方法需要的输入量多，网络结构复杂，加大了网络学习的工作量，而且对于不同宽度的带钢需要不同的网络拓扑结构，因而通用性和实用性不强［1］。

为此建立了一种新的CMAC(小脑模型联接控制器)网络识别模型。该网络模型在训练中引入了动态学习率来调整权值。这种模型有效地解决了传统板形识别模型的不足。仿真结果表明，这种模型大大提高了板形识别的精度和速度。

1 基于CMAC的板形模式识别模型

1.1 板形识别的基模式

轧后板形表现为纵向残余应力δ(y)的横向分布。此残余应力满足其自相平衡的条件，即沿板宽的积分值为零，如式(1)所示。

式(1)中y为横向相对坐标，从板的一边到另一边，y从－1变化到+1。式(1)称为板形的基本性质。

由于控制方法的限制，工程上常见的板形识别信号基本模式包括左边浪、右边浪、中间浪、双边浪、右三分浪、左三分浪、四边浪、边中浪等。每一种模式所对应的残余应力仍然需要满足式(1)。对上述8种模式的残余应力分布进行归一化处理，将其定义为板形的基模式。选用一次、二次、三次、四次勒让德正交多项式表示上述4对两两互反的8种板形基模式所对应的残余应力分布［2］，如图1所示。

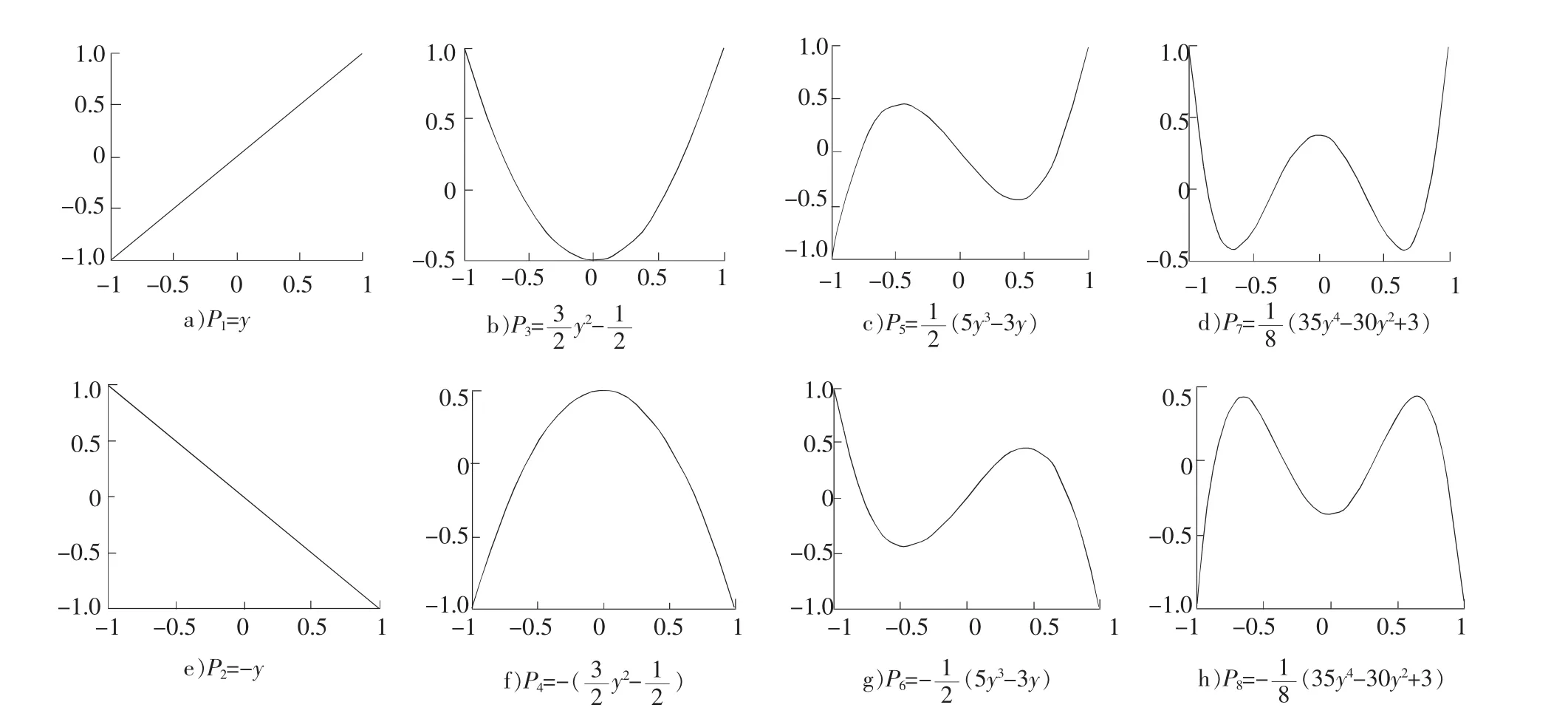
图1 板形基模式应力图Fig.1 Basic patterns of flatness

图1所示的板形基模式曲线，均满足式(1)表示的板形基本性质。所以选用勒让德正交多项式表示板形是较合理的。一般地，轧后板形可表示为基模式板形的线性组合，如式(2)所示。

其中P1，P3，P5，P7分别表示一次、二次、三次、四次勒让德正交多项式。a1，a3，a5，a7分别表示板形的线性特征系数、二次特征系数、三次特征系数和四次特征系数。

可见，板形识别实际上是经过数学运算，提取出板形的基模式系数或特征系数 a1，a3，a5，a7。由于a1，a3，a5，a7均可为正或负，故可分别表示上述8种板形基模式分量的大小。

1.2 基于CMAC网络的板形模式识别模型输入神经元的确定

传统的板形识别模型在识别板形时，直接将n个实测板形应力信号作为网络的输入，所以网络的拓扑结构是由轧件的宽度决定的。然而，对于宽带冷轧机，需要有多个不同拓扑结构的神经网络才能完成板宽变化时的识别任务。为了解决这个问题，近年来的识别模型中采用了基于欧式距离［2］的神经网络板形模式识别方法。它将待识别样本与基本模式的欧式距离作为网络的输入，则网络输入节点的数目由基本模式的数目决定。由于现阶段冷轧带钢的基本模式数目通常由实际生产决定，因此输入节点的数目是确定的，网络结构固定，较之多点板形应力信号值作为模型输入的思想，大大减少了输入节点的个数，简化了网络结构，在精度及控制的复杂程度上都取得了非常大的进展。

待识别样本y与第k个标准样本的欧式距离如式(3)所示。

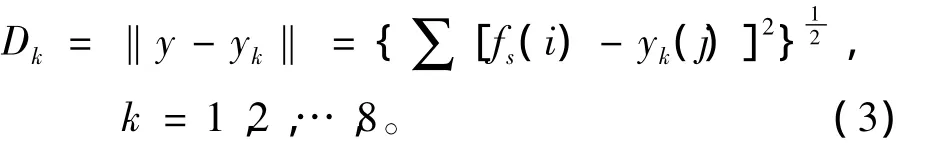
式中:y=(fs(1)，fs(2)，…，fs(n))表示实测的待识别样本归一化函数;yk=(yk(1)，yk(2)，…，yk(n))为8个标准样本归一化函数。

将Dk归一化得

DDi为待识别样本与一对互反的基本模式之间的欧式距离的差，如式(5)所示。

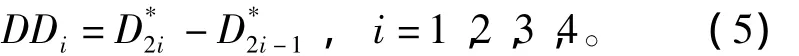
1.3 CMAC网络模型输出神经元的设置

板形缺陷的8种基本模式中包括4对两两互反的模式，根据轧制过程中轧件板形的实际情况，识别出的板形基本模式中互反的2种模式不能同时存在，因此CMAC神经网络的输出层采用4个输出节点就可以准确地表达出各种基本模式的隶属度。当输出值为正数时，分别表示左边浪、中浪、右三分浪和正四分浪;当为负数时，分别代表的则是右边浪、双边浪、左三分浪和反四分浪。

1.4 CMAC板形识别模型

小脑模型联接控制器CMAC神经网络是1972年由ALBUS提出的［4］。它是一种具有局部学习能力的前馈神经网络，其结构简单、学习速度快，具有一定的泛化性等特点，能较好地完成非线性映射。CMAC神经网络的基本思想在于学习系统特征的近似值，然后产生合适的控制信号［5］。CMAC神经网络已经被成功的应用在很多领域，比如机器人控制、信号处理、模式识别等。

为了提高板形识别的精度和速度，本文提出了一种CMAC板形模式识别模型。本识别模型利用欧式距离差作为网络的输入，各种基本模式的隶属度作为网络的输出，是一种4输入4输出的识别模型。这种CMAC神经网络识别模型是一种联想存储网络。其传输函数类似于一种查表函数。本模型是一种两层联想神经网络模型［6］，其包括两个基本的映射函数X→A和A→Ap。CMAC板形识别模型的结构如图2所示。

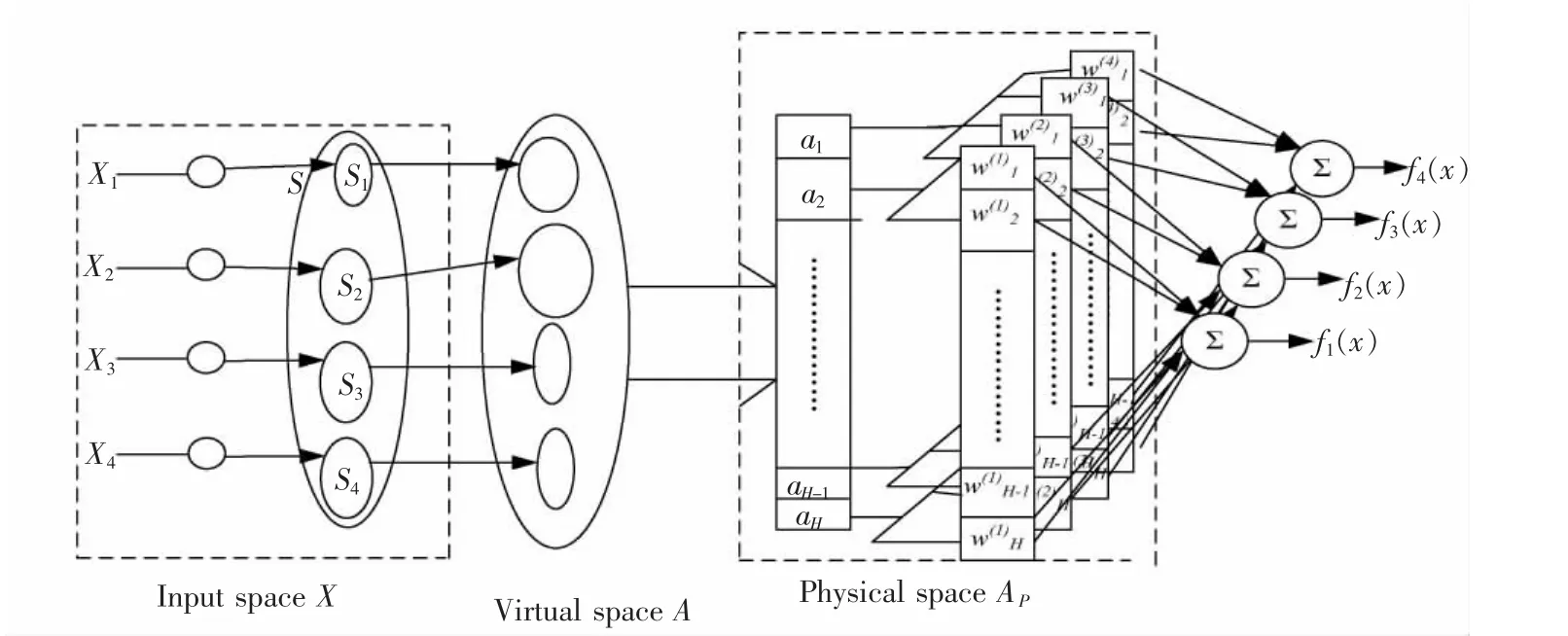
图2 CMAC板形模式识别模型结构Fig.2 Structure of CMAC flatness recognition model

对于映射X→A，输入空间X中的每个细胞单元首先被量化，然后分别与虚拟空间A中相对的项相联合。在大多数多输入的情况下，由于A会变得很大，因而不能实现网络的功能［7-9］。因此为了压缩虚拟空间A到一个较小的物理空间Ap，实现映射A→Ap，模型采用了哈希代码［10-13］。

在整个映射过程中，输入量x首先被量化到S，其量化数为R，Si是输入量被量化的R维的量化参数。然后在物理空间Ap中，由映射得到一组相适应的权值wi(i=1，2，…，H)。CMAC网络的输出如式(6)所示，其中fi(x)表示输出变量。

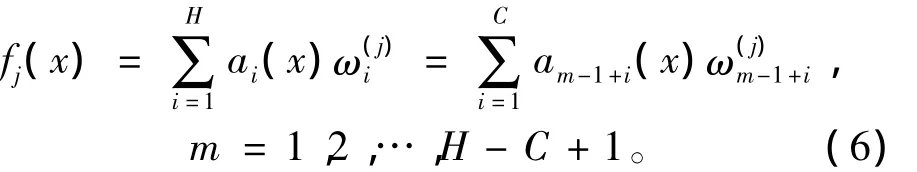
式中:fj(x)是第j个实际输出;x为n维的输入量;a为H维被激活的单元;C为量化参数，其表示每维输入空间中被激活的单元数;m为被激活的存储单元的首地址;ω(j)i表示第j个输出的第i个存储单元中的权值。

CMAC网络运用误差校正算法。其计算量小、收敛速度快。根据Widrow-Hoff规则，CMAC网络的学习算法表示如下。

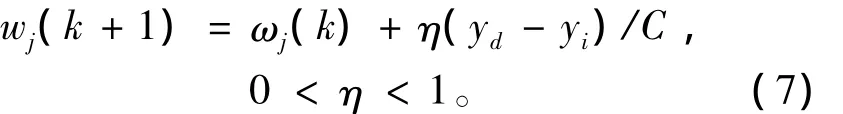
式中:k为CMAC的迭代步数;η为学习率;yd为期望输出;(yd－yi)为训练的误差样本。

1.5 CMAC模型的改进算法

CMAC网络模型的学习率在其权值更新中起着重要的作用［14］。传统的CMAC神经网络具有固定的学习率，这是不合理的。若使CMAC有较大的学习率，其学习速度越快，然而其学习误差就会更大，并且引起网络的不稳定。相反，有较小学习率的CMAC网络其训练误差较小，结果较准确，然而其学习速度较低。因此，CMAC模型中应引入动态学习率。为了获得动态学习率，本文采用了标准误差函数。根据此函数，动态学习率通过误差收敛获得。网络模型通过变化的学习率，更新相应的权值。标准误差函数见式(8)。

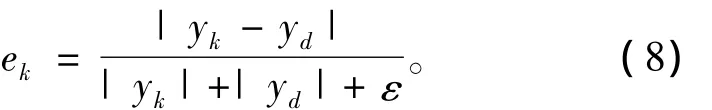
式中:k表示CMAC网络的迭代步数;ε为任意小的正数。

通过ek得到相应的动态学习率。表示为ηk= ek。相应的权值更新函数见式(9)。

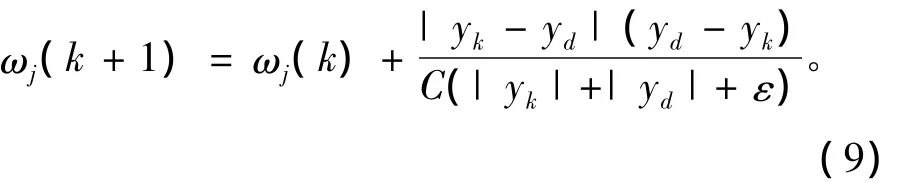
修改后的CMAC网络模型的学习率是由每个迭代步的误差决定的。因此此模型采用的学习率适应网络中的每一步学习。

2 仿真实验

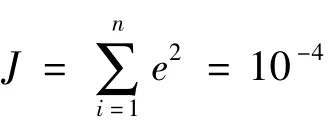
本文采用8个标准模式和69个非标准模式作为模型的输入。表1中给出了分别利用传统CMAC识别模型和本文提出的识别模型进行实验后得出的结果中的9个仿真结果。

如表1所示，含有动态学习率的CMAC识别模型的识别精度比传统的识别网络模型明显要高。

表2给出了3种不同的板形识别模型的比较结果。此仿真实验中，50个模式被用做训练样本，25个模式被用做测试样本。利用传统的CMAC识别模型方法得到的MSE为0.092 9，采用本文提出的新模型MSE仅为0.070 0。

如表2所示，利用这50个样本训练时，方法1的训练时间最长，其训练时间大约是方法2的10倍。方法3的训练时间是最短的，仅有10 s。因此，板形模式识别的精度和速度都大大得到了改进。

3 结论

本研究建立了一种新的具有动态学习率的CMAC神经网络板形识别模型，具有如下3个特点。

1)基于勒让德正交多项式的基模式符合实际的板形模式识别的要求。

2)采用了欧式距离差作为模型的输入，物理意义明确，简化了网络结构，进一步实现了网络结构的固定化和简单化。此改进的板形模式识别方法可推广到其他模式识别系统中，特别是基本模式具有两两互反性的模式识别系统中。

3)误差校正算法中引入了动态学习率。同具有固定学习率的传统方法相比较，这种方法节省了训练时间，同时识别精度也得到了提高。

表1 3种识别模型的识别结果Tab.1 Contrast of experimental results by three recognition model

表2 3种不同板形模式识别模型的比较Tab.2 Comparison among three different models for flatness pattern recognition

/References:

［1］ 彭 艳，刘宏民.冷轧带钢板形检测信号模式识别方法的进展［J］.燕山大学学报，2003，27(2):142-145.

PENG Yan，LIU Hongmin.Pattern recognition method progress of measured signals of shape in cold rolling［J］.Journal of Yanshan University，2003，27(2):142-145.

［2］ 张秀玲，刘宏民.变结构神经网络在板形信号模式识别方面的应用［J］.钢铁研究学报，2001，13(2):88-92.

ZHANG Xiuling，LIU Hongmin.Pattern recognition of shape signal by variable structure neural network［J］.Journal of Iron and Steel Research，2001，13(2):88-92.

［3］ ALEKSANDER K.Basic function model of the CMAC network［J］.Neural Network，2000，12(5):107-126.

［4］ ALBUS J S.A new approach to manipulator control:The cerebellar model articulation controller(CMAC)［J］.Journal of Dynamic System Measurement and Control，1975，97:220-227.

［5］ MILLER W T，GLANZ F H，KRAFT L G.CMAC:An associative neural network alternative to backpropagation［J］.Proceedings of the IEEE，1990，78(9):1561-1567.

［6］ 张秀玲，刘宏民.板形模式识别的GA-BP模型和改进的最小二乘法［J］.钢铁，2003，38(10):29-34.

ZHANG Xiuling，LIU Hongmin.GA-BP model of flatness pattern recognition and improved least squares method［J］.Iron and Steel，2003，38(10):29-34.

［7］ JIA Chunyu，SHAN Xiuying，LIU Hongmin.Fuzzy neural model for flatness pattern recognition［J］.Journal of Iron and Steel Research International，2008，15(6):33-38.

［8］ PENG Y，LIU H M.A neural network recognition method of shape pattern［J］.Journal of Iron and Steel Research International，2001，8(1):16-20.

［9］ WONG Y，SIDERIS A.Learning convergence in the cerebellar model articuation controller［J］.IEEE Trans Neural Networks，1992，3(6):115-121.

［10］ 张 材，谭建平.基于遗传算法反向传播模型的板形模式识别［J］.中南大学学报(自然科学版)，2006，37(2):294-299.

ZHANG Cai，TAN Jianping.Strip flatness pattern recognition based on genetic algorithms-back propagation model［J］.Journal of Central South University(Science and Technology)，2006，37 (2):294-299.

［11］ WANG J.A flatness pattern recognition model based on wavelet transform and probabilistic neural network［J］.Information Computing and Applications Communications in Computer and Information Science，2012，308:187-194.

［12］ 张雪伟，王 焱.智能识别方法在板形识别中的应用及发展趋势［J］.钢铁研究学报，2010，22(1):1-3.

ZHANG Xuewei，WANG Yan.Application and development trend of intelligent recognition methods for flatness recognition［J］.Journal of Iron and Steel Research，2010，22(1):1-3.

［13］ 单修迎，刘宏民，贾春玉.含有三次板形的新型板形模式识别方法［J］.钢铁，2010，45(8):56-58.

SHAN Xiuying，LIU Hongmin，JIA Chunyu.Analysis of a new flatness pattern recognition method containing the cubic flatness［J］.Iron and Steel，2010，45(8):56-58.

［14］ 张秀玲，赵文保，张少宇.基于改进T-S云推理网络的板形模式识别方法［J］.中南大学学报(自然科学版)，2013，44 (2):580-586.

ZHANG Xiuling，ZHAO Wenbao，ZHANG Shaoyu.Method of flatness pattern recognition based on improved T-S cloud inference network［J］.Journal of Central South University(Science and Technology)，2013，44(2):580-586.