面向广域阻尼控制的电力系统降阶辨识研究

， ， ，

(1.国网四川省电力公司，四川 成都 610041；2.国家电网公司，北京 100031)

0 引 言

大区电网互联的形势下，低频振荡问题已成为限制省间和区间功率传输极限的瓶颈，即使安装了大量传统的励磁附加阻尼控制器(power stability stabilizer，PSS)，区间低频振荡问题仍然没有得到有效解决[1]。广域测量技术的发展和普及使得采用广域信号作为阻尼控制的输入信号成为可能，研究表明[1]，对于抑制区间低频振荡，广域阻尼控制与本地阻尼控制相比具有明显优势。

在广域阻尼控制中，传统PSS设计中所采用的单机无穷大系统的假设已经不再适用。学者们陆续提出了基于极点配置、最优控制及鲁棒控制等现代控制理论的广域阻尼控制器设计方法，然而这些方法都要基于系统模型，因此系统模型的获取是设计广域阻尼控制器的关键。降阶辨识方法为获取电力系统控制器设计可用的模型提供了一种有效手段。

系统辨识的方法众多，基于模型的方法主要有预报误差法(prediction error method, PEM)和子空间辨识法两种，对于系统辨识的算法实现、辨识的收敛性和一致性、辨识误差的分布、模型的定阶方法以及辨识实验的最优激励信号和最优预滤波器设计方法，L. Ljung在其经典巨著[2]中做了系统的总结。相比之下电力系统中面向控制的辨识研究开展的较少，I. Kamwa在这方面做了很多先驱性的工作，他采用子空间辨识等方法为电力系统MIMO控制器设计提供模型，获得了很好的仿真效果[3]。文献[4]采用PEM辨识方法获得了系统模型，并在此基础上进行了MIMO最优控制器设计。系统辨识方法在电力系统中应用的同时，在降阶原理及方法体系方面还有待研究，包括：① 电力系统面向阻尼控制器设计的可降阶原理：电力系统的阶数有成千上万阶，可以用几阶到十几阶的模型来表示的原因；降阶的误差分析；降阶模型阶数的确定等等； ② 电力系统的降阶辨识方法体系：电力系统辨识可用的方法；面向广域阻尼控制误差度量；辨识实验的激励信号、预滤波器设计等等。

1 电力系统的可降阶原理与降阶误差分析

1.1 模式可控可观性与系统降阶

电力系统线性模型可以表示成解耦状态方程[6]为

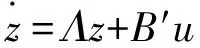
(1)

y=C′z

(2)

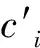
此时系统可表示成

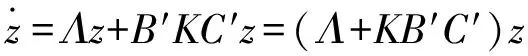
(3)

(4)

经过矩阵行变换，式(4)与式(5)的特征值相同为

(5)

其中，P为行变换矩阵。注意到，式(5)所示矩阵即式(6)所示系统的闭环状态矩阵。

(6)

式(6)所示系统由不受控和受控两解耦的子系统构成，其中受控的子系统不含有与不可控模式相关的状态变量，因此其阶数是原系统的阶数减去不可控的模式数。控制器设计可针对该受控子系统进行，与在原系统上设计控制器是等同的。

由上述分析可知，当系统存在不可控的模式时，对于控制器设计而言，可以对系统进行降阶，降阶后的系统不含有不可控的模式。由对偶原理可知，当存在不可观的模式时，系统同样也可以被降阶。上述证明是在控制器为比例环节的假设下完成的，对于一般情况，通过将控制器表述成状态方程形式与系统的解耦状态方程联立，通过类似的证明过程可以得到相同的结论，此处从略。

当存在不可控或不可观的模式时，对于控制器设计而言，被控系统可以被降阶而不损失有用的信息。由此可以推想，当存在可控可观性相对很弱的模式时，在承受一定的误差的前提下，也可以对被控系统进行降阶。后一种情形在电力系统中更为常见。对于阻尼控制器设计而言，以PSS设计为例，虽然电力系统阶数很高，但是单台发电机参与的模式有限，且本地反馈信号也只对本地模式和部分区间模式可观性较强，因此对于PSS的设计而言，其对于系统的大部分模式是不可控不可观或者极弱可控、可观的，因此可以对系统进行大规模的降阶。

引入广域信号作反馈后，由于信号的选择不受限制，可以挑选对区间模式具有强可观性的信号，且由于控制点和反馈信号的选择可以分离，对控制点可控的本地模式，可以选择反馈信号使之不可观，使得控制器既可控又可观的模式集中在区间振荡模式，从而可以进一步降低系统的阶数。

1.2 降阶模型的误差

考虑单输入单输出系统G(s)。G(s)的传递函数可写成如下形式(假设特征方程无重根)。

(7)

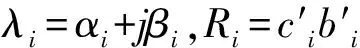
(8)

当Rr+1=Rr+2=…=Rn=0，自然有Gr(s)=G(s)。

如果Rr+1≠0，降阶会带来误差。该误差为

(9)

该误差是被舍去的模式所引入的误差之和。模型误差可以用H∞范数和H2范数来评估。

用H∞范数来评估模型误差，可以考察模型误差的幅频响应的峰值。模式λi在G(s)中对应的项为Ri/(s-λi)，该项在频域上的最大幅值为|Ri|/|αi|，舍去该模式所带来误差的H∞范数即为|Ri|/|αi|。由于各模式对应幅频上的峰值不出现在同一频率，因此式(9)所示误差范数的上限和近似的下限为

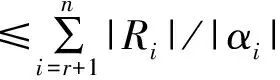
(10)

该上限保守性太强，下限更接近误差的真实值。用H2范数来评估模型误差，可以反映在整个频谱范围内误差的总体大小，同时也对应模型与实际系统间单位冲激响应之差的能量。

模式λi对应项Ri/(s-λi)的H2范数平方为[5]

(11)

由于单位冲激脉冲响应的总能量近似等于各模式能量的和，式(9)所示误差的H2范数可近似由式(12)表示。

(12)

无论是范数还是范数下的误差表示都反映出，舍去留数小且阻尼大的模式所带来的模型误差较小。误差的大小是相对的，误差范数相对于系统范数的相对大小更能准确地评价模型的质量。

1.3 基于降阶原理和BIC准则的模型定阶方法

模型定阶是辨识过程中非常重要的一环。令辨识的相对误差小于ε0，由降阶原理做出的模型阶数估计由式(13)给出。

‖ΔGr(s)‖≤ε0‖G(s)‖≤‖ΔGr+1(s)‖

(13)

其中，‖·‖可以是H∞范数或H2范数，‖ΔGr(s)‖的计算公式由式(9)、(10)和(11)给出，随着阶数的增加单调递减。‖G(s)‖为系统的总范数。

采用降阶理论给出了阶数的估计后，在辨识过程中再采用传统的定阶准则来做调整和校核。传统的BIC定阶准则[87]为

BIC(p)=NlnVN+plnN

(14)

其中，p为模型阶数；N为采样点数；VN为预报误差的方差。该准则包含了对拟合精度的评价和对模型阶数的惩罚两部分。降阶原理与BIC准则的结合，赋予了定阶方法清晰的物理意义，改变了传统BIC等方法依赖辨识拟合程度大量试算的局面。

2 电力系统的降阶辨识实验设计

降阶的可行性是用低阶模型来辨识系统的基础。系统辨识常用方法主要有预报误差法和子空间辨识法两大类[2]，其中预报误差法使用最为广泛，并可用于闭环辨识。这里以预报误差法为例讨论辨识实验中的激励信号和预滤波器设计。

待辨识的系统如下表示。

y(t)=G0(q)u(t)+H0(q)e(t)

(15)

其中，q是移位算子；G0是被控系统；u是激励信号输入；y是测量输出；e是方差为λ0的白噪声；H0是噪声模型。辨识模型与实际系统间总会存在误差，其大小可以用模型与实际系统之差的方差和偏差来评价，定义模型品质度量的准则函数[2]为

(16)

其中，G(ejω,θ)为辨识模型的频域表示；C(ω)为品质加权函数，对应在不同频率段对辨识精度的不同要求。J(θ)近似可分解为“方差贡献”JV(θ)与“偏差贡献”JB(θ)之和。对于开环辨识情况，JV(θ)可表示为[2]

(17)

其中，n是模型阶数；N是采样数据点数；Φv(ω)为辨识中噪声的功率谱，有Φv(ω)=λ0|H0(ejω)|2Φu(ω)为激励信号的功率谱。

为使得JV(θ)最小，最优激励信号设计[2]为

(18)

其中，μ是可调常数。为使得偏差贡献项JB(θ)最小，应满足式(19)[2]。

Φu(ω)|L(ejω)|2/|H(ejω,θ*)|2=kC(ω)

(19)

其中，H(ejω,θ*)为N趋于无穷时噪声模型的收敛值；k是可调常数。

对于以广域阻尼控制器设计为目的的电力系统降阶辨识，推导相应的品质加权函数C(ω)如下。

广域阻尼控制器的参考信号一般为零，系统的输入和输出满足如下方程。

u(t)=-K(q)y(t)

y(t)=G0(q)u(t)+v

(20)

其中，K为反馈控制器；v代表外部扰动。系统只受外部扰动激励；y=S0v,S0为输出灵敏度函数，S0=1/(1+G0K)。令R(q)为

R(q)=G(q,θ)/〔1+G(q,θ)K(q)〕

(21)

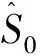
(22)

为使得设计系统输出逼近实际系统输出，必须极小化目标函数为

J(G)=

(23)

对比式(16)，可知此时的C(ω)为

(24)

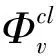
(25)

(26)

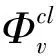
以上激励信号和预滤波器的设计方法在实际应用中显得非常复杂，式(18)和(26)给出了一个结论：在辨识精度要求高的频率段，激励信号谱和预滤波器幅频响应都应该具有更大值。由于辨识出的模型会用于设计控制器以阻尼低频振荡，C(ω)在低频段会有更大的值，一种实用的简化设计方法是把激励信号谱和预滤波器设计成低通的形式，将截止频率设置在一般振荡的最高频率2 Hz左右。

设计出激励信号的谱后，滤波后的高斯白噪声是一种频域和时域特性都较为理想的激励信号实现方式，此外还需要结合对激励信号的幅值和能量的限制来确定可调系数μ[2]。

3 仿真算例分析

仿真算例在四机两区系统上进行，仿真工具为Matlab，系统如图1所示，各元件参数与文献[6]相同。

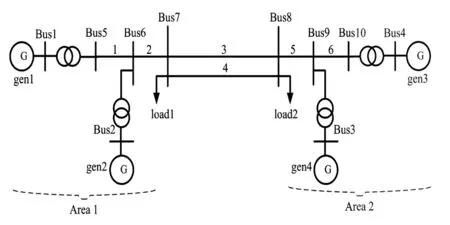
图1 四机两区系统示意图

每台发电机都配备励磁和调速系统，系统共54阶。以发电机4的励磁参考电压为控制点，分别以机端功率和区域1与区域2间的交换功率作为反馈信号，考查面向本地控制和广域控制的电力系统可降阶情况。分析的结果见表1，为简化篇幅，省略了大量无关紧要的左半平面实轴上的非振荡模式。

由表1可知，系统有3个弱阻尼的机电振荡模式，其中0.557 7 Hz模式为区间振荡模式，1.104 9 Hz模式为G3/G4间的本地振荡模式，1.131 6 Hz模式为G1/G2间的本地振荡模式；其他模式为阻尼情况很好的控制器及磁链模式。G4对于G3/G4本地模式及区间模式的可控性较强，对于G1/G2的本地振荡模式可控性很差，且对于大量与G4不相关的控制器/磁链模式不具有很强的可控性；同样G4机端功率信号对于G1/G2模式的可观性很差，且对于大部分控制器/磁链模式基本不具有可观性；相比本地信号，广域的区域交换功率信号的模式可观性基本集中在区间振荡模式，对于其他本地模式及控制器/磁链模式的都基本不可观。

结合前述基于模式可控可观性的可降阶原理可知，此系统可以实现大规模的降阶来简化控制器的设计。以模型误差10%为限，用H2范数来评估误差，本地控制需要保留的模型阶数为8阶，广域控制为3阶；用范数评估误差，本地控制需要保留的模型阶数为10阶，广域控制为4阶。该分析结果表明，降阶的程度与控制点和反馈信号的选择相关，而对电力系统的大规模降阶是可行的。

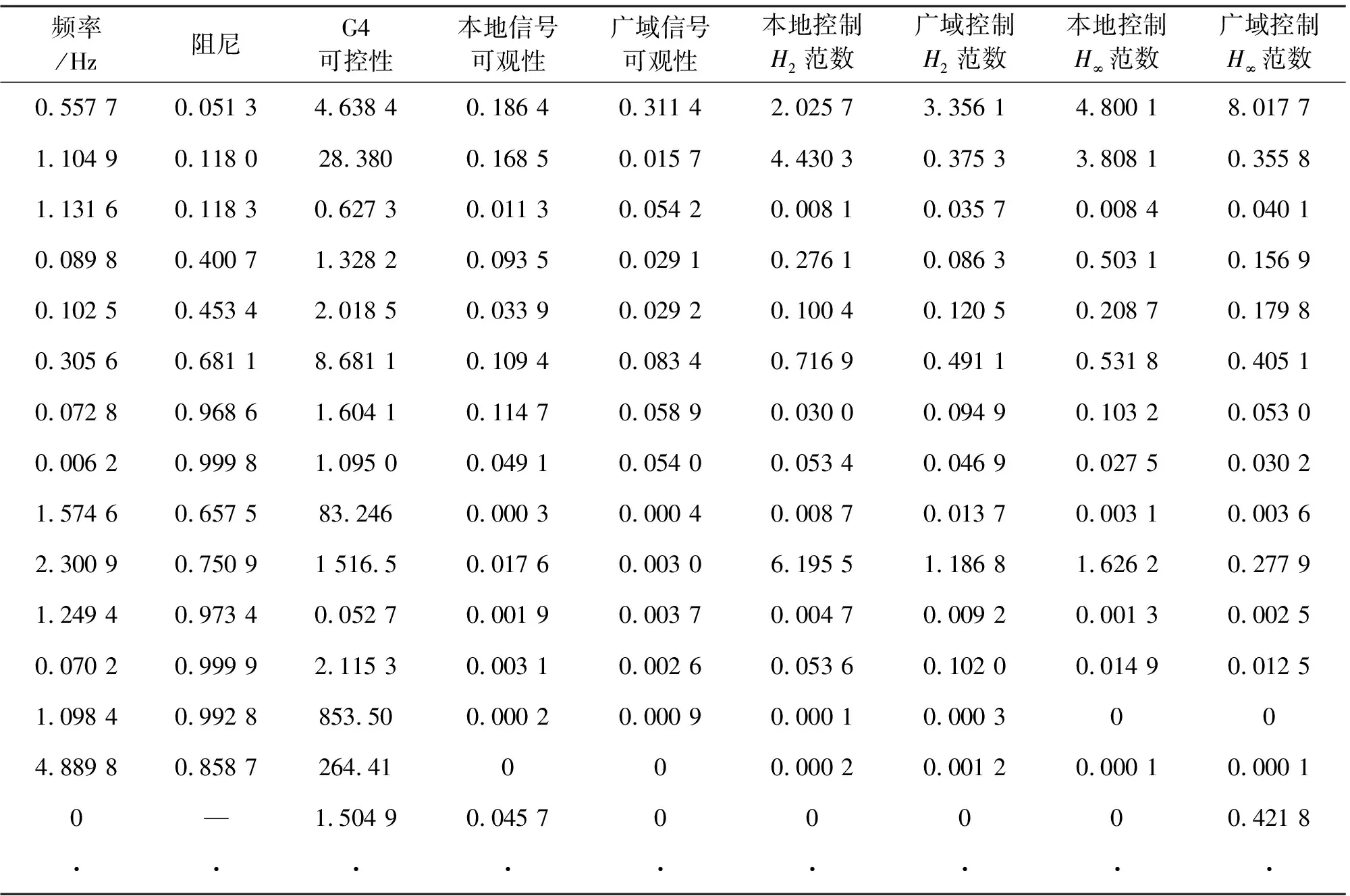
表1 四机两区系统模式可控可观性分析

采用PEM的方法辨识从控制点到广域反馈信号的被控系统模型，采样率为10 Hz，仿真时长为40 s。由于实际系统模型未知，因此首先将激励信号谱和预滤波器设计成低通的形式，截止频率为2 Hz，激励信号选用滤波后的高斯白噪声，滤波器为二阶巴特沃兹低通滤波器，衰减率取为0.707。辨识得到的各阶模型拟合度如表2所示。

由上述基于降阶原理的估计可知，采用3阶模型已能较好地拟合系统。从表2可以看出，随着模型阶数从3阶上升到11阶，模型的拟合精度并没有显著提高，这反映了降阶理论对模型阶数做出的估计是合理的。辨识出的3阶模型含有一对频率为0.58 Hz、阻尼比为5.47%的极点，与表1的小干扰分析结果基本相同。根据BIC准则进行最后的校验，确定模型的阶数为3阶。

表2 不同模型阶数下的拟合度

根据辨识的3阶模型采用极点配置的方法[6]设计出广域阻尼控制器，与本地PSS控制相比较，控制效果如图2所示，其中PSS参数由文献[6]给定。可见，与本地PSS控制相比，广域阻尼控制对于区间低频振荡的阻尼更强，该算例同时也表明广域阻尼控制器的设计可以基于降阶辨识模型进行。

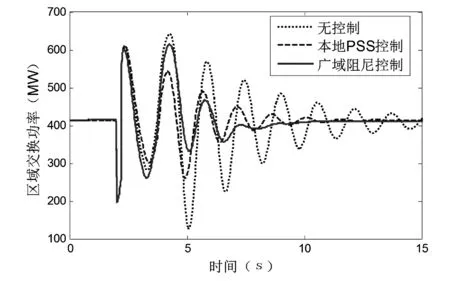
图2 根据辨识模型设计广域阻尼控制器的控制效果

根据辨识出的系统模型和噪声模型，以及所设计的控制器，按照式(25)和式(26)重新设计得到如图3所示最优输入信号谱和最优预滤波器幅频特性。

两者都具有明显的低通特性，在主导振荡频率0.58 Hz及以下频率有较大值，截止频率在0.8 Hz左右，比本辨识实验中采用的截止频率2 Hz略低。可见，由于电力系统呈低通特性，且低频振荡频率小于2 Hz，因此将输入信号谱和预滤波器设计为低通特性，截止频率取为高于低频振荡频率，是一种适用性较强的设计方案。

4 结 论

电力系统降阶的可行性是能够用低阶模型来辨识系统的基础。基于模式可控可观性分析，提出了面向广域阻尼控制器设计的电力系统可降阶原理，并提出了H∞/H2范数下的降阶误差分析方法，以及降阶原理估计和BIC准则结合的模型定阶方法。进一步地，针对广域阻尼控制器设计，提出了辨识实验中的最优激励信号和最优预滤波器设计方法，并指出采用具有低通特性的激励信号谱和预滤波器是一种实用的设计方案。四机两区系统上进行的仿真表明了上述方法和理论的有效性。

[1] 谢小荣, 肖晋宇, 童陆园,等. 采用广域测量信号的互联电网区间阻尼控制[J]. 电力系统自动化, 2004, 28(2):37-40.

[2] Lennart Ljung. System Identification——Theory for the User(2nd ed)[M]. USA: Prentice Hall, 2002.

[3] Kamwa I, Luc Gerin-Lajoie. State-space System Identification-toward MIMO Models for Modal Analysis and Optimization of Bulk Power Systems[J] . IEEE Trans. on Power Systems, 2000, 15(1):326-335.

[4] Lu Chao, Li Licheng, He Jingbo, et al. Optimal Coordinate Design of Multiple HVDC Modulation Controllers based on MIMO System Identification [C]. 2007 IEEE PES General Meeting, 2007:1-8.

[5] Xie Xiaorong, Lu Chao. Optimization and Coordination of Wide-area Damping Controls for Enhancing the Transfer Capability of Interconnected Power Systems[J]. Electric Power Systems Research, 2008, 78:1099-1108.

[6] Kundur P. Power System Stability and Control [M]. New York: McGraw-Hill, 2001.