西北太平洋跨等密度面湍流混合的时空变化分析*

闫晓梅 李 颖, 徐永生①

(1. 中国科学院海洋研究所 青岛 266071; 2. 中国科学院海洋环流与波动重点实验室 青岛 266071;3. 中国科学院大学 北京 100049)

海洋中的跨等密度面湍流混合对于热量输运、水体交换以及全球气候、热盐环流强度都有重要影响,因此研究混合的时空变化特征及其影响因素具有重要意义。早在20世纪60年代, Munk等(1966)就指出,为了维持深海的层结结构, 至少需要大洋平均扩散系数为10–4m2/s。但是随后的观测实验发现远离边界的大洋内区的扩散系数仅为10–5m2/s(Gregg, 1987;Ledwellet al, 1993)。直至上世纪90年代之后, 在海底地形粗糙的海山(Luecket al, 1997)、海脊(Polzinet al, 1997)、峡谷(Carteret al, 2002)等处观测得到了强扩散系数, 可达O(10–4m2/s)甚至更强。

海洋内部混合主要由内波破碎导致, 而除了正压潮流与粗糙地形相互作用激发的内潮外, 海表面风应力是内波场的另一个重要能量来源, 因此风输入到海洋中的能量随时间的变化将导致混合的变化。已有研究发现上层海洋混合存在明显的季节变化,而且与海表面风应力密切相关(Jinget al, 2010, 2011;Wuet al, 2011)。但在不同海区, 风应力的影响深度有所差异, 如在西太平洋137°E断面上为300—1500m(Jinget al, 2010), 在副热带西北太平洋的吕宋海峡及黑潮源地为300—600m(Jinget al, 2011), 在夏威夷岛附近为300—600m(荆钊, 2012), 在南极绕极流区域是1000—2000m(Watermanet al, 2013)。

由于西北太平洋海区地形复杂, 而且有大量的风生近惯性能量输入(Alford, 2001), 因此海洋混合必将具备一定的空间分布特征, 同时, 上层的湍流混合也将随风应力存在一定的季节变化。为此, 本文利用历史水文观测剖面资料, 基于细尺度参数化方法研究该区域的跨等密度面湍流混合的时空特征, 以及风应力对上层海洋混合的影响深度。

1 数据和方法

1.1 数据

本文采用日本海洋数据中心(JODC)提供的高分辨率CTD剖面资料, 选用空间区域135°—180°E、25°—45°N, 且采用资料较多的时间段2000—2007年。经过质量控制后, 只取采样深度超过600m的剖面, 得到共计8609个站位, 站位分布如图1。由于剖面数据的垂向分辨率小于2m, 因此统一将温度、盐度垂直插值到2m间隔以便于湍流混合的计算分析。同时, 采用了美国国家地球物理数据中心(NGDC)2006年发布的全球海底地形数据ETOPO2v2来计算地形粗糙度, 该数据空间分辨率为2′×2′, 本文取1/3°×1/3°网格区域内的地形高度的方差(Kunzeet al,2006)。定义平坦地形为粗糙度小于1.0×105m2, 而粗糙地形则为粗糙度大于1.0×105m2。这一临界值的选取参考了研究区域总体地形粗糙度以及各站位所在位置的平均地形粗糙度(图3—4), 而且临界值的微小变动不影响本文的分析结果。

此外, 为了计算风生近惯性能量, 采用了海表面风应力和混合层深度数据。其中, 风应力数据来自美国国家环境预报中心和国家大气研究中心再分析资料(NCAR/NCEP), 时间分辨率是6小时, 而混合层深度数据采用的是来自Levitus 94数据集的气候态月平均资料。

图1 西北太平洋的海底地形, 黑点表示历史水文观测站位, 将研究区域划分为6个子区域Fig.1 Bathymetry of the northwestern Pacific. Black dots are historical hydrographic stations. The study region is divided into six sub-regions marked in Roman numbers

1.2 细尺度参数化方法

海洋内部的扩散系数与耗散率是研究混合的两个有效参量。内波间的相互作用不断地将能量从大尺度向小尺度传播, 内波破碎引发湍流混合, 基于这一思想, 可将细尺度上的由内波引起的垂向剪切及应变与扩散系数及耗散率联系起来(Gregget al, 2003;Kunzeet al, 2006), 因此扩散系数被参数化为:

其中K0=0.5×10–5m2/s,代表观测到的应变方差,是GM应变谱的方差(Gregget al, 1991),f是科氏参数,N是浮力频率。在公式(1)中,

f30=f(30°),N0=5.2×10–3rad/s,Rω代表剪切应变方差比,参考Kunze等(2006), 本文中设为常数7。由于缺乏流速剖面观测, 难以直接估算Rω。Kunze等(2006)利用印度洋、太平洋、北大西洋和南大洋中的3500个LADCP/CTD剖面资料, 计算得到Rω=7±3。本文采用固定值7, 通过代入方程(2)导致的不确定度约为2倍。同时, 由于细尺度参数化方法估算的扩散系数的不确定度在2倍之内(Polzinet al, 1995)。所以, 本文计算结果的不确定度应该是在4倍之内。

为了计算扩散系数和耗散率, 将每个站位的剖面资料划分为一系列320m的子剖面, 并取160m重叠。由浮力频率计算得到应变其中(σ代表位势密度), 而是通过对子剖面内的位势密度进行线性拟合得到。然后利用傅里叶变换得到zξ的应变谱φ(k), 其中,k是垂直波数。为计算应变方差比首先选取最小波数kmin=2π/150m(即对应最大波长为150m), 以这一最小波数为积分下限计算应变方差(Kunzeet al,2006), 使其满足

从而得到最大波数kmax, 然后在同样的区间[kmin,kmax]计算GM应变方差

其中, 无量纲能量E0=6.3×10–5, 温跃层的垂向尺度b=1300m, 参考模态j*=3, 参考波数(b·N0),N0=5.2×10–3rad/s(Gregget al, 1991)。得到扩散系数后, 耗散率即可根据关系式得到, 其中混合效率Γ=0.2(Osborn, 1980)。

在表层300m以浅, 混合层与季节性温跃层的影响将导致用细尺度参数化方法计算的扩散系数与耗散率有很大的误差, 因此本文只采用300m以深的剖面数据来研究混合的时空变化特征。另外, 通过Lilliefors检验(Lilliefors, 1967), 发现相比于正态分布,所有剖面的扩散系数κ和耗散率ε更倾向于对数正态分布(图2), 因此本文中所涉及到的κ和ε平均, 均采用几何平均。同时, 从深度D1到D2垂直平均的耗散率是指

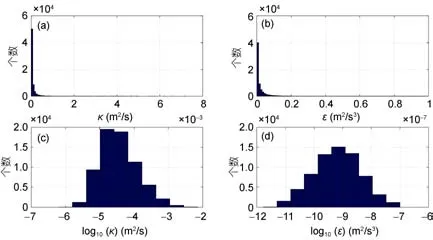
图2 (a)扩散系数κ(单位: m2/s)与(b)耗散率ε(单位: m2/s3)的分布, 以及取对数后的(c)扩散系数log10(κ)(单位: m2/s)与(d)耗散率log10(ε)(单位: m2/s3)的分布。Fig.2 Distributions of (a) diffusivity κ (unit: m2/s) and (b) dissipation rate ε (unit: m2/s3), and that of the logarithm of (c) diffusivity κ(unit: m2/s) and (d) dissipation rate ε (unit: m2/s3)

1.3 风生近惯性能量的计算

风生近惯性能量是上层海洋中内波场的重要能量来源。风输入到混合层中的近惯性能量可以通过海表面风应力与混合层流速直接计算得到, 但是由于混合层速度不易获得, 本文采取Pollard等(1970)提出的一个slab模型, 直接利用风应力资料和混合层深度来计算风生近惯性能量。

对于混合层内流速分量u和v, D’Asaro(1985)得到其控制方程为:

其中Z=u+i ·v代表混合层流速,f是科氏参数,H是混合层深度,T=(τx+i·τy)/ρ是风应力,ρ为海水密度,r是依赖于频率的衰减系数(Alford, 2003)。

其中σ代表角频率,r0=0.15f,σc=f/2。

本文先将时间分辨率为6小时的风应力数据插值到8分钟的时间格点上, 再将控制方程进行傅立叶变换, 从而得到频域的解为:

由于当惯性频率f接近或超过NCEP风场的Nyquist频率(2cpd)时, 由以上方法计算的能量通量将偏小, 因此本文在纬度高于40°的区域进行了修正。参考Alford(2003), 取修正系数α在40°N处为1, 在70°N处为0.5, 将其在40°—70°N之间进行线性插值, 得到修正的能量通量为Π/α。最后, 将计算的能量通量进行日平均后再进行分析。

2 结果与分析

2.1 空间分布

西北太平洋的地形较为复杂, 日本以南140°E处有伊豆-小笠原海脊, 水深仅1000m, 而日本群岛以东是一狭长的水深超过8000m的日本海沟, 其东侧则是地形较为平坦的大洋内区, 水深约6000m, 只有165°E和170°E附近水深较浅约3000m(图1)。西北太平洋地区的地形起伏变化明显, 同时, 跨等密度面的混合也呈现显著的空间变异。计算观测站位所处位置的地形粗糙度及300m以深垂直平均的耗散率, 结果如图3所示。可以看到, 耗散率在日本近岸的海沟附近较大, 尤其是在日本以南的伊豆–小笠原海脊处最大, 而在日本以东的大洋内区较小(图3b), 这一空间分布与地形粗糙度的空间分布(图3a)相似。在地形粗糙的区域, 耗散率达到O(10–8m2/s3), 而在地形平坦的区域, 耗散率仅O(10–11m2/s3)。该结果与Whalenet al(2012)利用全球ARGO资料计算的结果一致(参考其图1)。

图3 (a)地形粗糙度log10(roughness)(单位: m2)与(b)300m以深垂直平均的耗散率log10(ε)(单位: m2/s3)的空间分布Fig.3 Spatial distribution of (a) bottom roughness log10(roughness) in m2 and (b) vertically averaged below 300m dissipation rate log10(ε) in m2/s3

进一步地, 计算了该区域经向平均的背景浮力频率、耗散率及地形粗糙度, 如图4所示。伴随着背景层结随深度增加而减弱, 耗散率也明显地随深度增加而衰减, 上层达O(10–8m2/s3), 而深层仅O(10–11m2/s3)。耗散率的这一垂直分布与Kunze等(2006)利用太平洋海区CTD数据计算的结果一致。另外, 在上层海洋, 背景浮力频率随经度先减小, 至145°E附近后再增大; 而在1500m以深, 尤其是在1500—4000m, 浮力频率随经度的变化不再明显。相反地, 耗散率与背景层结的这一空间变化明显不同(图4b)。在142°E附近的伊豆-小笠原海脊处, 地形变化最为剧烈, 粗糙度超过106m2, 相应的耗散率超过10–8m2/s3。而在173°E, 30°N附近, 地形也较为粗糙,起伏方差达6×105m2, 相应的耗散率接近10–9m2/s3。垂直平均的耗散率随经度自西向东存在一个减弱的趋势(图4c)。总体上, 垂直平均的耗散率与地形粗糙度的变化有很好的一致性, 两者之间的相关系数达0.71, 超过95%显著性检验。例外的地方是在137°E附近, 地形虽然较为平坦, 但耗散率很强, 可达到10–8m2/s3。Qiu等(2012)在分析西北太平洋中的137°E断面上的跨等密度面湍流混合时, 同样发现在25°—29°N区间地形较为平坦而混合较强, 并指出这是由次谐波不稳定性导致。而对于耗散率的经向差异,主要是由于西部的伊豆–小笠原海脊是西北太平洋的一个重要的半日潮生成区, 而内潮与地形相互作用将引起强混合(Niwaet al, 2001; Simmonset al,2004)。根据St. Laurent等(2002), 内潮能量可以辐射的空间尺度达O(1000km), 因此在伊豆-小笠原海脊东西两侧约5°范围内的混合依然很强。另外, 从图4b也可看出, 地形对混合的影响可至海底之上2000—3000m, 尤其是在伊豆-小笠原海脊附近。Kunze等(2006)在全球若干海区包括日本以南都发现近海底的强混合可向上延伸至主温跃层, 而这些海区都具有粗糙的地形及较强的近海底流。考虑到黑潮延伸体强流流经此处, 因此这里由海底至上层的强混合除了由内潮维持之外, 很可能与黑潮延伸体与粗糙地形相互作用有关。

图4 经向平均的(a)背景层结log10(N2) (单位: 1/s2)与(b)耗散率log10(ε) (单位: m2/s3)的经度-深度分布及(c)垂直平均的耗散率(蓝线)与地形粗糙度(黑线)随经度的分布Fig.4 Spatial distribution of the meridional-mean (a) background stratification log10(N2) in 1/s2 and (b) dissipation rate log10(ε) in m2/s3,and (c) vertically averaged meridional-mean dissipation rate (from 300m to bottom) against longitude (blue solid) as well as the bottom roughness (black solid)

2.2 风强迫的上层海洋混合及其季节变化

除了内潮与地形的相互作用, 风生近惯性能量也对维持海洋内部的混合有重要意义。风应力使得在海表面混合层内产生近惯性流, 一部分能量在表层耗散掉, 另一部分能量以近惯性内波的形式向下传播从而影响海洋深层的湍流混合(Nagasawaet al,2000; Zhaiet al, 2009)。已有研究表明, 风应力对于海洋混合的季节变化有明显作用, 但在不同海区存在不同的影响深度 (Jinget al, 2010; 荆钊, 2012;Watermanet al, 2013)。为此, 本节将研究风应力影响深度在西北太平洋海区的空间分布。

为研究风应力对湍流混合的影响, 首先应尽量去除地形的影响, 因此根据上一节的分析结果, 本文选取地形平坦的区域且距离海底4000m的剖面数据,最终得到2833个剖面资料。首先从能量平衡的角度看, 在西北太平洋区域, 平均风生近惯性能量为1.8×10–3W/m2, 而在平坦地形处, 300—600m与300—1800m垂直积分的耗散率分别为7.6×10–4W/m2,1.8×10–3W/m2, 与风输入该海区的能量相当。这一结果意味着在西北太平洋海区, 风输入能量对于维持上层海洋混合具有重要作用, 但是风对混合的影响深度仍不清楚。为此, 本文将研究区域划分为6个子区域(图1), 每个子区域的观测剖面个数分别为359、206、201、441、1054、572, 可以保证每个子区域都有足够的剖面资料用来研究混合随时间的变化及风应力的影响深度。

在每个子区域, 对每一深度的耗散率, 先计算其区域平均, 再计算其季节平均(本文取春季为3—5月,夏季为6—8月, 秋季为9—10月, 冬季为12—2月,因此2000—2007年共得到32个数据)。同样地, 计算相应区域平均的风生近惯性能量的季节变化, 然后分析两者的相关性, 得到每个区域耗散率与风生近惯性能量相关系数的垂直分布, 结果如图5所示。可以看到, 除了子区域VI外, 其余5个子区域的相关系数在上层都比较显著, 直到到达某一深度后, 相关性不再明显, 将这一深度定义为风应力的影响深度。得到在五个子区域I—V中, 风应力对上层海洋中混合的影响深度分别为620m, 940m, 940m, 1740m,1420m。其中, 日本以南伊豆-小笠原海脊以西的子区域I的影响深度最浅仅620m, 而日本东南的子区域IV的影响深度最深达1740m, 沿着日本海沟的子区域II和III的影响深度均为940m, 日本海沟以东的子区域V的影响深度也较深为1420m。对于子区域VI,海洋上层的耗散率与风生近惯性能量的相关关系较弱, 而在940m处存在一显著相关, 意味着在大洋内区, 上层海洋混合的季节变化除了受风应力影响之外还受其它因素的调制。

图5 对应图1中6个子区域的耗散率与风生近惯性能量相关系数随深度的变化红色虚线为95%显著性检验。Fig.5 The correlation coefficients between dissipation rate and wind-induced near-inertial energy at different depths. Red dashed lines represent 95% significant level

对每个子区域中风应力影响深度以内的耗散率取垂直平均(对子区域VI, 取940m以浅), 再将其与风生近惯性能量进行线性拟合, 结果如图6所示。同样可以看到, 除了大洋内区的子区域VI外, 季节平均的耗散率与风生近惯性能量存在很好的一致性,相关系数最小0.57, 最大0.75, 均超过95%显著性检验。同时, 线性拟合系数存在一定的空间差异, 在风应力影响深度最大的子区域IV, 拟合系数最小为0.10, 意味着风应力对上层海洋混合季节变化的影响程度较小, 而在日本近岸的子区域I—III, 拟合系数最大达0.17, 说明该地区的风应力对混合的影响较大。在大洋内区, 垂直平均的耗散率与风生近惯性能量之间相关性很弱仅0.38, 略超过95%显著性水平,两者之间的线性拟合关系较不明显, 而且拟合系数远小于其它区域。

进一步分析耗散率与相应区域平均的风生近惯性能量的气候态的季节变化规律。从图7可以看到,除了大洋内区外上层海洋混合的季节变化与风生近惯性能量的位相一致, 冬季最强, 夏季最弱。子区域VI的耗散率却是冬季最强, 秋季最弱。如前所述, 本文用细尺度参数化方法估算得到的耗散率存在一定的误差, 与真实值εexa之间相差在4倍之内。为了检验以上得到的季节变化是否由估算误差导致, 采用Monte Carlo方法对冬春季平均与夏秋季平均的耗散率的比值R进行假设检验(Jinget al, 2013)。计算得到六个子区域中的R0值分别为1.54、1.51、1.32、1.40、1.62、1.56。假设估算的耗散率在区间[0.25εexa,4εexa]上均匀分布, 则R的概率密度函数可由Monte Carlo 方法模拟得到。如图8所示, 对于每个子区域,当εexa不存在季节变化时,R＞R0的概率不足5%。由此可见, 六个子区域中耗散率的季节变化都是可信的。

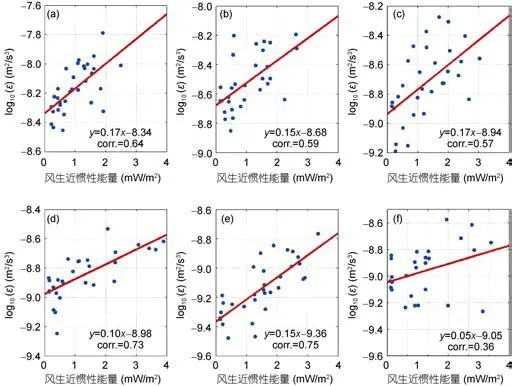
图6 对应图1中六个子区域垂直平均的耗散率与风生近惯性能量季节平均的线性拟合Fig.6 Linear regression between vertically averaged dissipation rates and seasonal-mean wind-induced near-inertial energy flux in six sub-regions as shown in Fig.1

图7 对应图1中六个子区域垂直平均的耗散率(a)及风生近惯性能量(b)的季节变化。Fig.7 Seasonal variations of vertically averaged dissipation rate (a) and wind-induced near-inertial energy (b) in the six sub-regions as shown in Fig.1

图8 利用Monte Carlo方法模拟的六个子区域中R的累计概率密度函数。红色虚线代表R0。Fig.8 Cumulative distribution functions of R-values derived with Monte Carlo method in the six sub-regions Red dashed lines represent R0.

这些结果进一步证实了在西北太平洋区域, 风应力对上层海洋混合具有重要的影响作用, 其影响深度最浅620m, 最深可达1740m。特别地, 在大洋内区, 上层海洋混合虽然也存在明显的季节变化, 但与风生近惯性能量的相关性较弱, 意味着混合还受到其它因素的影响。

3 讨论

本文利用历史水文观测剖面资料, 基于细尺度参数化方法, 分析了西北太平洋海区跨等密度面湍流混合的空间分布特征及风应力的影响深度, 结果表明:

耗散率的空间分布与地形粗糙度相似, 在地形粗糙的区域, 如日本海沟、伊豆-小笠原海脊处, 垂直平均的耗散率达到O(10–8m2/s3), 而在地形平坦的大洋内区, 垂直平均耗散率仅O(10–11m2/s3)。

耗散率呈现自西向东递减的趋势。在地形粗糙的伊豆-小笠原海脊附近, 东西约5°的范围内, 耗散率普遍较强。由于伊豆-小笠原海脊是西北太平洋一个重要的半日潮生成地, 而内潮能量的辐射距离可达O(1000km), 内潮与地形之间的强相互作用使得混合增强(Niwaet al, 2001; St. Laurentet al, 2001;Simmonset al, 2004)。海脊以西137°E处平坦地形上的强混合则是由次谐波不稳定性导致(Qiuet al,2012)。此外, 由于黑潮延伸体强流与粗糙地形相互作用, 地形对混合的影响向上可达2000—3000m(Kunzeet al, 2006)。

另外, 将研究区域划分为6个子区域(图1), 研究了风应力对混合季节变化的影响。结果发现, 在日本近岸区域I—V, 风生近惯性能量与上层的耗散率之间存在显著的正相关, 即当风输入的近惯性能量增加/减少时, 上层海洋的混合随之增强/减弱。同时风应力在不同区域的影响深度和程度也不同。在日本东南伊豆-小笠原海脊以东的子区域IV, 风应力的影响深度最深达1740m, 与耗散率的拟合系数较小为0.10;而在日本以南的子区域I, 风应力的影响深度最浅为620m, 拟合系数较大为0.17; 在日本海沟、伊豆小笠原海脊附近的子区域II、III、V, 风应力的影响深度约1000m, 拟合系数平均为0.16。而在大洋内区的子区域VI, 上层海洋的耗散率同样具有明显的季节变化, 且与风生近惯性能量之间存在一定的相关关系,但相关性较弱, 说明这里的混合还受到其它因素的影响。

Jing等(2013)发现夏威夷岛附近海域, 只有上层300—600m的混合具有明显的季节变化, 且与中尺度涡密切相关。在南大洋区域, 南极绕极流与粗糙地形相互作用也可为混合提供能量(Garabatoet al, 2004;Wuet al, 2011)。考虑到西北太平洋地区的中尺度涡活动频繁, 这里还存在很强的东向流黑潮延伸体, 因此中尺度涡、黑潮与内潮、地形相互作用等对于上层海洋混合及风应力的影响深度具有一定的影响。这些问题将在今后的文章中作进一步的探讨。

荆钊, 2012. 中尺度涡和风应力影响下的跨等密度面湍流混合低频变异. 青岛: 中国海洋大学硕士学位论文, 1—78

Alford M H, 2001. Internal swell generation: The spatial distribution of energy flux from the wind to mixed layer near-inertial motions. J Phys Oceanogr, 31(8): 2359—2368

Alford M H, 2003. Improved global maps and 54 year history of windwork on ocean inertial motions. Geophys Res Lett,30(8), 1424, doi: 10.1029/2002GL016614

Carter G S, Gregg M C, 2002. Intense, variable mixing near the head of Monterey Submarine Canyon. J Phys Oceanogr,32(11): 3145—3165

D’Asaro E A, 1985. The energy flux from the wind to near inertial motions in the mixed-layer. J Phys Oceanogr, 15(8):1043—1059

Garabato A C, Polzin K L, King B Aet al, 2004. Widespread intense turbulent mixing in the Southern Ocean. Science,303: 210—213

Gregg M C, 1987. Diapycnal mixing in the thermocline: A review. J Geophys Res, 92(C5): 5249—5286

Gregg M C, Kunze E, 1991. Shear and strain in Santa-Monica Basin. J Geophys Res, 96(C9): 16709—16719

Gregg M C, Sanford T B, Winkel D P, 2003. Reduced mixing from the breaking of internal waves in equatorial waters.Nature, 422, 513—515

Jing Z, Wu L X, 2010. Seasonal variation of turbulent diapycnal mixing in the northwestern Pacific stirred by wind stress,Geophys Res Lett, 37(23), L23604, doi: 10.1029/2010GL045418

Jing Z, Wu L X, Li Let al, 2011, Turbulent diapycnal mixing in the subtropical northwestern Pacific: Spatial-seasonal variations and role of eddies. J Geophys Res, 116, C10028,doi: 10.1029/2011jc007142

Jing Z, Wu L X, 2013. Low-Frequency Modulation of Turbulent Diapycnal Mixing by Anticyclonic Eddies Inferred from the HOT Time Series. J Phys Oceanogr, 43(4): 824—835

Kunze E, Firing E, Hummon J Met al, 2006. Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles. J Phys Oceanogr, 36(8): 1553—1576

Ledwell J R, Watson A J, Law C S, 1993. Evidence for slow mixing across the pycnocline from an open ocean tracer release experiment. Nature, 364: 701—703

Lilliefors H W, 1967. On Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. J Am Stat Assoc, 62(318): 399—402

Lueck R G, Mudge T D, 1997. Topographically induced mixing around a shallow seamount. Science, 276: 1831—1833

Munk W H, 1966. Abyssal recipes. Deep Sea Res, 13: 707—730

Nagasawa M, Niwa Y, Hibiya T, 2000. Spatial and temporal distribution of the wind-induced internal wave energy available for deep water mixing in the North Pacific. J Geophys Res, 105(C6): 13933—13943

Niwa Y, Hibiya T, 2001. Numerical study of the spatial distribution of the M2 internal tide in the Pacific Ocean. J Geophys Res, 106(C10): 22441—22449

Osborn T R, 1980. Estimates of the local-rate of vertical diffusion from dissipation measurements. J Phys Oceanogr,10(1): 83—89

Pollard R T, Millard R C, 1970. Comparison between observed and simulated wind-generated inertial oscillations. Deep Sea Res, 17: 813—821

Polzin K L, Oakey N S, Toole J Met al, 1996. Fine structure and microstructure characteristics across the northwest Atlantic subtropical front. J Geophys Res, 101(C6): 14111—14121

Polzin K L, Toole J M, Ledwell J Ret al, 1997. Spatial variability of turbulent mixing in the abyssal ocean. Science, 276: 93—96

Qiu B, Chen S M, Carter G S, 2012. Time-varying parametric subharmonic instability from repeat CTD surveys in the northwestern Pacific Ocean. J Geophys Res, 117, C09012,doi: 10.1029/2012JC007882

Simmons H L, Hallberg R W, Arbic B K, 2004. Internal wave generation in a global baroclinic tide model. Deep Sea Res,Part II, 51(25—26): 3043—3068

St. Laurent L, Toole J M, Schmitt R W, 2001. Buoyancy forcing by turbulence above rough topography in the abyssal Brazil Basin. J Phys Oceanogr, 31(12): 3476—3495

St. Laurent L, Garrett C, 2002. The role of internal tides in mixing the deep ocean. J Phys Oceanogr, 32(10): 2882—2899

Whalen C B, Talley L D, MacKinnon J A, 2012. Spatial and temporal variability of global ocean mixing inferred from Argo profiles, Geophys Res Lett (39), L18612, doi: 10.1029/2012GL053196

Waterman S, Naveira Garabato A C, Polzin K L, 2013. Internal waves and turbulence in the Antarctic Circumpolar Current.J Phys Oceanogr, 43(2): 259—282

Wu L X, Jing Z, Riser Set al, 2011. Seasonal and spatial variations of Southern Ocean diapycnal mixing from Argo profiling floats. Nat Geosci, 4: 363—366

Zhai X M, Greatbatch R J, Eden Cet al, 2009. On the Loss of Wind-Induced Near-Inertial Energy to Turbulent Mixing in the Upper Ocean. J Phys Oceanogr, 39(11): 3040—3045