多年冻土区低层建筑地下室土基的解冻计算
2014-03-19TerentyKornilovIgorRozhinEkaterinaKononovaDmitryGrigorievAyynaDanilova
Terenty A.Kornilov,Igor I.Rozhin,Ekaterina A.Kononova,Dmitry A.Grigoriev,Ayyna N.Danilova
(1.东北联邦大学工程技术学院,雅库茨克677000,俄罗斯;2.俄罗斯科学院西伯利亚分院石油和天然气研究所,雅库茨克677980,俄罗斯)
0 Introduction
In the conditions of permafrost one of the basic principles of construction is a preservation in a frozen condition of foundation of engineering constructions in the course of their maintenance which provides the stability,reliability and increases the service life of objects.For low-rise buildings of individual construction the surface basements are used primarily surface foundations bedding on filling,as a rule,without use of devices for airing of foundations and without sufficient thermal insulation of socle overlapping.As a result,there are cases of thawing of permafrost soil foundations,accordingly,the decrease of bearing ability of the basements and as a result,uneven deformations of buildings.
For relatively permafrost foundations of small width buildings,the thawing of foundations in operation when used foundation,capable to perceive uneven rainfall,for example,the cross-tape or slabby basements is allowed.It is as an alternative offered to provide and keep stability of permafrost soil for the entire period of house maintenance when using the superficial rigid basements on the adding condensed with gravel,at the expense of device of a heat-insulation layer under the house.
In the design and construction of buildings and constructions on frozen soil are widely used construction norms and rules,which are based on synthesis of long-term experience and on results of natural and laboratory experiments.However,they don't consider all variety of service conditions and types of constructed designs.At the same time computational experiment gives the chance to vary a wide range of entry conditions(meteorological data,temperature and heterogeneity of soil foundations,existence of thawed zones,salinity of ground waters),and also conditions of thermal influence of a construction on soil.These opportunities need to be used in cases,when it comes to the new types of construction designs which aren't reflected in standards.
Technological schemes and design features of constructions contacting with permafrost soils have to be considered surely at their design,construction and maintenance.Here the choice of correct decision is impossible without scientifically reasonable understanding of thermal processes occurring in system“frozen or thawed soil-engineering structure-environment”.For this purpose,it is necessary to know a temperature field of the soil foundation at any moment that gives the chance to predict soundly the stability of structures.However,it is difficult to set up such predictions for long term,since at the alternating temperature of the environment one has to solve the multifront Stefan's problem.The similar circumstance completely excludes possibility of analytical methods application.
With the development of computer facilities there is an opportunity to obtain rather authentic data on thermal processes the study of which in laboratory or natural conditions is very difficult,sometimes it is simply impossible and always demands considerable expenses of means and time.Moreover,results of such experiments practically aren't reproduced so they can't be used for long forecasting.This opportunity is realized in a method of computational experiment which essence is expressed by a triad“mathematical modelcomputational algorithm-the program realizing it”.
1 Statement of the problem and the method of solution
In this work by methods of mathematical modeling is investigated the thawing process of permafrost soil foundations of low-rise buildings with surface basements taking into account dynamics of temperature change of atmospheric air,total solar radiation,albedo of a surface,thickness of snow cover and coefficient of convective heat transfer of air.
In mathematical model the following assumptions were made:
1)heat transfer in the soil foundation is purely conductive;therefore,mass transfer processes are not taken into account in calculating the temperature field;
2)thermophysical characteristics of the layers of the natural foundation are assumed piecewise-constant for the thawed and frozen states,taking into account their slight variation in the temperature range considered;
3)phase transition of moisture occurs at a constant temperature(Tph-const)without the initial humidity(ω-const)and volume alteration.
The mathematical description of dynamics of a two-dimensional temperature field in soil foundation is executed on basis of the general statement of the Stefan problems.The model includes the quasi-linear heat conduction equation with the corresponding initial and boundary conditions,which taking into account multiple layers of the soil foundation has an appearance:
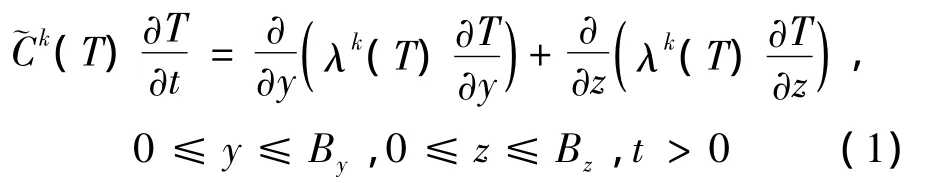
Here λk(T)and˜Ck(T)—coefficient of thermal conductivity and volumetric heat capacity k-of the soil foundation layer which are approximated as piecewiseconstant(smoothed)functions on temperature T in a vicinity of phase transition;y,z—longitudinal and vertical coordinates,t—time.The area of soil foundation by depth Bzand width By=By1+By2,where By1—half-width of building basement,By2—area size out of building basement is considered.
The numerical solution of problems of this kind is carried out by the methods based on the way,stated in the monograph[1].For this method authors of the works[2-3]developed an economicalfront-capturing difference scheme with the smoothing of discontinuous coefficients in the heat conductivity equation for temperature in the phase transition neighborhood.The schemes with a smoothing of coefficients are characterized by that the interphase boundary is not identified explicitly,the homogeneous difference schemes are used.The phase transition heat W=(qph+Tphcp)ρω is introduced by using the Dirac δ-function as a concentrated heat capacity in the heat capacity coefficient ˜Ck(T).In the last expression qph-specific heat of the phase transition,cp-the specific heat capacity of water,ρ-soil density.
Temperature field in an initial time point is set in the form of function depending only on vertical coordinate z:

On ground surface of soil foundation boundary condition of the third sort taking into account heat receipts at expense of radiation is set[4]:

where λ1—thermal conductivity of top layer of soil foundation,Ta—temperature of atmospheric air,αz—specified coefficient of heat transfer to upper bound of soil foundation—coefficient of heat transfer between ground surface and atmospheric air which depends on wind velocity υa[5],Qsr—total solar radiation,A—surface albedo.In settlement area where there is a building basement thermal radiation is neglected,that is at 0≤y≤By1is accepted Qsr=0.
All layers of building basement,and also snow cover out of building are considered as thermal resistance in specified coefficient of heat transfer αz:
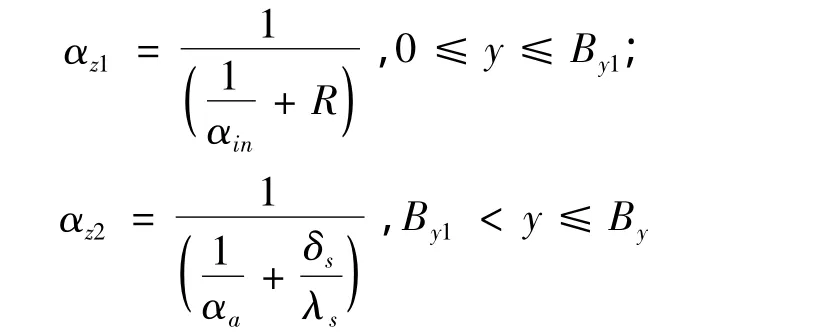
where αin—coefficient of heat transfer between inner air and floor surface of building;R—general thermal resistance of the whole building basement design(socle overlapping);δs—thickness of snow cover.True heat conductivity(without mass transfer)of snow cover λs(W/m·℃)depends on density ρs(g/sm3)[4]:On borders of soil foundation layers conditions of ideal thermal contact,i.e.boundary conditions of the fourth sort(equality of temperatures and heat fluxes),are accepted.
Also we accept a condition of symmetry and an equality condition to zero heat fluxes on sufficient removal from building borders:
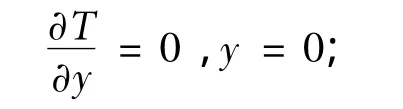
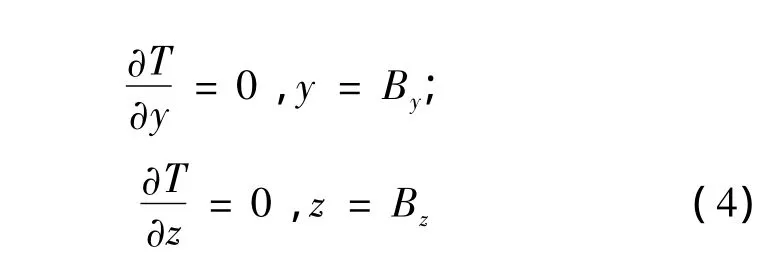
In the developed mathematical model of two-dimensional section of building basement with heat-insulating material are considered:dynamics of the cyclic change of atmospheric air temperature;the dependence coefficient of heat transfer between ground surface and atmospheric air on wind velocity.Besides,out of residential building change of snow cover,influence of total solar radiation and albedo of ground surface are considered.
The problem(1)-(4)is solved by the finitedifference method using the transverse-longitudinal scheme(total approximation)[6-7].Thus the effective calculation of the two-dimensional problem is based on the method of splitting-up by spatial coordinates using the scheme of variable directions[8-9]and implicit methods to provide stability of the obtained one-dimensional problems.The resulting difference problem being nonlinear,its solution is found by the method of simple iterations and of sweeping(the tridiagonal inversion)algorithm.
2 Results of the computational experiment
Calculations are executed at basic data,which include:data on design of socle overlapping,on material structure of soil foundation and their heat and physical characteristics,given to thermometry,sizes of studied basement of building.Missing data(average monthly values of air temperature,velocity of a wind,total solar radiation and albedo of ground surface,and also each decade values of thickness and density of snow cover)were taken from the published reference or scientific books[4,10-14].
Natural data of temperatures on depth are provided in Table 1 and Table 2 for permafrost-soil conditions of Namtsy village and Yakutsk City,which are accepted to entry conditions.Physical properties of multilayered soil foundation,where h-power of soil layer,and lower indexes mean are given in Table 3 and Table 4: th-thawed,f-frozen.These data are obtained on the basis of complex construction researches,and heat and physical properties of soil are accepted on standard values.
Calculations of thermal mode of soil foundation under the building were carried out at following entrance data:qph=334 400 J/kg,cp=4 184 J/(kg ·℃),By=20 m;Bz=15 m,αin=8.7 W/(m2(℃).Temperature in a residential building is constant and equals to Ta=20℃.The variation of value of general thermal resistance of socle design is accepted for more frequently applied structure of basement part of building(dumping from PGS-300 mm,rubble-50 mm,a heat-insulation layer from PSB-S,sand-50 mm,air layer,board flooring-32 mm).

Table 1 Temperatures on depth of soil foundation in the middle of October(Namtsy)
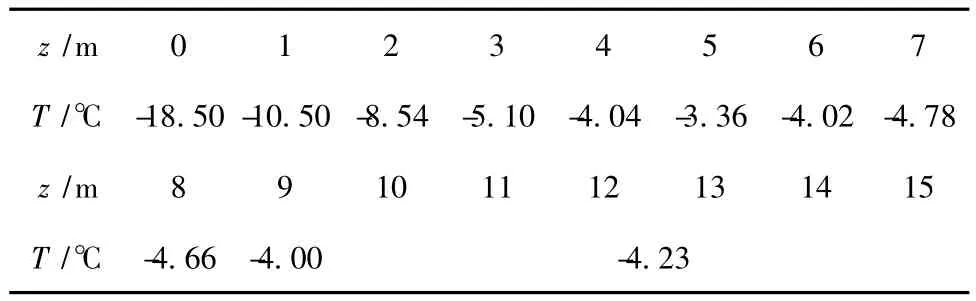
Table 2 Temperatures on depth of soil foundation in the middle of March(Yakutsk)

Table 3 Characteristics of layers of soil foundation for conditions of Namtsy

Continued table 3

Table 4 Characteristics of layers of soil foundation for conditions of Yakutsk
In computational experiment was studied the influence of base design and width of low-rise buildings on dynamics of change of thawing bowl of soil under the building.Temperature fields of soil foundation and various configurations of thawing bowl depending on building sizes,thermal resistance of socle overlapping and permafrost-soil conditions in various time points are received.
Fig.1 shows dynamics of change of thawing bowl of soil foundation under the building depending on value of general thermal resistance of basement,and Fig.2-depending on sizes of building basement.In these figures S is thawing depth.
In Fig.3-Fig.6 configurations of thawing bowl under buildings where figures at curves correspond to years of maintenance of buildings are presented.The analysis of results showed that with increase in thermal resistance of buildings basements,that is,with increase in thickness of heater and air layer penetration of thermal indignations into soil is slowed down that promotes reduction of depth of thawing of soil foundation and increases its thermal stability.Moreover,from Fig.1,and Fig.4 follows Fig.3 that relation of depths of soil thawing on axis of symmetry of building in 50 years of maintenance in inverse proportion to relation of thermal resistance of basement.
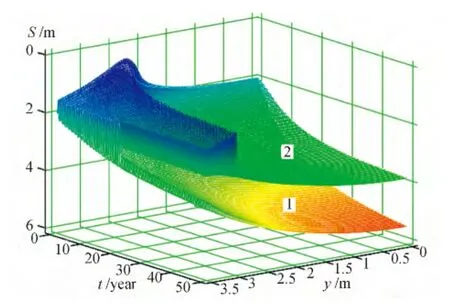
Fig.1 Changes of thawing bowl of soil foundation under building by width and time at building half-width of By1=3.5 m(Namtsy):1-R=5.13 m2·K/W;2-R= 7.44 m·2K/W
The increase in width of building conducts,as one would expect,to increase in depth of thawing that is well visible from Fig.2,and also from Fig.4 and Fig.5.Physically this results from fact that with increase in width of building penetration of temperature wave from atmospheric air to foundation center(symmetry axis)is at a loss,that is,here thawing bowl is formed only under influence of thermal influence of construction.

Fig.2 Change of thawing bowl of soil foundation under building by width and time at thermal resistanceof R= 7.44 m2(K/W(Namtsy):1-By1=3.5 m;2-By1=7.0 m;3-By1=10.0 m
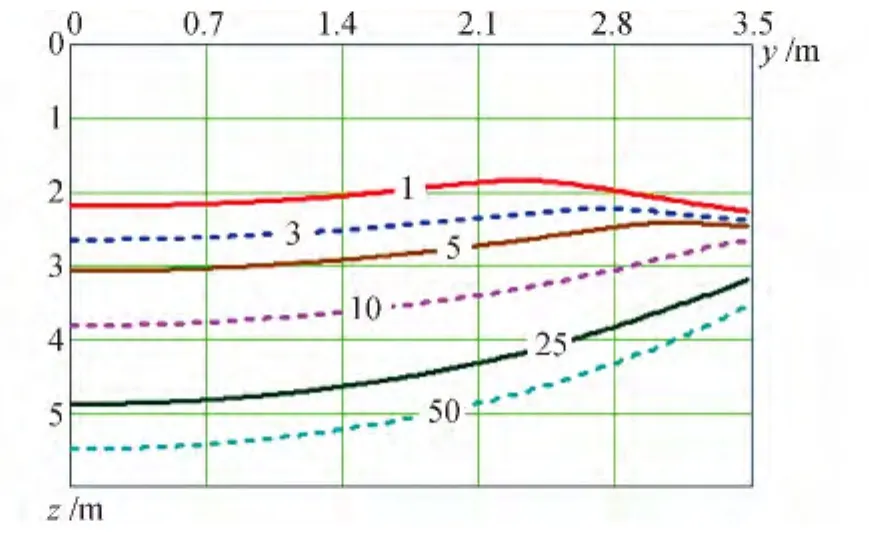
Fig.3 Configurations of thawing bowl under building,width of B=7 m and thermal resistance of R=5.13 m2·K/W(Namtsy)
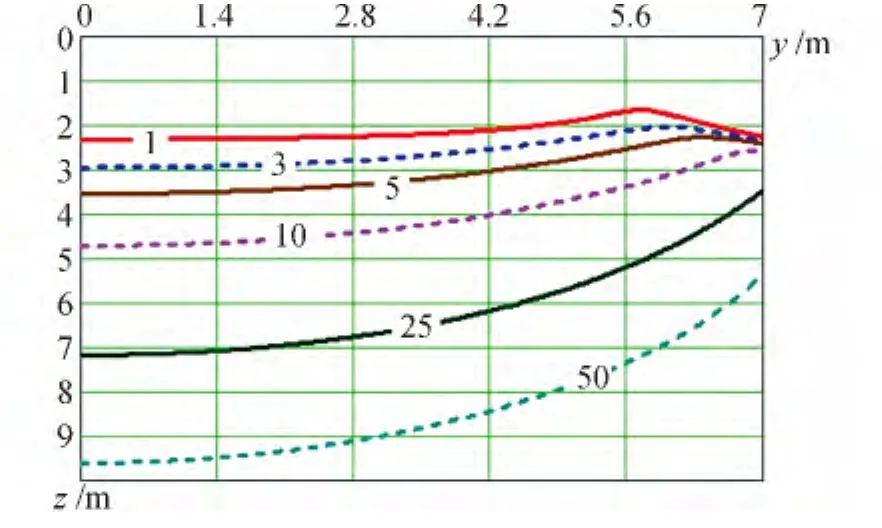
Fig.4 Configurations of thawing bowl under building,width of B=14 m and thermal resistance of R=7.44 m2·K/W(Namtsy)
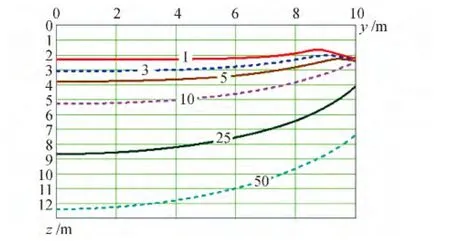
Fig.5 Configurations of thawing bowl under building,width of B=20 m and thermal resistance of R=7.44 m2·K/W(Namtsy)
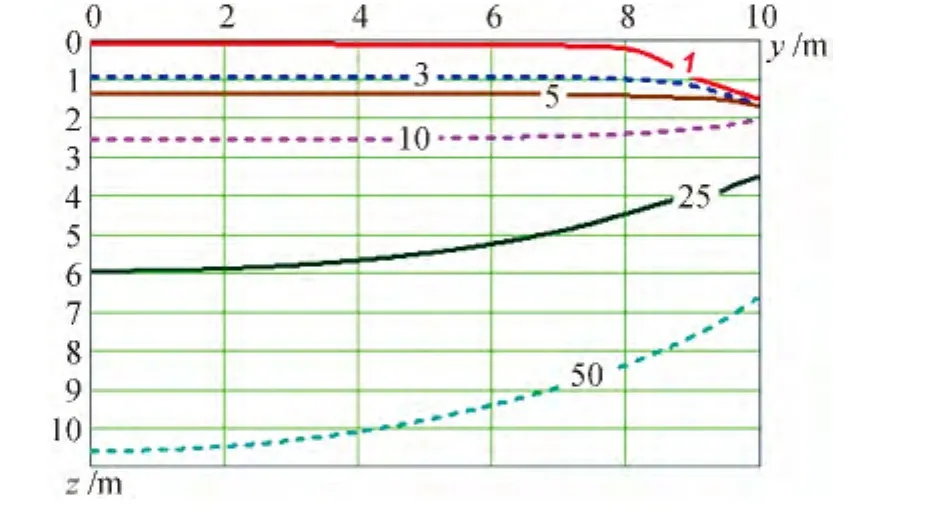
Fig.6 Configurations of thawing bowl under building,width B=20 m and thermal resistance of R=7.44 m2· K/W(Yakutsk)
Influence like soil can be estimated,having compared results ofcalculations presented in Fig.5 (Namtsy)and Fig.6(Yakutsk).From these drawings follows that thawing depth for conditions of Yakutsk is less,than for conditions of Namtsy,in spite of fact that in the first case soil is damper,less dense and heatconducting.Here major importance has that fact that at the beginning of building maintenance in Yakutsk the soil foundation was in a frozen state,and temperature of freezing of soil because of salinity of steam space always is lower than 0℃,as defined a difference in depth of thawing approximately in 2 m.
Results of computational experiment are compared to calculations for joint venture 25.13330.2012.Estimated two sizes:thawing depth on center of building and thawing depth on periphery.Results of comparison are presented in Table 5(Namtsy)and Table 6(Yakutsk),and for two combinations of base design and building width,but for different building sites-in Fig.7 and Fig.8.Previously we will notice that except distinctions in types of soil for Namtsy and Yakutsk,in the first case at the initial moment already there was a thawed layer of 2 m in depth that don't consider existing rules.

Table 5 Comparison of calculated depths of thawing under building in the conditions of Namtsy

Continued table 5

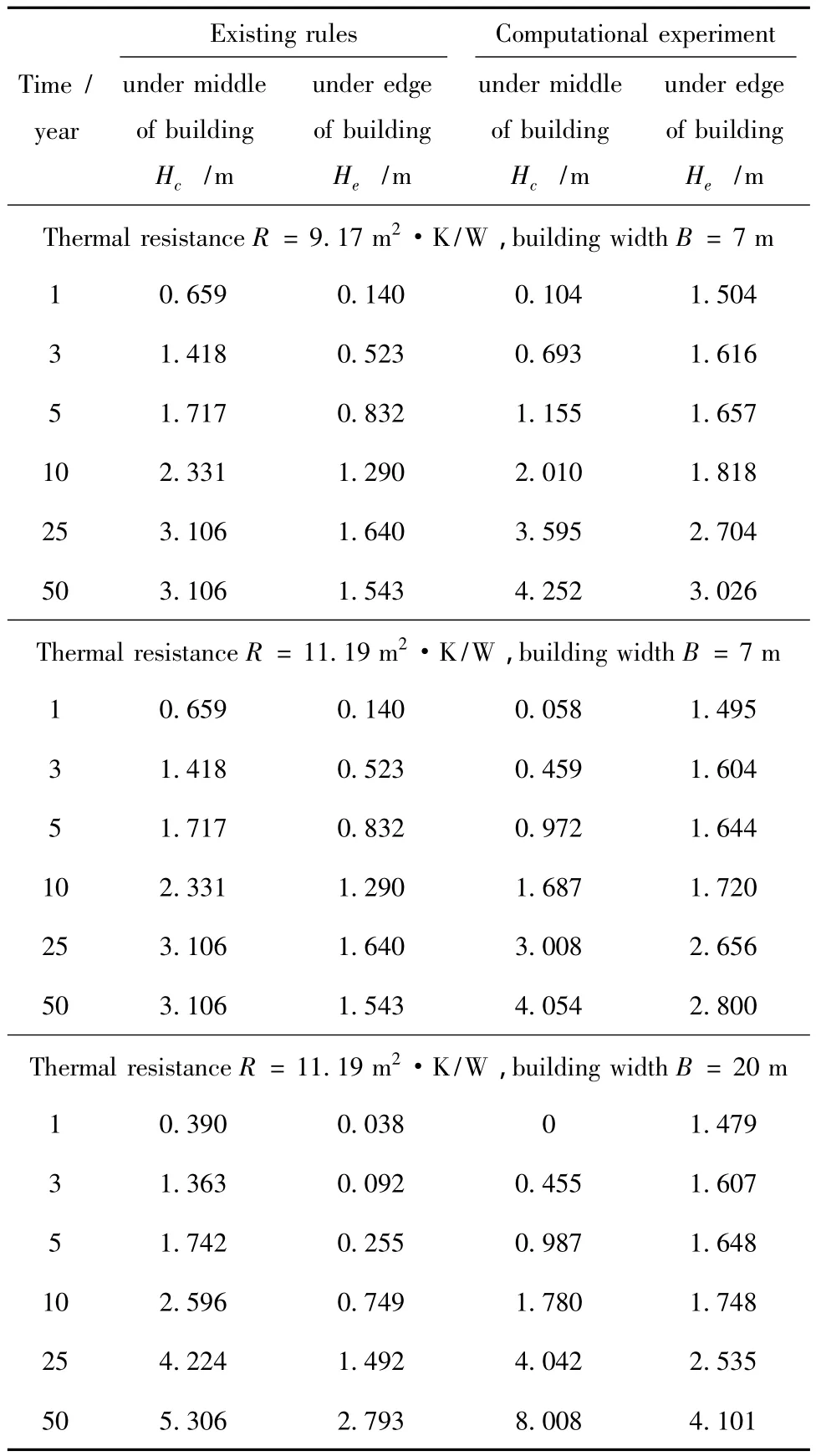
Table 6 Comparison of calculated depths of thawing under building in the conditions of Yakutsk
Continued table 6
The main conclusion which follows from results presented in these tables,is that depth of soil thawing,calculated on existing rules,doesn't depend on thermal resistance of socle overlapping.
For building site of Yakutsk of distinction for long terms of building maintenance of are more considerable,than for Namtsy(compare curves in Fig.7 and Fig.8).Besides here,as well as in case of Namtsy,existing rules give identical size of thawing for various thermal resistance of basement(see Table 6),and at small terms of maintenance(1 year and 5 years)these distinctions not only quantitative,but also qualitative (see curves 1 and 5 in Fig.7 and Fig.8).Partially these divergences of sizes of thawing can be explained that in SP 25.13330.2012 initial condition of thawing bowl(prior to building maintenance)and cyclic change of temperature of atmospheric air aren't considered,and all physical characteristics of soil foundation are averaged on depth,however to size of thermal resistance is rational to explain tolerance of results of calculation it is impossible.
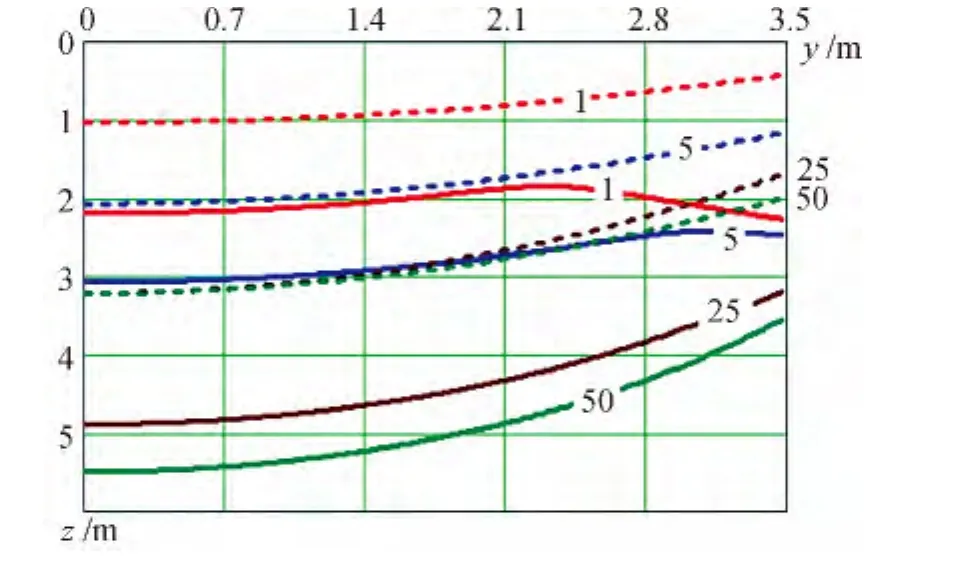
Fig.7 Comparison of results of calculation of thawing bowl,existing rules received by technique(dot curves)and numerical modeling (continuous curves)at B=7 m,R=5.13 m2 (K/W(October,Namtsy)

Fig.8 Comparison of results of calculation of thawing bowl,existing rules received by technique(dot curves)and numerical modeling (continuous curves)at B=20 m,R=7.44 m2 (K/W(April,Yakutsk)
3 Conclusions
The general conclusion which follows from the comparative analysis of results of calculation:technique of existing rules isn't suitable for determination of depth of thawing of soil under buildings of small sizes and(or)with big warming of socle part.
[1] Tikhonov A N,Samarsky A A.Equations of the mathematical physics[M],5th edition.Moscow:Nauka,1977.
[2] Samarsky A A,Moiseenko B D.Economical shock-capturing scheme for the multidimensional Stefan problems[J].Comput.Math.and Math.Phys.1965,5(5):816-827.
[3] Budak B M,Solovieva E N,Uspensky A B.Difference method with coefficients smoothing for solving the Stefan problem[J].Comp.Math.and Math.Phys.,1965,5(5):828-840.
[4] Pavlov A V.Soil heat transfer with atmosphere in northern and middle atitudes of USSR territory[M].Yakutsk:Yakut book publishing house,1975.
[5] Porkhayev G V,Shchelokov V K.Forecasting of temperature mode of permafrost soil in built-up territories[M].Leningrad:Stroyizdat,1980.
[6] Samarsky A A.Introduction to the theory of difference schemes[M].Moscow:Nauka,1971.
[7] Kalitkin N N.Numerical methods[M].Moscow:Nauka,1978.
[8] Yanenko N N.The subincremental method of solving the multidimensional problems of the mathematical physics[M].Novosibirsk:Nauka,1967.
[9] Yanenko N N.The method of fractional steps[M].New York: Springer-Verlag,1971.
[10]Gavrilova M K.Climate of the Central Yakutia[M].Yakutsk: Yakut book publishing house,1973.
[11]SNIP(Building Norms and Rules)II-3-79*.Construction heating engineer[M].Moscow:State Constr.of Russia,1998.
[12]SNIP(Building Norms and Rules)23-01-99.Construction climatology[M].Moscow:State Constr.of Russia,2000.
[13]Fedorov A N,Maksimov T K,Gavrilyev P P,et al.Spasskaya cave:Complex researches of permafrost landscapes[M].Yakutsk: Publishing house of Permafrost Institute SB RAS,2006.
[14]SP(Set of Rules)25.13330.2012.Bases and foundations on permafrost soil[M].Moscow,2012.
