地下种子冷冻库的温度调控

Elena Romanova，Alexander Kurilko，Yury Khokholov

(俄罗斯科学院西伯利亚分院北极矿业研究所，雅库茨克677980，俄罗斯)

0 Introduction

Nowadays around the world，including regions of cryolithozone，for placement of various objects of warehouse appointmenta keen interest in use of subsoil and the available underground developed space is observed.Climatic conditions of the North，existence of potent thickness of longstanding frozen rocks and unlimited stocks of cold are favorable for construction of underground cold-storage plant and cryostorages.

The modern level of projection，existence of highperformance technologies allow to develop bankable projects and to conduct construction of power efficient underground structures of any sizes and complexity，including underground cryostorages of seed reserves.

One of the major questions，defining energy efficiency of operation of underground cryostorage，is a rational use of natural cold，both atmospheric，and accumulated by the rocks，minimizing energy consumption on development of artifical cold.

The principle of long-term steady maintaining of the demanded temperature of storage has to be the basis for regulation of a temperature mode of underground cryostorage of seed reserves due to rational use of natural cold，both atmospheric，and accumulated by rocks.

1 Mathematical modeling of heat exchange processes in the underground cryostorage

The three-dimensional mathematical model of heat exchange processes is developed to forecast a temperature mode of a storage cave of underground cryostorage in storage caves of the underground cryostorage，considering climatic conditions(a sunshine，dynamics of change of temperature of free air，depth of snow，wind speed)，design features(the geometrical sizes and depth of an underlay of a chamber，thermal properties and the geometrical sizes of thermal insulation of surfaces of a chamber and thermal insulation of a daylight surface over a chamber)and a technological external environment(a ventilation mode，a operating regime of heating(refrigerating)installations，a mode of loading by a biomaterial).Its calculated area is presented in Fig.1.

The chamber represents the stretched horizontal mine located at the given depth from a surface of the earth，having a rectangular transverse section，and it is set by the following geometrical parameters:width，height and length.For maintaining of the demanded temperature of storage in a chamber express refrigerator sets are used.For decrease in energy consumption on development of artifiial cold in the first years of operation the preliminary winter cold charging which is encapsulating in giving by the fan of cold free air is carried out.During cryostorage operation a ventilation of a chamber is not carried out.

Fig.1 The calculation area Ω，where x1，xmax，y1，y2，ymax，zmaxare the coordinates of its borders

The task of calculation of a temperature mode of a chamber of underground cryostorage consists in definition on any instant:

-air temperature distributions in a chamber;

-temperature distributions in the massif of rocks round a chamber;

When developing mathematical model of the thermal processes happening in a chamber and in the rock massif，surrounding it，the following simplifying assumptions are accepted:

1)air in development mixes upwell;air temperature during ventilation is averaged on a transverse section and when ventilation is disconnected，it is averaged on all volume of development;

2)heatinputs to a chamber enter only from the environmental mountain.

The mathematical model for the solution of an objective is under construction in a routine rectangular (Cartesian)frame(x，y，z).The studied temperature field at present time of t is determined by temperature distribution by the massif of rocks，i.e.function T=T (x，y，z，t).

The calculated area for containing rocks has the compoundshape in the form of the hollow half-space limited to a daylight surface.The form and the sizes of a cavity are defined by geometrical parameters of the chamber having a rectangular transverse section.Let's carry out the following simplifying actions over a calculated area.First，in connection with difficulties of finding of the numerical decision in the infinite area we will apply the approach based on ideas of an integral method and consisting in introduction of borders of thermal influence.Secondly，as the problem of definition of a temperature field of the massif of rocks is symmetric，it is possible to consider it for a half of calculated area.The final form of spatial calculated domain is given in Fig.1.

In the massif of rocks we will describe process of distribution of heat by means of a nonstationary heat conduction equation taking into account phase changes of moisture［1］.The solution of the equation is looked for in Q={(x，y，z，t)|((x，y，z)，0＜t＜tmax}，i.e.:

where Ceff—effective heat capacity，J/(m3·K);λ—heat conductivity coefficient of rock，W/(m·K).

The accounting of warmth of phase change is equivalent to a task of an effective heat capacity:

where C(T)—is a specific heat per unit volume of rock，J/(m3·K);Lph—warmth of phase change of moisture，J/kg;W—humidity of rocks，fractions of a unit;ρ—density of rocks，kg/m3;T*—melting point (freezing)of water in rock，C°，δ—Dirac function; μ—number of the front of phase change(μ=1，…，μ0).

Thermal capacity and heat conductivity coefficients arediffused and also have a form of:

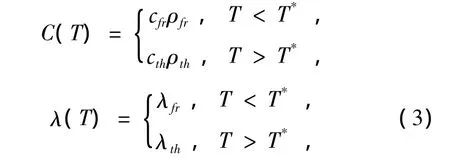
where cfr，ρfr，λfr(cth，ρth，λth)—specific heat，J/ (kg·K)，density，kg/m3，a thermal conductivity， W/(m·K)for frozen(thawed)rocks，respectively.

Introduction of an efficient thermal capacity in a heat conduction equation allows to construct efficient computing procedures of numerical problem solving with phase changes.

For definition of a temperature field of T(x，y，z，t)besides a heat conduction equation it is necessary to formulate padding(closing)ratios:boundary and starting conditions.

On border consisting of surfaces，limiting a chamber Bch，boundary condition third type simulating heat convection is set:

where ∂/∂nBch—outwardnormaltotheboundary Bch; Tair—air temperature in the chamber，℃;α—heattransfer coefficient through walls of the chamber，W/ (m2·K).

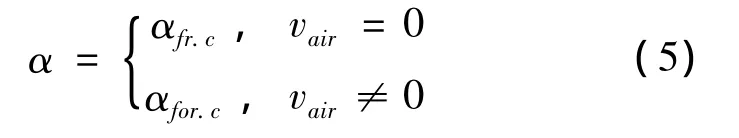
where αfr.c，αfor.c—heat-transfer coefficients through chamber walls in a mode of the free convection(W/ (m2·K))，in the conditions of forced convection (W/(m2·K))，respectively;vair— the speed of a ventilating stream，m/s.

Heat exchange condition on the border corresponding to a day surface，Bd.surf，taking note of a radiant energy of the sun［2］:

where Tatm.air—temperature ofatmosphericair，℃;∂/∂nBd.surf—an external normal to border Bd.surf;day surface;αd.surf—coefficient of heat convection of a surface of the soil，W/(m2·К);Qs—a cooperative sunshine，W/m2;A—albedo of a surface，a unit fraction.

The coefficient of heat exchange of a surface of the soil taking into account snow cover is determined by a formula［3］: where—coefficient of heat exchange of a surface of the soil in the absence of snow cover，W/(m2· K);δsn—thickness of snow cover，m;λsn—a heating conductivity of snow，W/(m·K).

On border of heating influence，Btherm.infl，on a plane of symmetry of Bsymand on the platitudes limiting area longwise of development，Bl.chthe boundary condition of the second sort is set:

where∂/∂nBtherm.infl，∂/∂nBsymand∂/∂nBl.chare the external normals in relation to area to borders of Btherm.infl，Bsymand Bl.ch，respectively.

In anstart time initial distribution of temperature of rocks is set:

During a preliminary winter cold charging on a chamber entrancein a particular volume fresh cold air is supplied it formes a ventilating stream and it moves longwise chambers.And during cryostorage operation the entrance is isolated from intake of fresh air.When air temperature in a chamber becomes higher than required temperature，refrigerator sets join.

The energy conservation equation in a chamber when driving air has a form:

where cair，αair，ρair—specific heat(J/(kg·K))，density(kg/m3)，a thermal conductivity(W/(m· k))air，respectively;ωair—the speed of air，m/s; the term ωair∂Tair/∂z defines temperature change due to convective diffusion of heat.

Temperature on an entrance to a chamber during ventilationis equal:

In anstart time initial distributions of air temperature longwise chambers are set:

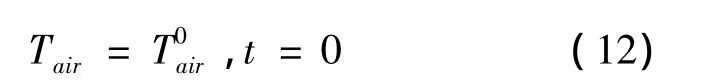
While operating time of refrigerator sets average air temperature is equal in a chamber to the demanded temperature of storage of biomass

In solving the problem of definition of a temperature field of the massif of the rocks surrounding a chamber，drawing up forecasts for the long term becomes complicated that at sign-variable environment temperature for definition of a temperature field of the rocks containing a cold storage room，it is necessary to solve a multifront problem of the Stefan，i.e.a nonlinear boundary value problem for the parabolic equations with in explosive coefficients on unknown surfaces.Thereby possibility of application of analytical methods is completely excluded.Under these circumstances numerical methods are efficient.The most suitable for the numerical solution of many-dimensional tasks of the Stefan in the presence of several it is nonmonotone moving fronts is the method of the through account of Samarskogo-Moiseenko［4］.The main advantages of this method are logical simplicity and possibility of application of a big step on time［5］.

2 Discussion

As a result of numerical realization of mathematical model the main consistent patterns of formation of a temperature mode of underground cryostorage are determined and its design data providing long-term storage of seeds are proved.We will give calculation of heating loads of the refrigerating appliances supporting a necessary temperature mode as an example(－8 C°)，at various modes of a winter cold charging and depths of an underlay of the storage cave，made with use of the developed technique.

Calculations are carried out for climatic conditions of Yakutsk.Storage cave sizes:width is 6 m，height is 4 m，length is 50 m.Operational year begins in the fall with approach of the negative temperature of free air(the end of September).Before commisioning it is carried out primary freezing chambers by natural(atmospheric)cold by the forced ventilation.During operation the winter cold charging of a chamber is not carried out，the necessary temperature of storage(－8 C°)it is supported by means of refrigerator sets.

The power of refrigerator sets necessary for maintaining of the demanded air temperature in a cold storage room，pays off in size of heat input to a chamber.

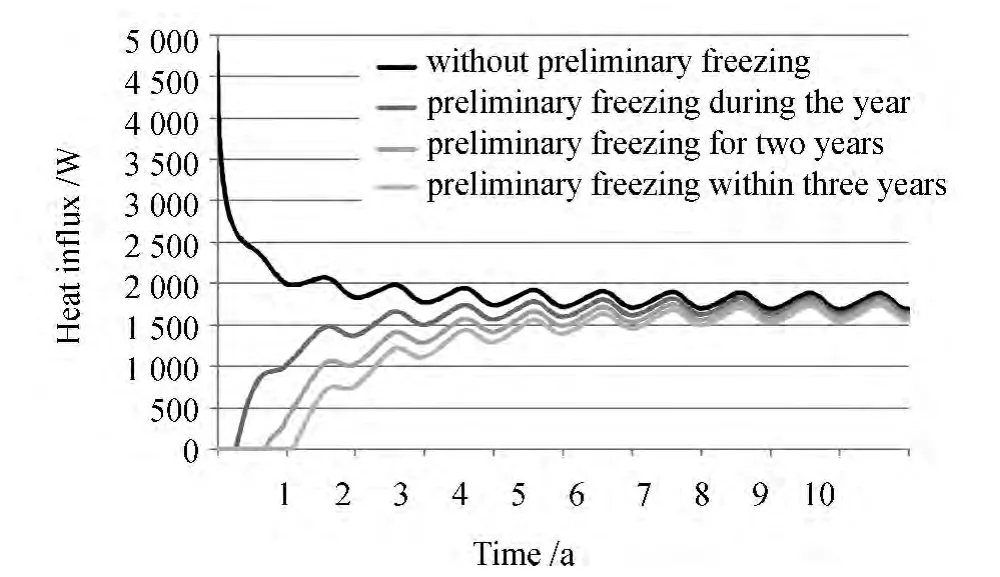
Fig.2 Heat influxes into the chamber at different modes of commissioning

In Fig.2 dynamics of changes of heat inputs to a chamber for the first 10 years of operation is presented at different modes of commisioning:without preliminary freezing and with freezing within several years.Forcing of free air is carried out within four most cold months(November，December，January，February) with intensity of 15 m3/s.

Apparently from schedules，preliminary freeing promotes the fissile deepfreezing of the containing rock massif，respectively postpones the time of inclusion of refrigerator sets and significantly reduces heating loads of them that is most brightly expressed in the first year of operation.Year freezing reduces energy consumption by development of simulated cold for the first year of operation by 5 times，biennial-by 59 times.Three-year freezing the inventory more than for a year postpones the time of inclusion refrigerating.

Fig.3 shows theinfluence of seasonal temperature variation of free air through a chamber roof on heating loads of refrigeratingappliances.Apparentlyfrom schedules，storage cave deepening from 10 m to 20 m reduces heat inputs by the size from 43%(1 year of operation)to 18%(the 10th year of operation).Respectively the required power of refrigerators and energy consumption on development of simulated cold decreases.

Fig.3 Heat inputs to an underground chamber with different depths of an underlay from a terrestrial surface

Numerical realization of the developed three-dimensional model allows to investigate heat exchange influence on a daylight surface on heating load of the refrigerating appliances supporting a stable temperature mode in a chamber.

Test calculations for an assessment of influence of various options of management by heat exchange on a daylight surface on heating load of refrigerating appliances are carried out.

In Fig.4 dynamics of changes of heat inputs to a chamber for the first 10 years of operation is presented at different options of management by heat exchange on a daylight surface:removal of snow and heating insulation use in operation summertime.Heating insulation 0.2 m thick and with coefficient of heating insulation of 0.1 W/(mK)is considered.The daylight surface over a chamber is heat-insulated from spring to fall when temperature of free air is higher－8 C°.

Calculations showed that during removal of snow by winter on a day surface heating loads of refrigerating appliances decrease as much as possible(in the 10th year of operation)by 48%and if thus to protect a daylight surface from a sunshine，reduction of heating loadings reaches 54%.Padding use in a warm season of heating insulation on a daylight surface over a chamber brings decrease in heating loads of refrigerating appliances to 61%.

Results of the conducted numerical researches on mathematical model confirm possibility of accumulation of cold progressing from year to year with the rock mas-sif containing developments of underground cryostorage，at correctly organized freezing by atmospheric cold in winter time.

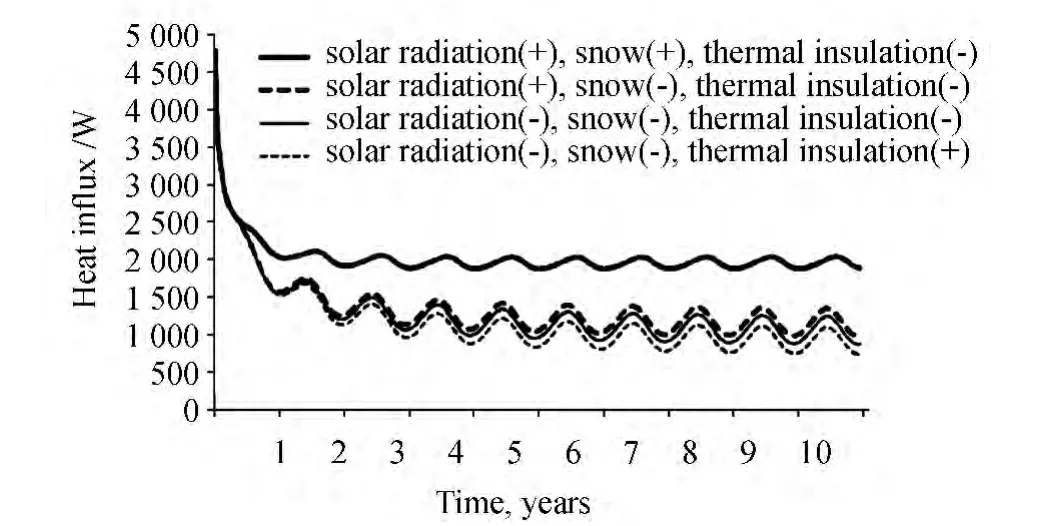
Fig.4 Heat inputs to a chamber at different options of management of heat exchange on a daylight surface，where(－)lack of parameter of management of heat exchange，(+)presence of parameter of management by heat exchange.

The most efficient and reliable way of regulation of a heating conditions of underground cryostorage is the combined way at which the atmospheric cold and refrigerators is used in the winter in the summer.When using this way，in the first years of operation of again constructed storage it is possible to lower considerably energy consumption on development of simulated cold.

3 Conclusions

Thedeveloped three-dimensionalmathematical model allows to establish regularities of formation of a temperature mode of underground cryostorage depending on its various technological and design data.

Researches showed that by management of heat exchange on a daylight surface it is possible to achieve essential reduction of heating loads of the refrigerating appliances providing a stable temperature mode of underground cryostorage.

For increase of energy efficiency of operation of underground cryostorage it is recommended:

1)to exempt a day surface from snow cover over a chamber in the winter;

2)to heat-insulate a day surface in the greatest possible way from influence of free air in a warm season (when temperature of free air is higher than temperature of storage of biomass)over a chamber;

3)to protect a day surface from a sunshineover a chamber.

［1］ Samarsky A，Vabishchevich P.Computing heat transfer［M］.Moscow:Editorial of URSS，2003:66-72.

［2］ Izakson V，Samokhin A，Petrov E，et al.Questions of stability of exposures mnogoletnemerzlykh of breeds［M］.Novosibirsk:Siberian Publishing House“Science”，1994.

［3］ Galkin A，Khokholov Y.Heat-retaining developments［M］.Novosibirsk:Siberian Publishing House“Science”，1992.

［4］ Samarsky A，Moiseenko B.The economic scheme of the through account for a many-dimensional problem of Stefan［J］.Journal of Computational Mathematics and Mathematical Physics，1965，(5):816-827.

［5］ Popov F.Computing methods of engineering geocryology［Z］，1995.