冻土的耐久性分析

Alexandr Konovalov

(秋明国立石油天然气大学，秋明625003，俄罗斯)

0 Introduction

Communication between the particles of the frozen ground，depends on the proximity of their temperature t (℃)to the melting temperature tml，which can be plastic(“melting”)near tmland fragile(“sublimation”) away from t=tml［1-2］.

The energy of plastic ties equal to the specific heat of melting(crystallization)Qml，fragile-specific heat of sublimation Qs.Different types of links particles of frozen soil are defined and different mechanisms of its destruction are difined.

Plastic destruction is the deformation of frozen body(its connections particles)，with a gradual transition in flowing state.This state is fixed on achieving the approximate equality jl≈ jml≈ 0，083… 0，12 (here jml-relative deformation of the thawing of frozen soil，jl-relative limit of deformation).Sublimation corresponds to a complete rupture of atomic bond，educa-tion at its place of“emptiness”，when the relative deformation is the highest-jl≈js≈1(ice-1，existing at t＞ －22℃;values jsand Qs，and more jml≈jland Qmlroughly 12 times［1，3］).At the macro level such deformation is local，and is confined to areas with weak links hub voltage(micro-cracks，defects of structure…).Unnoticed by an observer it develops in the form of domestic fissuring in the direction of compression and fixeds at rapid disintegration of the body.Purpose of work is to identify the conditions under which prevailed plastic or brittle fracture.

1 Calculation models

Formula durability τdof plastic permafrost is［Konovalov，2009，2012］:

where P is pressure(load)，Pm.mlis maximum(conditionally instantaneous)strength plastic-frozen soil，appropriate minimum durability τo.

Durability of frozen soil with a low melting temperature is determined by the well-known formula［4］，given by the author to mind［1-2］:

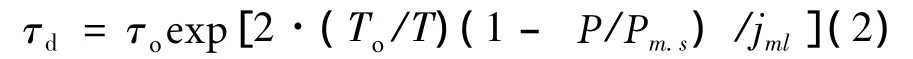
where P is pressure(load)，Pm.mlis maximum(conditionally instantaneous)strength，Pm.sis maximum (conditionally instantaneous)strength fragile(brittle)-frozen soil，appropriate minimum durability τo.

The maximum pressure，that the equilibrium minimum durability:Pm=Pm.mlthe plastic-frozen soil and Pm=Pm.mlthe fragile-frozen，in both cases is determined by the equation of Clapeyron–Clausius.

In this case it is substituted:the current temperature of the frozen ground，t＜tml，and the corresponding volumetric heat of phase transitions(Lml= Qml/ Vsl，where Vslis the specific volume of a solid phase or Ls=12 Lml)with dimension of pressure，and deformation(jmlor js=12 jml).Replacing the index when these values shared index，f，we obtain a general expression for the maximum(instant)strength.

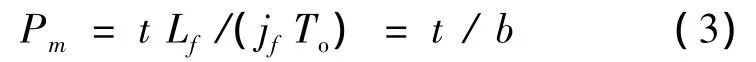
Substituting(3)into(1)，after conversion，we obtain the equation for determining the durability of the body，as a function of temperature and pressure or temperature only:

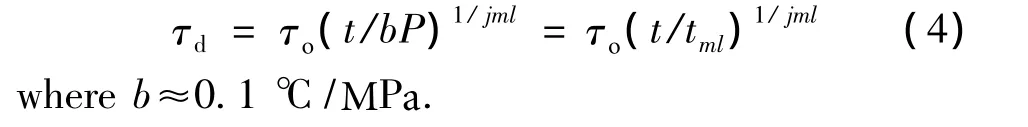
When τd=τoexpression(4)is transformed into an equation for the phase equilibrium.That is，the formula(4)is non-stationary modification equations of Clapeyron-Clausius.Other options formulas(4)and the examples of good convergence of the calculated and actual(experimental)values of durability are given in works［1-3］.It is also shown，that the validity of the formula(4)is not broken，if instead of instantaneous values of durability and strength to take，as a baseline (initial)and giving the first measured couples P1and τ1status of conditionally-instant durability and strength.This greatly simplifies the evaluation of the durability of the material.

Another major factor in lowering the phase transition temperature tfis soil salinity.Fig.1 shows the relative phase transition temperature θ=tf/tmfrom the relative pressure H=P/Peand relative concentration of the pore solution G=K/Ke

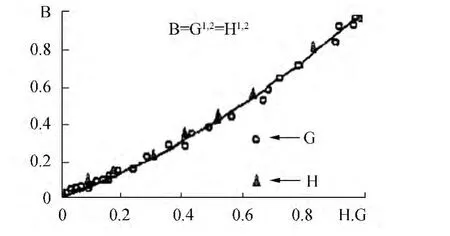
Fig.1 The dependence of θ from H=P/Peand G=K/Ke

Here tmrefers to minimum temperature of the existence of ice-1 in evaluating the influence of pressure (tm≈－22℃)or eutectic temperature(tm≈ te)solution of this salt in evaluating the influence of salinity; Ke-concentration of eutectic.Eutectic temperature and concentrations are given in Table 1.

Table 1 Eutectic concentration and temperature common salts

Judging by Fig.1 dependence θ from both factors are identical.It allows you to express salinity via the equivalent pressure

which for the accounting of joint influence of pressure and salinity in temperature freezing is added to the pressure value in the formula(3):

where∑(К/Кe.)is the sum of the relative concentrations of each of salt.The formula(6)is valid under the condition，when the sum of the relative pressure and concentrations of less than 1.For real soil and pore moisture which is a weakly concentrated solutions，this condition is always running.

Convert formulas(1)and(2)to comparable mind:

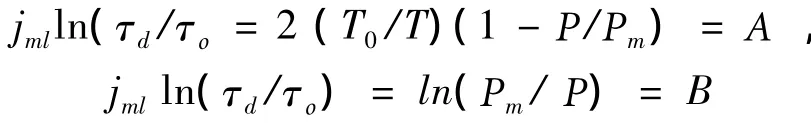
Attitude T/Toof ordinary ice(ice－1)，the existing temperature rangeis 251～273 K，changeing from 0.92 to 1.00.Dependence of A and B from P/Pmwhen T/To=0.96 are presented in Fig.2.Thick line shows the dependence of real(minimum of A and B) the relative durability(in logarithmic scale)from relative pressure，regardless of the mechanism of destruction.

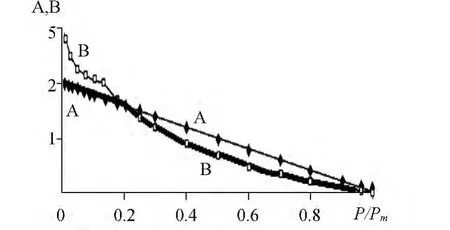
Fig.2 The dependence of A and B from P/Pm

The figure shows，that when P/Pm≥0.2 durability fragile body more(A＞B).This means，that the critical deformation jlachieved earlier than the body is falling apart.Consequently，to ensure the sustainability of buildings on such soils durability you expect from the formula(1)，as for plastic body.If P/Pm＜0.2， on the contrary，more“plastic”longevity(B ＞A)，so the body is falling apart before achieved critical deformation jl，as to the fragile body.Consequently，durability must be determined by formula(2)，as for the fragile body.

Power condition predominant work fragile or plastic fracture mechanism:P/Pm=0.2 at the substitution in him Pm=t/b，according to the formula(3)，easily converted to temperature:

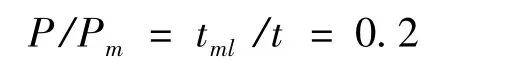
As follows from formulas(1)and(4)，at small loads or low temperatures“plastic”durability theoretically rushes to infinity.Actually in all cases，even if P = 0(at atmospheric pressure)，actual durability (bold line in Fig.1)is the end value.Formula(4)is suitable for all types of loads.

In Table 2［5］the experimental values are given relative strength of sandy soil(t= －10℃)jP=P/ P1(P1-quasi-instantaneous strength at τ1=1 min)，for various values of relative durability jτ=τ/τ1compressive jP1，stretching jP2and a shift to the jP3.Here are given the values jP4，calculated by the formula(4) when jml=0.11.Table 1 demonstrates a good agreement between the experimental data with calculations by the formula(4).Under all kinds of loads is thus almost the same jP(last column in Table 2).This summary of results(normalization unit)allows you to significantly reduce the amount of expensive experimental works.

Table 2 The dependence of the relative strength of sandy soil at compression jP1，stretching jP2and a shift to the jP3 from its relative longevity jτ，jP4-calculation when jl=0.11

2 Durability at variable pressure and temperature

The laws and constants of the destruction of frozen soil，primarily jl≈0.08÷0.12and Pm≈Lfidentified from the experiments with constant temperature and pressure are valid and when their variable values.

Let us illustrate this by example loads，changing with constant speed vp.For infinitesimal durability and dependence P or t from τ，it is permissible to substitute these values in(4)as a function of τ.In our case P=vp·τ，then

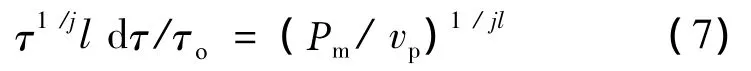
After integration(5)in the range of up τoto τ and simple transformation received expressions of dependence of durability and strength from loading rate jl:

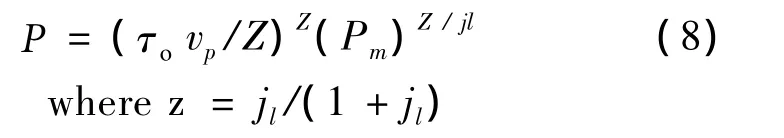
Extensive experimental study of the velocity dependence of the strength of frozen soils held A.G.Deryugin［6］.The results are shown in Fig.3.

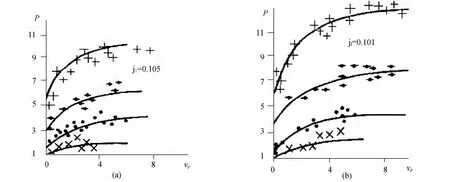
Fig.3 Dependence P(MPa)from vp(MPa/sec)in sandy loam-a and loam-b with a temperatures(℃，top to bottom):－15，－8，－4 and－2

Solid lines on the graphs-calculation by formula (6)，badges-resistance uniaxial compression at different temperatures.The graphs show a good agreement between the experimental and theoretical results.The analysis showed that the type of approximation dependences P from vtsignificantly easier(is linearized)，if to take into account the logarithms of these indicators Fig.4)

Methods of calculation of strength of frozen soils with variable load or temperature are of great practical value.They can significantly reduce the duration of the trials of frozen soils strength.Tests at constant load，or at a constant temperature continues to several months.A particularly large effect is reached at simultaneous increase of the load and temperature(in the range of negative values).The obtained integral equations strength at temperatures and loads growing with constant speed vpand vt

Fig.4 Dependence P/MPa from vp/MPa/sec in sandy loam(upper graph)and loam(lower)at the temperature/℃:1)－15 and 2)－2

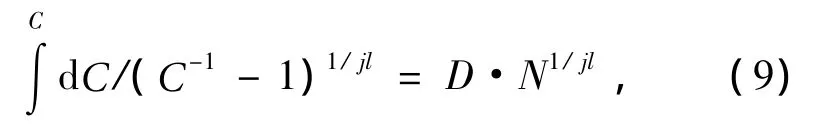
where C=vtτ/ti，D=vtτo/ti，N=vt/vpb-dimensionless variables;ti-initial temperature.

Calculations have shown，that the formula(9) with an error of about 3%can be simplified its left part of the form:exp［0.43Z/jl－2.3］;then we obtain the explicit expression for the jl:

where the parameter Z，dependent on C，is determined by the diagram in Fig.5.

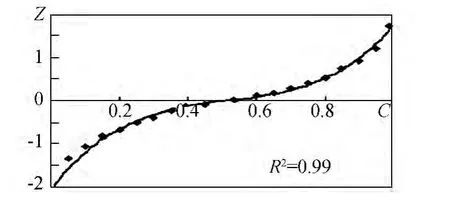
Fig.5 The dependence of Z on C

or its approximation:

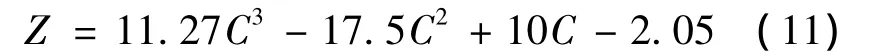
Developed an economical way to test the frozen soil for long-term strength using the formulas(9)～ (11).Time on the test does not exceed 10 minutes.Table 2 shows some examples of calculation of jltest results frozen pulverescent sand on the proposed technique.

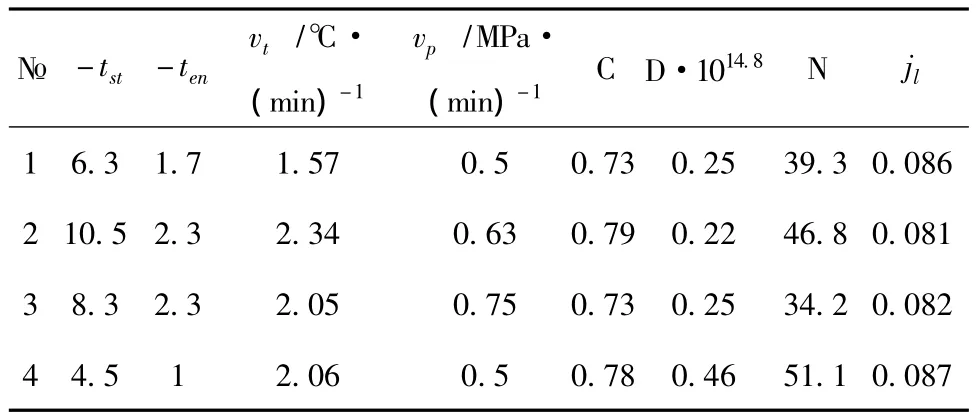
Table 3 Initial data and parameters in experiments(tst and ten-start and end temperature experiments)by definition jl

As the table shows，the value of jlat all velocities of the change t and P remains constant，close to the relative deformation melting jml≈0.083.

3 Conclusions

If the pressure on the frozen ground is about five times less equilibrium pressure at this temperature or the temperature in the same times below the melting temperature，the brittle fracture occurs earlier plastic; at higher pressures or temperatures destruction develops plastic scenario.In the first case，the process of destruction is described by the formula(2)，in the second－formulas(1)or(4).

Laws and constants destruction of frozen soil，primarily jl≈0.08÷0.12and Pm≈Lml，identified as a result of experiments with constant temperature and pressure，manifest and when you change these settings，

Test duration of frozen soil strength is significantly reduced in conditions of gradual increase in temperature and mechanical loading on the soil.

［1］ Konovalov A A.About the strength of the body when the temperature is near its melting point［J］.Engineering-physical Journal，2009，82(5):992-998.

［2］ Konovalov A A.General patterns of development ecogeosystem (deformation model)［M］.Saarbrucken:Palmarium academic publishing，2012.

［3］ Konovalov A A.Phase equilibrium and long-term strength of frozen soil［J］.Earth Cryosphere，2007，11(3):51-62.

［4］ Regel W R，Slutsker A I，Tomashevsky E E.Kinetic nature of strength of solid body［M］.Nauka:Handbook，Chemistry，1974，3:1 969-1 973.

［5］ Wyalov S S.Rheology of the frozen soil［M］.Stroiizdat，2000.

［6］ Deryagin A G.Study of the velocity dependence of the strength of frozen soils［J］.In:Engineering studies frozen ground，Novosibirsk:Nauka，1981:53-79.