木浆纤维素氨基甲酸酯的溶解及溶液流变性能研究
2014-03-19王乐军吴海燕尹翠玉
王 旭,王乐军,吴海燕,尹翠玉*
(1.天津工业大学改性及功能纤维天津市重点实验室,天津300160;2.山东海龙股份有限公司,山东潍坊261000)
纤维素是地球上丰富的可再生自然资源,具有广泛的用途,可用来制备再生纤维素纤维、纤维素薄膜、无纺布等。但纤维素很难溶于常规的溶剂,也很难用常规的方法进行加工,其利用率非常低[1]。因此,通过开发纤维素衍生物,实现了纤维素的再生和功能化,这引起了国内外研究者的广泛重视。纤维素氨基甲酸酯是纤维素浆粕和尿素在加热的条件下制备而成的,可以作为粘胶工艺中纤维素磺酸酯最有潜力的替代产品,因此一直成为了人们研究的热点[2]。纤维素氨基甲酸酯作为新型再生纤维素纤维的中间产品,可以很好地溶解在氢氧化钠(NaOH)溶液中,该溶液不仅可直接纺丝或按粘胶工艺制备再生纤维素纤维,也可以与粘胶混合纺丝,这为落后粘胶厂技术改造、适应新时期发展要求提供了一条新的路径[3-4]。纤维素氨基甲酸酯的溶解过程是其加工与应用的一个重要工序。溶解效果与溶液流变性能不仅影响到纺丝原液的稳定性和加工性能,还间接影响到成品的质量。目前国内对纤维素氨基甲酸酯的溶解及溶液的流变性能研究较多[5-6],但研究中采用的原料主要为棉浆纤维素氨基甲酸酯,有关木浆纤维素氨基甲酸酯(CC)在NaOH溶液中的溶解及流变性能研究未见报道。作者以CC为原料,对CC的溶解及溶液的流变性能进行了研究,为CC的加工应用提供依据。
1 实验
1.1 原料与仪器
CC:由木浆粕制得,聚合度350,CC中含氮量分别为1.2%,3.4%,4.4%,实验室自制。NaOH溶液:质量分数为9%,实验室配制。
BX-51型热台偏光显微镜:日本奥林巴斯株式会社制;RVDV-II+可编程控制式旋转黏度计:扭矩为0~718.7 mN·m,美国Brookfield公司制。
1.2 实验方法
在小烧杯中加入一定量的 CC和9%的NaOH溶液,强力搅拌器搅拌20 min,然后降温至-10℃以下,溶解20 min,室温下搅拌20 min,最后将溶液离心脱除气泡,得到质量分数为3%~9%的CC溶液,见表1。
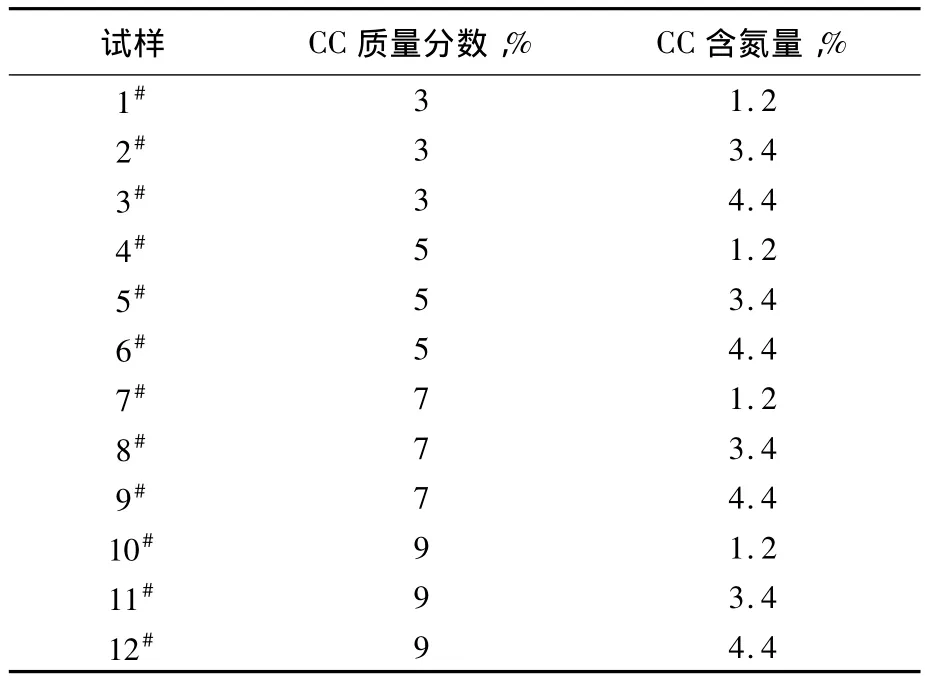
表1 配制的CC溶液试样Tab.1 Prepared CC solution samples
2 结果与讨论
2.1 CC含氮量对溶解的影响
从图1可看出,7#试样中有大量未溶解的CC,9#试样中没有未溶解的CC。这说明含氮量越高越有利于CC的溶解。这是由于CC含氮量越高,其酯化程度越高,链间距离越大,有利于溶剂渗透到纤维素内部,从而表现为较好的溶解性。

图1 不同含氮量的CC溶液的偏光显微镜照片Fig.1 Polarizingmicroscope images of CC solutionswith different nitrogen content
2.2 CC浓度对溶解的影响
从图2可以看到,CC质量分数从3%增加到7%后,可以观察到溶液中有大量未溶解的纤维素片段,且片段多呈现木浆纤维素及禾本类纤维素溶胀时所独有的念珠状结构,并且出现了不透明的半凝胶体。这一现象表明,CC酯化度低,少量的甲酸酯基团所产生的溶剂化作用不足以使CC完全溶解于NaOH溶液。

图2 不同浓度的CC溶液的偏光显微镜照片Fig.2 Polarizingmicroscope images of CC solutionswith different concentration
2.3 CC含氮量对溶液流变性能的影响
从图3可以看出,不同 CC含氮量的 CC/ NaOH溶液的σ均随γ的增加而增加,且呈现非牛顿流动,均属于非牛顿流体。其中,8#与9#试样的流变曲线非常接近,二者延长线与纵坐标轴相交所得截距很小,因此可以判断8#,9#溶液基本不存在剪切屈服应力,属于假塑性流体。
虽然7#与8#,9#溶液组分相同,但相同γ下其σ更大,流变曲线延长线与纵坐标轴相交所得截距较8#,9#相比要大得多,从而说明7#溶液存在一个较大剪切屈服应力,具有明显的Bingham流体特征。这一结果也证明,含氮量低的CC在NaOH溶液中的溶解效果不好,未完全溶解的纤维素在溶液中溶胀并交联,形成半凝胶状溶液。
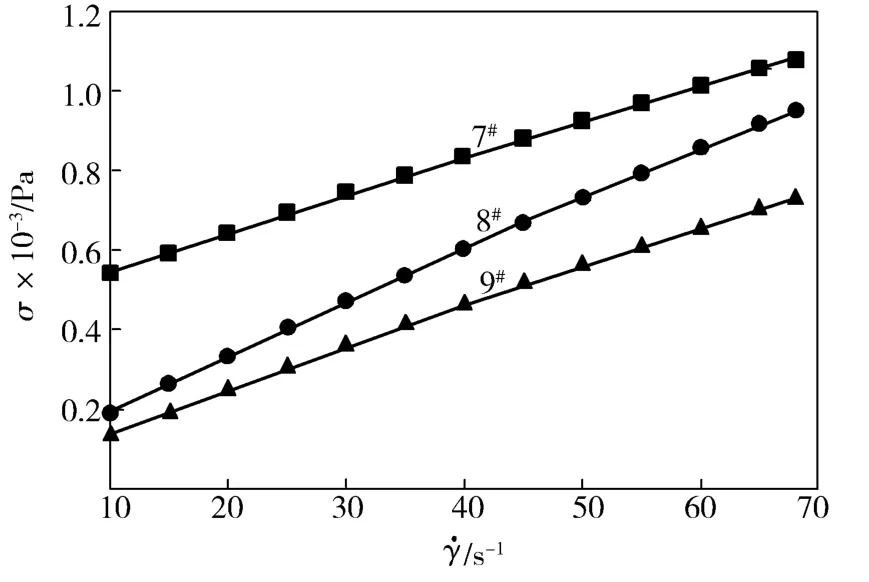
图3 不同含氮量的CC溶液的流动曲线Fig.3 Flow curves of CC solutionswith different nitrogen content
从图4可以看出,3种溶液的ηa均随γ的升高而下降,都属于切力变稀流体。8#与9#因原料含氮量接近,二者ηa-γ曲线非常近似,而含氮量较低的7#与二者之间存在明显差异。7#溶液的ηa随γ的变化幅度明显要大于8#与9#。这一现象说明由于含氮量低的CC酯化度低,所以7#溶液中低相对分子质量部分含量较多,在剪切流动中取向的低相对分子质量分子对溶液起到了润滑增塑的作用,致使溶液对γ的变化较为明显,ηa下降更为显著;另一方面,ηa变化过快也说明了含氮量较低的CC的相对分子质量分布要比含氮量高的CC的宽,对γ的变化更为敏感[7]。

图4 不同含氮量的CC溶液的ηa-γ关系曲线Fig.4 Curves ofηa-γfor CC solutionswith different nitrogen content
非牛顿指数(n)是表征流体偏离牛顿流体程度的参数,结构黏度指数(△η)表征聚合物溶液的结构化程度。从表2可以看出,CC浓度相同的溶液的n随含氮量的升高而增大,△η随含氮量的升高而减小。显然,3种溶液中含氮量为4.4%的CC溶液流动性能最好,含氮量为1.2%的CC溶液偏离牛顿流体的程度最大,不但其流动性相对较差,其△η也比其他2种溶液大许多,可纺性不佳。

表2 不同含氮量的CC溶液的n和△ηTab.2 n and△ηof CC solutionswith different nitrogen content
2.4 CC浓度对溶液流变性能的影响
从图5可看出,在CC含氮量为4.4%时,不同浓度的CC溶液均没有表现出明显的剪切屈服应力,都属于假塑性非牛顿流体。这说明当CC达到理想含氮量时,即使高浓度的CC/NaOH溶液也能表现出较好的流变性能。

图5 不同浓度的CC溶液流动曲线Fig.5 Flow curves of CC solutionswith different concentration
从图6可看出,当CC含氮量为4.4%时,不同浓度的CC溶液ηa均随γ的升高而下降,属于切力变稀流体。从表3可看出:CC溶液的n随溶液浓度的增加而减小,溶液的流动更加偏离牛顿流动,说明溶液的不稳定性增加[8],只有在浓度较小时接近牛顿流体;而△η随着浓度的增大而增大,这是由于大分子的流动使分子链沿流动方向发生转移,随着浓度的增加,单位体积内所含分子和分子链段数目增多,分子间相互作用增强,分子链间的缠结点也增多,进而引起流动单元变大,运动阻力也增大,导致溶液的结构化程度变大;不同浓度的CC溶液的△η增长幅度较小,质量分数9%的CC溶液在满足纺丝工艺黏度要求的同时,其△η仍能保持在一个理想的范围,因此,含氮量为4.4%的CC溶液具有较好的可纺性。

图6 不同浓度的CC溶液ηa-γ关系曲线Fig.6 Curves ofηa-γfor CC solutions with different concentration
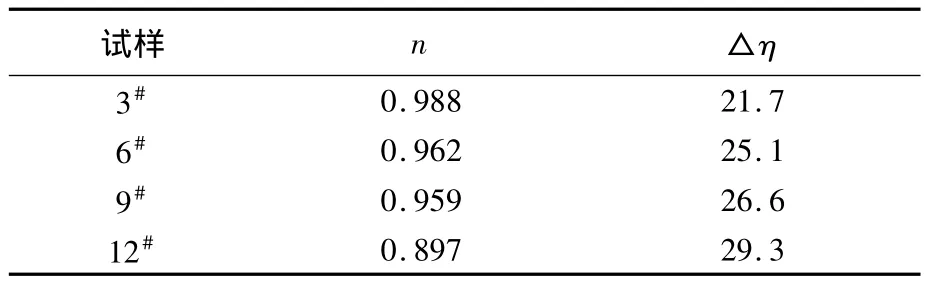
表3 不同浓度的CC溶液的的n和△ηTab.3 n and△ηof CC solutions w ith different concentration
从图7可知,随着CC溶液浓度的增加,溶液的ηa增加,曲线呈现指数关系增加,符合Flory方程[9]。这是由于随着高聚物浓度的增加,缠结点的密度增加,所以CC溶液的ηa对浓度具有很强的依赖性。采用幂次公式拟合CC溶液ηa与浓度的关系见式(1)。

式中:wcc为CC浓度。
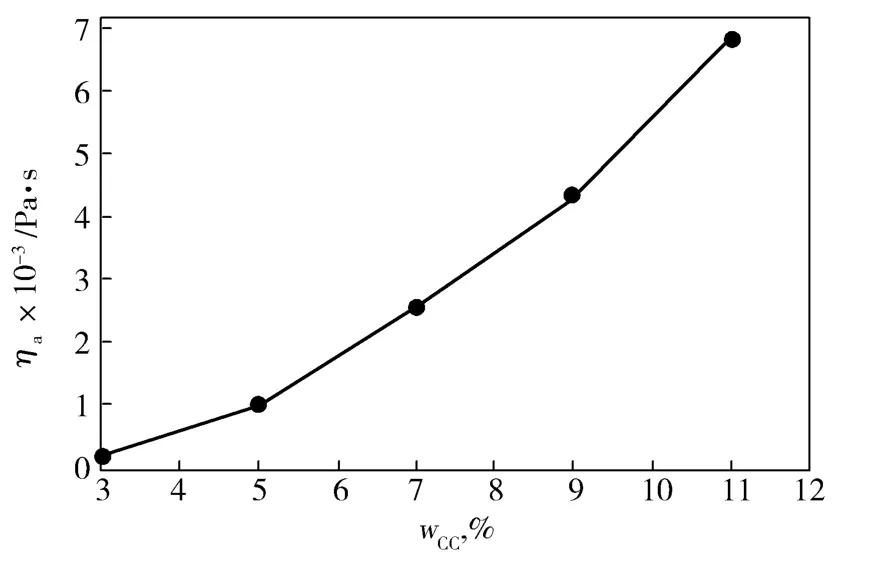
图7 CC溶液ηa随w CC的变化Fig.7 Curves ofηa versus w CC of CC solution γ为10 s-1。
3 结论
a.含氮量高的CC在NaOH中的溶解情况要明显优于含氮量低的CC,能够获得较高浓度的CC溶液。
b.CC溶液属于假塑性非牛顿流体,含氮量低的CC所得溶液因溶解不充分而存在剪切屈服应力,具有明显的Bingham流体特征,呈现木浆纤维素及禾本类纤维素溶胀时所独有的念珠状结构。
c.CC溶液均具有切力变稀性,较高含氮量的CC可纺性也较好。
d..随着CC溶液浓度的增加,溶液的ηa增加,符合Flory方程。
[1] Fink H P,Weigel P,Purz H J,et al.Structure formation ofregenerated cellulosematerials from NMMO-solutions[J].Prog Polym Sci,2001,26(9):1473-1524.
[2] 程博闻,任元林,康卫民.氨基甲酸酯法纺制阻燃纤维素纤维[J].纺织学报,2007,28(4):19-21.
[3] 何春菊,王庆瑞.纤维素纤维的生产新方法[J].中国纺织大学学报,1998,24(4):110-113.
[4] Orbanowski A.Barbara.Preparation of cellulose carbamate,its properties and applications[J].Polymer,1990,5(7/8): 233-236.
[5] 哈丽丹·买买提,吾满江·艾力.纤维素氨基甲酸酯溶液的流变性能[J].纺织学报,2009,30(1):1-4.
[6] 尹翠玉,张建丽,沈新元.纤维素氨基甲酸酯溶液的流变性能[J].合成纤维工业,2005,28(6):28-30.
[7] 徐佩弦.高聚物流变学及其应用[M].北京,化学工业出版社,2003:120-135.
[8] 臧昆,臧己.纺丝流变学基础[M].北京,纺织工业出版社,1993:57-85.
[9] 柴志宽.Flory状态方程理论与聚合物混合物的热力学[J].Acta Polym Sin,1985,1(4):299-305.
