BP-AdaBoost模型在光纤陀螺零偏温度补偿中的应用
2014-03-19刘元元杨功流李思宜
刘元元 杨功流 李思宜
(北京航空航天大学 仪器科学与光电工程学院,北京 100191)
光纤陀螺具有可靠性高、寿命长、启动时间短、动态范围大等优点,已经成为新一代惯性制导、测量系统中的主要器件.构成光纤陀螺的核心部件对温度较为敏感,当环境温度发生变化时,在陀螺的输出信号中将产生非互易性相位误差,导致光纤陀螺零位漂移不稳定,严重制约着光纤陀螺的精度,因此有必要采取温度控制或温度补偿措施来消除这种误差[1].研究表明,温度变化引起的误差难以用明确的函数关系表示,采用非线性模型对光纤陀螺的零偏进行建模,从而实现对漂移的预测,受到了人们越来越多的关注.
人工神经网络处理非线性问题具有很强的优越性,尤其是前向网络[2-3]在函数逼近、系统辨识和优化等方面应用很广.考虑影响光纤陀螺温度漂移的各种因素,文献[4-7]建立了神经网络模型对其进行辨识.如何最优地构造和训练一个神经网络,保证网络的泛化能力,更多地取决于使用者的经验和不断地试凑.
鉴于文献[8-10],运用 AdaBoost(Adaptive Boosting)算法提升单个BP(Back Propagation)神经网络预测能力,克服实验模型和数据的不确定性影响.本文提出了基于AdaBoost算法与BP神经网络集成的预测模型,在大量的光纤陀螺输出实验数据的基础上,进行了零偏的建模与补偿,验证了该模型的有效性.
1 温度漂移的误差补偿方法
1.1 光纤陀螺温度误差机理分析
温度对光纤陀螺的影响包括噪声和漂移两个方面.文献[11]推导出了两束干涉光分别沿着顺时针和逆时针方向传输时,光纤环温度变化产生的热致非互易相位延迟为
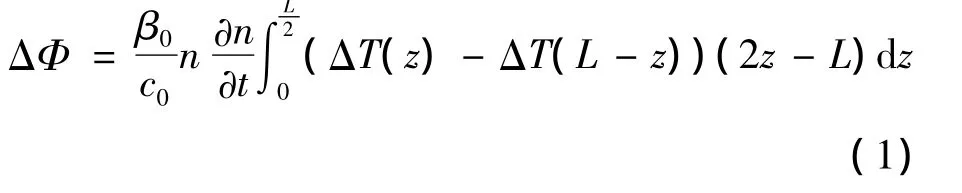
式中,β0=2π/λ0为光在真空中的传输常数;c0为光在波导中的光速;ΔT(z)为光纤z点温度分布的变化量;L为光纤总长度;n为光纤折射率.通过式(1)的分析可以看出:非互易性误差的大小除了与环境温度的分布及其变化有关,还与光纤敏感环的参数及绕制方法有关,因此补偿光纤陀螺温度漂移误差的方法主要包括光纤陀螺结构及组成部件的改进、光纤环绕制技术的改善、光纤陀螺温度控制和误差建模及补偿等4个方面.
1.2 温度漂移建模与补偿
温度对光纤陀螺零偏的影响主要表现在温度变化、温度梯度和温变速率3个方面.工程上常用的方法[1]是将光纤陀螺的零偏随温度的变化近似为线性关系,建立零偏的多项式模型、自回归(AR,Autoregressive)模型、自回归滑动平均(ARMA,Autoregressive Moving Average)模型等,其中多项式模型简单易行,应用最为广泛.实际上,光纤陀螺的零偏温度特性具有复杂的非线性特点,BP神经网络因其具有良好的逼近复杂非线性函数的能力,在光纤陀螺的温度漂移模型与补偿中受到了重视.文献[12]证明通过训练多个神经网络并将其集成输出,会显著提高神经网络的泛化能力.
本文运用AdaBoost算法的思想集成多个BP神经网络的输出.将每一个BP神经网络作为弱预测器,反复训练每一个BP神经网络,最终得到多个BP神经网络集成的强预测器.
2 BP-AdaBoost预测模型
2.1 BP 神经网络
BP神经网络[3]本质上是一种输入到输出的映射,只要用已知的模式对网络进行训练,网络就会具有输入到输出之间精确的映射关系,特点是信号前向传播,误差反向传播.根据映射网络存在定理(Kolmogorov定理):1个3层前向网络能在任意期望的精度上逼近任意的连续函数.本文使用3层的神经网络,结构见图1.

图1 3层BP神经网络结构
2.2 AdaBoost算法
通过一个构造性方法对“一个弱学习器能否被提升为一个具有任意精度的强学习算法”,Schapire作了肯定回答.文献[13-14]提出通过调整权值而运作的 AdaBoost,AdaBoost.M1,Ada-Boost.M2,AdaBoost.R 算法,解决了早期 Boosting算法很多实践上的问题.至此,AdaBoost算法应运而生.
AdaBoost是Boosting家族的代表算法,该模型假设存在弱学习算法,这些算法获得的分类器的预测能力只比随机预测好一点点.AdaBoost通过推进这些弱学习算法从而获得任意高精度的分类器.AdaBoost算法不要求事先知道弱学习算法预测精度的下限而非常适用于实际问题.Ada-Boost算法描述如下.
给定学习样本:

给定样本初始权重:

给定迭代次数 T,当 t=1,2,…,T 时
1)利用样本权重Wt训练弱学习器
2)获取弱学习器的预测函数ht:x→y,满足的样本,计算
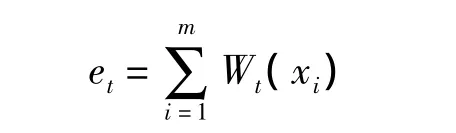
4)更新样本权重
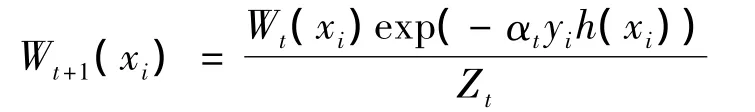
输出最终预测函数:
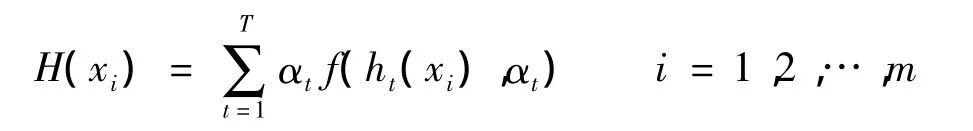
其中,Zt为归一化因子,目的是保证权重比例不变的情况下使分布权值和为1.AdaBoost算法与BP神经网络的集成学习模型,见图2.
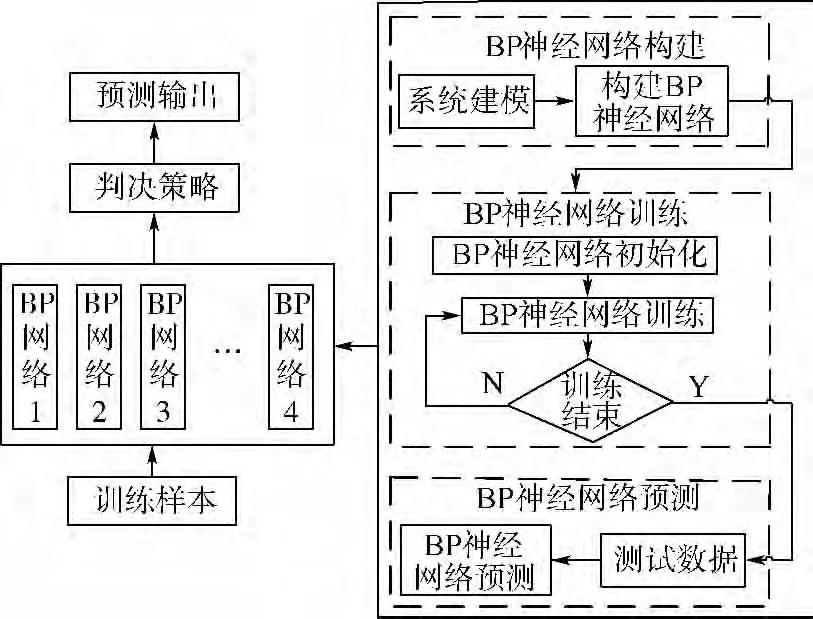
图2 BP-AdaBoost预测模型示意图
3 BP-AdaBoost模型建立及分析
3.1 BP神经网络结构以及网络参数确定
光纤陀螺内部安装有Pt800温度传感器,壳内温度是唯一的实际观测量.建立以温度、温度梯度、温度与温度梯度的乘积项为输入,陀螺零偏为输出的BP神经网络.隐含层节点的数目理论上越多,网络输出精度越高.然而节点越多,计算量越大,BP神经元输入区域重叠性也随之增大,导致所有神经元的输出均为1,无法产生不同的响应曲线,精度反而下降.为了确定隐含层神经元的数目,选取程序运行10次得到决定系数的平均值为评价指标[15].决定系数 R2的计算如式(2),范围为[0,1],愈接近1,表明模型的性能愈好.从表1可以看出,当神经元个数为50时,决定系数平均值最大.

其中,l为样本的数目;yi为陀螺真实的输出数据;^yi为模型预测的数据.

表1 BP神经网络运行10次的具体结果
3.2 确定AdaBoost算法的迭代次数L
通过观测迭代中测试样本的误差变化来确定最佳的L值,在AdaBoost算法中,迭代次数在1~35之间变化,每个L值运行5次,取5次运行误差的平均值作为最终的强预测器误差的评价指标,如图3所示.选择最小的平均测试误差对应的迭代次数为BP-AdaBoost模型的迭代常值,避免出现过学习.从图3可以看出,预测误差的减小随着迭代次数的增加变得缓慢,甚至出现不稳定的现象,本文中,取迭代次数为30.
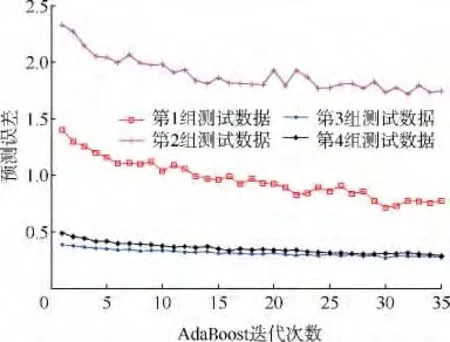
图3 BP-AdaBoost模型迭代次数与预测误差的变化曲线
4 实验设计及结果分析
4.1 实验设计
本次实验以某型惯性组件的光纤陀螺为研究对象,将陀螺组合固定在水平带有温控箱的位置转台上.采集4组不同温度范围以及温变速率下的陀螺输出数据,见图4、图5.
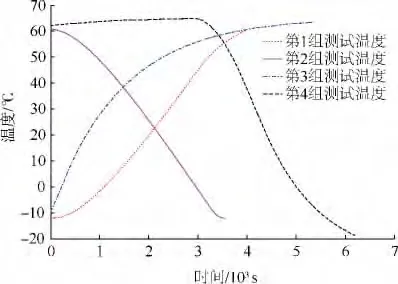
图4 4组数据的温度变化曲线
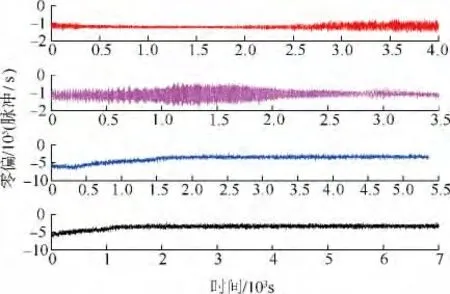
图5 4组陀螺输出数据
4.2 实验结果分析
采集光纤陀螺4组数据,分别建立线性回归模型、混合线性回归模型[16]、BP神经网络模型、BP-AdaBoost模型对其进行补偿.BP神经网络隐含层节点数为50,隐含层神经元传递函数采用tansig函数,输出层采用purelin函数,训练步数定为30步,学习系数定为0.01.AdaBoost的迭代次数选为30.弱预测器的训练样本从每组数据中按照10∶1比例随机选取,预测样本为陀螺的整组输出数据.选择其中1组具有代表性的输出数据,对比4种补偿模型,如图6~图9所示.从补偿结果可以看出,BP-AdaBoost模型对光纤陀螺的零偏补偿效果显著,所获得的零偏稳定性如表2所示.图10对比了强、弱预测器的预测误差,图11显示了BPAdaBoost算法每次迭代的难训练样本的数目,随着迭代次数的增大,训练样本的难度越来越大.

图6 线性回归补偿前后数据曲线

图7 混合线性回归补偿前后数据曲线
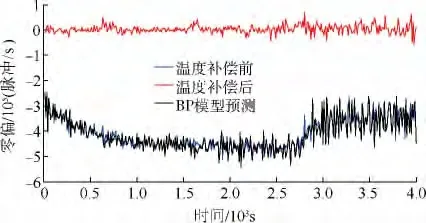
图8 BP神经网络补偿前后数据曲线
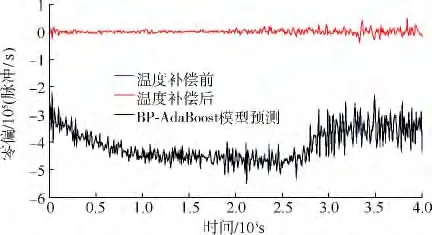
图9 BP-AdaBoost补偿前后数据曲线
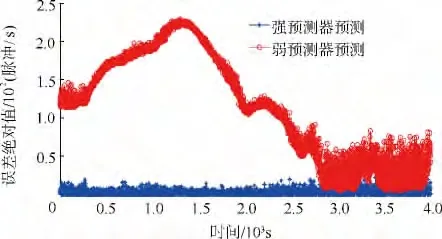
图10 强弱预测器预测误差的对比

图11 迭代次数与训练数据样本曲线

表2 陀螺补偿前后零偏稳定性对比 (°)/h
5 结论
本文用BP-AdaBoost模型对光纤陀螺的输出数据进行了预测,对光纤陀螺的零偏进行了补偿.与线性回归模型、混合线性回归模型、BP神经网络做了对比分析:①混合线性回归模型,预测的结果优于只考虑温度影响的线性回归模型,说明光纤陀螺的零偏具有自回归特性;②BP模型,预测的结果部分优于线性回归及混合线性回归模型,说明光纤陀螺的零偏温度特性具有复杂非线性的特点且BP模型存在泛化能力差的缺点;③BPAdaBoost模型,提升单个BP神经网络的预测结果,提高了BP神经网络的泛化能力.进一步改善了光纤陀螺的零偏稳定性,对光纤陀螺在导航中高精度的保持,具有重要的理论指导意义.在本文研究的基础上,可采用多个不同结构的弱预测器补偿光纤陀螺的零偏温度误差.
References)
[1]韩冰,林玉荣,邓正隆.光纤陀螺温度漂移误差的建模与补偿综述[J].中国惯性技术学报,2009,17(2):218 -224 Han Bing,Lin Yurong,Deng Zhenglong.Overview on modeling and compensation of FOG temperature drift[J].Journal of Chinese Inertial Technology,2009,17(2):218 -224(in Chinese)
[2] Xiao Zhi,Ye Shijie,Zhong Bo,et al.BP neural network with rough set for short term load forecasting[J].Expert Systems with Applications,2009,36(1):273 - 279
[3]韩力群.人工神经网络理论:设计及应用[M].北京:化学工业出版社,2002 Han Liqun.Theoretics,design and application of artificial neutral network[M].Beijing:Chemical Industry Press,2002(in Chinese)
[4]申冲,陈熙源.基于提升小波与灰色神经网络的光纤陀螺振动误差建模[J].中国惯性技术学报,2011,19(5):611 -614 Shen Chong,Chen Xiyuan.Vibration error modeling of FOG based on lifting wavelet and grey neural network[J].Journal of Chinese Inertial Technology,2011,19(5):611 - 614(in Chinese)
[5]周琪,秦永元,成研,等.光纤陀螺热致漂移误差的模糊补偿[J].中国惯性技术学报,2010,18(4):471 -475 Zhou Qi,Qin Yongyuan,Cheng Yan,et al.Fuzzy compensation of thermally induced bias drift in fiber optical gyro[J].Journal of Chinese Inertial Technology,2010,18(4):471 - 475(in Chinese)
[6]冯丽爽,南书志,金靖.光纤陀螺温度建模及补偿技术研究[J].宇航学报,2006,27(5):939 -942 Feng Lishuang,Nan Shuzhi,Jin Jing.Research on modeling and compensation technology for temperature errors of FOG[J].Journal of Astronautics,2006,27(5):939 -942(in Chinese)
[7] Chen Xiyuan.Modeling temperature drift of FOG by improved BP algorithm and by Gauss-Newton algorithm[M].Berlin:Springer,2004:805 -812
[8] Schapire R E.The boosting approach to machine learning:an overview[J].Nonlinear Estimation and Classification,2003:149-172
[9] Green M,Ekelund U,Edenbrandt L,et al.Exploring new possibilities for case-based explanation of artificial neural network ensembles[J].Neural Networks,2009,22(1):75 -81
[10] Qiao Changming,Sun Shuli,Hou Ying.Design of strong classifier based on adaboost M2 and back propagation network[J].Journal of Computational and Theoretical Nanoscience,2013,10(12):2836-2840
[11] Shupe D M.Thermally induced nonreciprocity in the fiber-optic interferometer[J].Applied Optics,1980,19(5):654 -655
[12] Hansen L K,Salamon P.Neural network ensembles[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(10):993 -1001
[13] Freund Y,Schapire R E,Abe N.A short introduction to boosting[J].Journal of Japanese Society for Artificial Intelligence,1999,14(5):771 -780
[14] Islam M,Yao Xin,Murase K.A constructive algorithm for training cooperative neural network ensembles[J].IEEE Transactions on Neural Networks,2003,14(4):820 -834
[15]史峰,王辉,郁磊,等.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2012:237-247 Shi Feng,Wang Hui,Yu Lei,et al.Analysis of MATLAB intelligent algorithm in 30 cases[M].Beijing:Beihang University Press,2012:237 -247(in Chinese)
[16]陈维娜,曾庆化,李荣冰,等.微机械陀螺温度混合线性回归补偿方法[J].中国惯性技术学报,2012,20(1):99-103 Chen Weina,Zeng Qinghua,Li Rongbing,et al.Mixed linear regression temperature compensation method for annular-vibrating MEMS gyroscope[J].Journal of Chinese Inertial Technology,2012,20(1):99 -103(in Chinese)
