带静态参数的高超声速飞行器轨迹优化算法

张红文

(北京航空航天大学 宇航学院，北京 100191)

张科南

(北京机电工程研究所，北京 100074)

陈万春

(北京航空航天大学 宇航学院，北京 100191)

飞行器轨迹优化问题本质上是一个最优控制问题.通常的轨迹优化问题是一个动态优化过程.通过对动态参数(如控制变量、状态变量等)的寻优，获得满足极值条件的解.随着工程设计系统化的加强、复杂性的增加，单纯的动态优化越来越不能满足总体设计的要求，有许多静态参数也需要随着动态参数的优化而优化，以获得全局最优的轨迹.在动态优化中，所有不随时间变化的参数均可作为优化变量进行优化.例如动态优化中的初始参数、终端参数、飞行时间和过程约束量等，以及与轨迹密切相关的飞行器总体参数或者叫设计变量，如起飞重量、推进系统设计参数和气动外形特性参数等［1］.本文称这一类问题为带静态参数的轨迹优化问题.

关于动态轨迹优化问题的研究，学者们已经取得了丰富的研究成果.尤其是在直接法领域，计算机技术的飞速发展为直接法的应用提供了有利条件.

Gauss伪谱法［2－3］是近年来比较热门的一种正交配点算法.其收敛速度快，鲁棒性好，并且能够得到间接法才能获得的协态变量信息.对于带静态参数的轨迹优化问题，只有为数不多的几篇文献可供参考.文献［4］提出了静态动态混杂优化方法，将静态参数看作导数为零的状态变量，推导出了广义的一阶必要条件，但是没有给出算例，也没有提供两点边值问题(TPBVP，Two-Point Boundary Value Problem)的数值求解方法.Hull在其著作中对最优控制中的静态参数进行了研究［5］，同样将这些静态参数加入原系统中，构成增广系统，通过求变分，给出了最优一阶和二阶条件.Hull提供了几个简单算例，将终端时间作为静态参数进行处理，得到了解析解，但也没有给出TPBVP的数值算法.

本文在文献［4－5］的基础上，总结并给出了静态参数是飞行时间，初始、终端状态参数，以及设计变量几种情况下的最优一阶条件.同时利用Gauss伪谱法提供的协态变量信息，提出了求解TPBVP的一种新算法.该算法结合了直接法和间接法的优点，具有收敛速度快，计算精度高的优点，完成一条实际飞行时间2 000 s的轨迹优化计算只需要数秒钟时间.最后，以乘波体为研究对象，给出了一个气动外形/轨迹一体化优化设计算例，验证了本文方法的有效性.

1 最优控制问题描述

1.1 一般最优控制问题描述

最常见的是固定起点、终端时间未定的最优控制问题，即Bolza问题，设系统状态方程为

式中，状态变量x(t)∈Rn;控制变量u(t)∈Rm，目标函数为

终端状态变量需满足约束:

求解上述问题时，引入拉格朗日乘子λ(t)和ν，构造增广目标函数如下:

定义哈密顿函数:

增广终端约束函数:

状态方程:

协态方程:

控制方程:

边界条件:

式(7)～式(13)构成了一般最优控制问题的一阶优化必要条件.

1.2 带静态参数的最优控制问题

按照在轨迹优化过程中应用，将静态参数分为3类:终端时间、起始或终端状态变量和设计变量.

1.2.1 静态参数为终端时间

为了方便两点边值问题求解，需要将自由终端时间问题转换为固定终端时间问题，引入无量纲时间变量τ:

于是1.1节的最优控制问题中，目标函数式变形为

对应的一阶必要条件状态方程式、协态方程式分别变形为

其余条件不变.此时，终端时间成为了优化过程中的一个未知静态变量，式(13)是用来求解未知终端时间的方程.

1.2.2 静态参数为边界点状态变量

考虑更一般的情况，初始时间和初始状态不再固定，假设初始条件约束为

引入拉格朗日乘子ξ，将终端约束式增广为端点约束:

得到新的增广目标函数为

同样对该目标函数取变分后，得到新的一阶必要条件，其中状态方程、协态方程和控制方程形式未变，边界条件增加两个方程式:式(21)和式(22)，式(21)提供了未知初始状态变量的协态初值，式(22)用来求解未知的初始时间.

1.2.3 静态参数为设计变量

动态轨迹优化过程中，有时需要考虑一些设计变量的优化，例如飞行器起飞重量、气动外形几何参数等.

按照1.2.1节的方法，一般的自由终端时间问题均可以转换为固定终端时间问题，假设p表示优化过程中的设计变量，带设计参数的固定终端时间优化问题的目标函数可以表示如下:

引入方程:

则可以将设计参数p看作状态变量.由于p不随时间变化，p的两个端点值可以认为是自由的，这样，该问题可以看作是状态变量p初始值和终端值自由的最优控制问题.

式(23)改写为

其中，p=p0=pf.此时最优控制问题的一阶优化条件有如下改动.

状态方程扩维:

协态方程扩维:

控制方程形式不变，边界条件也需要进行扩维处理，添加关于p的两个方程:

其余边界条件与一般最优控制问题中相同.

2 最优控制问题求解

最优控制问题的一阶必要条件构成了一个两点边值问题.关于两点边值问题的求解，目前主要有打靶法、差分法和有限元法等几种算法［6］.不管采用哪种算法，都需要对两点边值问题的初值进行估计，如果估计不准确，则很难得到理想的解.这是求解两点边值问题的难点所在.因为最优控制问题中的协态变量没有明显的物理意义，协态变量初值估计一直以来都是一个研究难点.不过，近年来对伪谱法研究发现，这种新的直接法不但收敛速度快，而且满足协态映射定理，可以提供最优控制问题的协态信息.于是，本文提出一个求解两点边值问题的新思路:先用Gauss伪谱法进行求解，获得次优解，包括状态变量、协态变量.以次优解作为两点边值问题的初始参考，利用基于有限元法的边值问题求解器进行计算.

2.1 协态映射原理

根据Gauss伪谱方法转换后得到的非线性规划(NLP，Non-Linear Programming)问题的 KKT(Karush-Kuhn-Tucker)条件，跟原Bolza问题的连续一阶必要条件利用Gauss离散之后的形式是完全等效的［3］.

协态映射原理说明，求解Gauss伪谱转换后的NLP问题与求解利用Gauss伪谱方法离散的最优控制一阶必要条件是等价的.前者是直接方法，后者是间接方法.两者间的关系如图1所示.

图1 Gauss伪谱转换方法

理论上，只要设置足够多的Gauss点，Gauss伪谱方法转换后的NLP问题的解是满足最优一阶必要条件的.然而，在实际应用过程中，随着Gauss点的增多，优化变量越来越多，运算速度大幅度下降，而且对于像飞行器轨迹优化这类复杂的非线性优化问题，NLP求解器往往不容易收敛到最优解.故本文将Gauss伪谱方法作为最优解初值生成的手段，这样精度要求不高，可以利用比较少的Gauss点，快速获得次优解.

2.2 两点边值问题计算

为求解边值问题，Matlab软件提供了一个bvp4c的函数文件［7］.该文件是依据有限元法编写而成.解题的基本思路如下.

1)首先把待解问题转化为标准边值问题:

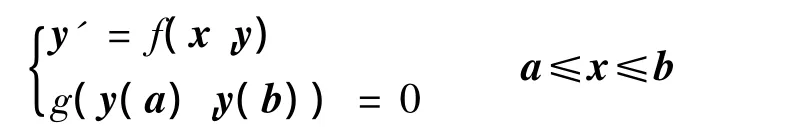
2)因为边值问题可以多解，所以需要一个初始猜测.该猜测网包括区间［a，b］内的一组网格点和网格点上的解S(x).

3)根据原微分方程构造残差函数:显然，当猜测解S(x)等于真解y(x)时，有残差r(x)=0，边值g(S(a)，S(b))=0.S(x)不是真解，残差不为零.

4)利用原微分方程和边界条件，借助迭代不断产生新的S(x)，使残差不断减小，从而获得满足精度要求的解.

整个求解过程中，第2)步初始猜测是很关键的.如果初始猜测离真解太远，则迭代求解无法进行.

根据Gauss伪谱方法解的特点，选择Gauss点作为初始猜测网格点，而对应的每个网格点上的状态变量和协态变量的值作为初始猜测网格点上的解，从而构成一个完整的初始猜测，并且该猜测十分接近最优解，能够保证迭代的顺利进行.

3 算例分析

以乘波体研究对象，将气动外形参数作为静态优化参数，优化求解全局最大航程问题.

3.1 乘波体简介

文献［8］提出了一种全新的高超声速飞行器布局，因为是由一种已知的超声速或高超声速流场生成的气动构型，在设计点成波体的整个前缘产生贴附的激波，整个构型像是骑在激波面上，所以被称为乘波体(waverider)，或称乘波构型，如图2所示.

图2 圆锥绕流场及锥导乘波体示意图

3.2 乘波体外形参数选择

锥导乘波体的外形设计是从给定最初的高超声速流场开始的，因此流场参数、激波形状和乘波体在流场中的位置都对乘波体的外形有直接的影响，如图2所示.

通过实验设计分析发现，对外形影响最大的参数主要有4 个:Macfg，βcfg，XL，ω.而这其中又属ω对形状的影响最明显，为降低间接法求解难度，本文中将问题进行简化，只研究ω的变化对外形的影响，固定其余3个参数.这样，外形优化参数就只有一个了，即ω.

3.3 气动系数计算

一旦外形确定以后，便可以进行气动系数的计算［9－10］.本文选用基于高速无粘流理论的气动工程计算方法——牛顿面元法［11］，进行气动估算.

间接法求解，需要得到气动系数的解析表达式.为此，首先利用牛顿面元法计算多种工况下乘波体气动力系数，然后利用响应面方法(RSM，Response Surface Method)［12］将离散的气动数据代理为解析多项式形式.

乘波体底部出口型线高宽比的变化范围为

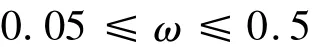
高宽比的变化将引起底部厚度以及整个乘波体长度的变化;其余3个外形参数固定，其中Macfg=10，βcfg=12°，XL= －19.5m.攻角变化范围－5°≤α≤20°，拟合以后得到的响应面多项式为

3.4 质量和参考面积计算

乘波体外形确定以后，其质量和参考面积可以通过估算公式获得.

总质量可以通过下式估算.

气动参考面积Sref取乘波体XY平面的投影面积.本文中外形参数只有高宽比一个，故可以将总质量和参考面积拟合为高宽比的函数:

3.5 动力学方程

只考虑乘波体在纵平面内的运动，动力学方程如下:

式中，r为飞行器质心到地心的距离;V为对地速度;γ为航迹角;θ为经度.

大气密度采用简化模型:

式中，ρ0为海平面大气密度;h为飞行器距当地海平面的高度，h=r－R0，R0为地球半径;常数H0=7200m.

3.6 间接法求解过程及结果

目标函数均为使航程最大化，假定飞行器只在纵平面内运动，可以表示为纵程最大化:

初始条件和终端条件如表1所示.

表1 乘波体外形/轨迹两层优化边界条件

优化过程中，将ω看作状态变量，故系统的状态方程除了式(35)～式(38)以外，还需添加一个的有效范围为0.05≤ω≤0.5.

对应地引入新的协态变量λω，哈密顿函数写为

增加一个协态方程:

控制表达式为

经过整理后有

另外，终端时间自由对应的横截条件:

最后，协态边界条件

该系统共有5个状态变量5个协态变量，对应5个状态方程5个协态方程和10个边界条件，另外，式(43)和式(45)分别决定了控制量和飞行时间，构成了一个标准两点边值问题.求解该两点边值问题，得到乘波体最优高宽比:

对应的最佳外形如图3所示，对应的最大航程为13 082 km，最优轨迹曲线如图4～图7所示.

为了验证结果的合理性，固定外形参数ω，分别进行多次单层动态轨迹优化，如图8所示，可见，随着ω的增加，最大航程先是越来越大，后又逐渐变小，即ω存在一个极值点对应全局最大航程.

图3 最优高宽比对应的乘波体外形

图4 外形/轨迹一体优化的最大航程轨迹

图5 外形/轨迹一体优化的速度曲线

图6 外形/轨迹一体优化的控制变量

图7 外形/轨迹一体优化的外形参数协态曲线

图8a中的最优轨迹曲线代表相应的全局最大航程轨迹.

图8b中列出了不同的ω对应的终端航程，最优高宽比 ω*=0.3381.

图8 不同高宽比对应的最大航程轨迹

图8给出了ω=0.05～0.5对应的最大航程轨迹.可见，随着高宽比的增加，乘波体外形由宽短型向细长型发展，对应的最大航程先越来越大，当高宽比超过最优值后又开始变小，这说明高宽比对航程的影响很大，恰当的高宽比能够充分发挥飞行器的潜能.

4 结论

本文给出了一种求解带静态参数最优控制问题的间接法数值算法，并成功地应用在了乘波体的最大航程轨迹优化中.

文中将静态参数分为了3类:终端时间、边界点状态变量和设计变量.针对不同的静态参数，给出了对应的一阶最优必要条件.数值算法结合了直接法和间接法的优点，利用Gauss伪谱方法满足协态映射原理的特点，将Gauss伪谱方法的优化结果作为间接法数值求解器的初始猜测，可以高效而精确地得到最优解，通常只需要数秒钟便可以完成一条弹道的优化计算.以乘波体为研究对象，给出了静态参数外形高宽比的最大航程优化算例，结果显示外形参数对最大航程的影响很大，随着高宽比的增加，乘波体外形由宽短型向细长型发展，对应的最大航程也越来越大，这说明细长型外形具有更好的气动性能，是综合考虑外形和轨迹的优化设计.

References)

［1］ Nan Ying，Chen Shilun，Yan Hui.A common numerical calcula-tion method of optimizing the trajectories of space vehicles［J］.Flight Dynamics，1996，9:20 －26

［2］ Benson D.A Gauss pseudospectral transcription for optimal control［D］.Boston:Massachusetts Institute of Technology，2004

［3］ Huntington G T.Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems［D］.Boston:Massachusetts Institute of Technology，2007

［4］ Yan Hui，Chen Shilu，Nan Ying.Static and dynamic hybrid optimization［J］.AIAA，1997:231 －233

［5］ Hull D G.Optimal control theory for applications［M］.Berlin:Springer-Verlag，2003

［6］ Zhu Xiaolin.Numerical analysis［M］.Heifei:University of Science and Technology of China Press，2010:255 －272

［7］ Shampine L F，Reichelt MW，Kierzenka J.Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c［EB/OL］.http://www.mathworks.com/bvp_tutorial

［8］ Nonweiler T R.Aerodynamic problems of manned space vehicles［J］.Journal of the Royal Aeronautical Society，1959，63(2):521－528

［9］赵志.乘波构型前体的设计与性能计算［D］.西安:西北工业大学，2006 Zhao Zhi.Design and performance calculation of waverider fore body［D］.Xi’an:Northwestern Polytechnical University，2006(in Chinese)

［10］王烁，李萍，陈万春.锥导乘波体气动代理建模方法研究［J］.飞行力学，2012(1):43 －47 Wang Shuo，Li Ping，Chen Wanchun.Reserch on the surrogate of model aerodynamic performance of cone derived waverider［J］.Flight Dynamics，2012(1):43 － 47(in Chinese)

［11］高建力.高超声速飞行器气动特性估算与分析［D］.西安:西北工业大学，2007 Gao Jianli.Estimating and analyzing of aerodynamic of hypersonic vehicle［D］.Xi’an:Northwestern Polytechnical University，2007(in Chinese)

［12］王振国，陈小前，罗文彩，等.飞行器多学科设计优化理论与应用研究［M］.北京:国防工业出版社，2006 Wang Zhenguo，Chen Xiaoqian，Luo Wencai.Research on the theory and application of multidisciplinary design optimization of flight vehicles［M］.Beijing:National Defense Industry Press，2006(in Chinese)