目标威胁规避约束下战斗机引导控制优化方法
2014-03-19付昭旺李战武
于 雷 付昭旺 李战武 李 飞
(空军工程大学 航空航天工程学院,西安 710038)
信息、机动和火力是空战对抗的3个核心要素,由于战斗机攻击范围有限,机动成为战斗机实施火力打击的必要环节,战斗机引导方法成为影响空战效能的重要因素,各种引导方法在空战中得到广泛应用.战斗机经典引导方法主要有追踪法[1]、平行接近法[2]和比例引导及其改进算法[3-4]等,这些引导方法在理论上已趋于成熟,但其引导原理和实际应用都存在不同程度的缺陷[5].为此,一些学者把最优控制理论应用到引导问题中,产生了各种各样的最优引导方法[6-9].但是,目前研究的最优引导方法仅以接近敌方目标为主要目的,大部分情况把目标作为一个运动的飞行器来分析,较少涉及目标的作战能力和威胁.在实际作战中,在我方战斗机向目标引导的同时,目标很可能也在被引导向我方战机,并伺机攻击,且现代空战武器装备都具有强大的超视距攻击能力,不考虑目标威胁的引导不仅非常危险,也不符合现代空战对抗的作战需求.
基于此,根据战斗机引导的安全性约束,提出一种目标威胁规避约束下的战斗机引导控制方法,以空战态势参数为状态建立引导模型,将战斗机引导问题建模为终端时刻未知的最优控制问题,将威胁规避约束转化为引导状态约束,并引入滚动时域控制策略进行在线优化,采用数值解法对最优控制模型进行求解.
1 基于态势参数的战斗机引导模型
在选定的“北-天-东”地理坐标系的战斗机A三自由度运动模型:
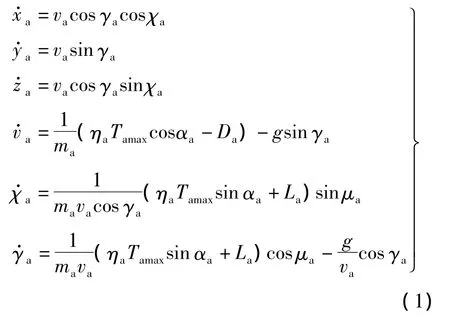
式中,(xa,ya,za)为战斗机的位置坐标;其余状态变量为速度 va、航迹偏航角 χa和航迹倾角 γa;Tamax为飞机当前高度和速度下飞机发动机的最大推力,并假设推力方向通过飞机重心且与飞机纵轴重合;飞机的控制量分别为攻角αa、横滚角μa和推力系数ηa;ma为战斗机质量;g为重力加速度;La为在气流作用下飞机机翼产生的升力,其垂直于飞机纵轴向上;Da为飞机受到的阻力.
同样,以选定的“北-天-东”地理坐标系为惯性坐标系,目标T的运动方程可表示为
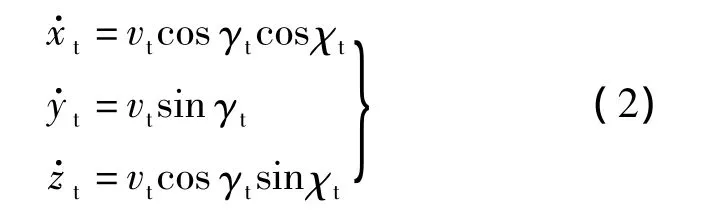
式中,(xt,yt,zt)为目标位置;目标飞行状态参数分别表示为速度vt、航迹偏航角χt和航迹倾角γt.目标位置及其航迹参数由网络中心通过数据链传递给战斗机.
T与A的相对运动模型可表示为
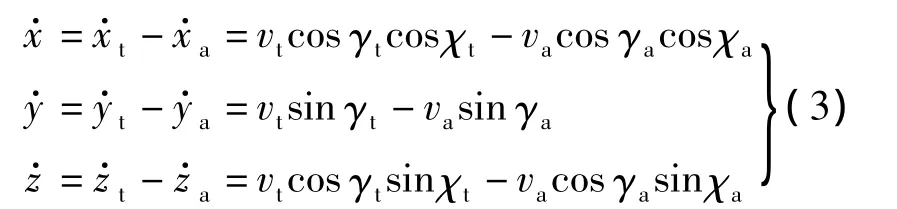
为描述引导过程的空战态势,将式(3)变换到以A为原点的球面坐标系中,并采用目标距离r、目标方位角u、目标俯仰角υ、目标高差h、目标水平进入角q来描述A和T的相对运动状态,规定h以目标在上为正;规定u和q以相对于目标线逆时针方向为正;υ以目标在上为正;则有-π≤u≤π,0≤q≤2π,-π/2≤υ≤π/2.
根据理论力学的运动学关系有
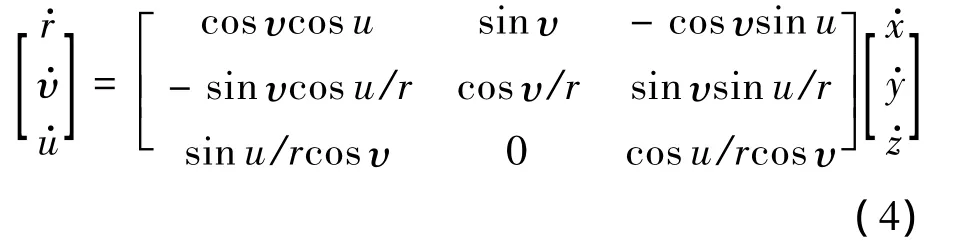
根据目标水平进入角的定义:
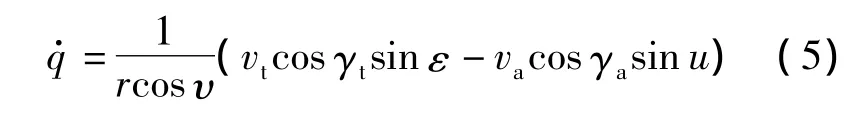
根据目标高差的定义:
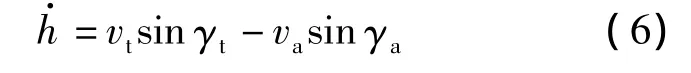

式中,u=[αa,μa,ηa]T为引导的控制向量.
2 目标火力威胁建模
为便于描述,将战斗机引导的目标认为是自身具有攻击能力的战斗机,并以机载空空导弹作为目标的火力威胁源进行建模.空空导弹对目标的攻击距离主要与导弹性能、空战态势和目标特性有关.为此,本文引入武器包线函数[10]来描述机载空空导弹的威胁能力,并以机载空空导弹的有效攻击距离Rm为威胁评估指标:
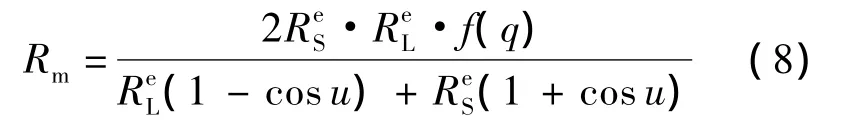
考虑到正迎头攻击即q=0时,导弹对目标具有最大的攻击距离Rf,尾后攻击即q=π时,导弹对目标具有最小的攻击距离Rt,给出f(q):
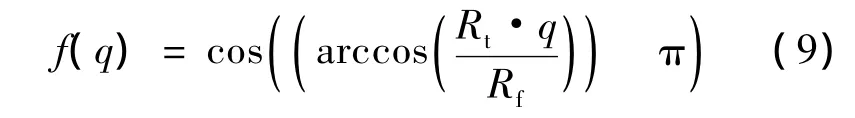
式中,q∈[0,π];Rf和Rt根据导弹的性能参数获得,可以看出,f(q)为单调递减函数,能够反映目标进入角对导弹攻击距离的影响.
式(8)描述了战斗机在水平面内的攻击包络.考虑到导弹攻击时高差的影响,对式(8)进行高差修正,为简便计算,假设导弹的上视和下视最大允许攻击高差相同,考虑到导弹的下射攻击具有能量优势,导弹的下射攻击距离一般大于上射攻击距离.因此,给出高差修正因子:
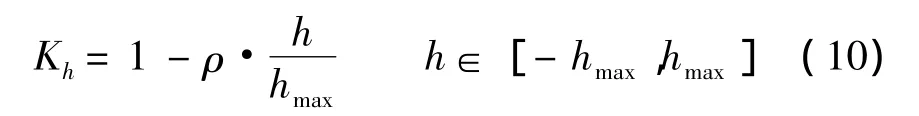
式中,h以目标在上为正;ρ取为导弹在标准高度以最大高差发射时射程增大的百分比;hmax>0为导弹最大允许攻击高差.可以看出,下视攻击时,Kh随着h增大而增大,上视攻击时,Kh随着h增大而减小,该公式能够有效反映高差对导弹攻击距离的影响.
基于上述分析,综合考虑导弹性能和空战态势下机载导弹的有效攻击距离为

现代空空导弹具有全向攻击能力,但考虑到导弹攻击的信息需求,导弹攻击范围受到目标探测能力约束,因此,取 u ∈(- ψmax,ψmax),ψmax> 0表示战斗机机载传感器的最大探测方位角.
3 引导的最优控制模型
3.1 问题描述
战斗机引导控制优化问题可建模为如下终端时刻自由的最优控制问题:
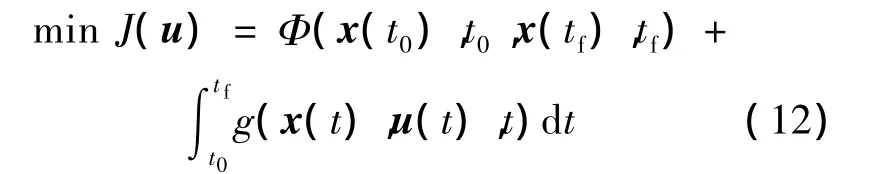
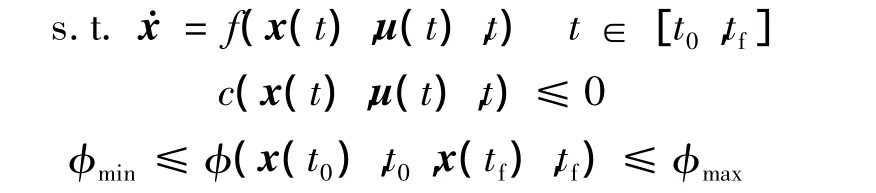
3.2 状态方程的无量纲化
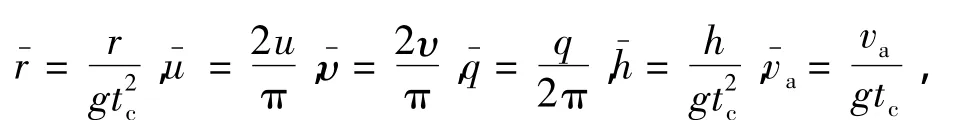
3.3 性能指标函数
性能指标的选取首先应考虑引导的快速性,为保证引导效果,同时应考虑引导控制的可操作性.快速性指标采用最小化引导时间进行约束:
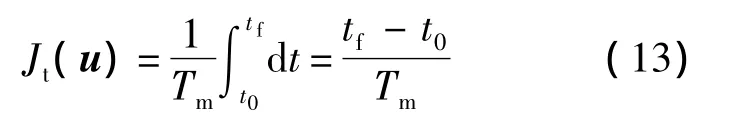
式中,Tm为最大可用时间;其余变量定义同上.
可操作性可以通过引导的控制损耗进行约束,以载机旋转角速度来构建控制损耗的指标函数:
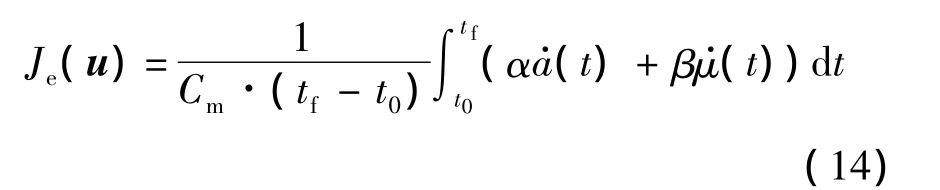
式中,Cm为最大可用控制损耗和)分别为横向加速度和滚转角速度;α,β为加权因子.
综合考虑上述指标,给出如下指标函数:
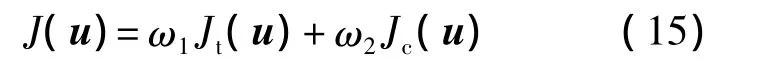
式中ωi(i=1,2)为指标加权因子,用于调节快速性和经济性的指标权重.
3.4 引导控制约束分析
3.4.1 威胁规避约束
为保证引导的安全性,应严格控制战斗机的接敌态势,根据式(7)所示的引导模型,可将引导的态势约束进一步转化为对引导状态的约束,以SA表示目标火力威胁范围,威胁规避下的空战态势约束可以表示为图1所示.
威胁规避约束可表示为
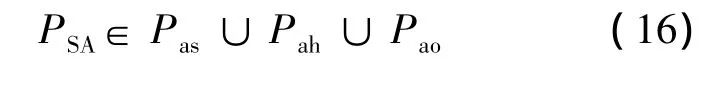
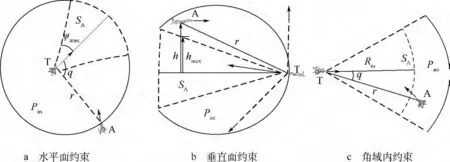
图1 火力威胁规避下的态势约束
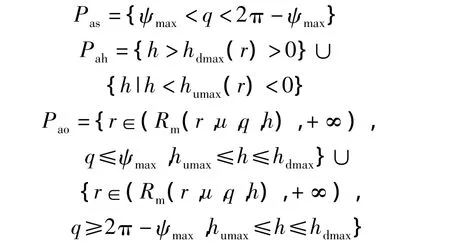
式中,Pas表示A位于T水平探测范围外;Pah表示A位于T的攻击高差外;Pao表示A位于T的可探测角域内,但A与T的距离大于T的有效攻击距离,其中 Rm(r,u,q,h)的计算方法见式(11).
3.4.2 控制量约束
为保证控制的有效性,需对控制量进行约束:
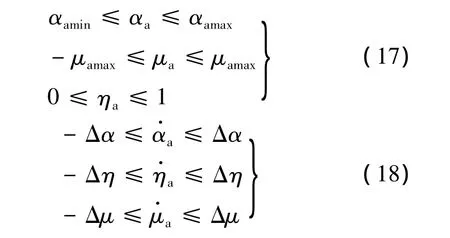
式中,αamin和αamax分别为飞机的最小、最大攻角;μamax为飞机的最大滚转角;Δα,Δμ和Δη分别为攻角、滚转角和油门位置的最大变化率.
3.4.3 终端约束
引导的目的是实现武器发射,因此,将终端约束取为A达成导弹发射的边界条件:
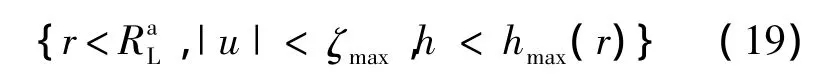
4 滚动时域控制及其数值解法
4.1 滚动时域控制方法
为保证引导控制模型求解的实时性,引入滚动时域控制(RHC,Receding Horizon Control)[11]策略进行滚动优化,RHC实现方法如图2所示.
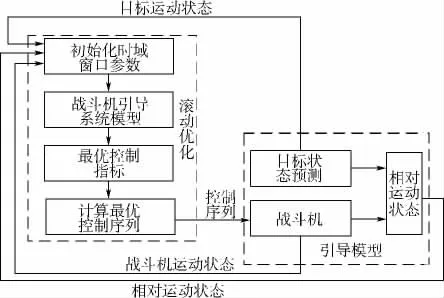
图2 引导控制的RHC方法
RHC中,选择合适的性能指标函数非常关键.由于引导控制的终端时刻是未知的,但是在规划时域t∈[tk,tk+T]内,剩余飞行时间可通过双方接近速度估计得出,记Vr=r·为双方接近速度,对于引导的快速性,指标函数可取为剩余的引导时间最短:
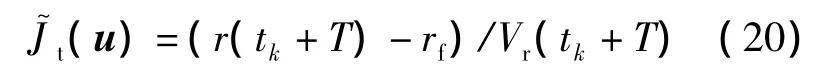
对于引导的经济性,指标函数选取为剩余时间内战斗机的累积控制损耗最小:
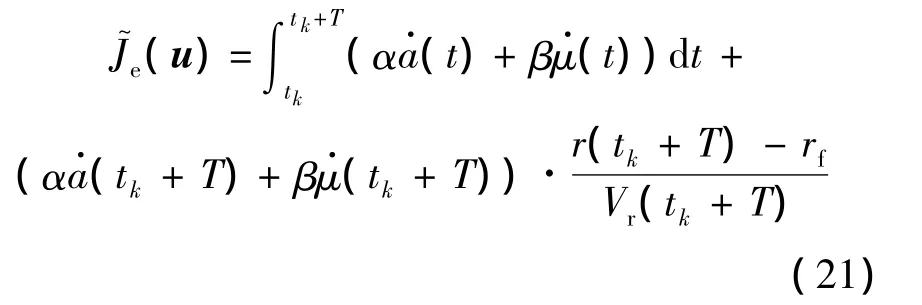
则在每一个滚动时域内,指标函数取为
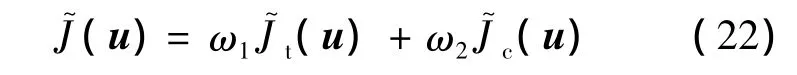
4.2 基于高斯伪谱法的数值求解
引导控制模型是非线性的,难以通过解析法获得最优解,需要采用数值解法进行求解.高斯伪谱法(GPM,Gauss Pseudospectral Method)[12]是解决非线性最优控制问题的一种高效的数值解法.采用GPM进行模型离散化,可将连续的最优控制问题转化为离散的NLP(Non-Linear Programming)问题.
采用GPM可以将式(12)所示的最优控制问题转换为如下离散形式[13]:
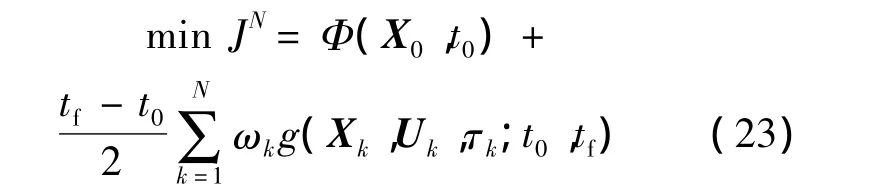
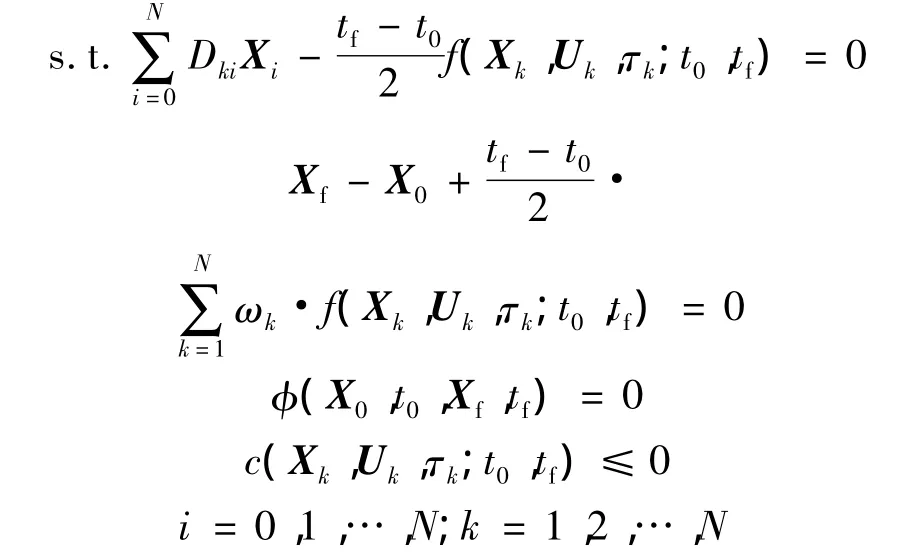
式中,第1项为系统状态约束;第2项为终端状态约束;φ(X0,t0,Xf,tf)=0 为边界条件;c(Xk,Uk,τk;t0,tf)≤0为威胁约束.通过采用GPM进行模型离散化,最优控制问题转化为寻找Xk,Uk(k=1,2,…,N)和 tf,使得性能指标 J 取得极小值,并满足原最优控制问题约束的NLP问题,可以采用序列二次规划(SQP,Sequential Quadratic Programming)[14]等多种算法进行求解.
5 仿真分析
为验证引导控制方法的有效性,给定战场想定进行仿真.假设战斗机A在预警机的信息支援下向目标T进行引导.A的航空动力学参数取自F-16A的简化模型[15],目标T的机载武器性能设置见表1.

表1 目标T的武器性能参数
仿真步长d t取为1 s.为了充分验证引导模型的威胁规避能力,假设在引导过程中,T采用平行接近法向A进行导引,而A根据文中的引导模型获取引导控制指令,RHC时域窗口取为T=4s.控制损耗指标取α=0.4和β=0.6,A和T的初始态势如表2所示,A的初始状态参数如表3所示.
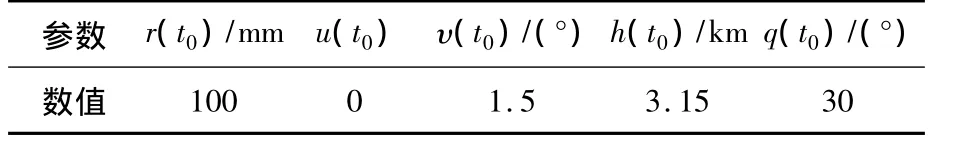
表2 A和T的初始态势

表3 A的初始状态
引导终端约束设为:r(tf)≤30km,|u(tf)|≤30°,h(tf)≤ 0 ,性能指标权重取为 ω1=0.75,ω2=0.25.在 Matlab 环境下采用 GPOPS(Version 2.3)软件包[16]进行仿真,GPOPS 内集成了 GPM 和NLP的求解方法.仿真结果如图3~图6所示,图中参数含义与式(7)相同.
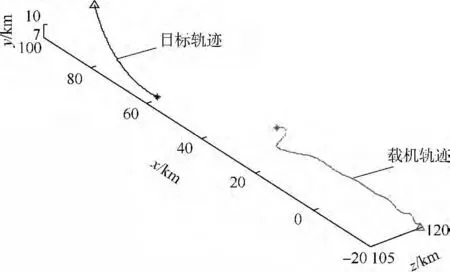
图3 A与T的运动轨迹
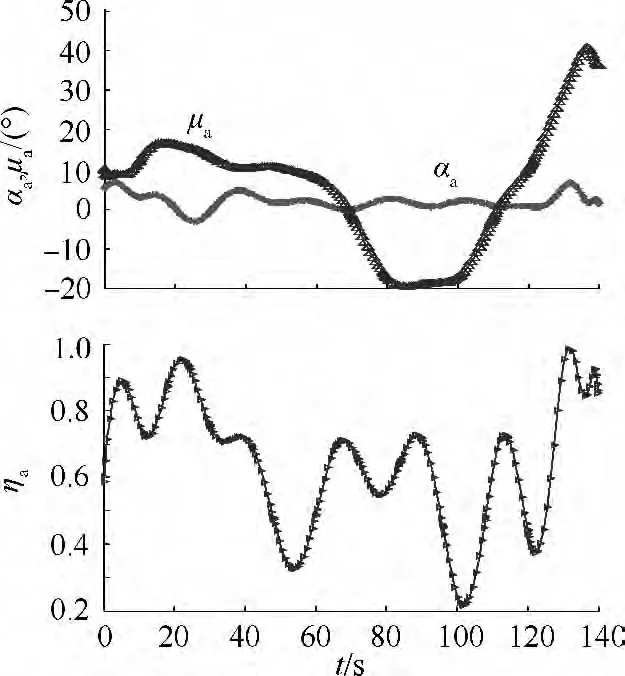
图4 战斗机引导的控制量
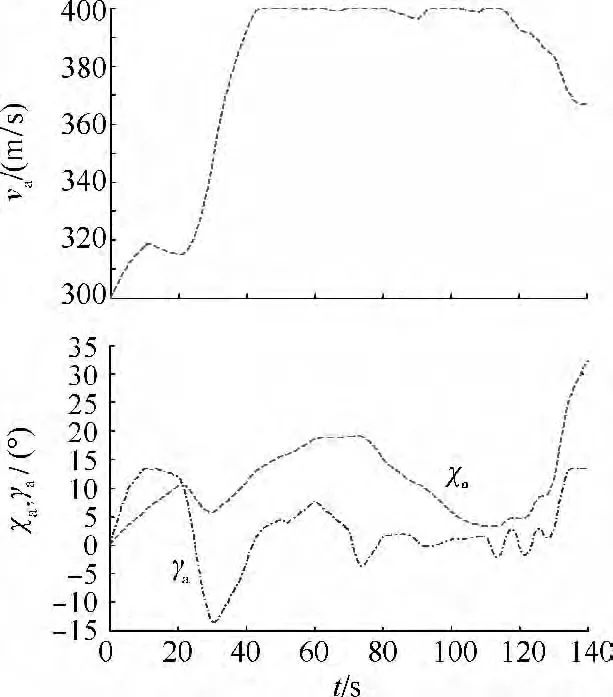
图5 A的飞行状态变化
由图5中va和图6中r的曲线可以看出,在引导起始,战斗机迅速加速,并持续保持最大速度向目标引导,而在引导后段进行了减速机动.由图6中q和u的曲线可知,目标方位角和目标进入角随相对距离减小而增大,这是由于A通过侧向机动增大目标进入角能压缩目标的导弹有效攻击距离,以此来规避目标火力威胁.从图4和图5可以看出,优化的引导控制量和A的飞行状态变化都比较平稳,说明优化的轨迹具有良好的可飞性.仿真得到引导终端的状态为:r(tf)=29.9 km,u(tf)=-26.2°,h(tf)=-68m,表明战斗机达成了给定的终端状态.
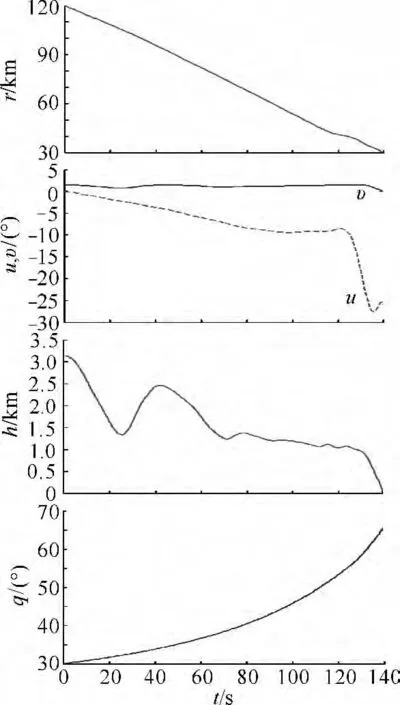
图6 A与T的态势参数变化
为分析算法的实时性,使主程序在通用Pentium 4 2.0GHz,1GB内存的微型计算机平台上运行,结果表明,基于RHC策略在线优化的单次计算时间小于0.1 s,表明引导算法能满足空战引导的实时性需求.
6 结论
威胁规避是空战引导的重要内容,也是实现空战精确打击的重要前提.本文对威胁规避约束下的战斗机引导控制方法进行了研究,仿真结果表明,所提出的引导方法能在保证引导安全性的前提下实现战斗机的最优引导.采用威胁规避引导能有效增强战斗机引导的安全性,提高战斗机攻击效能.同时,该引导控制方法也非常适合推广应用于无人战斗机自主攻击的引导控制,对于无人机空战应用具有一定的参考价值.
References)
[1]强胜,龙汉,申镇,等.追踪法推广的数学建模与仿真[J].兵工学报,2009,30(1):56 -62 Qiang Sheng,Long Han,Shen Zhen,et al.Generalized mathematical model and simulations of pursuit guidance method[J].Acta Armamentarii,2009,30(1):56 -62(in Chinese)
[2]赵文成,那岚,金学英.准平行接近法导引律的研究与实现[J].测控技术,2009,28(3):92 -95 Zhao Wencheng,Na Lan,Jin Xueying.Research and realization of quasi-parallel approaching method[J].Observation and Control Technology,2009,28(3):92 -95(in Chinese)
[3]王辉,林德福,祁载康.时变最优的增强型比例导引及其脱靶量解析解[J].红外与激光工程,2013,42(3):692 -698 Wang Hui,Lin Defu,Qi Zaikang.Time-varying optimal augmented proportional navigation and miss distance closed-formed solution[J].Infrared and Laser Engineering.2013,42(3):692 -698(in Chinese)
[4] Tyan F,Shen JF.A simple adaptive GIPN missile guidance law[C]//Proceedings of the 2006 American Control Conference.Minneapolis,Minnesota,USA:IEEE,2006:345 -350
[5]周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002 Zhou Di.New guidance law for homing missile[M].Beijing:National Defense Press,2002(in Chinese)
[6]冯艳清,周红丽,程凤舟,等.带末端攻击角度约束的三维最优导引律研究[J].战术导弹技术,2011(5):81-85 Feng Yanqing,Zhou Hongli,Cheng Fengzhou,et al.Study of three-dimensional optimal guidance law with terminal constraints[J].Tactical Missile Technology,2011(5):81 - 85(in Chinese)
[7] Rusnak I.Optimal guidance laws with uncertain time-of-flight against maneuvering target and noisy measurements[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Austin,Texas:AIAA,2003:5576-1 -5576-8
[8] Ryoo C K,Cho H,Tahk M J.Time-to-go weighted optimal guidance with impact angle constraints[J].IEEE Transactions on Control Systems Technology,2006,14(3):483 -492
[9] Wang Zhigang,LiWei.Three dimensional optimal guidance law for micro missiles to attack maneuvering targets[J].Informatics in Control,Automation and Robotics,2012,133(5):283 - 286
[10] Menon P K A,Duke E L.Time-optimal aircraft pursuit evasion with a weapon envelope constraint[J].Journal of Guidance Control and Dynamics,1992,15(2):448 -456
[11] Zhan ZH,Zhang J,Li Y.An efficient ant colony system based on receding horizon control for the aircraft arrival sequencing and scheduling problem[J].IEEE Transactions on Intelligent Transportation Systems,2010,11(2):399 -412
[12]唐国金,罗亚中,雍恩米.航天器轨迹优化理论、方法及应用[M].北京:科学出版社,2012 Tang Guojin,Luo Yazhong,Yong Enmi.Theory,method and application of trajectory optimization for spacecraft[M].Beijing:Science Press,2012(in Chinese)
[13] Huntington G T,Benson D,Anil V R.A comparison of accuracy and computational efficiency of three pseudospectral method[J].AIAA Guidance,Navigation and Control Conference and Exhibit South Carolina,2007:6405 -6429
[14] Dua V,Bozinis N A,Pistikopoulos EN.A multi-parametric programming approach for mixed-integer quadratic engineering problems[J].Computer and Chemical Engineering,2002,26(4):715-733
[15] Horie K,Conway B A.Optimal fighter pursuit-evasion maneuvers found via two-sided optimization[J].Journal of Guidance,Control,and Dynamics,2006,29(1):105 -112
[16] Gill P E,Murray W,Saunders M A.SNOPT:an SQP algorithm for large-scale constrained optimization[J].SIAM Journal on Optimization,2002,12(4):979 -1006
