测量不确定度的评定在检测实验室的应用
2014-03-18沈文馨
沈文馨
(江西省分析测试研究所,江西 南昌 330029)
1 引言
随着实验室认可体系和质量认证体系在我国推行,测量不确定度越来越引起实验室的重视。《检测和校准实验室认可准则》和GB/T27025-2008《检测和校准实验室能力的通用要求》对实验室不确定度评定作了明确的要求。首先,在出具检验报告时,实验室要对检测结果的可靠性进行评定。第二,实验室外送检测仪器检定/校准时,如果所获得的证书是校准证书,应根据校准证书所提供的技术参数进行技术确定,要应用到测量不确定度。第三,实验室在进行内部质量控制时要应用测量不确定度。第四,实验室在进行期间核查时也要应用测量不确定度。
2 基本概念
2.1 测量不确定度的概念
测量不确定度实质上就是对真值所处范围的评定,也是对测量误差可能大小的评定,也是对测量结果不能肯定的程度的评定,三种说法都是一样的,没有本质的区别。而这种评定必须与测量相联系。必须有可操作性,于是新的定义为:表征合理地赋予被测量之值的分散性,与测量结果相联系的参数。
2.2 标准不确定度(u)
以标准偏差表示的测量不确定度。
2.3 合成标准不确定度(uc)
当测量结果是由若干个其他量的值求得时,按方差或(和)协方差算得的标准不确定度。
2.4 扩展不确定度(U)
确定测量结果区间的量,合理赋予被测量之值分布的大部分可望含于此区间,它可用合成不确定度乘以包含因子U=k·uc。
2.5 相对不确定度
有时为了计算方便和结果比较而采用相对不确定度:一个量的不确定度除以该量的平均值,加以脚标rel(relative)表示。
2.6 A类不确定度(ucA)
用对观测列进行统计分析的方法来评定标准不确定度。
2.7B类不确定度(ucB)
用不同于对观测列进行统计分析的方法来评定标准不确定度。
2.8 包含因子(k、kp)
为获得扩展不确定度所乘的数字因子。


2.9 自由度
反映了相应标准不确定度的可靠程度,它用来评定不确定度质量。
2.10 相关系数
是两个变量之间相互依赖性度量,它等于两个变量间的协方差除之各自方差之积的正平方根。对检测实验室一般可以不考虑相关性。
2.11 灵敏系数

3 测量不确定度来源
3.1 被测量的定义不完整或不完善;
3.2 测量方法不理想;
3.3 取样的代表性不够,即被测样本不能完全代表所定义的被测量;
3.4 对测量过程受环境影响的认识不周全,或对环境参数的测量与控制不完善;
3.5 读数误差的影响;
3.6 仪器设备的性能不佳;
3.7 测量标准或标准物质的不确定度;
3.8 引用的数据或其他参数的不确定度;
3.9 在相同条件下被测量在重复观测中的变化。
4 测量不确定度评定方法
4.1 标准不确定度A类评定。
对被测量x,在重复条件下或复现条件下进行n次独立重复观测,观测值为xi(i=1,2,3…,n)。

S(xi)为单次测量的实验标准差,由贝塞尔公式得:
式中xi:第i次测量的结果;
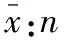
υi:残差。
根据定义,以标准偏差表示的测量不确定度为标准测量不确定度,对应的A类评定标准不确定度u(x)为:

4.2 标准不确定度B类评定。
4.2.1 B类标准不确定度信息来源。
4.2.1.1 理论分析。
4.2.1.2 证书、手册、技术说明书、资料提供。
4.2.1.3 经验。
4.2.1.4 权威部门、权威人士评定。

用这类方法得到的估计方差u2(xi),可称为B类方差。u(xi)即为B类标准差。
4.2.2 不同信息的B类标准差。
4.2.2.1 已知扩展不确定度U和包含因子k,
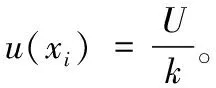
4.2.2.2 已知扩展不确定度Up

正态分布中的p%和kp关系见下表。

表2-4 正态分布中的p%与kp关系
4.2.2.3 已知扩展不确定度Up和置信概率及有效自由度νeff的t分布,

需查t分布表得tp(νeff),再据上式求u(xi)。
以上三种情况中的U和Up可以从校准证书中得到。
4.2.2.4 已知置信区间半宽度a和对应于置信概率的包含因子k,

4.2.2.5 其它几种分布:
除t分布外,还有均匀,三角,反正弦,梯形,两点等分布,已知半宽度为a,且±a区间内概率p=100%。
4.2.2.6 已知重复性限r或复现性限R求u(xi)
u(xi)=r/2.83u(xi)=R/2.83
(r、R置信水平95%,正态)
4.2.2.7 以“等”使用仪器的u(xi)。
4.2.2.7.1 当证书上给出准确度等别时,可按检定系统表或检定规程所规定的扩展不确定度U(xi)或Up和k或kp值。

4.2.2.7.2 可找出Up、p与νeff时,按t分布处理

4.2.2.8 以“级”使用仪器的u(xi)
当证书上给出准确度级别时,可按检定系统或检定规程所规定的最大允许误差±A
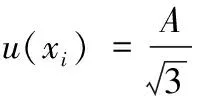
4.3 合成标准不确定度的评定
对于检测实验室,在评定合成标准不确定度时,可以认为各输入量xi彼此独立不相关,则合成标准不确定度为:
检测实验室的测量中,往往假设各影响量的不确定度分量对测量结果的灵敏程度相同,设灵敏系数ci为1。合成标准不确定度可简化表示为:
uc(y)——合成标准不确定度,也可写为uc;
ui=u(xi)——各输入量的标准不确定度;
ciui——标准不确定度的分量;
uc(y)——合成标准不确定度,可写为uc;
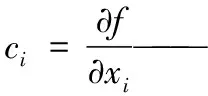
4.4 扩展不确定度的评定
合成标准不确定度属于标准不确定度,是建立在标准不确定度的基础上的(各分量都是标准不确定度)。而用标准不确定度给出测量结果所在的区间,只是被测量值可能出现的一部分(如正态分布只占68.27%),其可信程度(用置信概率定量表示)不高,为了提高对测量结果所在区间评定的可信程度,需加以扩展。
4.4.1 在合成不确定度uc(y)确定后,要乘以包含因子k,则k=2~3。y接近正态分布,νeff有效自由度较大时,一般取k=2。
4.4.2 如果uc(y)的自由度较小、并要求区间具有规定的置信水准p、则kp采用t分布临界值,即kp=tp(νeff)——简称t值,从查t分布表得到。一般p值为99%和95%,多数情况采用p=95%。
4.4.3y不是正态分布,则要根据其它的分布曲线计算。
对矩形k95=1.65,k99=1.71;
对三角分布k95=1.90,k99=2.20;
对正态分布k95=1.96,k99=2.58。
5 报告与表示
报告通常以合成标准不确定度和扩展不确定度的形式来表示。
5.1 测量结果及其合成标准不确定度的报告,可用以下三种方式表示:
例如:标准砝码的质量为ms,测量结果为100.02147g,合成标准不确定度uc(ms)为0.35mg,则报告形式有:
5.1.1 ms=100.02147g;uc(ms)=0.35mg。
5.1.2 ms=100.02147(35)g;括号内的数是合成标准不确定度,其末位与前面结果的末位数对齐。这种形式主要在公布常数或常量时使用。
5.1.3 ms=100.02147(0.00035)g;括号内的数是合成标准不确定度,与前面结果有相同的测量单位。
5.2 扩展不确定度的报告可以有U、Up和Urel三种方式表示:
5.2.1U=uc(y)的报告。
例如:标准砝码的质量为ms,测量结果为100.02147g,合成标准不确定度uc(ms)为0.35mg,取包含因子k=2,U=uc(y)=2×0.35mg=0.70mg。U可用以下两种形式之一报告:
5.2.1.1 ms=100.02147g;U=0.70mg;k=2。
5.2.1.2 ms=(100.02147±0.00070)g;k=2。
5.2.2Up=kpuc(y)的报告。
例如:标准砝码的质量为ms,测量结果为100.02147g,合成标准不确定度uc(ms)为0.35mg,νeff=9,p=95%,查表得kp=t95(9)=2.26,U95=2.26×0.35=0.79mg,则Up可用以下四种形式之一报告:
5.2.2.1 ms=100.02147;U95=0.79mg,νeff=9。
5.2.2.2 ms=(100.02147±0.00079)g;νeff=9,括号内的第二项为U95的值。
5.2.2.3 ms=100.02147(79)g;νeff=9,括号内为U95的值,其末位与前面结果的末位数对齐。
5.2.2.4 ms=100.02147(0.00079)g;νeff=9,括号内为U95的值,与前面结果有相同的测量单位。
5.2.3 以相对形式Urel报告。
5.2.3.1 ms=100.02147(1±7.9×10-6)g;p=95,式中7.9×10-6为U95rel值。
5.2.3.2 ms=100.02147g;U95rel=7.9×10-6。
5.3 不确定度数值
不确定度数值最多取2位,计算过程中可取2-3位。测量结果的有效位数应与其不确定度相匹配,不可过多,以免引起对测量精确程度的误解。
6 测量不确定度评定实例

6.1 数学模型
式中:c—标准溶液浓度;
m—高纯金属银质量(mg);
p—金属银纯度;
v—标准溶液体积(L)。
6.2 求标准不确定度分量urel(m)(银质量对不确定度的贡献分量)
称量样品的不确定度来自三个方面:第一,称量的重复性,可以通过10次重复测量,采用A类评定方法求出;第二,由天平称量不准引入的不确定度,有电子天平的最大允许误差,按B类方法评定;第三,天平标度的可读性(数字分辨力),按B类方法评定。由上面三方面评估的合成标准不确定度为0.035mg,由于在称量标准物质银的量时,是采用二次称量得出的,即由一次回零(空瓶)称量所得,质量m标准不确定度为:
采用相对标准不确定度表示:
6.3 求标准不确定度分量urel(p)(银纯度对不确定度的贡献分量)
6.4 求标准不确定度分量urel(v)(标准溶液体积对不确定度的贡献分量)
6.4.1 校准影响(玻璃仪器容量对体系不确定度的贡献分量)
6.4.2 重复性(人员操作重复性对体积不确定度的贡献分量)
对典型的100mL容积瓶重复充满10次,得出单次的标准偏差为0.02mL。
6.4.3 温度变化的影响(温度变化对体积不确定度的贡献分量)
6.4.4 体积对不确定度的贡献合成
6.5 求合成标准不确定度
uc=C×urel(C)=1001.7×0.0009=0.9mg/L
6.6 求扩展不确定度
取k=2
U=kuc=2×0.9=1.8mg/L
6.7 测量结果

7 讨论
检测实验室通过对测量不确定度的来源分析,对影响检测结果的因素加以控制,并建立相关程序文件,保证检测工作严格按照规范进行。通过分析不确定度,把检测误差控制在容许范围,使检测数据在给定的置信水平内,确保检测结果的准确可靠。开展好测量不确定度的评定,是实验室提高检验结果可靠性的重要保障,是实验室检测水平高低的体现。
[1]国家质量技术监督总局.测量不确定度评定与表示[M].北京:中国计量出版社,1999.
[2]GB/T27025-2008,《检测和校准实验室能力的通用要求》[S].
[3]中国合格评定国家认可委员会.测量不确定度要求的实施指南[Z].2011.
[4]中国实验室国家认可委员会.实验室认可与管理基础知识[M].北京:中国计量出版社,2003.
